空气弹簧高度振荡自适应模糊PID控制方法研究
李子璇 ,邬明宇,周福强,危银涛
(1.北京信息科技大学现代测控技术教育部重点实验室,北京 100192;2.清华大学汽车安全与节能国家重点实验室,北京 100084)
0 前言
空气悬架近年来受到了广泛的关注,其控制性能的好坏直接影响着车辆行驶过程中的平顺性、操纵性及稳定性。空气弹簧利用气体的可压缩性实现弹性作用,根据车辆行驶状况和路面的工况实现悬架的刚度和高度的调节,从而提高车辆乘坐的舒适性。
空气弹簧的高度振荡控制需要满足响应速度快、控制精度高等特性。GAO等运用静态车辆高度调整平衡位置状态观测算法,提出模糊逻辑控制策略。江洪、PRABU等提出了PID控制策略。KIM 和LEE运用滑模自适应控制技术对空气悬架车身高度进行了控制,并对系统进行了仿真。徐兴等人分析了振荡现象的形成机制,提出了变速积分PID/PWM高度控制策略。MA、SUN等对整车进行模型预测控制。CHEN等提出线性二次最优控制。这些控制方法都取得了较好的效果,但控制系统有时比较复杂,不利于在实际中应用。模糊控制的优点是鲁棒性好、容错性强,缺点是具有稳态误差;PID控制的优点是可以消除稳态误差,将模糊控制与PID控制相结合可以很好地将两种控制方法的优点结合起来,使控制效果得到提升。
结合上述控制策略,提出将自适应模糊PID运用到热力学建模的空簧系统上,设计车身高度模糊PID控制器,并通过MATLAB/Simulink联合仿真分析模糊PID控制器的控制性能,与单纯的PID控制相比较,模糊PID控制策略具有更加稳定的控制效果。
1 空气悬架仿真模型的建模
1.1 空气悬架气路系统原理
空气悬架系统通过对空气弹簧的充、放气调节车身的高度。充放气气路结构如图1所示,主要包括空气弹簧、空气压缩机、电磁控制阀、蓄压器等。

图1 空气弹簧充放气气路结构
空气弹簧的充放气是一个封闭的过程,可以通过电磁阀实现充放气过程中气路的切换。当车身需要升高时,对空气弹簧进行充气,蓄压器内的气体通过电磁阀进入空气弹簧中,空气弹簧内的压力增大,簧载位移增大,车身升高;当车身需要降低时,空气弹簧内的气体通过电磁阀进入到蓄压器中,空气弹簧内的压力降低,簧载位移减小,车身降低。
1.2 空气悬架系统建模
1/4车辆二自由度模型基本结构如图2所示,可以较好地反映系统的垂向动力学特性。
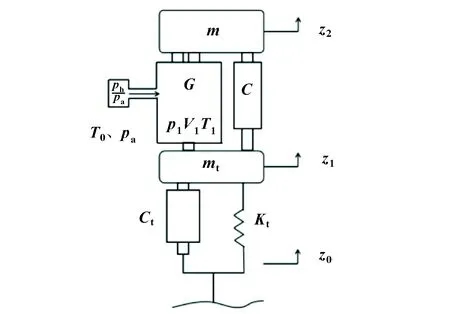
图2 1/4车辆二自由度模型
图2中,为悬挂质量,为非悬挂质量,为减振器阻尼系数,为轮胎的等效阻尼,为轮胎的等效刚度,为外界输入控制体的质量流量,为气室内绝对压力,为大气压,为高压气源气压,为大气温度,为气室内温度,为气室内体积,为悬挂质量位移,为非悬挂质量位移,为路面激励位移。
1.2.1 气路模型建模
热力学分析方法不需要经验或者数据拟合来确定指数,将空簧气室内的气体作为控制体,采用热力学第一定律,就可以清楚地反映出不同的物理过程对应的能量的影响。假设气室内的温度等于气室与管路连接处的温度,可以得到空簧气室模型的微分方程:
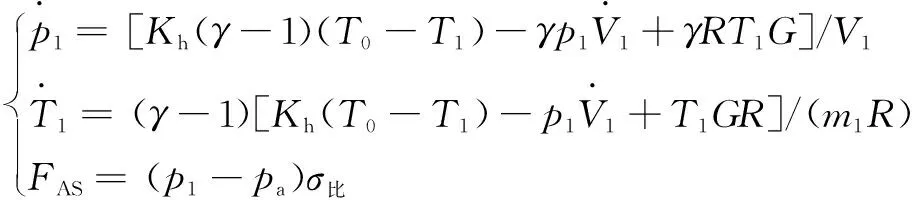
(1)
式中:为气室内质量;为理想气体常数(定压比热容-定容比热容);为气室的导热系数;为空气的比热容比;为外界输入气体的质量流量,即的变化率,充气时为正,放气时为负,无控制指令时为0;为气囊产生的作用力;为空簧气室作用力与气室内相对压力的比值。
气室内体积与有效面积对高度的变化规律可以表示为

(2)
式中:为初始状态下气室的体积;为初始状态下气室的有效面积;为体积随高度的变化率;为有效面积随高度的变化率;(-)为气室高度增加量。
1.2.2 管路模型建模
将连接管路模型等效为一个节流孔,用公式(3)表示为
=(-)
(3)
其中:在文中视作常数。
假设气体充放气过程中,车高调节过程中的温度与大气温度近似,简化动力学模型,结合1/4二自由度车辆模型,可以得到空气悬架的1/4车辆动力学方程为

(4)
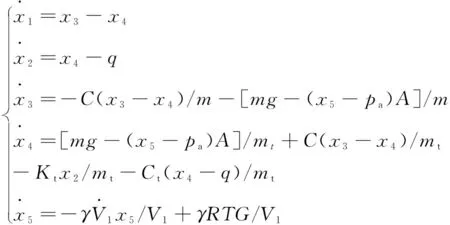
(5)
2 模糊PID控制器的设计
2.1 模糊PID控制原理及结构框图
模糊PID控制系统主要包括模糊控制器、PID控制器、输入/输出接口和被控对象。自适应模糊PID控制器以车身高度偏差和偏差的变化率作为系统的输入,满足不同时刻的和对PID参数的自整定,利用模糊控制规则对PID的参数进行修正。选择二维模糊控制器,系统框图如图3所示。
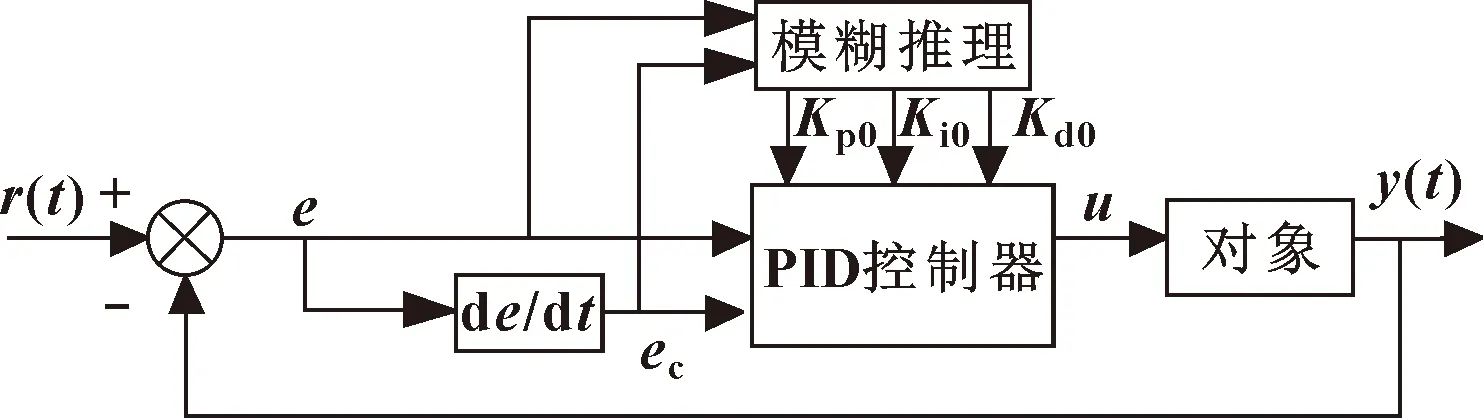
图3 模糊PID控制系统框图
图3中:()为输入设定值函数;()为输出实际值函数;、、为模糊输出变量。
对误差和误差变化率进行模糊推理后可以得到PID控制器3个变量参数的调整量:
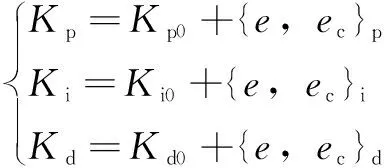
(6)
式中:、、为PID控制器的初始设定值;{,}为不同时刻的车身高度偏差和偏差的变化率对PID的调整函数。
2.2 模糊PID控制器的设计
2.2.1 模糊化处理
设置变量、、、、的论域范围,考虑到车身高度偏差、偏差变化率及控制量的正负性,将偏差、偏差变化率及控制量划分为7个模糊集合{NB(负大), NM(负中),NS(负小),ZO(零),PS(正小),PM(正中),PB(正大)}。选取输入输出的模糊论域均为[-6,6],变量和的基本论域均为[-0.02,0.02],的基本论域为[-2, 2],的基本论域为[-1,1],的基本论域为[-6,6],隶属度函数设为7个,选择三角形函数作为隶属度函数,此隶属度函数可以在误差出现时,迅速反应并做出相应的调整。
2.2.2 模糊控制规则的建立
模糊控制规则的建立是模糊PID控制的核心,模糊规则可以根据当前时刻系统产生的误差,及时做出相应的调整,以确保系统的性能。控制系统的控制规则如下:
(1)当||较小时,为增加系统的稳定性,取较大的和,避免系统出现振荡;当||较小时,取较大的,当||较大时,取较小的;
(2)当||和||都适中时,为减小系统超调,取较小的,为避免过饱和,取较小的;
(3)当||较大时,为加快响应速度,取较大的,为避免过饱和,取较小的,为减小超调量,取较小的;
(4)当和方向一致时,误差会增大,增大可以减小误差,反之,应减小。
、、的模糊控制规则分别如表1—表3所示。
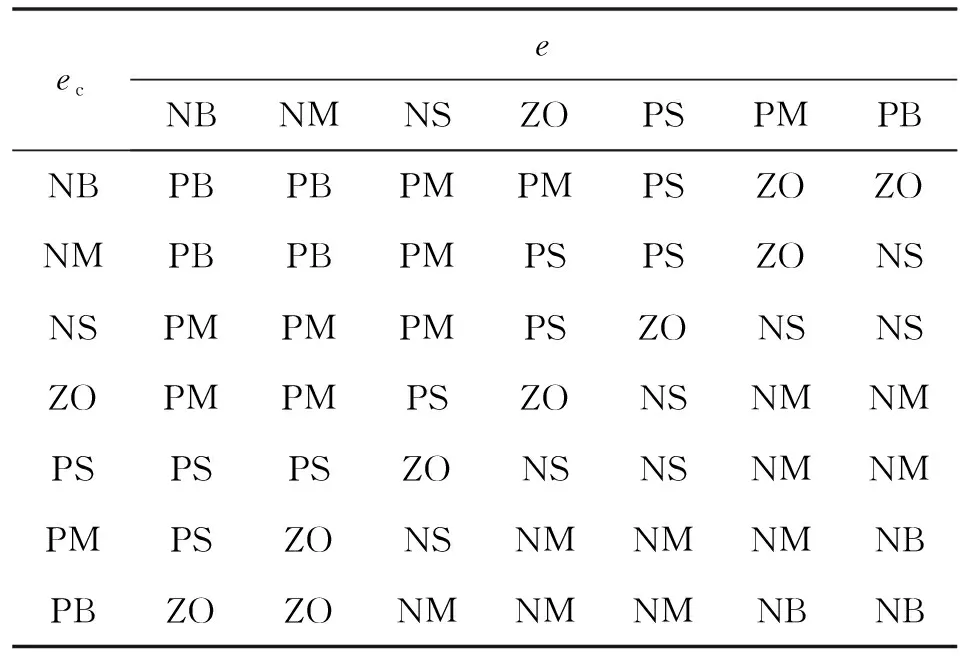
表1 Kp0模糊控制规则

表2 Ki0模糊控制规则
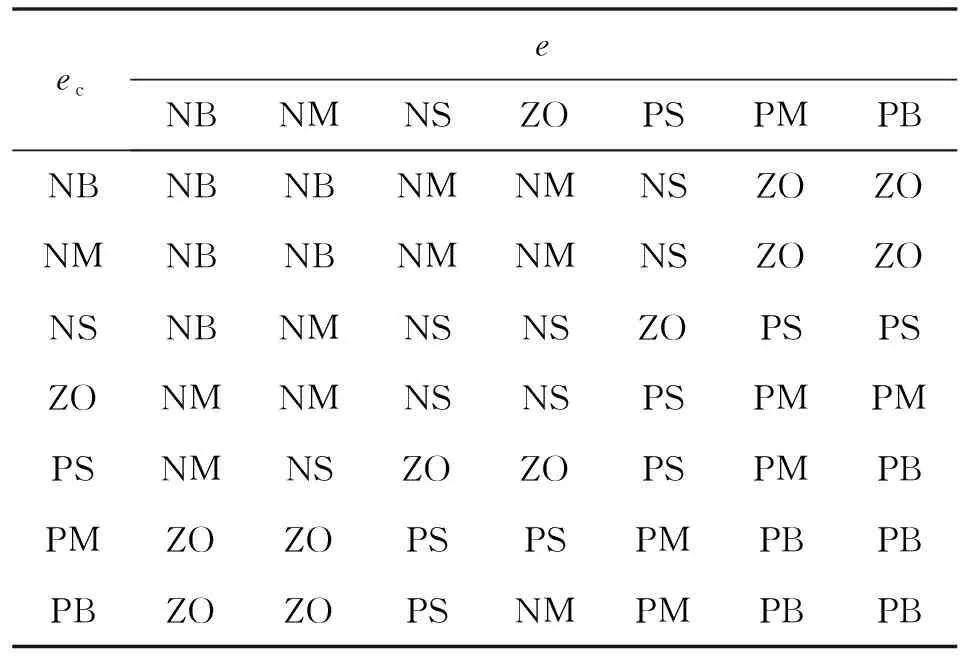
表3 Kd0模糊控制规则
3 MATLAB/Simulink联合仿真与分析
3.1 路面模型的建立
汽车在实际的行驶过程中会受到诸多因素的影响,考虑路面的不平度,车辆行驶过程中受到的路面激励可以用滤波白噪声模拟,其时域数学模型表达式为
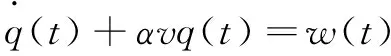
(7)
式中:()为车轮受到的路面随机激励;为空间频率常数;为车辆行驶速度;()为高斯分布白噪声。
假设车辆以50 km/h的速度通过B级路面,其仿真激励曲线如图4所示。
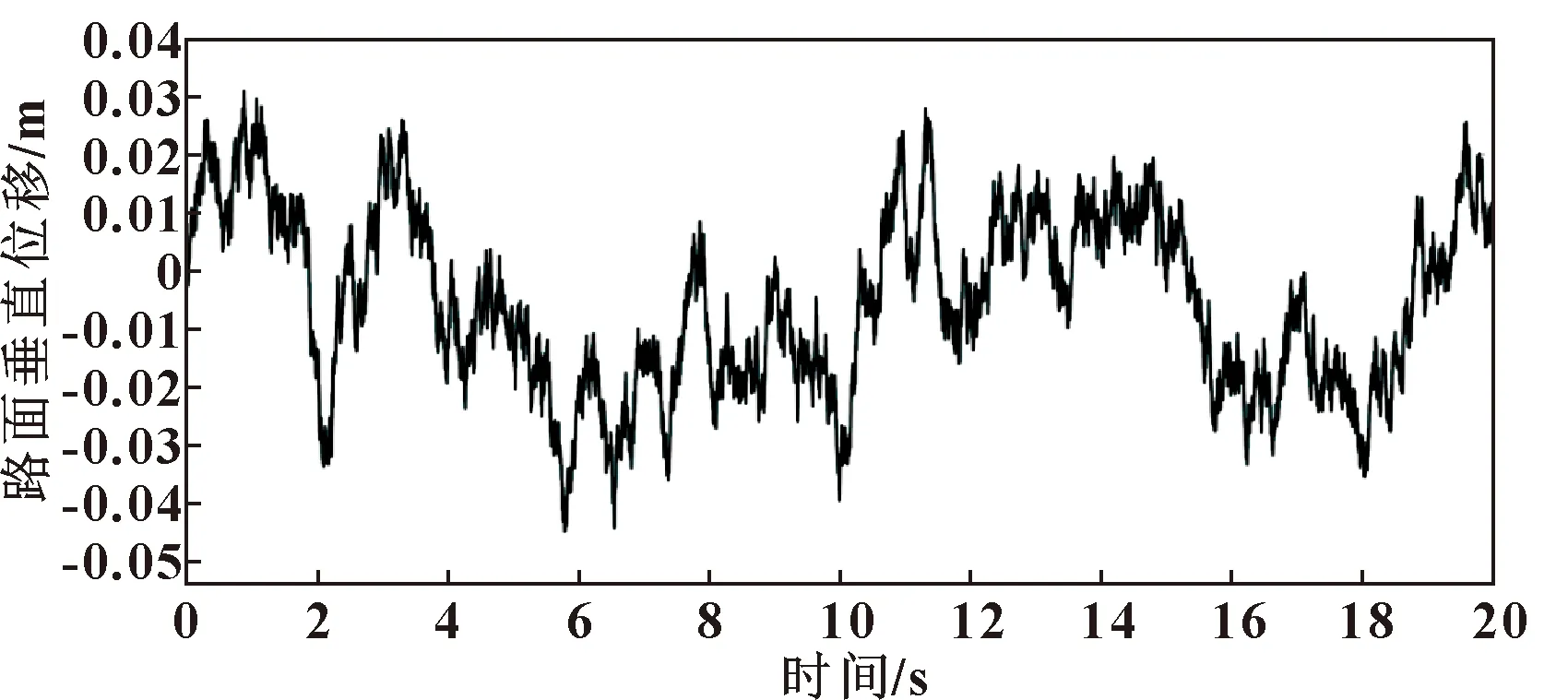
图4 B级路面车速50 km/h激励曲线
3.2 仿真验证与结果分析
利用MATLAB/Simulink仿真平台建立基于热力学的空气弹簧动力学模型,并进行联合仿真。仿真输入参数如表4所示。
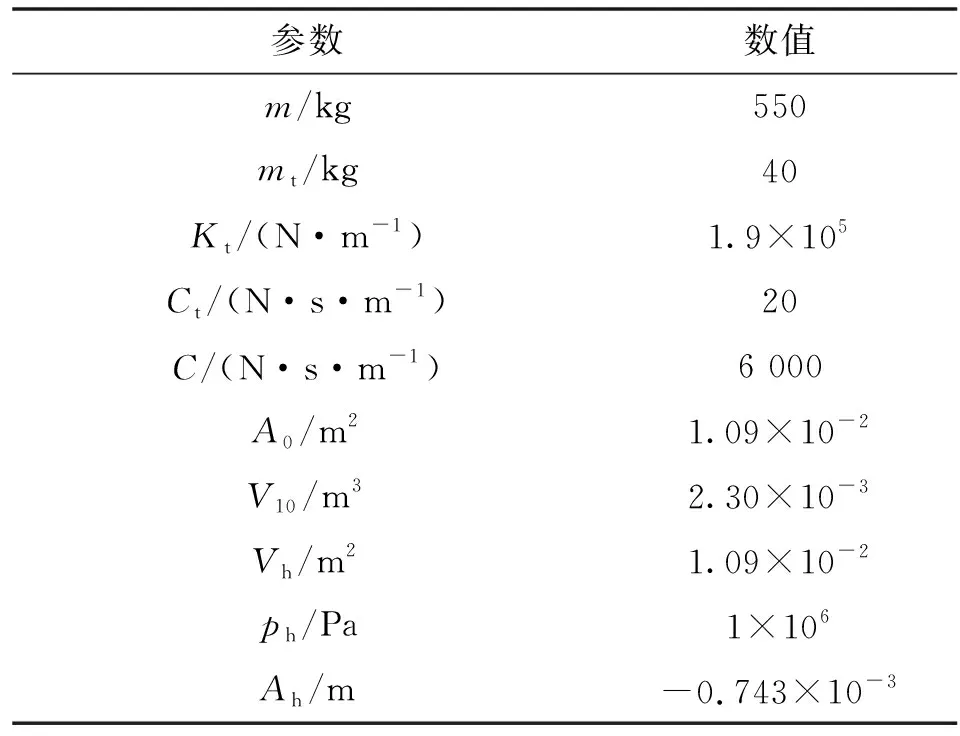
表4 仿真车辆输入参数
仿真时间设为20 s,仿真工况为系统行驶于50 km/h的B级路面时,对它进行高度调节,在初始高度0的基础上,设置上升50 mm和下降50 mm的控制操作。
图5—图8所示为车辆高度的控制情况,在高度控制情况中,对比了单纯PID控制与自适应模糊PID控制的结果,计算车身平衡位置稳定后的高度误差均方根值(Root Mean Square Error,RMSE)如表5所示,计算方法如式(8)所示。从图5—图8及表5可以看出:相较于PID控制器,采用自适应模糊PID控制器的控制效果更加明显,对于车辆上升和下降都有较好的控制能力。
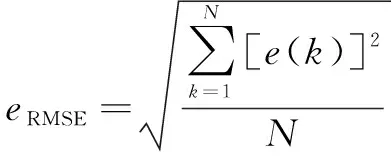
式中:为工况结束后车身平衡位置稳定时间段采样点个数;()为第个采样点对应高度与目标高度的偏差。
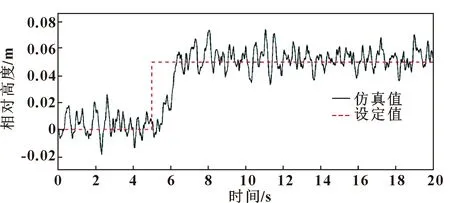
图5 车辆上升时PID动态高度控制情况
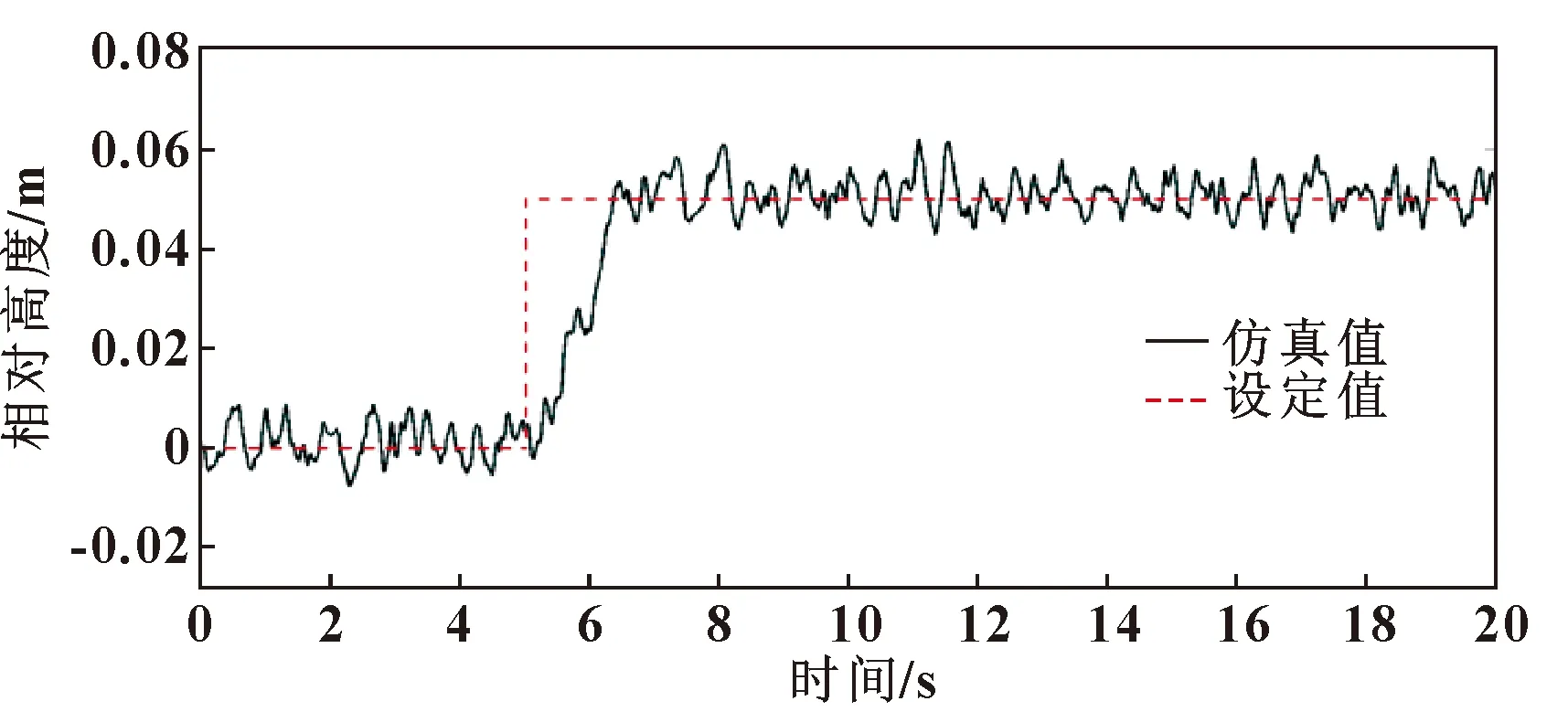
图6 车辆上升时模糊PID动态高度控制情况
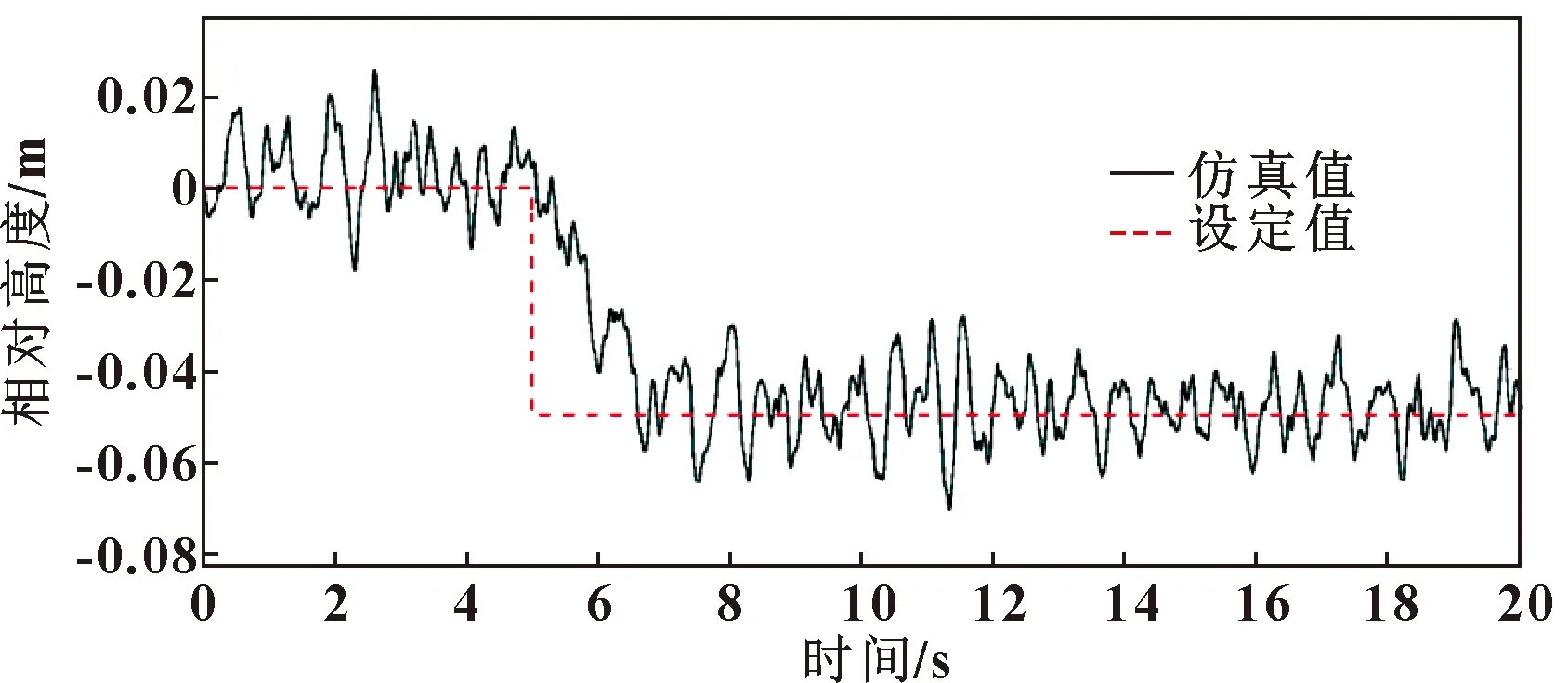
图7 车辆下降时PID动态高度控制情况
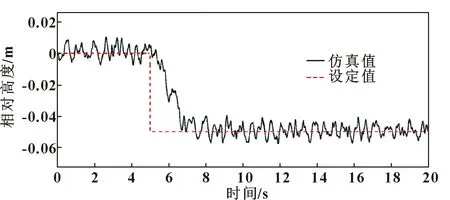
图8 车辆下降时模糊PID动态高度控制情况

表5 车身位置稳定后高度的RMSE
4 结论
通过采用热力学空簧建模的方法与自适应模糊PID控制策略,完成了空气弹簧充放气及模糊PID控制的理论分析。主要结论如下:
(1)在分析了空气弹簧充放气回路结构和工作原理的基础上,在温度-压力2个方面建立了基于热力学的空簧模型,进而建立了车身高度控制的数学模型;因热力学是自然界普遍存在的规律,所以研究结果具有普适性。
(2)基于自适应模糊PID控制方法,设计了车身高度调节控制器,并对控制器的控制效果进行了仿真分析。结果表明:采用PID控制器相比于无控制器的高度误差均方根改善率最高可以达到21.7%,提高了控制精度,提升了车辆行驶的平顺性。

