基于ESLM热机耦合结构动态优化设计
郭计云,贾权,郭巨寿,张艳岗
(1.山西大同大学机电工程学院,山西大同 037003;2.北方通用动力集团有限公司,山西大同 037036;3.中北大学能源与动力工程学院,山西太原 030051)
0 前言
等效静态载荷法(Equivalent Static Load Method,ESLM)的提出为结构动态优化提供了一种新的解决方法。然而传统的ESLM基本上研究的是单一动态机械载荷作用下的等效静态转化方法,但是实际大部分机械结构都是在多个物理场共同作用下工作的,因此多种载荷共同作用下的优化问题成为困扰众多学者的难题。为此,Jaehun LEE博士在欧洲计算流体动力学国际会议中,首次提出等效静态载荷法解决大规模结构动态优化问题时不应该仅仅局限于一个物理场,可推广到流-固耦合传热和声学结构耦合场中。对此,众多学者就机械结构的热-结构耦合分析及优化以及热等效进行了深入的研究。
高建辉等将遗传算法与“穷举搜索法”结合,采用二步递进策略对火焰筒浮动瓦块结构进行了热-结构耦合分析及优化,结果证实这种优化方法在瓦块热-结构耦合优化中的正确性。李昱霖等利用强弱耦合关系简化了气-动-热耦合问题,建立了气-动-热多学科集成分析平台,针对不同学科耗时问题,采用了增广的自适应响应面优化策略完成了气-动-热多学科设计优化,在提高颤振速度的同时,使升力面结构质量降低。唐先龙对排期歧管进行了仅考虑机械载荷、仅考虑热载荷以及热-结构耦合分析,结果证明热载荷对于排气歧管的破坏起到主导作用,在分析时不可忽略,并最终对排气歧管进行了相应的优化,优化后应力以及塑性变形都有所减小。刘云飞等利用单元节点整体坐标直接计算单元等效节点热载荷积分方程中所需要的未知量,为节点热载荷等效提供了一种新方法。胡向东、任辉在较早提出了温度场等效的思想,并以等效截面的温度场等效整体温度场。作为结构动态响应优化的有效途径之一,等效静态载荷法在处理动态约束方面的优势、解决类似碰撞问题等高度非线性动态优化问题的先进性和在求解非线性动态响应优化问题时相比于响应面法的优越性已被证明。HEDAYA等将疲劳损伤作为动态响应优化的迭代收敛判据,改进了等效静态载荷法;李永欣等提出一种基于模量比率因子的等效静态载荷计算方法,有效解决了弹塑性材料的非线性问题,在提高等效精度的同时拓展了在非线性材料方面的应用边界; XU等提出一种基于时域等效静载荷的宏观结构材料分布和周期性微观结构并行的动态拓扑优化方法;李明、汤文成利用等效静态载荷法,研究了动态响应约束下的区间参数结构可靠性拓扑优化问题,拓展了ESLM的应用范畴;张艳岗等在其研究中提出了关键时间点识别方法和基于应变能原理的动态载荷等效静态转化方法,并进一步将该方法推广至工程实际应用。
从上述文献看出,虽然对于热载荷和机械载荷共同作用下的等效静态转化研究较少,但是在理论研究和实际应用方面是得到验证的,因此,研究热载荷、机械载荷以及热-结构耦合载荷的等效转化具有一定的可行性。鉴于大部分机械结构在动态热-结构耦合作用下共同工作,研究此类问题、为动态响应优化打下坚实的理论基础迫在眉睫。
1 热机耦合载荷等效计算理论
1.1 等效静态载荷原理
等效静态载荷原理:线性静态分析中的结构等效静态载荷能够产生与对应时刻结构非线性动力学分析完全相同的系统响应场。动力学微分方程:
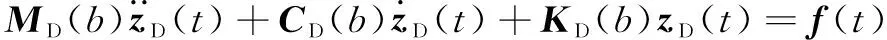
(1)
式中:为质量矩阵;为阻尼矩阵;为刚度矩阵;为结构位移、应力等响应结果;()为时刻外载荷向量。根据上述原理得到等效静态载荷表达式:
()=()
(2)
式中:为等效静态载荷作用下刚度矩阵;为动态载荷作用下每个时刻与之对应的等效静态载荷。
具体等效原理如图1所示。
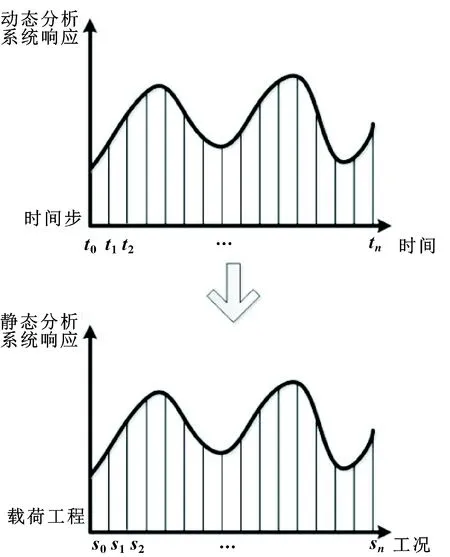
图1 等效静态载荷法原理
由图1已看出:动力学分析中计算时间步为+1步,在等效时,把每个时间步看成一个静态工况,并且要求由第个等效静态载荷的系统响应与对应时间步的动态响应相同。
1.2 热机耦合等效机制
从温度场和应变场的耦合问题入手,结合线性热应力理论推导热-力耦合问题的等效静态转化。
假设弹性体在热载荷和外界载荷作用下是一个缓慢增加的准静态过程,因此忽略了加速度项以及温度变化速度的影响。在此前提下热传导方程和平衡方程各自独立,即温度场导热方程如式(3):
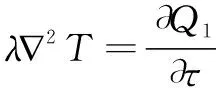
(3)
热弹性体导热方程式,取和为独立自变量,由赫姆霍尔兹自由能=-出发,两端求偏导,同时根据式(4)
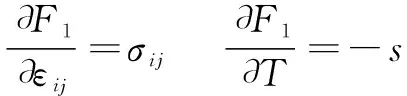
(4)
得出:
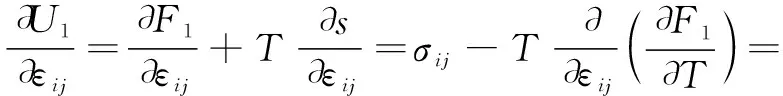
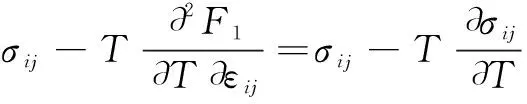
(5)
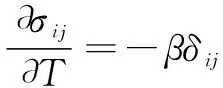
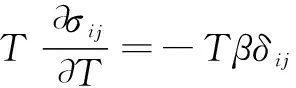
(6)
因此:
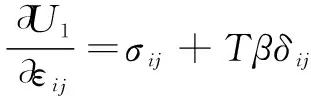
(7)
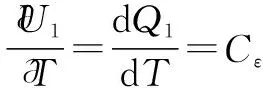
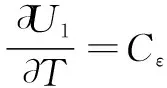
(8)
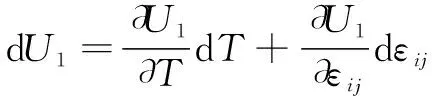
d=d+d+d
(9)
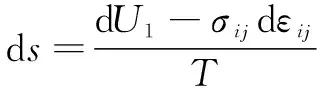
=d=d-d=d+d=
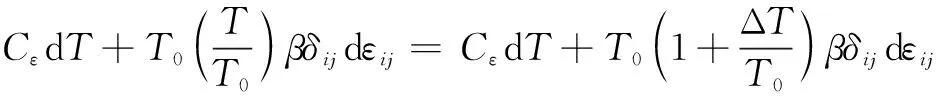
(10)
当Δ=-与相比非常小时,可近似省略Δ,则:
≈d+d
(11)
上式可写为
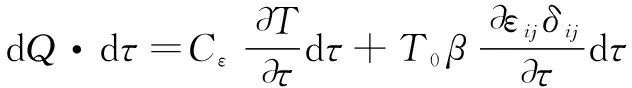
(12)
式中:d为单位时间内单元体积微元体与外界交换热量,即热流量。
另外,有三维模型平衡可知:
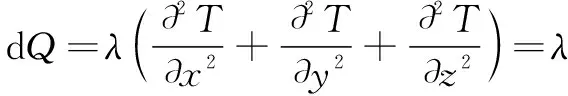
(13)
将式(13)代入(12)中得:
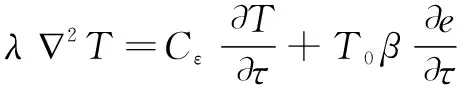
(14)
式(14)即为考虑热弹性物体微元体变形后的导热方程式(修正后的傅里叶热传导公式),与式(8)比较发现右边第二项是由变形功引起的附加项,也就意味着弹性体受到外界的热载荷作用,其中一部分引起结构温度的上升,另一部分则转化为弹性体的变形。相比传统傅里叶公式多出的部分称为温度场和应变场的耦合项,体现了相互耦合作用。
对于热机耦合等效静态转化问题,将线性热应力理论与等效静态转化理论相结合,得出:
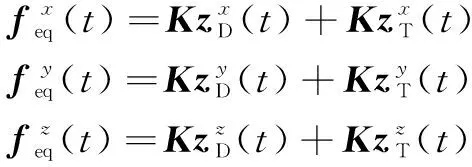
(15)

1.3 基于等效静态载荷法的结构动态优化设计流程
由基于位移的等效静态载荷公式(2)可以看出,等效静态载荷只有对结构进行瞬态分析之后才能计算得到,说明通过等效静态载荷计算的是已知的位移场。从这个角度来说,等效静态载荷没有任何意义,但是等效静态载荷最终是运用到结构优化中去。优化设计的具体步骤如图2所示。
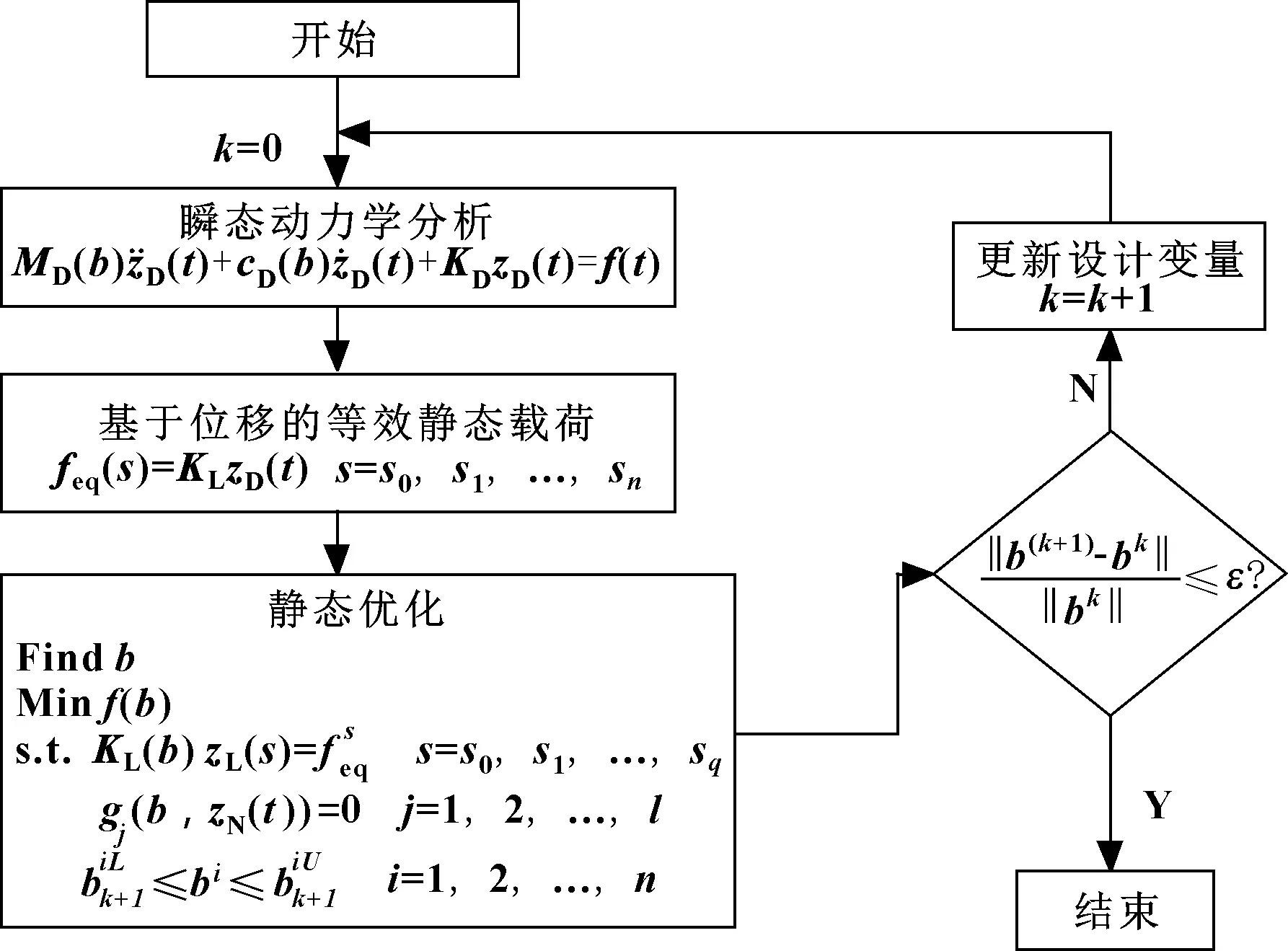
图2 等效静态载荷优化设计流程
结构在进行动力学分析后,通过选取关键时间点的关键位置点的应力、变形或应变能,通过等效静态载荷法提取静态载荷进行优化。
2 算例验证
2.1 简单实体结构验证
图3所示为一铝合金实体结构,在右端面施加动态压力,在和处分别施加100 ℃和20 ℃的温度。

图3 铝合金实体结构
选取上表面全部节点,在Isight中进行等效静态转化,选取NLPQL算法进行优化,其优化数学模型如式(16)所示,优化迭代过程如图4所示。
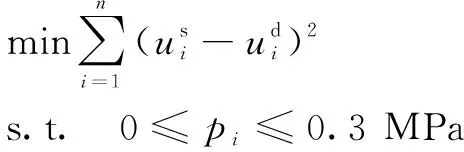
(16)
采用先分别等效热载荷和机械载荷后耦合与先进行耦合分析再进行等效的误差如图5所示。可以看出:对于动态热机耦合问题,耦合后再等效的精度高于先等效再耦合。因为对于热机耦合问题,考虑到热载荷和机械载荷相互内在关系的影响,而先等效后耦合只是同一种载荷的线性叠加,没有考虑到相互耦合作用,失去了一定的精度。然而对于一些大型的设备,不考虑不同载荷间的相互影响,先等效后耦合也是一种可以考虑的方法。但是对于文中热机耦合等效选择先耦合后等效的方法,并将其应用到工程实际结构——某柴油机活塞上,进行该方法的有效性证明。

图4 优化迭代过程 图5 两种不同等效方法的误差分析
2.2 实际应用
2.2.1 某柴油机活塞静态优化
选取典型受热机耦合载荷作用零部件-发动机活塞为对象进行对比分析。为使分析更加符合活塞实际运转工况,在Creo中建立活塞-连杆装配体模型如图6所示。
其中在Workbench中建立的活塞冷却腔的参数化模型如图7所示。
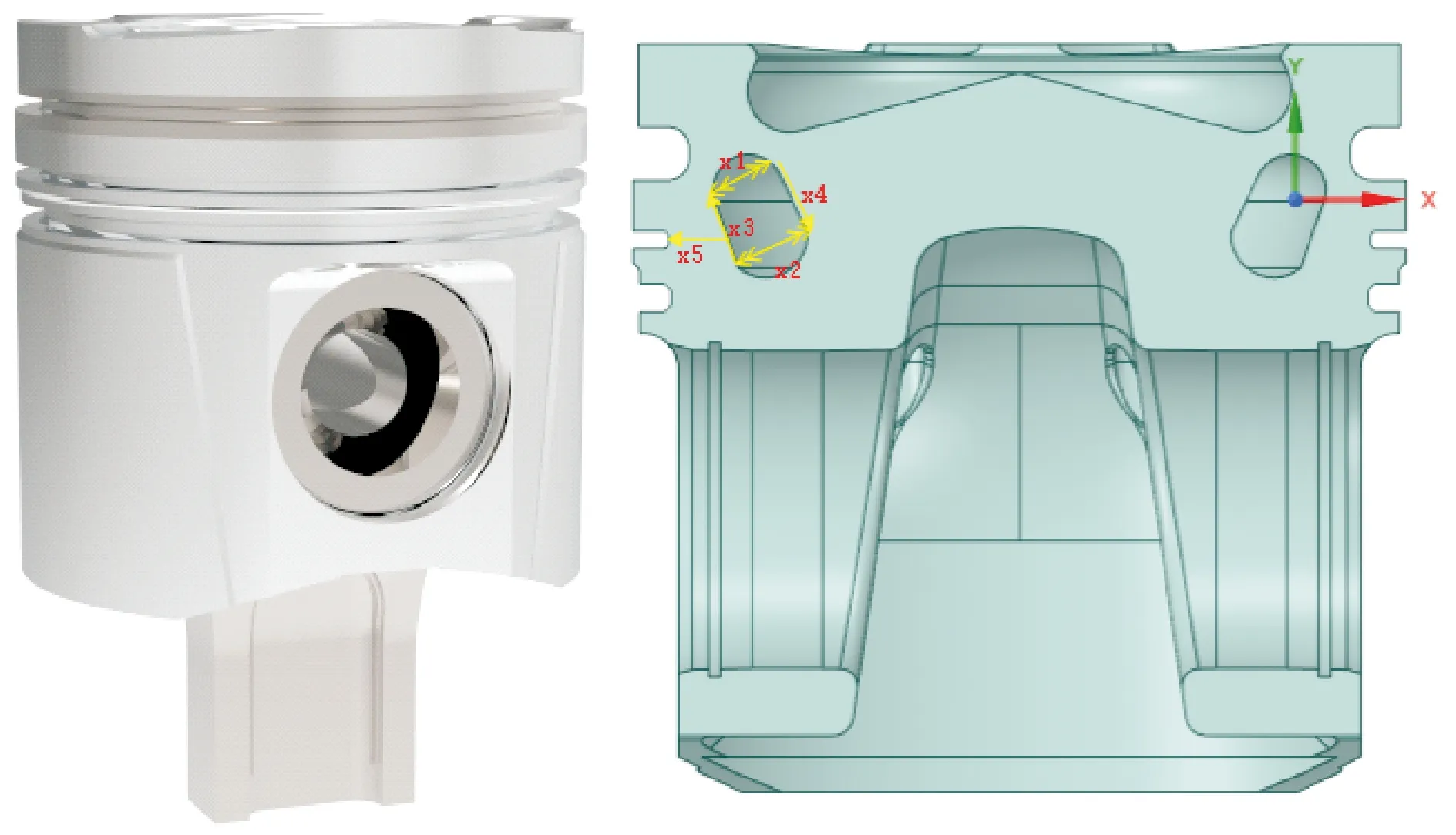
图6 活塞连杆装配 图7 活塞冷却室的参数化模型
活塞-连杆组中网格尺寸定义活塞尺寸为1.5 mm,其余部分设置为3 mm;网格划分控制为四面体网格划分,对接触面的网格进行细化,定义尺寸为0.8 mm,整体划分单元数276 154,节点数463 015。在活塞-连杆组装配体问题中,由于存在摩擦接触且摩擦因数与接触面之间的润滑情况、温度以及湿度有关,因此将活塞销孔与活塞销和连杆小头孔内表面与活塞销圆柱表面之间的摩擦因数设为0.12;设置接触算法为罚函数法,因为这种算法对于非线性问题的收敛更加容易;活塞第一环槽和镶圈设置为绑定接触,将其看成一体。活塞温度场分析采用第三类边界条件,最大压力选取为=14.5 MPa,其分布情况如图8所示。
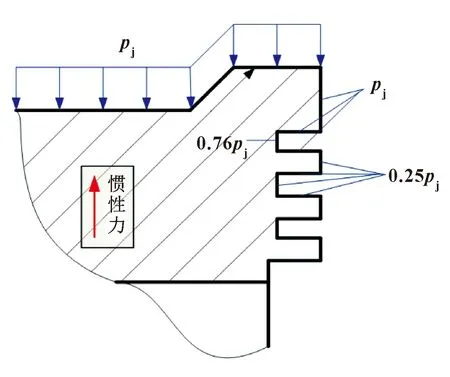
图8 活塞压力负荷边界条件
活塞静态优化以活塞的质量最小为优化目标,活塞冷却腔尺寸作为设计变量,第一环槽温度以及应力作为约束条件,构建静态优化模型如式(17)所示:
min
s.t.≤[]
≤225 ℃
≤≤
(17)
式中:为活塞质量;[]为活塞材料许用应力值;表示第一环槽温度,不超过机油结焦温度225 ℃;表示冷却腔设计变量,、分别表示设计变量上下限。
采用响应面法进行优化设计,优化算法选择多岛遗传算法。优化后的模型如图9所示。
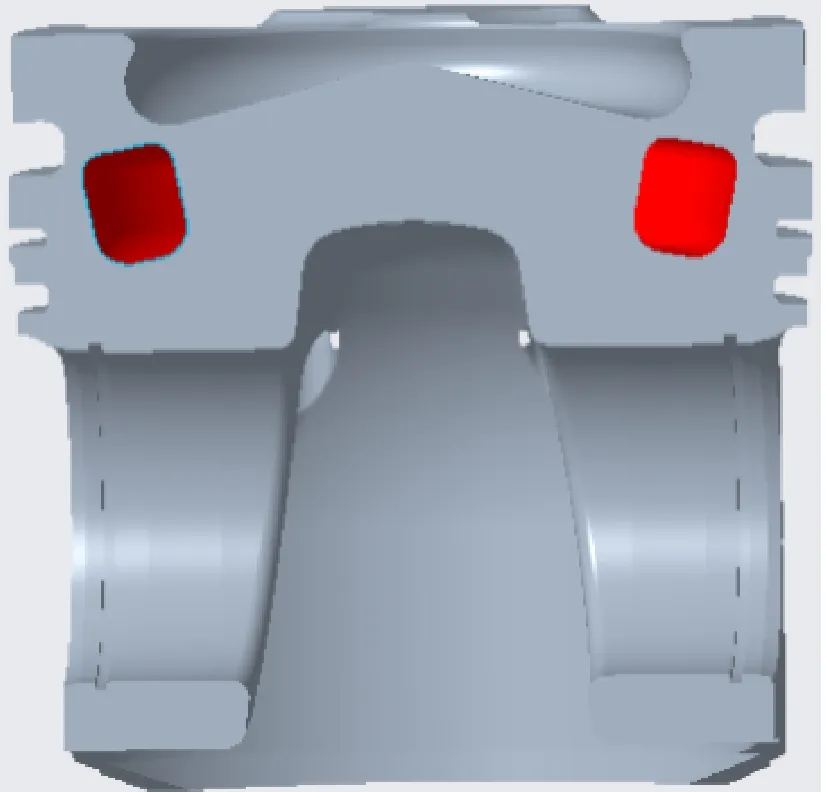
图9 活塞静态优化模型
静态优化前后质量和冷却腔参数变化如表1所示。
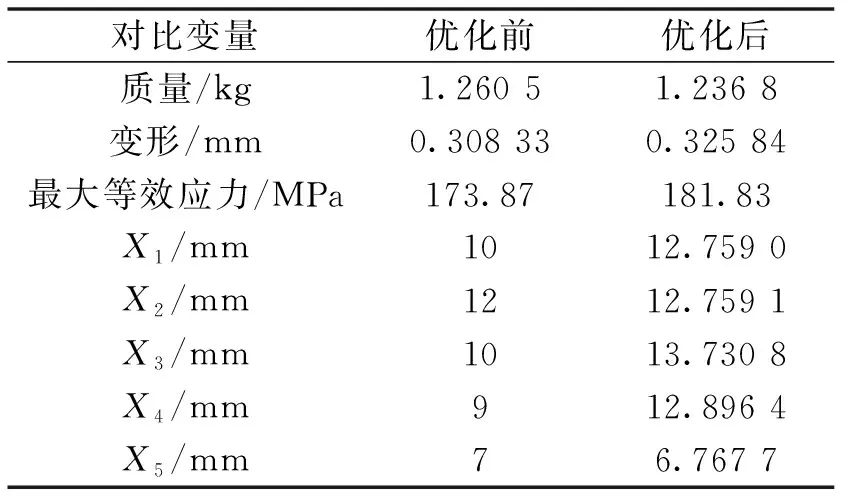
表1 活塞静态优化前后比较
活塞静态优化后变形和应力都小幅度增大,质量减少了1.88%。由此可知,对于静态优化的优化裕度比较小。
2.2.2 基于ESLM活塞动态优化
等效静态转化方法借鉴基于能量等效静态载荷法,将位移和应力同时作为等效静态转化指标,选取关键节点位移和应力如图10所示。
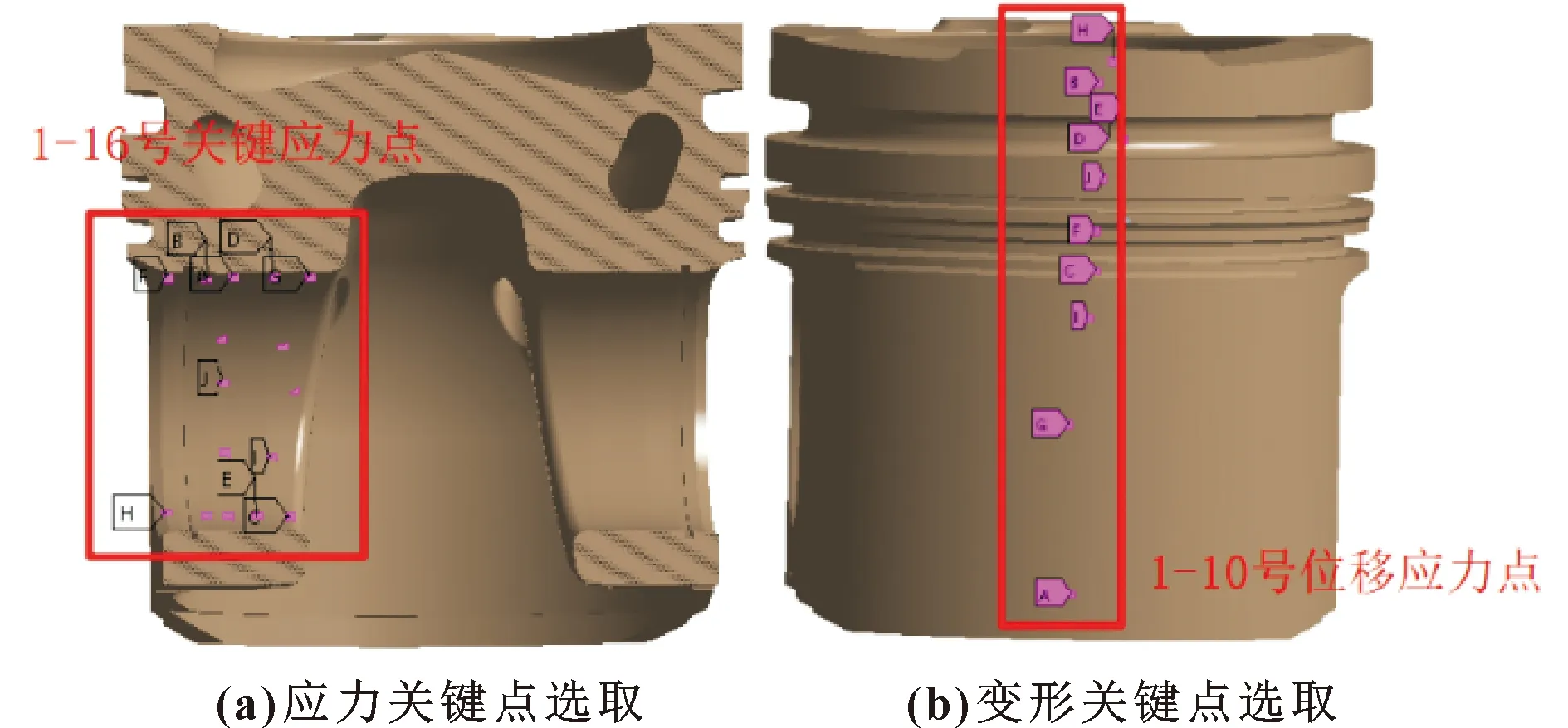
图10 关键节点和应力
等效静态转化数学模型如式(18)所示:
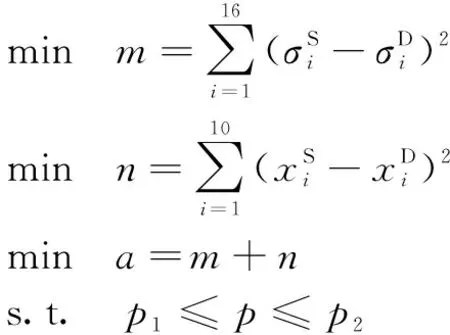
(18)
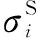
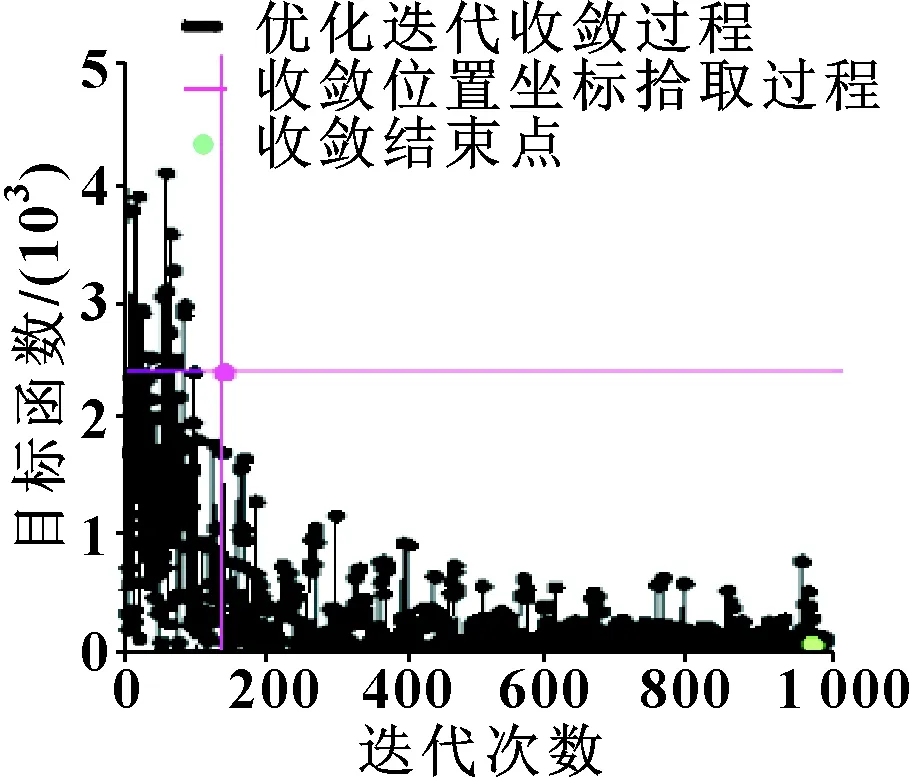
图11 迭代收敛性曲线
从图11可以看出:Isight中优化历程共迭代1 000步,收敛过程目标值不断减少,范围波动也随着优化进程越来越小,最终得到最优解。等效载荷如表2所示。

表2 优化后活塞各区域的等效静载荷值
从图12和图13可以看出:对于等效前后的关键位置点的最大等效应力值和最大位移值的最大误差均处于3%左右,在合理范围内。
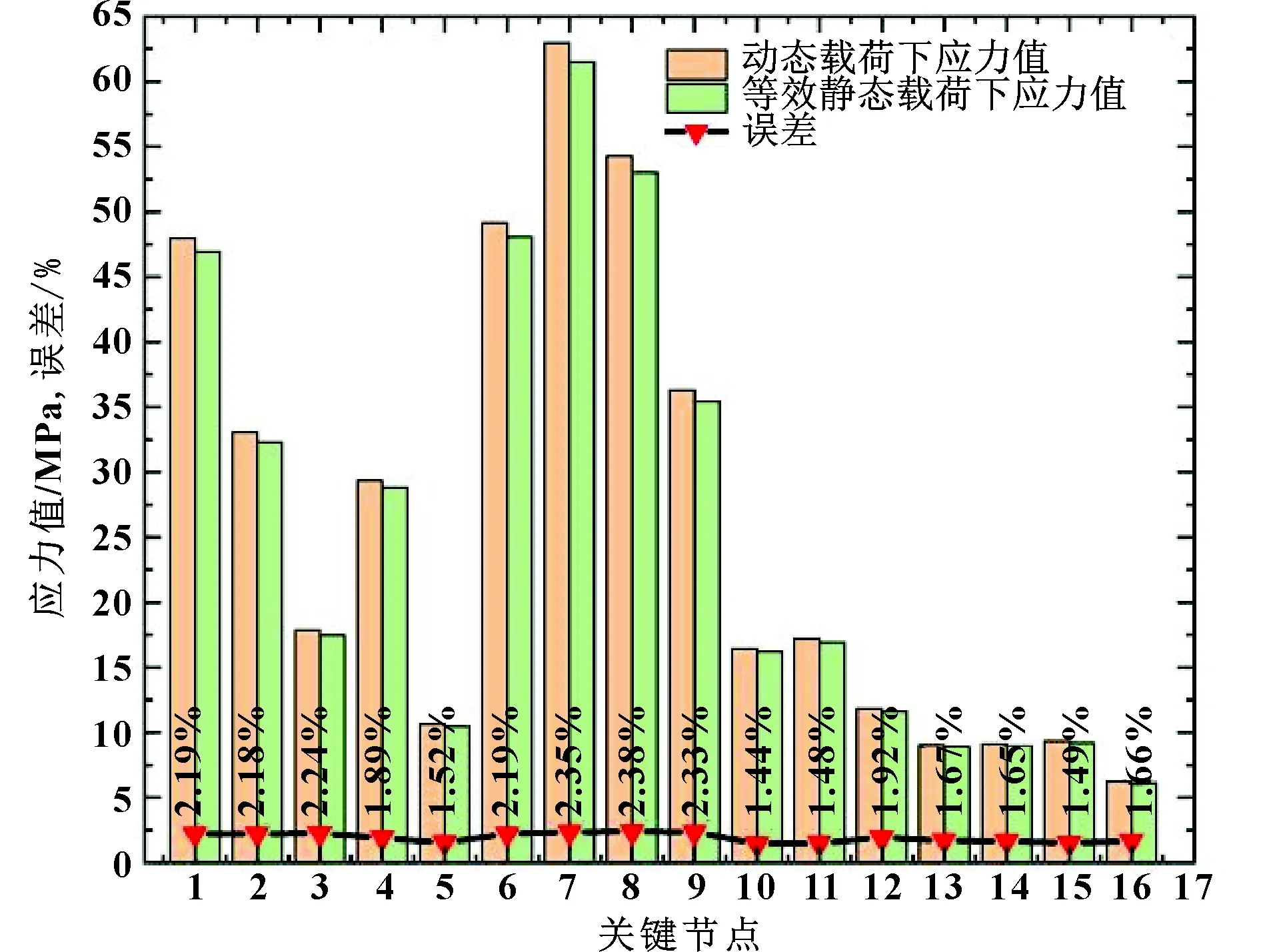
图12 关键点应力比较

图13 关键点位移比较图
对于基于ESLM活塞动态优化数学模型同静力学相同,基于等效静态载荷法优化后的数据如表3所示。
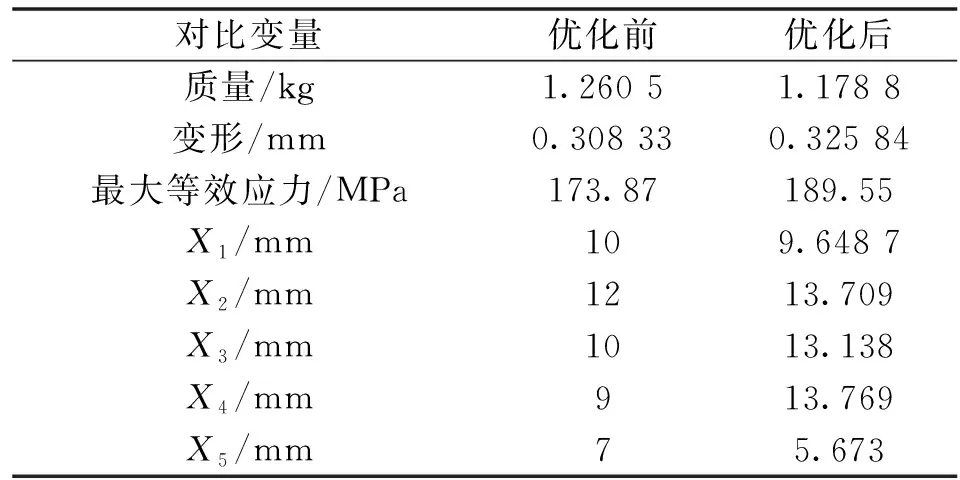
表3 基于等效静态载荷法动态优化前后比较
由表3可以看出:相比优化前,优化后质量减少了4.7%,最大等效应力及变形有所增大,但都在材料和结构允许范围内,并且较静态优化结果在活塞轻量化方面提高了4%,因此基于等效静态载荷法的动态优化设计要优于单纯极限工况下的静态优化设计。
3 结论
本文作者探索基于等效静态载荷法的动态响应优化方法在热-结构耦合场的应用,将热弹性理论与等效静态法结合,首先从理论角度推导了热载荷-机械载荷耦合作用下的动态载荷等效静态转化机制,并以实体横梁结构作为算例进行验证,通过对比等效前后节点位移值,验证了等效理论在热物理场、热-结构耦合物理场下同样适用,为基于ESLM的热机耦合结构动态优化设计奠定了理论基础。并以典型受瞬态热机耦合结构-柴油机活塞为研究对象,通过活塞热机耦合瞬态动力学分析,提取了16个关键位置点的应力、位移,进行了等效转化计算。通过与动态载荷作用结果对比分析表明:等效转化前后考察区域的最大等效应力误差在3%以内,最大位移误差在2%以内,等效转化结果可信。进一步对比分析了活塞热——机载荷作用下的静态优化和基于ESLM动态优化,结果表明:两种优化后的活塞变形、应力以及第一环槽的温度结果相近,但基于ESLM动态优化比静态优化活塞质量降低了4.7%。研究结果充分证明了基于ESLM动态优化方法的优越性。

