CDIO理念下的《C#程序设计》实验教学设计

房琛琛，齐 琪，陈 龙，薄钧戈

(西安交通大学 计算机科学与技术学院，陕西 西安 710049)

0 引 言

“新工科”改革的目标是培养工业4.0背景下的复合型人才，课程教学模式必须适应产业发展需求而提高学生解决复杂工程问题的能力，而实验教学是培养学生实践动手能力和创新能力的重要途径[1-2]。但以往的实验教学只以知识传授为重点，缺少对学生专业特点、学生兴趣及掌握情况的考虑，导致实验教学效果不理想[3]。

该文以C#程序设计课程为例，分析当前实验教学的现状，并融合学生的专业特点，设计了一个内容贯穿整个课程知识体系的实验案例。该案例以“CDIO (构思(Conceive)、设计(Design)、实现(Implement)和运作(Operate))”理念[4]为导向，以学生喜欢的游戏主题为切入点，引导学生从面向过程到面向对象的程序设计思维过渡，倡导学生通过“理论学习、方法引导、自主研学”的方式来完成综合性实验以解决复杂的工程问题。

1 当前C#程序设计实验教学现状及分析

目前C#程序设计实验教学主要存在以下几个问题[5-8]：

(1)教学内容抽象、知识点多和杂。C#是一种面向对象的语言，内容包括类、对象、继承、多态等。这些知识点比较抽象，学生难以理解，导致失去学习兴趣。

(2)传统的实验案例无法将知识点贯通。大多数实验案例都是与当周理论课知识点相对应的实验，各个实验之间的联系较少，课程结束时学生难以将课程体系的知识点融会贯通，导致遇到实际问题无所适从。

(3)教学过程和实验案例脱离实践应用。传统的教学注重理论知识的讲解，以教师讲授为中心，学生被动接受知识，对学生实际开发能力缺乏足够的重视。与之对应的实验案例也往往是“为了实验而实验”，内容呆板老套缺乏实践应用价值，难以激发学生兴趣，导致学生参与度低。

(4)学生层次不同，难以个性化培养。上课的学生所属专业不同，对计算机程序掌握的程度也参差不齐。而现阶段的教学内容和实验案例基本都是按照一致的要求来给学生传授，这种情况会导致基础好、能力强的学生得不到更深层次的学习，也会使基础弱、能力弱的学生没有很好掌握要点的现象出现。

针对上述问题，可以按照以下几点特征来选取实验案例：

(1)实验案例应来源于生产生活，最好有些趣味性，对学生而言不陌生、有代入感，能激发学生的学习兴趣；

(2)实验案例的综合性应较强，要能够涵盖“C#程序设计”的主要知识点，如类、对象、方法、继承、多态等，理论与实践要有联系；

(3)难度适中，有层次性，可拓展性好，可以引入新知识。使不同层次学生能有所学、有所思、有所得。并且能够培养学生自主学习的能力；

(4)可以根据不同的专业特点，设计案例中有不同的侧重点，使学生发挥专业特长，所学能所用。

2 “理论学习、方法引导、自主研学”实践教学模式设计

实践教学是为教学目标服务的，为了更好地解决当前实践教学存在的问题，对现有实践教学模式进行改革，该文提出“理论学习、方法引导、自主研学”的实践教学模式，具体内容如下：

(1)理论学习。实践教学以现有教材的课程大纲为基础。需掌握的知识有：

①开发环境的使用、程序调式等基本操作。

②面向对象程序设计方法的原理：类与对象、继承与多态。

③C#基本语法。

④Windows窗体程序框架、常用控件、鼠标键盘事件、绘图，事件。

⑤文件的读取、序列化与反序列化知识。

(2)方法引导。学生在老师引导下，构思(Conceive)和设计(Design)实验内容。以五子棋游戏开发为目标，分解需求。启发学生发现已掌握的知识点和分解任务的解决之间的关系(见表1)。然后对现有任务进行算法设计和数据结构定义，进入小组讨论。各组根据任务的划分情况制定系统开发框架和实施方案。

表1 知识模块和项目应用的关系

(3)自主研学。实验中期的创新基本能力培养阶段，学生自主完成(Implement)整个实验；针对本案例中的复杂问题，借助网络资源调查研究已有技术的现状和常用应用方法。通过查阅资料并编程实现，既锻炼了学生的自主学习能力，也锻炼了学生的动手实践能力。

3 融合专业特点的实验案例设计

一个好的实验案例可以让学生运用所学的知识，设计并编程实现一个复杂度较高的综合性项目。通过完成这一项目，能够让学生深刻理解如何通过计算机来解决实际问题的过程，并且提高自己的动手实践能力。

本实验案例选择五子棋，因为五子棋是一个趣味性较强，能够吸引学生去自主完成的一个项目，并且其综合性和层次性也相对较强。五子棋是一种两人对弈的纯策略型游戏，深受大众喜欢，以此为实践项目可以提高学生的学习兴趣、学生的积极性和参与度，从而达到寓教于乐的效果；由于整个项目涵盖程序设计课程绝大多数知识点，并且训练学生的设计、编码、调试、运行等多方面能力，所以在知识点覆盖和能力训练上都具有较强的综合性；整个案例中的功能从易到难，由浅入深，学生可以根据自己的能力选择其中部分功能予以实现，通过这种层次性及功能性来适应不同程度和不同专业学生的各种需求[9]。

3.1 实验案例的设计思想

本案例的主要内容是设计并实现应用软件——五子棋。五子棋是一种两人对弈的棋类游戏，基于.NET Framework平台的图形用户界面模板，既可以利用C#语言和面向对象的基本原理方便的实现，又有很强的趣味性。其中，系统的功能设计和数据结构的设计是实验的重点，研究游戏的禁手规则、人机对战算法是实验的难点。通过对五子棋软件的实现，加深学生对计算机进行问题求解过程的理解，培养学生将复杂工程问题进行“抽象、算法、自动化”的能力。

本案例涉及的内容包括以下几方面：

(1)五子棋基本规则：这部分主要包括落子规则和判负规则。根据是否对限制黑棋先行的优势，将规则分为无禁手和禁手规则。

(2)程序设计基本方法：面向对象的概念和思想、基于.Net Framework的C#图形用户界面、GDI+绘图应用、常用的类库。

(3)案例的不同侧重点：面向理科生的重点为博弈算法，因为有理科背景的学生擅长运行数学模型解决问题。面向工科生的重点是软件扩展功能的完善，如悔棋、复盘、登陆/注册、背景音乐等。

3.2 实验案例的不同侧重点

(1)面向理科生的侧重点是博弈算法。让计算机模仿人类下棋，传统的算法是采用博弈算法。该算法的数据结构就是博弈树(如图1所示)。图中A、B是对弈双方，A有多种落子的选择，那么B也就有多种对应的下法。博弈树就是把所有的走法都列出来所构成的树形图。图中的每一个节点表征博弈的一个确定状态。通常把从一个节点通向其子节点的过程称为一个行动，每一条边代表一个动作。这里还有一些名词，例如，分支因子表示节点的子节点数目；根节点表征博弈的初始状态；叶子节点表示那些没有子节点的节点；用端节点代表了博弈结束的状态，可以通过评估端节点来判断博弈的结果。

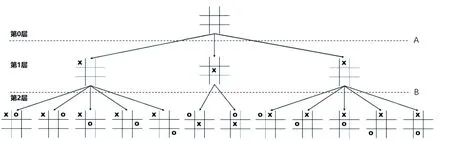
图1 博弈树

博弈算法中的子节点是以几何级数上升的，算法的任务是从这些子节点中找到一个最优的节点，从而赢得游戏。整个算法分为搜索和估值两部分，对所有可能落子位置进行一个评价就是估值，然后选择估值最高的位置作为最终落子位置。经典的算法有极大极小搜索算法和Alpha-beta剪枝算法。

①极大极小搜索算法(MinMax)。

该策略是指，在假定对手总是执行最佳动作的前提下，最大化自己的博弈收益。极小极大策略[10-11]是在各种风险最小的策略中选择收益最大的一个，从而在保证收益的同时最小化了风险，但这是以放弃最优策略为代价。因此这是一种保守的策略选择方法。在A和B的两人博弈中，A尝试最大化其收益，而B尝试最小化A的收益[12]。

对于深度为4的博弈树采用极大极小搜索算法的过程(如图2所示)，要想知道第一步怎么走，就要从第4步开始。根据树状图的可行路径，列出每一种可能的分数。第4步是对手下的，他要做的是最小化分数，于是对手根据结果可以反推出如图2中b标记边的选择。继续从后往前看到第3步，当知道了对手的选择以后，可以根据对手的结果反推出自己的选择，要做的是最大化这个分数，如图2中a标记边的选择。重复这个步骤，最终可以发现第一步的最优选择。

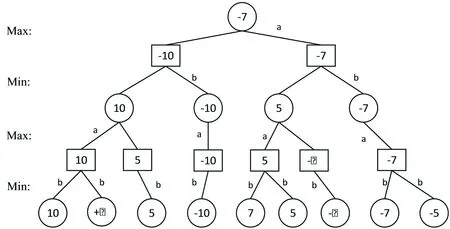
图2 极大极小算法搜索过程

②Alpha-beta剪枝。

虽然五子棋的标准棋盘是15×15，但整个搜索空间也是一个庞大的数字。为了限制博弈树的大小，通常不会对所有的状态做展开，并且只访问那些展开的状态。Alpha-beta剪枝算法[13-14]被用来减少博弈树中被极小极大策略评估的节点数目，从而缩减博弈树的规模。它的原理是在博弈树内搜索过程中判断出哪一个叶节点可以胜出棋局时，其他搜索就不需要继续了。即对选取极大极小值进行判断，剪掉获胜机率小的叶节点，从而减小搜索量，提高效率[15]。

剪枝过程如图3所示。在选择w3走的时候同时把所得alpha和beta传递下去，在经过w1->w3->w7得到f(w3)=4(同时使beta=4)后，首先进行判断：如果alpha>beta，说明这个点一定不会产生最优解了，直接返回beta=4，不用再去搜索w8和w9。因为w1在走w2这条路时得到的一个估价值f(w1)就是alpha，而w3是Min层，它会选择子节点w7、w8、w9中f的值小的作为f(w3)，所以w3在得到f(w3)=4后如果继续搜索w8、w9，只能得到比它更小的值；w1是Max层，它要修改的条件就是找到估价值比它更大的子节点，而w1目前已知的估价值f(w1)=6比f(w3)要大，所以w1不会选w3作为下一步，也就没有必要继续搜索下去。这样就剪掉了w8、w9这两个分支，直接跳出w3进入w4继续搜索。这样就实现了有效的剪枝优化。

图3 Alpha-bet剪枝算法过程

(2)面向工科生的侧重点是软件的扩展功能的完善。扩展功能可以包括以下内容：

①悔棋：可以允许玩家一方悔一步或多步棋。

②复盘：下棋结束后重现下棋的过程，玩家可以根据此过程分析和研究成败得失和着法优劣。

③时限：可以通过设置玩家下棋的时间限制来增加游戏难度。

④登陆/注册：用户可以通过注册来设置用户名、密码等信息，然后通过登陆进入游戏环节。

⑤音乐：可以设置背景音乐或音效使玩家有良好的游戏体验。

⑥页面美化：可以添加背景图片、设计页面布局等完成美化功能。

软件的扩展功能不局限于此，学生可以根据自己的能力添加更多的功能。

3.3 实验案例的实现

(1)棋盘和棋子的实现。

棋类游戏最核心的数据结构是棋盘，棋盘表示的高效与否决定了棋类游戏的性能。棋盘数据结构的设计应该根据系统的设计目标而定。可考察棋盘的两种数据结构表示。

①二维数组。

五子棋棋盘上的任意一个位置都可以用横纵坐标来确定，因为棋盘是规则的长方形。这样就可以用二维数组直观清晰地表示棋盘结构。因为行和列的二维信息比较清楚，所以用二维数组存取数据是比较高效的。但是，也有缺点，要确定棋子状态，需要扫描整个棋盘，也就是遍历存储棋盘的二维数组才能获得特定棋子的状态，这点是比较耗时。

②链表。

如果用数组来保存棋子的信息，很难体现出棋子之间的位置(前、后、左、右)关系，这是因为单个数组元素保存的信息太少。在系统进行一些复杂的操作也是十分低效，例如悔棋，该功能是退回到上一步，因此需要知道上一步的下子位置。解决这些问题可以用链表结构。因为链表可以存储上个节点和下个节点的位置信息，因此可以用链表把用户下子的顺序链接起来。用链表不光可以存储棋子位置的横纵坐标值，还可以存储其他信息，例如，棋子的归属信息，即是我方还是敌方的棋子。

(2)绘制棋盘和棋子。

绘制棋盘的过程在private void Form1_Paint(object sender, PaintEventArgs e)事件中利用GDI+绘图函数DrawLine()画出一个棋盘。定义棋子类，包含棋子的坐标、状态、评分等信息。

(3)落棋判断。

首先收集棋盘已有棋子的状态信息。在禁手模式下，黑棋(玩家)落子时会检查是否形成三三、四四、长连。如果是，该位置提示不可落棋。黑棋(AI)落子时，首先将所有可形成三三、四四、长连的禁手位置集合标记。通过博弈算法实现搜索时，对于不属于禁手位置集合的点，采用估值函数给每个点打分，得到最优位置。在无禁手模式下，只要落棋位置空，即可落子。

第一种搜索算法：极大极小搜索算法。其伪代码如下所示：

极大极小算法伪代码(参考)

01：int MaxMin(position,int d)

02：{

03： int bestvalue,value;

04： if(game over) //检查游戏是否结束

05： return evaluation(p);// 游戏结束

06： if(depth<=0) //检查是否是叶子节点

07： return evaluation(p);//返回估值

08： if(max) //极大值点

09： bestvalue=-INFINTY;

10： else //极小值点

11： bestvalue=INFINTY;

12： for(each possibly move m)

13： {

14： MakeMove(m); //走棋

15： value=MaxMin(p,d-1);

16： UnMakeMove(m); //恢复当前局面

17： if(max)

18： bestvalue=max(value,bestvalue);//取最大值

19： else

20： bestvalue=min(value,bestvalue);//取最小值

21： }

22： return bestvalue;

23：}

另一种搜索算法：Alpha-beta剪枝算法。其为代码如下所示：

Alpha-beta剪枝算法伪代码(参考)

01： int AlphaBeta(nPlay,nAlpha,nBeta)

02： {

03： if(game over)

04： return Eveluation; //胜负返回估值

05： if(nPly==0)

06： return Eveluation; //叶节点返回估值

07： if(Is Min Node) //判断节点类型

08： { // 极小值节点

09： for(each possible move m)

10： {

11： make move m; //生成新节点

12： score=AlphaBeta(nPly-1,nAlpha,nBeta)

13： unmake move m;//撤销搜索过的节点

14： if(score

15： {

16： nBeta=score;//取极小值

17： if(nAlpha>=nBeta)

18： return nAlpha;//alpha剪枝

19： }

20： }

21： return nBeta;//返回最小值

22： }

23： else

24： {//取极大值的节点

25： for(each possible move m)

26： {

27： make move m; //生成新节点

28： //递归搜索子节点

29： score=AlphaBeta(nPly-1,nAlpha,nBeta)

30： //撤销搜索过的节点

31： unmake move m;

32： if(score>nAlpha)

33： {

34： nAlpha=score;//取极小值

35： if(nAlpha>=nBeta)

36： //Beta剪枝

37： return nBeta;

38： }

39： }

40： return nAlpha;//返回最小值

41： }

42：}

(4)游戏胜负的判定。

当有一方获胜时，最后一颗棋子的落棋处必然存在5子相连的棋型。其中连线的方式有：横、竖、左对角线、右对角线四种(如图4所示)。在实现阶段，需要在各棋子落下时，以该棋子为中心位置判断它的四种方向上是否存在五子相连。

图4 五子相连的四种情况

(5)背景音乐的添加。

通过using System.Media语句引入用于播放声音文件类的命名空间，然后通过声明SoundPlayer类的对象来实现音乐播放的功能。

音乐播放伪代码(参考)

01： SoundPlayer bgm = new SoundPlayer(音乐文件路径);

02： bgm.Play();//开始播放音乐

03： bgm.Stop();//停止音乐播放

软件扩展功能较多，其他功能不在此一一列举。

3.4 实验案例的考核与验收

本案例建立面向全过程的多元化课程考核形式，将体现自主探究过程的课堂和课后表现、项目实践等纳入实验综合考评体系，合理设置权重系数。成绩采用百分制，占比如下：

(1)平时成绩(10%)；是否按时参加实验课，是否积极参加小组讨论。

(2)基础功能完成(40%)：基本功能是否运行正确，代码书写是否规范。基础功能内容如表2所示。

(3)提高功能完成(30%)：提高功能是否运行正确，代码书写是否规范。提高功能内容如表2所示。

表2 功能实现的两个层次

(4)项目答辩(10%)：答辩时表述问题需要有一定的条理性和逻辑性，回答问题需要正确和准确。

(5)实验报告(10%)：以论文形式书写报告，掌握科学论文的书写格式、书写方法及参考文献引用等，需要体现其规范性和完整性，实验报告需要有以下内容：

①问题描述。描述本案例实验背景、需要解决的问题，涉及的知识点，问题规模，难度、调研情况。

②系统设计。重点阐述实验的设计总体思路，包括功能设计和界面设计。

③实现方法。运用了哪些核心技术，引用所查阅的资料，如教材、论文、网站等。

④实现过程。详细描述实验过程，重点记录关键步骤并解释说明，粘贴相关代码。

⑤实验结果。设计测试用例，程序运行结果截图。

⑥实验总结。总结在实验中学习和掌握了哪些知识，个人哪些方面能力有提高，案例还有哪些改进的地方。

3.5 实验案例的应用

本案例已纳入本校《C#程序设计》课程的实验教学中，面向全校的数学、化学、生物、信息专业的大二学生开设。平均每年有近10个教学班400余名学生完成本案例的实践。经过近两年的教学案例的实施，学生程序设计能力得到明显的提升。学生作品如图5所示。

图5 学生作品

4 结束语

本案例通过实现一个趣味性很强的游戏，引导学生思考如何将所学知识和现实应用联系起来。案例内容涉及到C#程序设计课程中的核心知识点，通过构思、设计、实现和运作过程，循序渐进地将相关知识点融入案例的任务中，帮助同学建立知识的前后联系。使同学体会到知识的系统性和应用性。

根据学生不同的专业特点，设计了案例中有不同的侧重点，并从不同层次的功能实现入手，提高学生的动手实践和自主研学能力，最后使之形成终身学习的习惯。

该案例目前在实验教学中进行了实际应用，学生反馈编程能力增强了，学习效果良好。