基于数学模型的机器人轨迹自动控制系统设计
吕爱玲
(青岛市技师学院 山东 青岛 266229)
0 引言
1 硬件设计
1.1 无线传感装置
为了实现对机器人轨迹的有效控制,对其周围环境数据进行准确采集是十分必要的[3]。为此,本文将新型的非接触式无线位移传感器IRWY101-2.0作为系统的数据采集装置。IRWY101-2.0中搭载了以BeeLPW协议为基础的BeeHMI组态软件,可以自组织形成星型网络拓扑结构,消除了长电缆传输带来的噪声干扰,为无线数字信号的稳定传输提供保障[4]。采集的数据实时无线传输至计算机传输速率最大可以达到200 Kbps,通信距离可达2 000.00 m。不仅如此,IRWY101-2.0的整个测量环境具有较高的测量精度和抗干扰能力,借助无线传感器节点可以组成庞大传感器网络,可以同时支持上百个测点同时进行数据采集,以此确保机器人运行距离采集的可靠性[5]。在结构设置上,其具有紧凑,体积小巧,便于安装的特点,重量仅为110.0g,尺寸大小也仅为(长×宽×高)122.0 mm×60.0 mm×50.0 mm,这也降低了机器人的运行荷载负担。在数据采样阶段,其频率最高为1.0s/次,最低为3.0 min/次,因此可以适应不同运行环境下的数据采集需求。
1.2 开发板装置
对机器人估计的控制主要是根据实时运行数据对其进行快速调整,因此要求开发板装置具有良好的运行效率[6]。本文将ULX-V26核心板作为系统的开发载体,其内置了ARM Cortex-A7内核,运行主频可以达到900 MHz,完全可以满足机器人的运行控制需求[7]。表1为以1 mm间距设置的140 PIN邮票孔提供的外设资源。

表1 ULX-V26核心板外设资源
从表1中可以看出,ULX-V26核心板具有丰富外设资源,高速10层PCB为电路的稳定运行提高保障,在140 PIN引脚的支持下,节省了连接器相关成本投入。
2 软件设计
2.1 构建机器人运动数学模型
在笛卡尔坐标系中,本文以机器人的运行线速度和角速度对运行状态进行表示,其计算方式为
其中,x、y分别表示机器人在笛卡尔坐标系中两个方向上的位置,λ表示机器人的运行航角,v和ω分别表示线速度和角速度。
以此为基础,本文以机器人自身的结构设计为基础,构建了运动数学模型,其可以表示为
其中,r表示机器人的车轮半径,d表示机器人左右车轮之间的距离,αl和αr分别表示左右车轮转动的角速度。
考虑到在运行过程中,存在约束力,因此在αl和αr运行状态下,机器人的运动数学模型可以表示为
根据研究数据,在二甲双胍与吡格列酮联合治疗下观察组病患Hb AlC、TG、TC、HDL-C分别降至(5.94±0.26)%、(3.94±0.51)mmol/L、(1.41±0.17)mmol/L、(1.03±0.14)mmol/L,同期明显优于对照组。在临床疗效上观察组也更具优势,证实在两种对血糖控制均具效果的药物联合作用下病患餐后2h血糖与FPG均可得到更显著控制,可逐渐改善病患糖化血红蛋白,让2型糖尿病得到更有效的控制。总之,吡格列酮联合二甲双胍对2型糖尿病的临床治疗相对于药物单用而言效果更显著,具有临床应用价值。
其中,e表示科里奥力系数,k表示离心力系数,p表示拉格朗日系数。
通过这样的方式,本文设计系统只需要拟合目标运行轨迹与机器人运动数学模型之间的关系,即可实现对其的精准控制。
2.2 机器人轨迹自动控制
当目标轨迹的为直线,IRWY101-2.0采集到当前位置与目标位置之间的距离后,ULX-V26对机器人运行状态的控制结果可以表示为
其中,tz表示机器人直线运行时间,L表示IRWY101-2.0采集到的距离信息。
当目标轨迹的为弧线,IRWY101-2.0采集到当前位置与目标位置之间,并根据圆心的位置,利用ULX-V26对机器人运行状态进行控制,其可以表示为
其中,th表示机器人弧线运行时间,β表示以圆心位置为顶角,以机器人位置与目标位置边形成的夹角度数。
通过这样的方式,实现对机器人轨迹的自动化精准控制。
3 系统测试
在上述基础上,本文利用MatLab软件对设计系统的控制效果进行仿真分析。
3.1 测试参数设置
在测试阶段,设置机器人的移动速度分别为3.0 cm/s和5.0 cm/s,为机器人建立了相应的作业任务,具体的目标路线见图1。
按照图1所示的方式设置机器人的作业任务,其中,a点为起始位置,对应的坐标参数信息为(0,0),b点为第1个转折点,其角度大小为120°,与a点之间的距离为20.00 cm,对应地,b点的坐标参数信息为(20.00,0),c点为第2个转折点,转折后运行轨迹与原始轨迹之间的夹角为60°,与a点之间的距离为30.00 cm,对应c点的坐标参数信息为(35.00,25.98),在运行35.00 cm后,得到d点,以a点和d点之间的指向距离为直径,以二者之间的中点为圆心,进行运行,经过a点后,最终停留在d点,其中,d点的坐标参数信息为(0,25.98)。
以此为基础,利用本文提出的控制方法进行实验测试,并将夏贤铃等[3]提出的基于网络传感器融合的移动机器人运动轨迹控制方法,姚俊等[4]提出的基于自适应滑模控制器的Stewart平台运动轨迹控制方法作为测试的对照组,分析3种方法的控制效果。
3.2 测试结果
在对测试结果进行分析阶段,考虑到轨迹控制主要是以准确度和精度为控制目标,因此本文分别统计了直线运行和弧线运动部分,不同控制方法下机器人的运行轨迹与目标轨迹之间的差异。其中,不同速度下的直行运行轨迹控制结果具体见表2和表3(表中“-”表示实际运行距离小于目标轨迹,“+”表示实际运行距离大于目标轨迹)。

表2 移动速度为3.0 cm/s时直线运行轨迹控制对比表
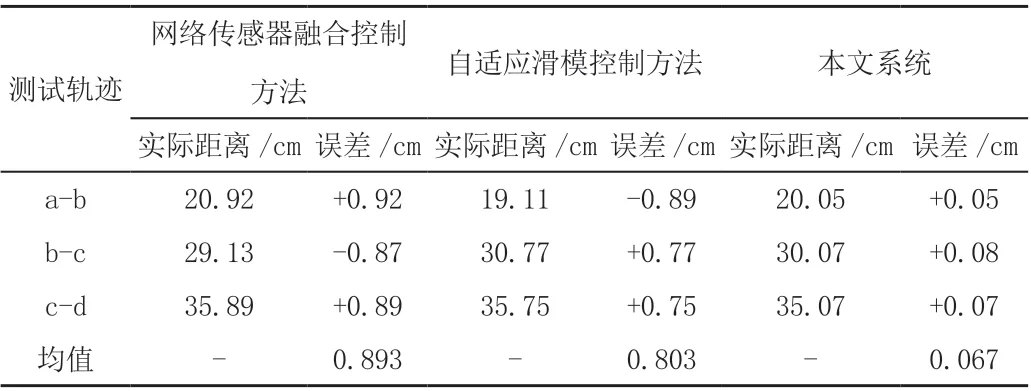
表3 移动速度为5.0 cm/s时直线运行轨迹控制对比表
从表2中可以看出,当移动速度为3.0 cm/s时,在3种测试方法中,网络传感器融合控制方法对机器人移动距离的控制误差最大值达到了0.62 cm,最小值也达到了-0.49 cm,且通过运行误差的分布情况可以看出,其表现出了较高的不稳定性;自适应滑模控制方法表现出了与网络传感器融合控制方法相似的控制结果,机器人的移动距离的控制误差最大值达到了0.50 cm,最小值也达到了-0.47 cm,虽然与网络传感器融合控制方法相比有一定的提升,但是整体误差仍处于较高水平。相比之下,在本文设计系统的控制作用下,机器人移动距离误差始终低于0.10 cm,其中,最大值仅为0.07 cm,最小值仅为0.04 cm。表明本文设计的控制系统能够确保机器人按照目标轨迹实现高精度运行。
从表3中可以看出,当移动速度为5.0 cm/s时,在3种测试方法中,对机器人移动距离的控制误差与移动速度为3.0 cm/s时相比均出现了一定程度的增大。其中,网络传感器融合控制方法误差最大值达到了0.92 cm,最小值也达到了-0.87 cm;自适应滑模控制方法误差最大值为-0.89cm,最小值也达到了0.75cm,两种方法均表现出了较大的误差增幅,表明随着移动速度的增加,其控制精度明显降低。相比之下,本文设计系统的控制作用下,机器人移动距离误差仍然始终低0.10 cm,其中,最大值仅为0.08 cm,最小值为0.05 cm,对其误差均值进行分析,与移动速度为3.0 cm/s时的差异仅为0.014 cm。表明本文设计系统能够在不同运行速度下实现对机器人直线运行轨迹的高精度控制。
在此基础上,对比了不同速度下的弧线运动轨迹控制效果,见图2。
从图2中可以看出,对比3种方法,当机器人的移动速度为3.0 cm/s时,弧线运行轨迹与目标轨迹之间的拟合度均表现出了较高水平,相比之下,网络传感器融合控制方法的轨迹偏离程度更高,自适应滑模控制方法次之,本文系统控制下,其轨迹与目标轨迹的最为相近。但当机器人的移动速度为5.0 cm/s时,3种方法的控制效果表现出了明显的差异性,其中,自适应滑模控制方法下,机器人轨迹的偏离程度明显提高,网络传感器融合控制方法下的偏离程度也发生了一定的增加。而本文设计系统下,其轨迹与目标轨迹之间的偏离程度未出现明显的变化。测试结果表明,本文设计系统能够在不同运行速度下实现对机器人弧线运行轨迹的高精度控制。
4 结语
本文提出基于数学模型的机器人轨迹自动控制系统设计研究,适应了不同运行速度下的控制需求,实现了对直线和弧线运行轨迹的高精度控制。通过本文的研究,以期为机器人在更多领域内的应用提供帮助。

