风电场的经济成本预测与管理策略优化研究
陈蕾,闫志龙,李敏,曹九发,张可
(1. 南京邮电大学通达学院商学院,江苏 扬州 225127;2. 扬州大学电气与能源动力工程学院,江苏 扬州 225127;3. 英大泰和人寿保险股份有限公司,北京 100010)
在环境和能源问题的日益严重情况下,风能技术的发展越来越受到人们重视。在风电场的前期建设中,风电场的区域和面积是已经确定好的。那么在已确定好的面积上,风电场的发电能力和经济效益都主要由布局来决定。为了能在已知的风电场上获得较多的经济利益,风电场项目开发商不仅需要考虑风电场的经济成本,还需要考虑风电场的发电能力。因此,首先需要一个准确的风电场经济成本预测方法来确认建造风电场的投入成本。
对于风电场经济成本预测方法,国外的研究相对较早。文献[1]提出了风电场的全生命周期成本。 OLIVEIRA[2]对计算风力发电项目成本的各项参数进行详细的说明,同时给出了度电成本LCOE(Levelized Cost Of Energy)的计算方法。MORA等[3]提出了一种新的理论成本模型框架,该框架包括了迄今为止海上风电场规划中通常忽略的融资要求,在风速预测相关的开发支出和融资成本之间找个平衡点,即度电成本最小化。CASTRO 等[4]对漂浮式风电场的度电成本进行了灵敏度分析,提出了一种计算特定海上漂浮式风力机的 LCOE 值。MYHR等[5]对海上漂浮式风力发电机概念的能源成本进行了全面的分析和比较,表明 LCOE 的大小取决于海岸的深度和离岸距离。IOANNOU等[6]为了增加能源成本模型的确定性成本,采用蒙特卡洛模拟得到 LCOE 的联合概率分布。SRENSEN等[7]提出了海上风电场的成本模型,并更侧重与风电场的运行与维护成本。
风电场布局管理优化可以有效提高风电场的经济效益。传统风电场布局优化主要是根据尾流效应、风机安装等因素对风机位置进行优化。但近年来,考虑的因素更多,如噪声、风电场度电成本等,为风电场中的风机布局提供更可能的方案。参考文献[8]以能源和噪声为目标函数,考虑了土地所有者、生态环境和现有基础设施相互作用对土地利用的限制;对风电场的布局进行了多目标优化。参考文献[9]考虑了布局的尾流效应,并对其进行了优化设计。
本文主要采用基于工程运用的尾流模型即2D Jensen尾流模型,计算出风电场的年发电量。同时建立海上风电场的成本模型,得到风电场的经济成本。最后利用遗传算法对风电场的经济成本和发电功率进行优化,从而得出较优的风电场的经济成本管理和风电场布局的方式。
1 风电场的经济成本模型
1.1 投资成本
风力机组的投资成本主要包括风力机组成本、支撑架成本、电网成本和电力基础设施成本(如规划成本、变电站成本和出口电缆成本等)等。
1)风力机组价格
根据文献[7],本文将风力机价格进一步提高2%,以大致涵盖迄今为止(即2019年)风力机价格的变化。风力机的最终价格表示如式(1):(百万欧元,MEUR)
CWT=1.25(-0.15+0.92PG)
(1)
式(1)中:PG为安装风力机的额定功率,MW。
2)支撑结构成本
风力机支撑结构的成本和类型取决于风力机的尺寸和水深。单桩基础被认为是浅水区的优势,在这种情况下,这意味着水深下降最多到35 m。单桩支撑结构的成本(MEUR)可通过一阶近似简化为:
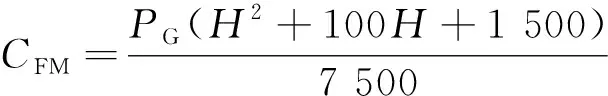
(2)
导管架支撑结构的成本(MEUR)可通过一阶近似简化为:
(3)
式(2)~(3)中:H为风力机水深,m。
3)电网成本
假设内部电网网络主要沿二次电网的一个方向布置,除了备用方向的一条连接线,给出了LC电网电缆的总长度。
LC=SD(NT-1)
(4)
式中:S为风力机组间标准间距;D为风力机组风轮直径,m;NT为风电场风力机数。海上风电场每米电网的财务成本,包括电缆成本和安装成本,取CC=675 EUR[7]。因此,得出总的风电场电网成本如式(5):
CG=LCCC
(5)
4)其它额外投资成本
本文根据ENS报告[10]提供以下相对额外成本:(1)规划、开发和融资10%;(2)变电站9%;(3)出口电缆线3%;因此,总占投资成本22%。在上述成本中,出口电缆的成本是可变的,其取决于风电场到海岸的距离。假设上述出口电缆的成本与距海岸约20 km的平均距离γref有关,可通过将成本分为固定成本和可变成本来获得以下的成本估算。
(6)
式(6)中:CP是规划成本,Cs是变电站成本,Cγref是20 km出口电缆的成本,γ是风电场离岸距离,γref是参考距离(定义为20 km),Cadd(γ)为额外成本所占总成本比例。
5)总的投资成本
所有投资成本可将上述提及的各部分成本按以下公式进行组合:
Ctotal=Cadd+NT[CWT+γFCFM+(1-γF)CFJ]+CG
(7)
式(7)中:γF表示支撑结构中使用单桩支撑结构的比例,NT表示风力机数量。所以,风电场总投资成本可以表示为:
Ctotal=(NT[CWT+γFCFM+(1-γF)CFJ]+CG)/
(8)
1.2 运维成本
据文献[7]可知运维成本(不包括运输成本)一般需要考虑风力机的尺寸和风力机间间距。可以合理的假设,在相同负载情况下,风力机的尺寸效应与特定的负载水平无关。因此,将假定大小和负载依赖性可以分解为:
CO&M,base(PG,S)=fWT(PG|PG,Ref)CWTReffcfs(S)
(9)
式(9)中:CO&M,base(PG,S)表示的是运行与维护成本(不包括运输的成本);fWT(PG|PG,Ref)是风力机尺寸系数;CWTRef是在理想条件下运行的额定功率为PG,Ref,风力机容量因数等于1的参考风力机的年度运行维护成本;fc是感兴趣地点的虚拟孤立风力机的风力机容量系数;fs(S)是考虑风电场负荷水平和风力机间距对运行和维护成本影响的负荷系数。负荷系数取决于特定风电场风力机的负荷条件,并表示为风电场拓扑结构(间距):
(10)
式(10)中:PS,y是相关现场单独风力机的平均年发电量,PWF,y是风电场风力机的平均年发电量,PG是风电场中风力机的额定功率。
经过BERGER[11]的启发,每MW的年运营成本降低了14%。本文假设这种相对减少可以线性地外推到风力机规模范围内的其他风力机规模范围,因此,对于风力机尺寸规模的增加,风力机尺寸系数量化如下:
fWT(PG|PG,Ref)=
(11)
对于风力机尺寸规模的减少,风力机尺寸系数量化如式(12):
fWT(PG|PG,Ref)=
(12)
其中,上述线性表达式中因子的差异与参考风力机在这些表达式中分别是最小和最大的风力机有关。
据文献[7]作为目前研究的参考风力机是为一个10 MW的风力机,其运行维护(OM)成本每年可指定为CWTRef= 106 EUR/kW。然而,到海岸的距离也是一个额外的重要参数,因此,为了确定实际的运行维护费用,公式(6)需要加一项修正,该项取决于到海岸的距离。所以完整的运行维护成本如下:
CO&M(PG,S,γ)=CO&M,base(PG,S)+CO&M,L(γ)
(13)
式(13)中:CO&M,L(γ)是与运营和维护(OM)相关的运输成本,其中的γ是风电场到岸边的平均距离。在一阶近似下,确定距离相关参数的简单方法假设一个线性关系,反映运输时间与船舶燃料消耗的比率:
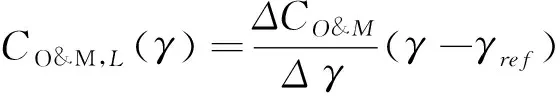
(14)
式(14)中:γref是参考距离(定义为20 km),γ是风电场到岸边的平均距离。

(15)
式(15)中:汇率为1 EUR(欧元)=7.50 DKK(丹麦克朗)。假设平均利润率为13%,上述估计值的87%应用于弥补运营和管理费用之间的差额。如果进一步引入风电场容量系数fWF,得出OM成本与海岸距离的关系:
CO&M,L(γ)=0.87×0.814×10-3×8 760×fWF(γ-γref)=6.2fWF(γ-γref)
(16)
式(16)中:8 760fWF是风电场中风力机的一年满载小时数,由于方程(12)是线性的,仅基于两个“观测”,因此它不适用于距离海岸线更远的分析距离。因此,在本文中,使用的风电场仅距海岸35 km。
1.3 土地征用费用
当建造风电场后,风电场所占地区就不可以用作他用。所以所占地区的费用不可能是免费的,哪怕是海上风电场也需要考虑土地征用费用。具体土地费用如下:
CF=cf×AF
(17)
式(17)中:cf为单位面积的土地征用费,EUR/m2;AF为风电场占地面积,m2。
1.4 风电场度电成本(LCOE)计算
综合上述风电场年发电量与风力机成本模型计算,最终估算出风电场的度电成本(LCOE)计算公式定义为资本支出加上运行维护(OM)成本除以总产量,如式(18)所示:
LCOE=
(18)
式(18)中:NY是风电场的寿命(一般假设为20年);PE是风电场的年发电量,kW·h。
2 发电功率计算
2.1 风电场信息
本文采用的海上风电场面积为3 200 m×3 200 m。风电场平均水深为10 m,平均离岸距离为35 km。风电场中风力机的型号为Vestas V80 2 MW, 切入/切出风速为3/25 m/s。海上风电场占地费用为1.2 EUR/m2。
2.2 年发电量AEP计算
1)尾流模型
本文所使用的尾流模型为2D Jensen尾流模型,公式如式(19)~式(20)。
预测步:u*=u0[1-2a/(1+kx/r1)2]
(19)
校正步:u=(u0-u*)cos(πr/rx+π))+u*
(20)

2)风资源
风电场的风资源主要采用文献[12]中的风玫瑰图和威布尔分布。可采用数学模型的威布尔密度函数描述各大小风速的频率分布情况,威布尔函数表达式为:
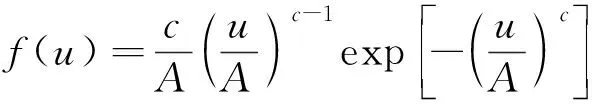
(21)
概率分布函数为:
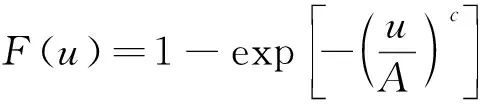
(22)
根据威布尔分布所给出的参数A、c及概率分布函数可以得出每一个风速出现的概率。公式如式(23):
(23)
式(23)中:A为缩放参数,m/s;c为形状因子,v(i)为风速范围为切入到切出的风速。所以风电场的年发电量可通过上述公式并考虑混合尾流和偏尾流效应算出每一台的入流风速,从而插值出风力机功率,并考虑风速出现的概率和风向,最终算出如下:
(24)
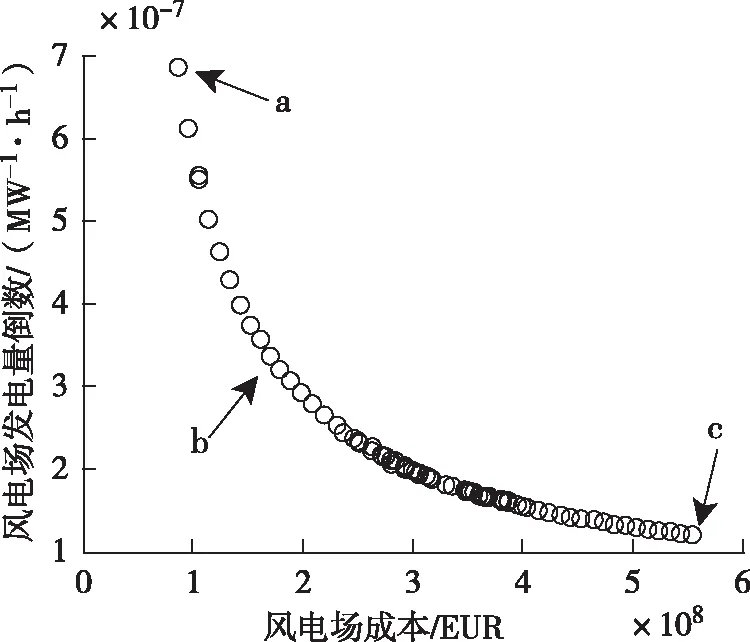
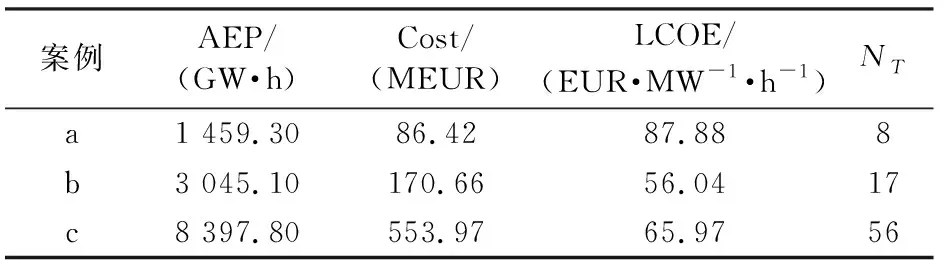
式(24)中:Nt为风力机的台数;dir为风向;8 760为风电场理想运行小时数;N代表将入流风速一共分为45段,v=3∶0.5∶25;P代表风速为v(i)时风力机功率;f代表风速在v(i) 本文研究的主要是在平坦地形海上风电场经济成本预测模型与管理优化研究,同时假设风电场面积有限,在已有的风资源数据和风力机型号下。本文中的目标主要是风电场的的经济成本和发电功率。研究中具体的变量与目标如下: 变量1:风电场内风力机组总个数Nt; 变量2:风电场中风力机的安装位置; 目标1:较低的经济成本Ctotal; 目标2:较高的发电量Ptotal。 其中:Ctotal是风电场总的投资成本(20年的运维成本与风电场土地征用费);Ptotal是20年的发电量总和。 1)优化算法 本文采用的优化算法主要是遗传算法[13](Genatic Algorithm,GA),它是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是通过模拟自然进化过程寻求最优解的方法。由于遗传算法具有思想简单、易于实现和应用效果明显等优点在众多领域得到广泛使用。 2)优化策略 本文优化策略为:首先采用N×N个网格来将风电场离散为N2个小网格组成,此时每个网格的面积为(5D)2即0.16 km2。假设风力机被安装在网格中心,使用字符“1”来代表网格中有风力机,字符“0”代表网格中无风力机。这样风电场中风力机的安装位置就可以通过由字符“0”与字符“1”组成的字符串来表示出来。风电场优化策略示意图如图1所示。 图1 风电场优化策略示意图 将这些初始个体形成初始群体,之后在对这些群体进行选择、交叉和变异等一系列操作。形成一个新的字符串,从而形成新的风力机坐标。将之代入年发电量和经济成本中,得出一次的结果。并在此结果的基础上不断优化下去,优化到规定的代数后结束优化。之后将这些结果输出,并从中寻到最优解。其中,迭代次数设为150;种群数设为50;优化变量个数为64;在设置出对应的交叉概率,变异概率;并规定变量约束最小值,变量约束最大值。 图2 风电场布局优化流程图 在变风速变风向情况下,以经济成本和发电功率为优化目标,得到的风电场布局优化结果如图3所示。图中x坐标为风电场的经济成本(EUR),y坐标为风电场的20年的发电功率的倒数(MW-1·h-1)。同时在图3中分别取三个结果:(a)风电场经济成本最小;(b)风电场度电成本最小;(c)风电场发电量最大。具体发电功率和经济成本如表1所示,各结果处风力机布局分别如图4所示。图4(a)、(b)中可以看出风力机主要大概是沿着两对角线分布的,因为风向角在210°到270°、270°到330°区间内的风频率概率是相对较大的,而沿两对角线分布可以很好的垂直于风速方向,这样可以最大程度上避免尾流效应的干扰,达到最大利用风资源的目的。同时发现最优度电成本情况下的风电场建设,并不需要过多的风力机组数,需要综合考虑布局和入流风资源即可。图4(c)是风电场最大发电量时结果,但是只考虑了发电量,并没考虑经济成本,不适合使用。 图3 风电场布局优化结果 图4 各结果处风力机分布图 表1 发电功率和经济成本 其中,通过表1可获得对于优化的风电场最适合的经济成本是控制在170.66 MEUR,风电场投资17台风力机为最优成本管理策略方式。表2为优化策略三种方案的风电场经济成本分布数据。从表中可以看出海上风电场经济成本中运维成本最多,虽然占总成本接近50%,但是随着风力机的台数增加,运维成本所占比例变化并不大,可见风力机台数增加对于风电场成本的管理更合理;其次成本占比较大的为风力机组的购买成本,约占20%左右。根据度电成本的最优,可获得较优的风力机组成本应该控制在35 MEUR左右,运维成本控制在89 MEUR左右。 表2 风电场经济成本分布数据 MEUR 本论文根据风电场建设和运维所需的成本,建立了各部分成本的数学模型,实现了风电场经济成本预测;然后结合工程尾流模型,计算出风电场年发电量,获得了度电成本;最后根据遗传优化算法,模拟研究了风电场布局管理和成本管理方式。根据风电场度电成本最小得出各个经济成本占比分别约为:风力机组21%、支撑结构7%、电网成本2.5%、额外成本10%、运维成本52.5%、土地征用7%。针对三种优化目标对比分析得出风电场同时考虑经济成本和发电总量较为合理,并且获得了经济成本分布方式,其中较合理的风力机组和运维成本占主导地位,分别为35.91 MEUR和89.70 MEUR,其中运维成本控制随着风力机数量增加更合理;同时整个风电场布局分配管理,除了考虑成本之外,风资源影响到发电总功率,因此建设风电场的经济成本规划受到风资源影响也较大。3 成本管理策略优化
3.1 变量与目标函数
3.2 优化算法及策略
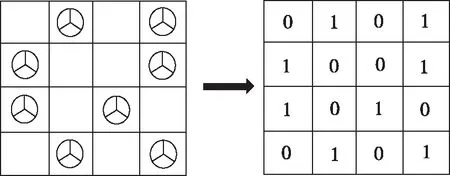

3.3 优化结果及分析


4 结语

