基于MOEA/D-DAE的轨道车辆扇形压电元件结构优化方法

孙佳慧，钟倩文，郑树彬，彭乐乐，文静

(上海工程技术大学 城市轨道交通学院，上海 201620)

随着我国轨道交通线网规模的不断扩大，以车载传感器为节点，实现车辆运行过程中的在线健康状态监测和管理成为目前的主要发展趋势[1]。传统的车载传感器依赖于外部有线电源或电池供电，极易在持续的振动冲击和电化学反应中受到损坏，严重威胁乘客出行及设备运行安全，对轨道交通的运维工作提出了巨大的挑战。而对小功率传感器进行无源无线化设计可以减少电池的使用、避免复杂的外部线路。基于此，在相关领域已经涌现出了丰富的研究成果，其中最受关注的技术是压电振动能量收集(vibration energy harvesting, PEH)[2]，PEH 技术可以利用压电效应从环境振动中俘取能量。为用电器供电的器件叫做压电俘能器或者压电能量收集器，通常与传感器结合起到自供电作用，形态多为梁式结构。近年来的相关成果主要有：ZHU 等[3]提出了一种由压电-摩擦能量收集单元组成的d-拱形自供电无线振动传感器，经过对表面俘能结构的尺寸优化，输出电压和电流分别提高了25%和42.6%。ZHANG等[4]开发了一种具有自供电状态监测能力的滚动轴承压电俘能器，建立输出电压模型用于优化。NABAVI 等[5]以有限元模型训练深度神经网络，用遗传算法对双夹蛇形宽频压电梁的输出功率进行了优化。KIM 等[6]通过有限元模型建立了多层悬臂梁的Kriging 模型，敏感度分析优化得到最优的结构参数。张琛等[7]根据变压器的振动特性，设计了一种多模态三悬臂式压电俘能器，实现了振动传感器的自供电。黄如艳等[8]为解决车载微型传感器自驱动化问题，分析了结构参数对于双端固支压电梁输出功率的影响，并进行了优化设计。傅成城等[9]采用有限元接触工具和网格分布分析的整体仿真接触面优化方法，提出了压电振动传感器的固有频率优化设计方案。王乐生等[10]通过仿真模型，研究了6种不同形状单悬臂压电梁的电压输出情况，为优化设计提供理论支撑。综上所述，PEH技术可以将轨道交通中丰富的振动能量回收再利用[11]，能量来源稳定，具有结构简单、功率密度高、可扩展性好等优点，且性能受到结构参数的影响，可以通过建立理论模型或有限元模型进行分析。但仍存在以下不足：1) 目前的文献大多数直接对输出功率、电压等输出量直接进行优化，对压电元件的工作频率和振源频率进行匹配[4]，以优化能量获取效率的研究较少。2) 已有文献缺乏对于俘能器与轨道车辆某子系统实际振动特性的适应性的研究。3) 优化设计采用的方法种类繁多，大多数对参数和目标输出量之间的关系进行讨论，建模求解过程耗费成本较高，难以对优化对象在多维空间内的问题全貌有整体性的了解。4)优化方法缺乏整体性，建模分析与优化过程较为分散，准确性还有提升空间。基于此，本文对一种扇形压电梁元件组成的阵列式俘能器基本结构进行研究，建立了精确度较高的Kriging 代理模型；获取了实际轨道车辆轴箱处固有的频域振动特性；以压电梁的工作频率点与轴箱振动频率集中点的距离、结构自重最小构建多目标优化模型，提出了轨道车辆扇形压电元件结构参数优化方法用于求解，在计算速度和准确性方面相比于其他算法具有显著优势。

1 扇形压电悬臂梁结构建模

1.1 悬臂梁物理结构

压电梁元件能够将车辆运行条件下产生的振动机械能通过正压电效应转换为电能，多个具有不同工作频率的扇形压电梁组成的阵列式俘能器，可以分别匹配多个振源频率，以达到整体宽频响应的效果[12]。压电材料为PZT-5H，金属基底材料为铍青铜，末端质量块为密度较大的黄铜，具体的结构参数和材料参数分别见表1和表2。

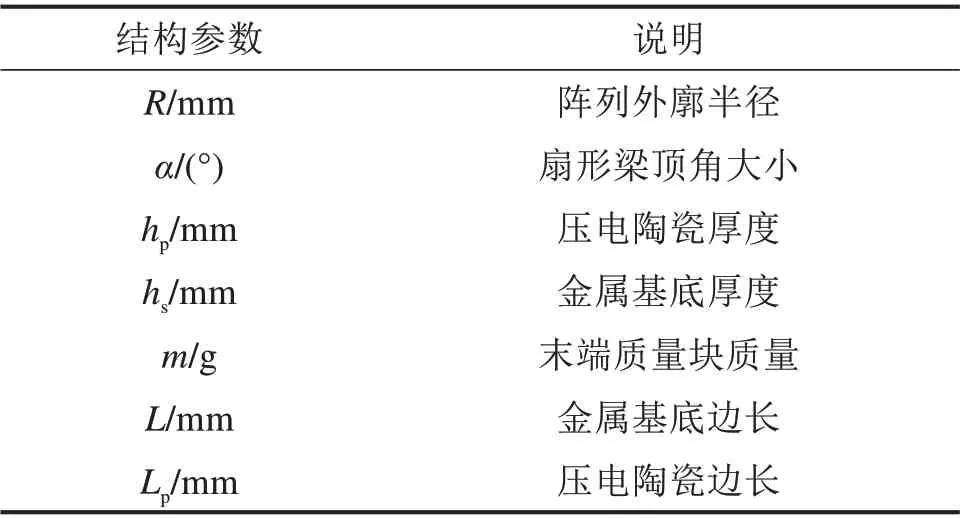
表1 主要结构参数Table 1 Structual parameters

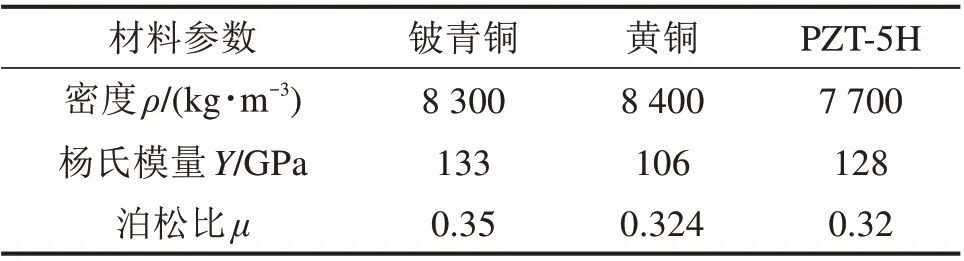
表2 材料参数Table 2 Material parameters

图1为俘能器结构图。其中，阵列结构如图1(a)所示，N个扇形悬臂梁增加了能量收集单位，对每个梁的结构参数分别进行最优化设计；扇形压电梁结构如图1(b)所示，2 片尺寸相同的压电陶瓷及质量块由环氧树脂固结在金属基板的上下表面，金属圆弧边伸出部分被压环夹紧固定。

1.2 悬臂梁理论及仿真建模

根据厄尔图克等[13]的悬臂梁分布参数机电建模理论，短路条件下r阶无阻尼固有频率fr：

其中：λr为质量归一化函数特征值；YI为短路条件下复合变截面的弯曲刚度；m为截面单位质量。

系统的稳态电压频率响应为：

系统的功率的频率响应函数为：

其中：θr为模态机电耦合项；δr为模态力学参数；ζr为r阶模态对应的阻尼比；Ceq为等效电容；Rt为负载电阻；G为基础平动位移的幅值大小。

由分布参数模型可得扇形悬臂梁单元的1阶模态频率与电压、负载电阻之间的变化关系如图2所示。从图2(a)可以看出，随着负载电阻从0～4×105Ω逐渐增加，悬臂梁单元的输出电压逐渐增大直至趋于稳定，稳定值近似等于开路电压。从图2(b)可知，输出功率随负载的增加，呈现先增大后减小的趋势，存在最优负载。

为获得在不同采样点处梁的模态频率和质量以生成初始的样本种群，本文使用ANSYS 有限元分析软件，在Mechnical APDL 19.1 环境中建立参数化的有限元模型：在该模型中，弧形端设置为固定约束，使用等电位耦合来约束陶瓷和基板之间的电行为；基底部分为一个具有密度、杨氏模量和泊松比等材料特性的薄板，压电层由具有电学特性的耦合场体单元组成。将6个主要结构参数定义为变量x1～x6，并赋初值，依据实际安装传感器的安全空间，以初始设计的上下80%作为参数设计范围的上下限，对应关系见表3。

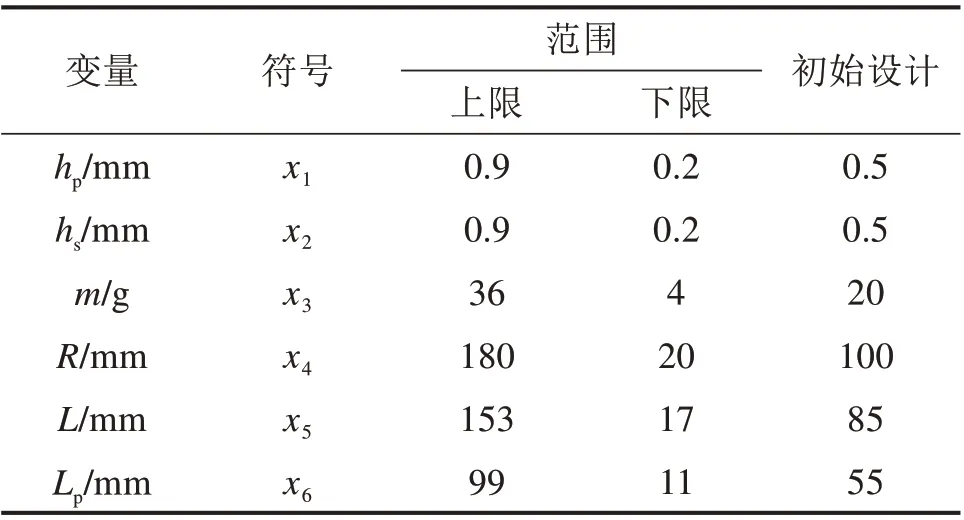
表3 结构参数的变量定义及初值Table 3 Variable definition and initial value of parameters

相关研究表明，列车运行时轮轨传递到车辆子系统中主要为中低频能量[14]，因此在设计的时候，主要考虑低频响应部分。对有限元模型进行模态分析，如图3 为扇形悬臂梁的前6 阶振动模态振型：1阶和2阶模态的自由端在垂直方向上运动，与压电材料的极化方向重合，应变分布在悬臂梁上；在设计范围内，第3阶及以上模态频率普遍较高，难以与车辆系统获得的低频能量发生共振。因此选择扇形悬臂梁的1 阶、2 阶垂向弯曲模态作为待设计的工作模态，与轨道车辆振动频率进行匹配，使得压电俘能器在列车在正常行驶过程中尽可能处于共振状态，进而提高其供电能力。在保证其他参数优化的同时，为了便于安装的目的，质量优化也需考虑在内。

本文在上海地铁某线采集列车振动信号，设备安装及测试结果如图4所示。固定架安装在列车轴端，图4(a)中螺栓固定的三轴加速度传感器通过采集线将振动信号数据传输到图4(b)列车车厢的信号采集仪。测得的时速50 km/h 以内车辆振动信号的振动频率主要分布在20 Hz 和200 Hz 附近区域，不随运行速度发生变化，频谱及时域谱详见图4(c)和4(d)。根据该振动特征可以进一步确定频率匹配的目标。

2 多目标优化问题及求解

2.1 问题描述

本文选取1 阶模态频率f1与目标频率fa之间的差值F1，2 阶模态频率f2与目标频率fb之间的差值F2和总质量FM作为目标函数。压电陶瓷厚度hp，金属基底厚度hs，末端质量块质量m，阵列外廓半径R，金属基底长度L和压电陶瓷长度Lp作为设计变量，具体的变量定义在表3中已经给出。多目标优化模型：

其中X={x1，x2，x3，x4，x5，x6}为变量的集合。

对于这种多变量多目标优化问题，传统的基于梯度的优化方法由于容易陷入局部最优，一些常用的基于Pareto支配关系进行选择的优化算法又存在计算复杂度高、速度缓慢等问题。针对这些缺陷，本文提出了一种Kriging 代理模型辅助的MOEA/D-DAE 优化方法，其优点在于：1) 将有限元模型转化为反映变量与输出之间精确关系的Kriging 代理模型[15]，是现有代理模型中拟合精度最高的一种，从建模方面大大节约了计算成本。2) MOEA/D-DAE 算法是近年来提出的一种基于分解的多目标进化优化算法[16]，其特有的检测-逃逸判断策略使得它不易陷入局部最优，且收敛速度更快，计算复杂度更低，可以从算法方面提高性能。

2.2 Kriging模型及其验证

代理模型能够将实际问题转化为多维空间内的高精度的数值优化问题，在空间内拟合样本点，生成的模型可以对连续设计空间中任意点的目标响应值进行预测，充分发挥计算机辅助设计的优越性。相比于其他常用的响应面模型、径向基函数模型等，Kriging 模型基于最小化期望平方误差原理，预测精度最高[17]。

首先，使用拉丁超立方采样法(Latin Hypercube Sampling, LHS)[18]进行试验设计，采集多维设计空间中有限个均匀分布的样本点集X={x1，x2，…，x6}n，输入到有限元参数化模型中获得其对应的响应值集合y={y1，y2，…，yn}n，X和y合并为完整的样本种群，用于训练Kriging 模型。样本点集的大小和变量个数之间的关系为：

式中：n表示变量个数，取n=6；k表示模型的样本点数。

采样和代理模型的构建借助ooDACE Toolbox[19]在Matlab R2018a环境下编程实现，拟合采样点分布情况及拟合的Kriging 高精度模型以图5 所示为例：采集的样本在多维空间内均匀分布，目标FM的代理模型在约束下采样点分布较少的区域及边缘部分误差较大，在设计空间内的拟合情况较好，因此需要增加样本点对模型进行修正，直到其满足精度要求。

图6 中选出了3 组关系，在三维空间内对于单个目标，存在最优值。由图6(a)可知优化目标F1与hp正相关，这表明在后续的优化过程中可能会呈现向下收敛的趋势。如图6(b)，Lp和L对于目标F2在求解过程中有陷入局部最优解的风险。

参考相关研究中对代理模型的评价方法[20]，使用交叉验证方法分别计算模型的回归评价指标，取一组测试数据和测试数据所在位置的样本点，计算模型评价指标R2和相对方均根误差RMSE，RMSE 越小，R2越接近1，模型精确度越高。最终评价指标F1模型的R2为0.803，RMSE为0.103；F2模型的R2为0.853，RMSE为0.073。

2.3 MOEA/D-DAE算法优化求解

本文采用的代理模型辅助的MOEA/D-DAE 算法的基本流程如图7 所示，包括前述的试验设计、代理模型建立、多目标优化求解过程，最终可获得Pareto 前沿和相应的Pareto 集，属于一种改进的ε约束处理方法，可以提高解的多样性。在进化过程中，它会在检测到局部最优时启动DAE(Detect and Escape)过程，以最大程度避免陷入局部最优。

算法在PlatEMO 平台[21]实现。最终得到的Pareto 前沿如图8 所示，优化给出了3 个目标函数的最优Pareto集和前沿上的解对应的仿真模型的形态。在相同种群设置下，MOEA/D-DAE 仅耗时10 865.49 s， 而 常 用 的NSGA-II 算 法 耗 时13 139.88 s。

2.4 解集聚类分析

可行的最优解均匀分布在Pereto前沿上，为此使用聚合树(Aggregation Tree, AT)方法[22]分析最优解集的特征，并选择最终解。2 个目标越和谐，就越适合将它们缩减或分组为一个新的标量化目标值，树可以显示相互冲突的目标之间的关系。

生成的聚合树和极坐标权衡图如图9所示。有3 个叶子节点，分别代表3 个目标F1，F2，FM，叶节点的父节点表示由目标和值的重新正规化组成的复合目标。3 个目标之间的冲突率为99.52%，F1，F2之间的局部冲突水平较低。树的分支大小与它的冲突成比例。目标相距的越远，不和谐程度越高，由此可知，3 个目标之间确实存在互相冲突的关系，需要选择一个折中方案。

从图9 所示的类别中选择3 个最优解：解SA，解SB 和解SC，和参考的最小质量解Ge、全局均衡解Mm。获得的FEM 响应如表4所示，相比于初始解，解SA 和SB 在频率上与轨道列车轴箱频率集中点更匹配。

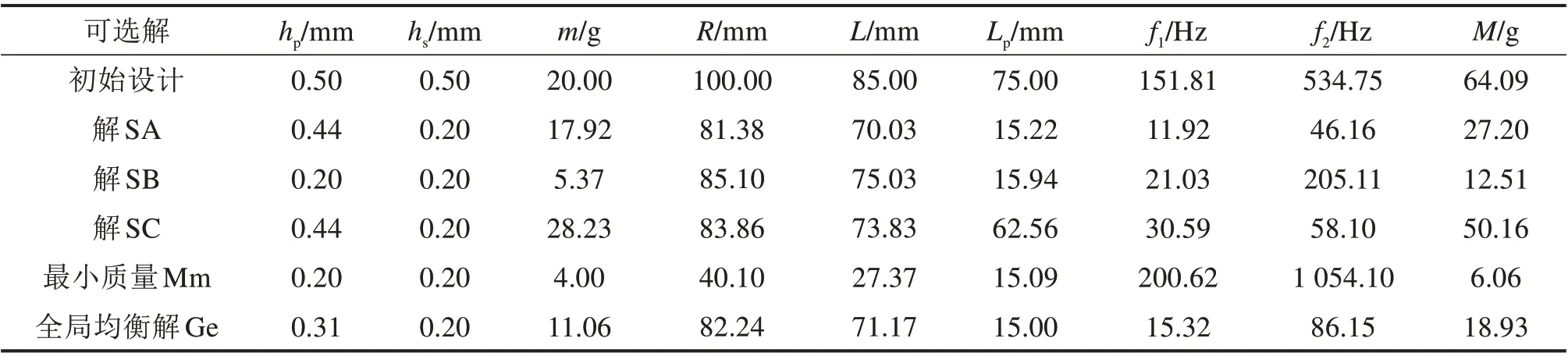
表4 拟选最优解的设计目标值Table 4 Design target value of the proposed solution

3 结果分析

为了验证本文所建立的优化设计方法的准确性，采用有限元法对选择的解进行了验证。图10为谐响应分析得到的所有选择的解的频率-电压响应曲线，表5 为谐响应分析得到的1 阶模态和2 阶模态对应电压以及计算得到的最优负载和理论最大输出功率，输出电压最高提升至初始设计的219%，解SA 对应的理论最大输出功率达到0.33 W，相比于初始设计提高了0.28 W，所有解的工作频率与环境振动频率匹配程度均得到了增强。分析结果表明，优化设计方法得到的输出结果相对于初始设计普遍得到了显著提升。

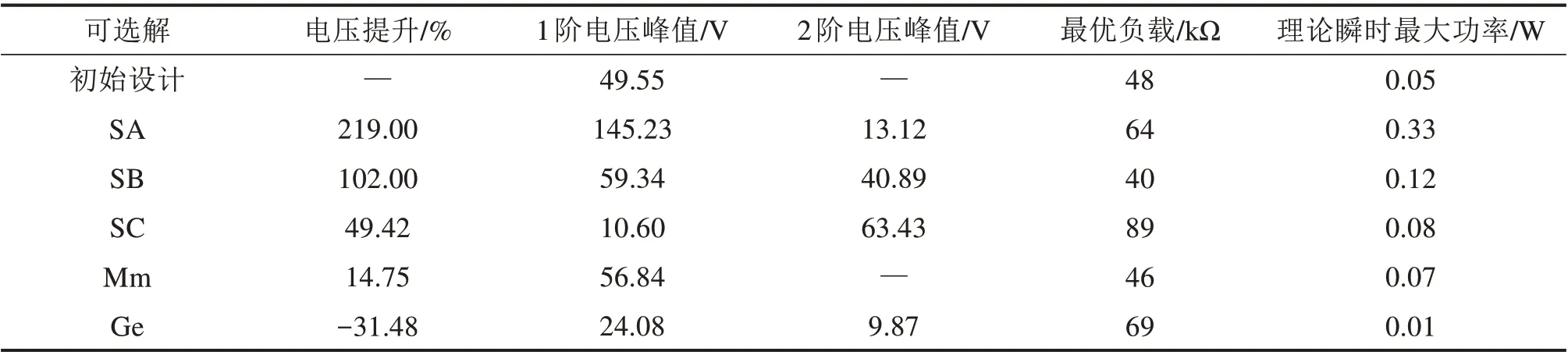
表5 最优解的输出性能值Table 5 Output performance value of the solution

4 结论

1) 对一种压电圆盘阵列式扇形悬臂梁俘能器结构参数进行优化。选择1 阶模态频率、2 阶模态频率和梁总质量为优化对象，给出设计变量的设计边界，建立压电梁悬臂的多目标优化模型。

2) 基于该优化模型，采用一种结合了代理模型技术的MOEA/D-DAE 算法的高效优化设计方法，将代理模型加入到优化过程中，极大地降低了计算成本。

3) 得到了均匀的Pareto前沿，用聚合树进行聚类分析解集特性，获得最终设计。得到变量和优化目标之间的相关关系，这对于进一步调整设计具有参考意义。

4) 结果表明，优化设计方法得到的输出结果相对于初始设计普遍得到了显著提升。1 阶电压水平最高提升至初始设计的219%，解SA 对应的理论最大输出功率达到0.33 W，相比于初始设计提高了0.28 W，所有解的工作频率与环境振动频率匹配效果均得到了显著提升。