近断层长周期地震波对桥台-引桥-刚构连续梁结构体系地震响应的影响

魏俊杰，张超，邬晓光，张文韬

(1. 武汉大学 土木建筑工程学院，湖北 武汉 430072；2. 长安大学 公路学院，陕西 西安 710054)

在历次地震中桥梁主梁之间以及主梁和桥台间的碰撞现象十分常见，剧烈的碰撞容易引起墩梁间相对位移过大而造成主梁局部损伤甚至落梁[1-2]。三跨高低墩刚构-连续组合梁桥的矮墩处盆式橡胶支座屈后刚度几乎为零，地震时巨大的水平惯性力将由柔性刚构墩承担，造成柔性制动墩抗震问题突出，同时较大主梁水平位移使伸缩缝处碰撞效应显著[3]。研究表明长周期地震波广泛存在于近远场地震中，相较于普通地震波具有更剧烈的破坏性，是近断层桥梁在地震作用下倒塌和损毁的主要原因[4-6]。国内外学者针对碰撞对桥梁结构地震响应的影响开展了一系列研究。李建中等[7]针对西部山区典型非规则多跨连续梁桥进行了碰撞响应分析。邓育林等[8-11]均以西部山区高墩大跨连续刚构桥为研究背景，分析考虑了土-桥台-上部结构相互作用后碰撞对桥梁结构地震响应的影响。AMJADIAN 等[12]分析了碰撞对于曲线梁桥平面位移的影响，并进行了详细的参数分析。WIESER 等[13]通过振动台试验分析了碰撞对曲线梁桥的影响，并与直梁桥进行了对比分析。IJIMA 等[14]利用模型试验分析了碰撞对斜曲线梁桥的影响，并研究了斜曲线梁桥的防倒塌措施。焦驰宇等[15]利用振动台试验分析了碰撞对小半径曲线桥的影响。闫聚考等[16]通过振动台试验分析了大跨度悬索桥与引桥的碰撞效应。国巍等[17-18]分析了近断层地震波对高铁多跨简支梁桥的弹塑性反应影响。侯烈等[19]分析了近断层地震波脉冲效应对大跨结合梁斜拉桥地震响应的影响。因此，在近断层长周期地震波作用下，碰撞对桥梁结构地震响应影响的研究目前主要集中在连续梁、连续刚构、简支梁和三跨曲线梁等常规桥型，而针对三跨高低墩刚构-连续梁桥的研究则相对较少。本文以西宝高速改扩建中某三跨刚构-连续组合梁桥为研究对象，分析不同类型长周期地震波和脉冲型地震波脉冲周期对桥梁结构地震响应的影响。

1 工程概况

桥梁跨径布置为(3×20+65+120+65+3×20) m，桥梁全长370.5 m，主桥最大墩高54.95 m。主桥为预应力混凝土刚构-连续组合体系，由单箱单室箱形断面组成；下部主墩为单薄壁空心墩，桩基础；分割墩为双柱式墩，桩基础；引桥上部结构为3×20 m预应力混凝土先简支后连续小箱梁，由5片预制小箱梁通过横向联系拼接而成，下部为柱式墩、桩基础；两侧桥台均为肋板式桥台，桩基础。全桥跨径布置立面图如图1所示，从左往右的墩台编号依次为0 号台，1 号，2 号，3 号，4 号，5 号，6号，7 号，8 号墩和9 号台，墩高依次为5.5，6.0，10.5，54.95，10.05，6.0，6.0 和5.5 m。其中3 号和6号分隔墩处设置240型伸缩装置，0号和9号桥台处设置80 型伸缩装置。引桥在桥台、过渡墩处共设置10 个滑板式橡胶支座，型号GYZF4 d425×65；引桥中间墩各设置10 个板式橡胶支座，型号为GYZ d570×71；主桥在过渡墩处各设置2 个单向活动盆式支座，型号JPZ(KZ)7DX；3 号活动墩采用3 个单向活动盆式支座，型号为JPZ(KZ)30DX。墩台桩基均采用摩擦桩，桥台持力层为老黄土，其余桩基持力层为老黄土、粉质黏土、圆砾、细沙和卵石。车辆荷载等级按公路Ⅰ级进行设计。

2 有限元建模和边界条件模拟

运用有限元软件CSIBridge 建立主桥结构与引桥碰撞的弹塑性动力分析计算模型，沿纵桥向进行一致激励，且不考虑近断层地震波的竖向高频分量。主梁和桥墩采用梁单元，梁和墩柱的单元划分能够反映结构实际动力特性。承台和两侧桥台采用厚壳单元进行建模，采用纤维铰和P-M2-M3 铰分别模拟引桥桥墩和主桥桥墩可能出现的非线性行为，无约束混凝土和约束混凝土的材料特性基于Mander 模型[20]，二期铺装采用线质量。采用分层土弹簧模型对主引桥桩基的桩土相互作用进行模拟，土层m值按照规范[21]建议值取值，有限元模型见图2。板式、滑板式橡胶支座和盆式橡胶支座均按照《公路桥梁抗震设计规范》(JTG/T2231-01-2020)的建议采用理想弹塑性滞回曲线模拟。桥台与台后填土的接触关系采用Duncan-Chang 非线性本构关系定义的Multilinear Elastic Link单元进行模拟[22]，非线性本构关系式和计算结果如式(1)和图3所示。

式中：p为土体作用于台背的土压力；u为台背后土体的水平位移；Pult是作用于台背的被动土压力；K为初始刚度；Rf为经验系数，取0.8。其中，根据工程实际和《公路桥梁抗震设计规范》(JTG/T 2231-01-2020)可以计算出初始刚度K和被动土压力Pult。

本文采用文献[16]中组合Kelvin 碰撞单元模拟伸缩缝间的接触非线性，碰撞单元刚度根据王东升的建议取较短主梁轴向刚度值的0.5 倍[23]。伸缩缝处碰撞单元及其非线性力-位移关系分别如图4和式(2)所示：式中：Δ 为伸缩缝初始间隙，根据设计文件取主引桥间为0.19 m，引桥与桥台间为0.06 m；u1，u2分别为地震作用下伸缩缝处相邻梁体的位移；v为梁体碰撞时的相对速度；c为碰撞单元阻尼，本文取值为5。

3 桥墩截面分析

利用CSiBridge Section Designer 程序对各桥墩进行截面分析，计算各墩柱的屈服极限、强度极限、屈服曲率和极限曲率，为地震作用下结构的服役状态提供判别基准。同时，依据《公路桥梁抗震设计规范》JTG/T 2231-01-2020 分别计算各桥墩墩顶允许位移，计算结果如表1所示。

表1 截面分析数据Table 1 Cross-section analysis data

4 地震动特性分析

根据文献[24]中关于近断层地震的定义，选择Chi-Chi 地震中断层距60 km 以内的脉冲型地震波、类谐和地震波、长周期地震波和普通近场地震波共计123 条进行分析，计算卓越频率、PGA(峰值加速度)，PGV，PGD，PGV/PGA 和强震持时等地震动参数，结果如图5所示。结果表明：近断层脉冲型地震波具有较大地震动参数，其PGA，PGV和PGD 平均值分别是类谐和地震波、长周期地震波和普通地震波的2.9 倍、2.1 倍和1.3 倍；2.6 倍、3.3 倍和3.6 倍；3.4 倍、4.9 倍和8.6 倍。但脉冲型地震波的强震持时仅为上述3类地震波的的0.4倍、0.5 倍和0.7 倍。从图5(d)可以发现脉冲型、类谐和和长周期地震波的PGV/PGA 值更大，其均值分别为普通地震波的2.6 倍、2.6 倍和1.7 倍，说明长周期地震波与普通近场地震波在相同加速度时具有更大速度峰值和更强速度脉冲。从图5(f)可以发现：3 类近断层长周期地震波卓越频率均低于1 Hz，且远小于普通地震波卓越频率。

同时计算123条地震波的加速度反应谱、速度反应谱和位移反应谱，并进行平均化处理。由于具有相同的规律，此处仅列出加速度反应谱如图6所示。可以发现：近断层脉冲型地震波的反应谱值最大。普通近场地震波的反应谱值在0～1 s内均大于类谐和地震波和普通长周期地震波，在周期大于1 s 后最小，说明类谐和地震波和普通长周期地震波对特征周期大于1 s 的结构具有更大破坏作用，而普通近场地震波对于特征周期在0～1 s内的结构破坏性强。同时在0～2.5 s 内，普通长周期地震波的反应谱值大于类谐和地震波，在2.5～6 s 时则相反，原因可以解释为类谐和地震波的卓越频率较小，特征周期较长。

5 地震波类型对结构地震响应的影响

选择加速度峰值和卓越频率相近的4种类型地震波各3条进行纵桥向一致激励，取分析结果的平均值进行比较，地震动详细信息如表2 所示。图7给出了各桥墩在不同类型地震波作用下的墩顶位移、墩底弯矩、墩底剪力和伸缩缝碰撞力峰值对比，为了量化说明地震波类型对结构地震响应的影响，本节定义最大改变率i=(imax-imin)/imin，其中imax为最大响应值，imin为最小响应值。

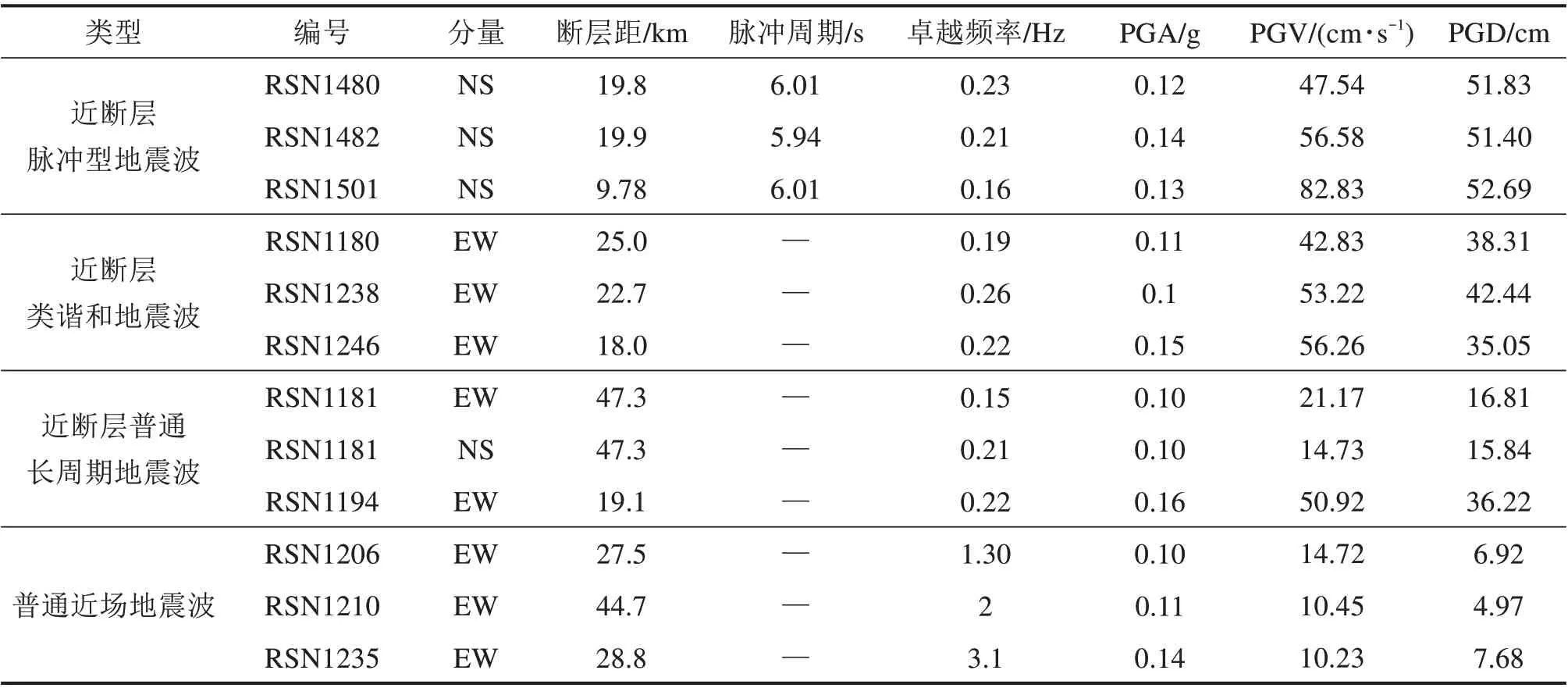
表2 地震动特性参数Table 2 Ground motion characteristic parameters

从图7(a)可以看出各伸缩缝碰撞力峰值在长周期地震波作用下显著增大，普通近场地震波作用下各伸缩缝均未发生碰撞，脉冲型地震作用下A-B缝碰撞力峰值相对长周期地震波和类谐和地震波最大改变率分别为99%和124%。图7(b)可以看出长周期地震波作用下各桥墩顶位移显著增大，脉冲型地震波、长周期地震波和类谐和地震波对各桥墩墩顶位移的改变率均大于450%，且对刚构墩顶位移影响最大，最大改变率分别为4 607%，3 869%和12 416%。长周期地震波显著增大了各桥墩墩底弯矩和剪力，脉冲型地震波、长周期地震波和类谐和地震波对桥墩墩底弯矩最大改变率分别为1 017%，865%和2 912%，对桥墩墩底剪力最大改变率分别为607%，543%和1 263%。同时不难发现：普通近场地震波作用下各桥墩均未发生屈服；长周期地震波和类谐和地震波作用下仅3号墩底发生屈服破坏；而脉冲型地震波作用下，1号，3 号，4 号和6 号桥墩底弯矩均大于等效屈服弯矩。图7(d)为刚构墩底纤维铰的弯曲-曲率滞回曲线，刚构墩墩底纤维铰在3类长周期地震波作用下已明显屈服，而在近场普通地震波作用下仍处于弹性状态，脉冲型地震波作用下纤维铰的弹塑性行为最明显。由图7(e)和7(f)可知：脉冲型地震动和长周期地震动作用下桥台位移分别为0.43 m和0.27 m，台后填土将会发生显著塑形变形；桥台桩基截面最大弯矩分别为5 900 kN·m和2 300 kN·m，在脉冲型地震波作用下会发生屈服破坏。

因此，不同地震波类型对结构地震响应的影响可以总结为：近断层脉冲型>近断层普通长周期>近断层类谐和地震波>普通近场地震波。在对桥梁进行抗震设计验算时必须根据桥址处实际情况进行地震波类型的选择。

6 脉冲周期对结构地震响应的影响

为分析脉冲型地震波脉冲周期对结构体系地震响应的影响，采用小波分析对脉冲周期大小进行识别，如图8 所示。选择Chi-Chi 地震中不同脉冲周期的地震波延顺桥向进行一致激励。同时，为避免地震动强度的影响，将各地震波峰值加速度统一调至0.4g，所选地震动记录详细信息如表3所示。

表3 地震动特性参数Table 3 Ground motion characteristic parameters

图9(a)表明各伸缩缝碰撞力峰值随地震波脉冲周期增大而增大，各伸缩缝碰撞力峰值最大改变率分别为351%，850%，417%和659%。图9(b)中各桥墩墩顶位移也随着脉冲周期增大呈逐渐增大趋势，1 号至8 号桥墩墩顶位移最大改变率分别为1 024%，968%，1 114%，1 649%，869%，288%，245%和179%。同时，脉冲周期增大也使得各桥墩墩底弯矩和剪力增大，1 号至8 号桥墩墩底剪力最大改变率分别为68%，91%，213%，262%，78%，216%，89%和76%；墩底弯矩最大改变率分别为152%，136%，247%，353%，121%，267%，86%和88%。其中3 号墩底在脉冲周期大于等于2.44 s后屈服，4 号刚构墩在脉冲周期大于等于8.69 s 后屈服，其余桥墩墩底弯矩随着脉冲周期增大而增大，但并未超过等效屈服弯矩。图9(e)和9(f)为左桥台位移时程曲线及其桥台桩基单桩弯矩包络图，脉冲周期增大使得桥台位移和桥台桩基截面弯矩也增大，在RSN1530 地震波(脉冲周期为8.69 s)作用下左桥台位移和桥台桩基截面弯矩分别为0.35 m和2 400 kN·m，将会使台后填土和桥台桩基发生较大塑形变形和屈服破坏，影响结构安全。

为了清晰表达脉冲周期的影响，选取RSN3475(1.02 s)，RSN1182(3.2 s)，RSN1503(5.74 s)和RSN1530(8.69 s)进行分析。图9(g)和9(h)为4 号刚构墩底纤维铰的弯矩-曲率滞回曲线和单根纤维的应力-应变曲线，4 号墩底纤维铰在RSN1182 地震波(脉冲周期为3.2 s)作用下已发生屈服破坏，单根纤维已发生塑形变形。随着地震波脉冲周期增大，纤维铰的塑性行为将更加明显，滞回曲线更加饱满并耗散更多能量。图9(i)为桥台A-B 缝处碰撞力时程曲线，可以明显看到脉冲周期越大，碰撞力峰值和碰撞次数都将会增大。

7 结论

1) 近断层长周期地震波参数(PGA，PGV，PGD)和反应谱值显著大于普通近场地震波，其中近断层脉冲型最大，类谐和地震波强震持时更长。因此在分析结构近场地震动响应时需考虑各类长周期地震波的影响。

2) 长周期地震波因其低频脉冲特性显著增大了桥墩的内力和变形以及伸缩缝处碰撞效应。其中近断层脉冲型地震波作用下，碰撞力以及各桥墩墩顶位移、墩底弯矩和剪力最大，主桥墩、过渡墩和台后填土会发生明显塑形变形，桥台桩基会发生屈服破坏。各类型地震波对结构地震响应影响的大小顺序依次为：近断层脉冲型>近断层普通长周期>近断层类谐和>近断层普通地震波。

3) 近断层脉冲型地震波脉冲周期越大，地震波具有的能量也将更大，导致结构地震响应也越大，仅3 号过渡墩和4 号刚构墩在脉冲周期分别大于2.44 s 和8.69 s 后发生屈服，其余桥墩均受力安全。但脉冲周期大于8.69 s 后，左右桥台桩基和台后填土将会分别发生屈服和显著塑性变形。建议在对实际工程结构进行地震响应分析时充分考虑长周期脉冲地震波及其脉冲周期的影响。