基于轻量时空图卷积模型的路网交通流预测

贺文武，裴博彧，毛国君，陈维亚

(1. 福建工程学院 计算机科学与数学学院，福建 福州 350118；2. 福建省大数据挖掘与应用重点实验室，福建 福州 350118；3. 中南大学 交通运输工程学院，湖南 长沙 410075)

交通流预测是智能交通系统的重要组成部分。一定精度的交通流预测能为交通疏导、车辆调度以及道路建设等提供决策依据，为物流、快递等运输行业提供规划指导，切实惠及人们的日常出行。为此，相关研究者持续努力，提出了多种交通流预测方法。早期方法如历史均值法(HA)，利用历史平均交通量来预测未来交通量，方法简单易行但不能有效捕捉交通流的动态变化[1]。基于统计方法的自回归综合移动平均(ARIMA)等也被应用于交通流预测[2]。此类模型易受到预测序列平稳性的影响，难以有效表征复杂的交通时序特征。机器学习方法具有高度的非线性学习能力，易于捕获交通流预测中所涉及的复杂关系。例如，经典机器学习方法k 近邻(KNN)[3]、支持向量回归(SVR)[4]等就被用于交通流预测。应用过程中，由于所涉交通路网通常十分复杂并天然具有时空依赖特性，相关研究者转向更具有复杂表征能力与端到端学习能力的深度学习方法和模型。例如，深度置信网络模型(DBN)[5]、堆叠降噪自编码器模型(SDAE)[6]等。此类方法没有考虑交通路网的空间特征或交通流的时序特征。卷积神经网络(CNN)最早被用来处理图像，MA 等[7]将城市路网划分为网格形式，基于卷积神经网络引入路网空间特征，在交通流预测上取得一定效果。然而，交通路网并非欧式空间结构，不具备普遍的平移不变性，此类方法在空间特征的提取上尚有改进空间。长短期记忆网络(LSTM)[8]、全连接长短期记忆网络(FC-LSTM)[9]以及双向长短期记忆网络(Bi-LSTM)[10]等模型也被用于交通流预测。总体上，此类模型未能充分发掘交通流预测中所涉及的拓扑空间特征。图神经网络能有效捕获拓扑空间结构特征，近期基于图神经网络的交通流预测受到相关研究者的关注。ZHAO 等[1]提出时间图卷积网络(TGCN)，将GCN[11]和门控循环单元(GRU)结合起来，组合成可提取交通网络时空特征的模型。YU 等[12]提出时空图卷积网络(STGCN)，该模型由2 个时空卷积块和1个输出块组成。相比以扩散卷积学习出空间表示和循环神经网络捕获时间特征的DCRNN模型[13]，STGCN 较大程度地降低了计算量。该模型中，时空卷积块使用单层GCN，而中长期的交通流预测中，各节点会受到较远距离的其他节点的影响，因此单层GCN 或不足以提取充分的空间特征，而简单增加层数又易于导致过平滑、计算量大等问题。与前述相关思路不同，ZHANG 等[14]提出结构学习卷积模型(SLCNN)，该模型在预测准确性上优于DCRNN 和STGCN，但其训练时长则远高于STGCN。高计算代价直接影响到交通流预测的响应时间，同时也增加了资源消耗。“双碳”目标下的绿色智能与计算具有多重意义。以适度的计算代价有效捕获时间与空间特征，准确预测交通流自然成为相关研究者的关注焦点。本文基于因果卷积与多层空间卷积构造“厚夹心”的单“三明治”式的时空卷积模块，简化预测模型结构的同时通过“厚夹心”引入多层空间卷积以捕获高阶邻居节点信息，设计递增丢边(DropEdge)策略消解高阶信息可能带来的过平滑风险，提出一种基于递增式丢边的轻量时空图卷积神经网络模型(Spatio-Temporal Graph Convolutional Network with Incremental DropEdge，IncDEST-GCN)，以期有效捕获交通流的时空特性，以更低的计算代价获得更高的预测精度。在基准交通数据集上充分实验，验证所拟方法与所建模型的有效性。

1 问题描述与基础模型

1.1 路网交通流预测

交通流预测涉及交通流量、交通速度以及交通密度等基本变量[15]，本文关注交通速度预测。路网交通流数据一般通过分布在路网上的多(N)个传感器(节点)所获取。本文以图G=(V，E)(其中V是N个节点的集合，E是节点之间连接边的集合)表征路网空间分布信息，并定义特征矩阵Xt∈RN×p，表示N个节点上t时刻的交通流特征信息。每个节点实际包含t时刻及前p-1 个时刻的交通流速度信息，即Xt=(xt-p+1，…，xt-1，xt)，xt∈RN×1为路网N个节点上t时刻的交通流速度。

据上所述，路网交通流预测可表示为基于路网结构G及其各节点上p个时刻的速度信息来学习未来q个时刻的速度信息，其间关系可用映射f(·)表示。具体如式(1)所示：

1.2 图卷积

针对模型(1)，本文以图卷积为基础构建预测模型f(·)，其卷积操作如式(2)所示：

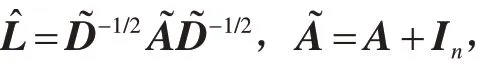
为丰富其表征能力，基于模型(2)引入神经网络激活层并构建多层模型，具体如式(3)所示：

其中：H(l)是第l层中的激活矩阵；H(0)=X，σ(·)是激活函数；W(l)是可学习权重(对应前文θ)。

1.3 因果卷积(Causal Convolution)

基于模型(3)，考虑交通流信息时序属性的有效提取，引入因果卷积，通过卷积核大小、层数与扩张系数等灵活控制感受野大小，捕获长程时间依赖关系。其示意如图1所示。

本文综合考虑交通流预测中的时空交互特性，以图卷积模型为基础，结合因果卷积构造紧凑、轻量的时空卷积模块，有效提取路网交通流时空特征，以更低的计算代价实现路网交通流的高精度预测。

2 基于递增式丢边的轻量时空图神经网络模型

2.1 IncDEST-GCN网络模型

轻量时空图卷积神经网络模型总体框架如图2所示。模型具体由一个时空卷积块与一个输出块组成(如图2(a)所示)。

时空卷积块(如图2(b)所示)采用“时间门控卷积+空间图卷积+时间门控卷积”组成的“厚夹心”单“三明治”式结构。其中，“厚夹心”空间图卷积采用多层GCN，捕获高阶邻居节点信息。其间引入递增式丢边策略减少活跃参数、消解过平滑。2 层时间门控卷积则分别捕获纯时间特征信息以及时空交互后的时间特征信息。

时间门控卷积(如图2(c)所示)采用简洁的门控线性单元(GLU)结构。单元以因果卷积为核心，并将通道数一分为二，其中一侧通过Sigmoid(·)函数捕获特征的非线性性，另一侧直接输出因果卷积结果并引入残差连接以防止特征丢失，最后通过哈达玛积(Hadamard product)汇聚两路特征。

输出块(如图2(d)所示)由一个时间门控卷积和2 个全连接层组成。其中，时间门控卷积聚合上游特征信息，将时间帧数缩减为1；第一个全连接层采用Sigmoid(·)激活函数捕获非线性，后一个全连接层聚合多通道特征信息，输出预测信息。

2.2 递增式丢边

交通流预测中路网空间拓扑结构以当前关注节点为中心呈“同心圆”向外扩展(如图3 所示)。由图3可见，随邻居节点阶数增加，空间感受野随之增加，但多层GCN 的过平滑风险也随之增加。递增式丢边策略以递增方式设置丢边比例，即随邻居节点阶数增加，丢边比例增加，渐进地稀疏化高阶邻居节点与当前节点的连接性，充分捕获高阶空间信息的基础上有效抑制过平滑所致的节点特征失效。图3 中，节点i的1 阶邻居节点有4个；2 阶邻居节点有6 个；3 阶邻居节点有11 个。随邻居节点阶数增加，中心节点感受野随之增加，高阶邻居节点对中心节点的影响则相对趋小。图中单实线(1 条)表示对1 阶邻居的丢边；双虚线(3条)表示对2 阶邻居的丢边；双实线(7 条)表示对3阶邻居的丢边。不难发现，递增式丢边能有效调节远近邻居对中心节点影响。

2.3 时空交互轻量化

图2(b)所示时空卷积组件中，为充分捕获时序特征，时间卷积通道数数倍于空间通道数(64∶16)，因此时间卷积与空间卷积的交互环节所耗计算资源大。第1 层GCN 各节点上需要聚合处理64个通道上的节点特征，第2 层GCN 则仅需聚合处理16个通道上的节点特征。因此，“厚夹心”的单“三明治”结构相较单层GCN“夹心”的多层“三明治”结构，更为紧凑、轻量，所涉计算代价更低。本文实验也表明“厚夹心”中的多层GCN 可有效捕获高阶邻居节点信息，能基于递增式丢边以更低的计算代价取得更高的预测精度。

3 实验设计与结果分析

3.1 基准数据集

实验采用基准交通数据集PEMSD7-S 与PEMS-BAY[14]，具体信息如下：

1) PEMSD7-S：包含自2012 年5 月1 日至6 月30日全部工作日的相关交通流信息，本文选取228个传感器节点信息，采集时间间隔为5 min。

2) PEMS-BAY：包含自2017年1月1日至2017年6 月30 日全部工作日的相关信息。本文选取湾区325个传感器节点信息，时间间隔为5 min。

实验采用Z-Score 方法对交通流数据统一进行标准化，并按照70%，10%与20%的比例将数据集划分为训练集、验证集与测试集。

3.2 实验设置

3.2.1 评价指标

同文献[13]，实验选取平均绝对误差(MAE)、均方根误差(RMSE)与平均绝对百分比误差(MAPE)3个评价指标。其具体计算公式略。

3.2.2 基线模型

所建模型将与下述基线模型[14]进行比较：1) 历史平均(HA)；2) 自回归综合移动平均(ARIMA)；3) 支持向量机回归(SVR)；4) 前馈神经网络(FNN)；5) 全连接LSTM(FC-LSTM)；6) 扩散卷积递归神经网络(DCRNN)；7) 时空图卷积网络(STGCN)；8) 结构学习卷积神经网络(SLCNN)。

3.2.3 参数设置

实验基于前60 min 的交通流速信息(p=12)分别预测未来15 min(q=3)，30 min(q=6)，45 min(q=9)和60 min(q=12)的交通流速。

时空卷积块中2 个时间门控卷积通道数为64，卷积核大小为(3,1)；空间图卷积通道数为16，4 层GCN，递增式丢边比例依次为0.2，0.3，0.4 和0.5；在1 和3 层使用丢弃法(Dropout)[16]随机掩蔽部分神经元消解多层图卷积网络潜在的过拟合风险，比例依通例取0.5；输出块中，时间门控卷积通道数为128，卷积核大小为(8,1)，2 个全连接层神经元个数分别为128 和1。模型以最小化平均绝对误差(MAE)为目标，采用AdamW 优化器，批量大小为64，训练100个Epoch。

引入动态学习率[17]，每间隔step_size 个历元更新一次初始学习率，其更新过程如式(4)所示：

其中：new_lrepoch为第epoch 个历元的初始学习率，initial_lr 为第一历元的初始学习率，γ为更新因子，epoch 为历元次数，表示向下取整，step_size 为更新步长。实验中，相关参数设置为：initial_lr=0.001，γ=0.999，step_size=10。

3.3 实验结果与分析

本节在基准数据集上就相关评价指标对所建模型及基线模型的相关实验结果进行分析讨论，并验证主要参数设置与模型设计的合理性。文中述及的预测结果均指测试集上的相关结果，验证结果均指验证集上的相关结果。

3.3.1 模型预测精度

基于所建模型IncDEST-GCN，实验在基准数据集PEMSD7-S 上预测未来15，30 和45 min 的交通流量，在数据集PEMS-BAY 上预测未来15，30和60 min的交通流量，其具体结果如表1所示。为方便比较，表1 列出所建模型IncDEST-GCN 以及8个基线模型[14]在2个基准数据集上的预测结果。

表 1 PEMSD7-S和PEMS-BAY数据集上不同模型的交通流预测精度Table 1 Traffic flow prediction accuracy of different models on PEMSD7-S and PEMS-BAY

由表1 中结果可见，本文所建模型IncDESTGCN 相较传统模型HA 与ARIMA 等，在3 个评价指标上均有大幅提升，并几乎优于包括近期提出的基于各种神经网络的所有基线模型(总共18 个结果中最优结果14 个)，特别是在长步长的预测上表现最优。例如PEMSD7-S 数据集上未来45 min 的预测以及PEMS-BAY 数据集上未来60 min的预测，3 个评价指标均有提升。注意到所建模型采用单“三明治”式的轻量结构，表明其结构简洁而有效，能深度捕获交通预测中的时空特性，并在一定程度上提升预测精度。新近模型SLCNN 的预测效果与本文所建模型相对接近，但采用了更为复杂的结构学习模型，其训练代价数十倍于本文模型(见下文)。

3.3.2 模型训练时间

此处讨论所建模型的训练时间代价。具体，在PEMSD7-S与PEMS-BAY 2个基准数据集上分别运行基线模型STGCN 与DCRNN。对于SLCNN 模型，由于其作者未开源其代码，本文采信文献[14]所报告的训练时间，根据其相较STGCN 与DCRNN的相对倍数给出结果。

图4 展示了包括本文所建模型在内的4 个模型单个Epoch所费的平均时间代价。具体，以所建模型IncDEST-GCN 所费训练时间为1 个时间单位，其他模型则根据其所费时间相较IncDEST-GCN 训练时间的倍数得到。由图4可见，所建模型相较基线模型中预测效果最好的SLCNN，其训练速度提升了30 倍以上；较之训练时间相对较短的STGCN，其训练时间则不到前者的2/3，而其预测精度则有明显提升。2 个基准数据集上所建模型的相对训练时间代价几乎完全一致。结果表明，所建模型的轻量化结构能有效平衡模型的预测精度与训练代价。

3.3.3 多层GCN

此处引入多层GCN，讨论其在交通流预测精度上的价值及其可能导致的过平滑。具体，时空卷积模块中分别采用1～4 层GCN，不使用丢边策略(模型简记为WODEST-GCN)，其结果如图5 所示。图5(a)，5(b)和5(c)3 个子图分别对应3 个评价指标；子图中的4 条曲线分别表示不同GCN 层数的模型。由图5 可见，当层数≤3 时，随GCN 层数加深，3个评价指标均有所下降，但加深到4层时，3 个指标均出现较大幅度的反弹，预测精度在MAE 和RMSE 2 个指标有所上升。由此可见，GCN 层数太少难以充分提取路网拓扑结构的空间特征，但单纯增加GCN层数带来的性能提升有限，甚至导致节点上的特征信息趋同而产生过平滑。因此，需要引入某种有效策略基于多层GCN 捕获高阶邻居节点信息的同时消解其可能导致的过平滑。

3.3.4 递增式丢边

针对过平滑问题，提出递增式丢边策略。为方便比较，此处也引入恒定比率丢边策略(简记为FixDEST-GCN)，相应结果如图6 所示。由图6 可见，相较不使用丢边与恒定比率丢边，递增式丢边策略在3个预测指标上具有稳健优势；恒定比率丢边策略相较不使用丢边策略，预测精度也有明显提升，但弱于递增式丢边。由此可见，本文所拟丢边策略能在一定程度上抑制过平滑，进而有效利用高阶邻居节点相关信息。进一步，实验递增式丢边策略在不同GCN层数情形下的预测表现，其结果如图7 所示。图7 中没有出现预测性能的明显反弹，递增式丢边模型的预测精度随GCN 层数增加而稳步提升，再次验证所拟策略的有效性。

3.3.5 交通流速节点离散性

如前文所述，简单增加GCN 层数可能导致节点特征趋同而出现过平滑。不难理解，节点特征趋同会导致网络结构类似节点上的预测趋同，其预测值的离散性会有所降低。为此，实验观察路网节点上的预测精度与离散性，结果如图8 与表2所示。

图8 绘制了PEMSD7-S 预测集中随机抽取的4个样本时间帧上各节点的真实交通流速以及使用递增式丢边与不使用丢边2种模型下预测的交通流速的箱线图以观察其分布特征。由图8可见，相较2 个预测模型，真实交通流速影响因素多(甚或带有一定噪声)而分布离散程度最大。不丢边模型的预测值离散程度最小，表明其预测值在各节点上相对更为接近，有一定程度的过平滑而欠拟合。本文所建模型则取得了更优的平衡，其离散程度介于前述两者之间，一定程度上消解了过平滑。

表 2 PEMSD7-S数据集上不同模型的预测误差分位数表Table 2 Quantiles prediction error of different models on PEMSD7-S

表2 以分位数方式展现2 种模型预测误差的分布情况。由表2清晰可见，对应分位点上，使用递增式丢边策略的模型IncDEST-GCN 的预测误差更低，不使用丢边策略的模型WODEST-GCN 的预测误差则更为离散，再次验证本文所建模型与所拟相关策略的有效性。

3.3.6 参数设置与深层模型实验

前文递增式丢边比例等参数设置实为适当调试后的选择，此处验证其合理性。可行参数组合数量巨大，表3 仅取典型组合以清晰展示。其中0.1～0.4表示4层GCN中丢边比例依次为0.1，0.2，0.3 和0.4，其他依此类推。由表3 结果可见，比例为0.2，0.3，0.4 和0.5 的丢边设置在多种情形下整体表现最佳。实际应用中可根据预测时长等具体情形调适。在数据集PEMS-BAY 上也可观察到类似情形，此处不再赘述。

表 3 PEMSD7-S数据集上不同递增式丢边参数的验证结果Table 3 Validation performance of IncDEST-GCN with different DropEdge rations on PEMSD7-S

进一步，实验增加GCN 层数以观察更深层数GCN 的边际效能。图9 展示了PEMSD7-S 数据集上45 min的预测结果(深层GCN 在更短时长上的预测表现不佳)。由图9 可见，以更高的模型复杂度与计算代价，更深的GCN 在长时预测精度上有一定边际改善。其中5 层GCN 在RMSE 指标上表现最好，6层GCN 在其他2个指标上表现最好。相较之下，4层GCN 以适度的计算代价在3个指标上均表现稳健，这也是本文以4 层GCN 为基础结构的原因。

4 结论

1) 针对路网交通流预测所具有的天然时空依赖性，基于时空图卷积神经网络构建预测模型，实现交通流时空特征的有效融合；针对时空图卷积时空交互所涉计算量大而耗时长等问题，构建“厚夹心”单“三明治”式时空卷积模块，轻量化模型结构的同时能提升其预测性能；针对多层空间卷积潜在的过平滑风险，引入递增式丢边策略，有效捕获高阶邻居节点信息，避免节点交通流信息特征失效。

2) 所建模型相较基线模型中预测精度最高的SLCNN 模型，压缩训练时间30 倍以上；相较基于图神经网络的类似模型STGCN，则能以不到2/3的训练时间取得明显预测精度提升。

基于时空图神经网络处理交通流信息方兴未艾，后期研究将尝试新型时空信息融合模块，结合注意力策略，构建基于动态图的交通流模型等。