考虑线上电子优惠券投放的BOPS渠道整合
王雪茹
(重庆交通大学经济与管理学院,重庆 400074)
0 引言
随着互联网的发展,网购渐渐成为大家生活中的必备。但是网购存在消费者无法现实体验物品的问题所以容易产生退货的情况,所以顺势出现了以“线上购买,线下取货”(BOPS)为主的“全渠道零售”,该模式通过线上线下渠道的整合,让消费者体会到完美的购物体验。有些零售企业为了刺激消费,又采取了在线上投放电子优惠券的营销模式,探讨制造商在不同情况时分别如何制定均衡价格、优惠券面值是全渠道整合中非常重要的部分。
以往文献中关于全渠道的研究多在于从消费者角度等。例如Gallio和Moreno[1]通过实证研究分析了BOPS模式对供应链及成员的影响。Gao和Su[3]研究BOPS策略对不同类型产品和消费者的影响。罗美玲[4]考虑在多渠道供应链中,产品匹配率影响消费者退货的情况下,对基于电子优惠券的整合策略进行了研究。王聪和杨德礼[5]发现合理金额的折扣券可增进电商平台与双渠道制造商的合作。
1 问题描述与模型假设
考虑一个主导制造商,它分线上直销和线下两种渠道销售产品。在此基础上,增加一种线上购物线下自提的渠道,制造商与零售商线下实体店达成合作,制造商给零售商单位产品佣金补偿。此外,制造商在BOPS渠道投放电子优惠券刺激消费。基于该供应链结构构建制造商和零售商组成的stackelberg博弈模型,并假设该制造商是零售商的唯一制造商,且在供应链中占主导地位,接着,分别用公式表示三种渠道消费者的需求。
1)仅去线上的消费者,需求可以表示为:De=βa-p。
2)BOPS类消费者:Dp=γa+m-p+μf(0<μ<1)。
3)仅去线下传统零售渠道购买的消费者:Dt=(1-β-γ)a+m-p。
本文研究过程中涉及的参数及其含义总结如表1所示。

表1 参数及意义
2 模型构建与分析
2.1 线上下同价
首先考虑线上下同价的BOPS供应链集中决策模型,整体供应链利润函数为:
πt=(p-f)Dp+P(De+Dt)=(p-f)(γa-p+μf+m)+p[(1-γ)a+m-2p]
(1)
由此式可知整个BOPS全渠道供应链的利润函数是关于价格和优惠券的二元凹函数,因此对其分别求关于(p,f)的一阶偏导并令其等于零,可得命题1。
命题1:当BOPS线上下同价,供应链集中决策且在BOPS渠道投放线上优惠券时,最优线上下价格和优惠券面额为:
此时供应链整体利润为:
π*t=
证明:由于集中式情境下价格p和优惠券面值f同时决策,对两变量求一阶偏导,利润函数对价格P和优惠券f求二阶导得相应的Hesse矩阵如下:
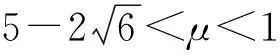
推论1:线上下同价且集中决策下均衡价格、均衡优惠券面值以及最大利润与β即线上消费者比例无关。
(2)
BOPS渠道的消费者比例越多,线上下的均衡价格以及优惠券越低。消费者越偏好于BOPS渠道,就要在其他渠道多吸引消费者。
在设计道路横断面的过程中,首先需要确保整体城市道路系统具有良好的协调性,在城市规划红线范围内,通过充分结合实际通行情况以及周边建筑等其他相关资料进行道路横断面设计,使其能够在与周围建筑、城市小品等相互协调的基础上确保行人以及车辆的通行安全[1]。其次,在设计过程中需要严格依照道路自身的功能、性质等,在确定城市道路具体等级如主次干道、快速路等基础上,参考城市绿化覆盖率,依照国家规定的设计规程合理布设城市道路横断面,使其能够与道路等级要求相符合。另外,设计人员还需要在设计时充分考虑道路排水以及各地下管线的实际情况,以防止出现后期道路横断面施工影响正常道路排水或破坏地下管线的情况。
2.2 线上下不同价
分散决策中,制造商和零售商独自决策,此时制造商和零售商各自的利润为:
πm=peD′e+(pe-f-h)D′p+wD′t
=pe(βa-pe)+(pe-f-h)(γa+m-pe+μf)+w[(1-β-γ)a+m-pt]
πr=(pt-w)D′t+hD′p=(pt-w)[(1-β-γ)a+m-pt]+h(γa+m-pe+μf)
根据逆向归纳法,首先决策零售商线下价格。给定制造商的决策w和f,零售商确定pt,最大化自己的利润。
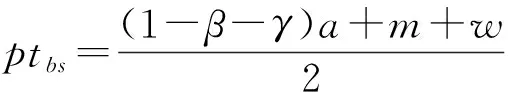
将其带入制造商利润函数并分别对(pe,w,f)求一阶偏导并令其为零,得到命题2。
命题2:分散决策时,均衡线上价格、优惠券面值以及成本为:
证明同上。推论2:
消费者越偏好于BOPS渠道,零售商得到制造商的补偿越多,通过BOPS渠道获得的单位收益越小,不愿面对BOPS渠道可能存在低收益的情况。零售商则为了与制造商竞争降低自己的价格。
3 数值分析
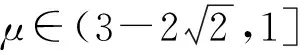
3.1 μ和m对定价和优惠券面值的影响
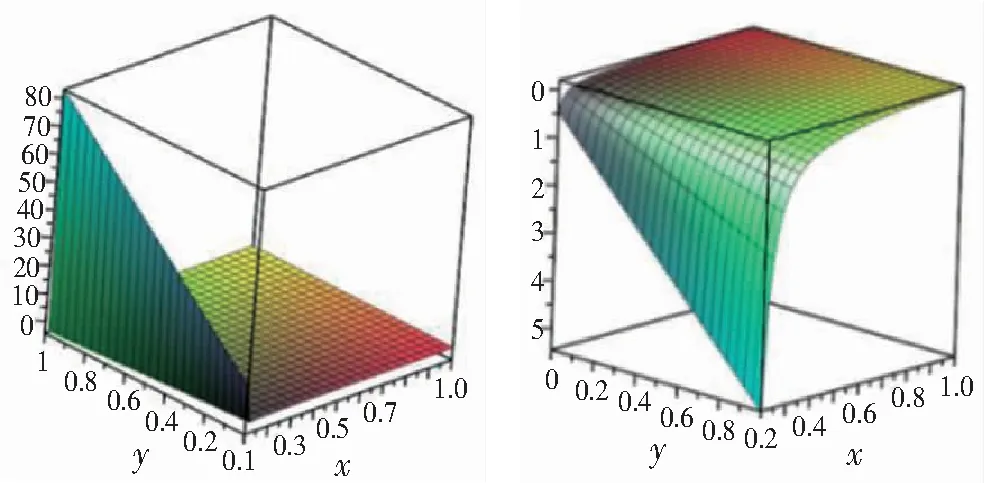
图1 均衡价格受μ、m的影响
2)两种情况下制造商制定的优惠券面值f随μ和m的影响如图2所示。
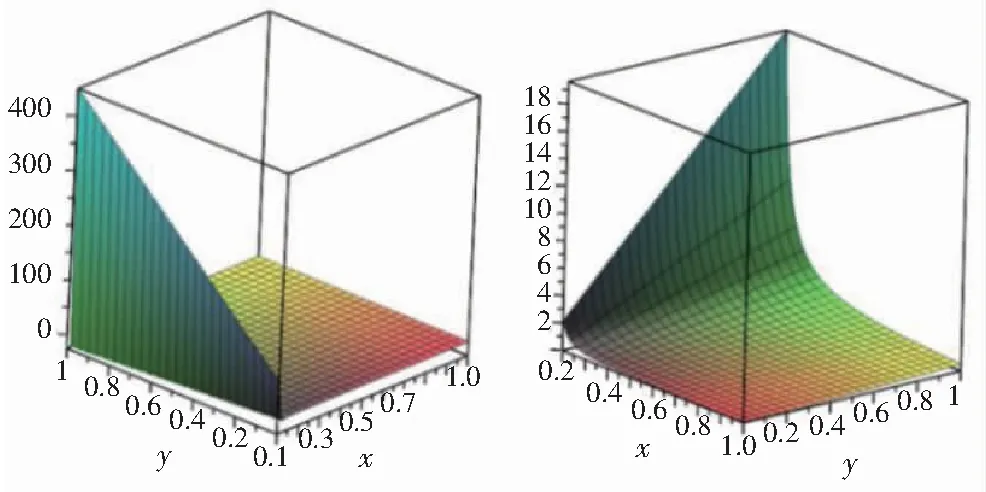
图2 优惠券面值随μ和m的影响
从图1~2中可以看出,线上下同价时,均衡价格与μ的值无关,与m正相关。优惠券面值与μ的值无关,与m负相关。
线上下不同价时,线上均衡价格和μ的值负相关,与m正相关。优惠券面值和μ的值负相关,因为μ越大对优惠券的需求越大,制造商边际收益减小,所以制定的线上均衡的价格以及优惠券面值要相应降低。与m负相关。
3.2 μ和m对制造商、零售商和总利润的影响
线上下同价时总利润以及线上下不同价时零售商利润、制造商利润如图3所示。
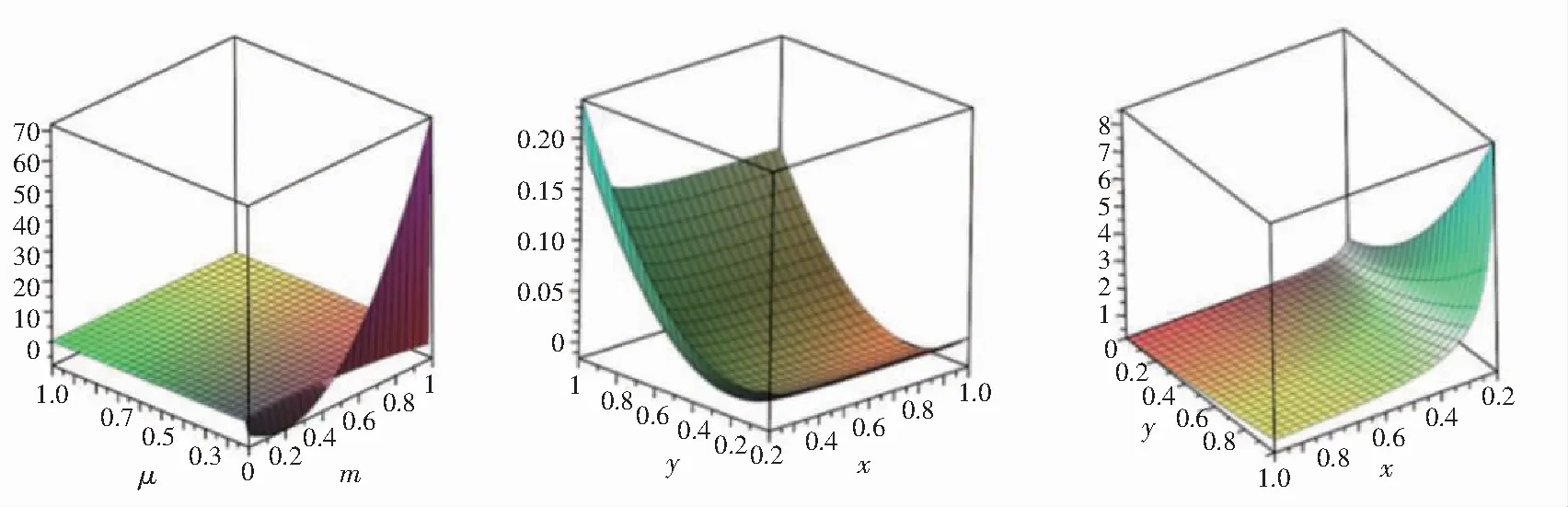
图3 总利润 零售商利润πr 制造商利润πm
1)线上下同价时总利润与μ无关,随m的增加先减少后增加。
2)线上下不同价时零售商利润随μ的增加先降低又升高,随m的增加先降低又升高。当μ比较小时,优惠券需求弹性较小。μ增大以后,消费者对优惠券的敏感度升高,零售商可获得制造商的优惠券促销利好,其利润亦增加。
制造商利润刚开始与μ无关后来与μ正相关,与m成正相关。
刚开始投放优惠券时消费者对优惠券的敏感性较低,所以制造商利润不变。当μ越来越大时,消费者对优惠券的敏感度增加,制造商整体收益升高。当m逐渐增大时,消费者会更多投入到线下以及BOPS渠道,所以制造商可凭此制定高价获取更多利润。
4 结论与启示
1)线上下同价集中决策中,制造商制定的均衡价格和优惠券面值随BOPS渠道消费者比例增大而降低,同时均衡价格随线下服务带来需求的增加而增加,优惠券面值随线下服务带来需求的增加而降低。
2)线上下同价时,优惠券需求弹性系数的值不影响均衡价格、优惠券以及整体利润,而线上下不同价时均衡价格和优惠券都与其负相关,而分散决策时零售商利润和制造商利润最终都是与优惠券需求弹性系数和线下服务需求系数成正比。说明企业如果实行上下线同价的策略时优惠券对企业整体无太大关系,投放优惠券是无意义的。而上下不同价分散决策时优惠券以及线下的服务都能给整体利润带来增长,不过投放后要等一定的时日才能有明显的利润增长。
3)针对不同的优惠券需求以及线下服务需求,要制定相应的定价方法,集中决策时的线上均衡价格以及优惠券面值要相应的比分散决策小,企业要针对具体商品情况选择决策方式。
对于全渠道零售中优惠券以及线下服务对消费者需求的影响以及对供应链整体利润的影响得出的结论,可以用于企业管理中。但是对于具体线下服务成本的涉及不够细致,没有考虑消费者类型,可以在以后的研究中继续深入。

