Two-Higgs-doublet models in light of current experiments: a brief review
Lei Wang,Jin Min Yang and Yang Zhang
1 Department of Physics,Yantai University,Yantai 264005,China
2 CAS Key Laboratory of Theoretical Physics,Institute of Theoretical Physics,Chinese Academy of Sciences,Beijing 100190,China
3 School of Physical Science,University of Chinese Academy of Sciences,Beijing 100049,China
4 School of Physics and Microelectronics,Zhengzhou University,ZhengZhou 450001,China
Abstract We briefly survey several typical CP-conserving two-Higgs-doublet models(2HDMs)in light of current experiments.First we derive the masses and couplings of the mass eigenstates from the Lagrangians.Then we analyze the constraints from theory and oblique electroweak parameters.Finally,we delineate the status of 2HDM in light of the LHC searches,the dark matter detections and the muon g-2 measurement.
Keywords: two-Higgs-doublet model,LHC,dark matter,muon anomalous magnetic moment
1.Introduction
A two-Higgs-doublet model(2HDM)is a simple extension of the Standard Model(SM)by introducing an additional SU(2)LHiggs doublet,which predicts three neutral Higgs bosons and a pair of charged Higgs bosons H±.The 2HDM can be CPviolating [1],but it is also useful to study its CP conserving version,where the neutral Higgs bosons can be classified into the CP-even states (h and H) and the CP-odd state (A).The tree-level flavour changing neutral current(FCNC)can appear in the general 2HDM,which is forbidden by imposing Z2discrete symmetry in several different ways,such as type-I 2HDM [2,3],type-II 2HDM [2,4],lepton-specific 2HDM(L2HDM),flipped 2HDM [5–10],and inert 2HDM [11–13].Also the tree-level FCNC is absent in the aligned 2HDM in which the Yukawa-coupling matrices of the two Higgs doublet fields are assumed to be proportional [14].In addition,due to a certain type of symmetry,the FCNC is naturally suppressed by the off-diagonal element of the CKM matrix in the Branco–Grimus–Lavoura 2HDM [15].
Various 2HDMs have been extensively studied in particle physics.Because of the plentiful Yukawa couplings of the quarks and leptons,the 2HDMs have been studied in meson decays,and the L2HDM is used to explain the muon g-2 anomaly [22,16–20,171,23–33].In the inert 2HDM,one may take the lightest component of the inert Higgs doublet field is neutral,and consider it as a dark matter (DM) candidate because of its stability.If an additional field protected by a new symmetry is added to other types of 2HDMs,then these models also can provide a DM candidate.In these models,the multiple scalar fields can be the portals between the DM and the SM sector,and lead to some interesting effects on the DM observables via their various Yukawa couplings[34–50].On the other hand,the analyses of ATLAS and CMS collaborations at the LHC show that the properties of the discovered 125 GeV Higgs boson agree well with the SM Higgs boson [51,52].Other than that,no experiment claims to have observed any new resonance with 5σ level.However,there are some interesting excesses that imply the existence of new scalars.For example,the CMS Run II results for Higgs boson searches in the diphoton final state show a local excess of~3σ around 96 GeV [53].The ATLAS collaboration reported a local excess of~3σ around 130 GeV in the searches for t→H±b with H±→cb [54].Besides,very recently the CDF II result for the W-mass has an approximate 7σ discrepancy from the SM prediction [55].The 2HDM can give additional corrections to the masses of gauge bosons via the self-energy diagrams exchanging extra Higgs fields,and simply explain the CDF W-mass when the extra Higgses have appropriate mass splittings (see e.g.[56–69]).
In the literature there already have been some reviews on 2HDMs(see e.g.[70–75]).In this note we emphasize current experiments and briefly review several typical CP-conserving 2HDMs.We will start from the Lagrangians and derive the masses and couplings of the particles.Then we analyze the constraints from theory and oblique electroweak parameters,respectively.Finally,we discuss the status of 2HDMs in light of the LHC searches,the dark matter detections and the muon g-2 measurement.
The content is organized as follows.In sections 2 and 3,we demonstrate several typical CP-conserving 2HDMs and discuss the constraints from theory and oblique parameters.In sections 4,5,and 6,we review the status of the 2HDMs in light of the LHC Higgs searches,the DM detections and the muon g-2 measurement.Finally,we give a summary in section 7.
2.Several typical 2HDMs
The general scalar potential of 2HDM is given as

and the Φ1and Φ2are complex Higgs doublets with hypercharge Y=1:

Here we restrict to the CP-conserving models in which all λiandm122are real and the electroweak vacuum expectation values (VEVs) v1and v2are also real withv2=v12+v22=(2 46 GeV)2.
2.1.Type-I,type-II,lepton-specific and flipped 2HDMs
In order to forbid tree-level FCNC,one may introduce an additional Z2discrete symmetry under which the charge assignments of fields are shown in table 1.Because of this Z2symmetry,the λ6and λ7terms in the general scalar potential in equation (2.1) are absent,while the soft breakingm122term is still allowed.The mass parametersm112andm222in the potential are determined by the potential minimization conditions at (v1,v2):

where the shorthand notationscβ≡cosβ,and λ345=λ3+λ4+λ5are employed.
From the scalar potential in equation (2.1) with λ6=λ7=0,we can obtain the mass matrices of the Higgs fields

The mass eigenstates are obtained from the original fields by the rotation matrices:

where G0and G±are Goldstone bosons which are absorbed as longitudinal components of the Z and W±bosons.The remained physical states are two neutral CP-even states h and H,one neutral pseudoscalar A,and a pair of charged scalars H±.Their masses are given by


whereMP2is the mass matrix shown in equation (2.4).
The gauge-kinetic Lagrangian is given as

We can obtain the neutral Higgs couplings to VV (VV ≡ZZ,WW)
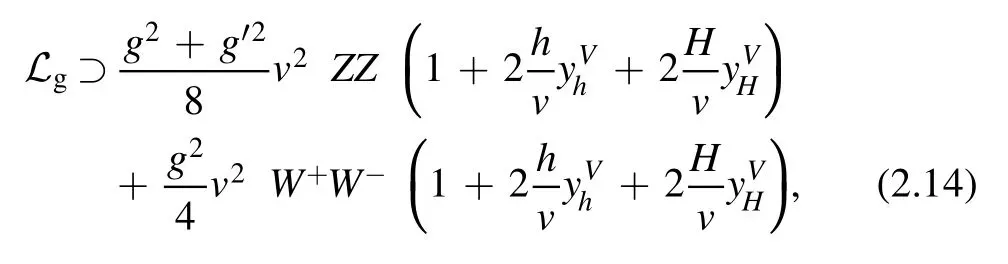
whereyhV=sin(β-α)andyHV=cos(β-α).
According to different charge assignments,there are four different models with Yukawa interactions:

whereQLT=(uL,dL),LLT=(νL,lL),=iτ2Φ*1,2,and Yu2,Yd1,2and Yℓ1,2are 3×3 matrices in family space.
We can obtain the Yukawa couplings

whereyhf=sin(β-α)+cos (β-α)кfandyHf=cos(β-α)-sin (β-α)кf.The values of кu,кdand кℓfor the four models are shown in table 2.
2.2.Inert Higgs doublet model
We impose an exact Z2discrete symmetry in the 2HDM and assume that it remains after the potential minimization.Under the Z2symmetry all the SM fields are taken to be even,while the new (inert) doublet Φ2is odd:

The Φ1field has a vev v=246 GeV,and Φ2has no vev.
The scalar potential is

The parameterm112is fixed by the scalar potential minimum conditions

The fields H±and A are the mass eigenstates and their masses are given by

There is no mixing between h and H,which are the CP-even mass eigenstates

The fermion masses can be obtained via the Yukawa interactions with Φ1

where yu,ydand yℓare 3×3 matrices in family space.Because of the exact Z2symmetry,the inert field Φ2has no Yukawa interactions with fermions.The lightest neutral field,H or A,is stable and may be considered a DM candidate.If right-handed neutrinos are introduced,then Φ2can interact with them,giving rise to the neutrino masses via the one loop with DM [76].
3.Constraints from theory and oblique parameters
3.1.Vacuum stability
Vacuum stability requires the potential to be bounded from below and stay positive for arbitrarily large values of the fields.The Higgs potential with a soft Z2symmetry breaking term is given by
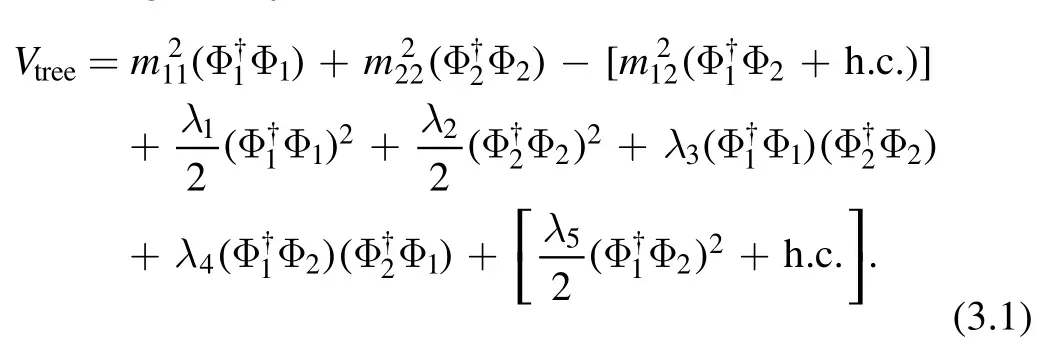
The fields can be parametrized as

For large values of the fields,the quadratic terms can be neglected and the quartic part is

After stabilizing θ at the minimum,we obtain the θ-independent part of potential
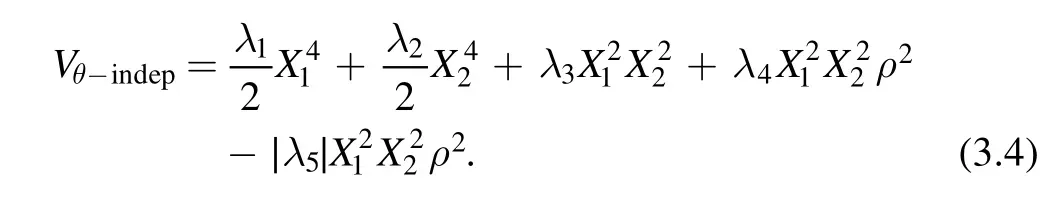
For λ4-|λ5|>0,the potential has a minimal value at ρ=0,

For λ4-|λ5|<0,the potential has a minimal value at ρ=1,

Therefore,the vacuum stability requires

In addition,there is the possibility that the 2HDM scalar potential of equation (3.1) has two minima,and the selected minimum is required to be global in order to avoid a metastable vacuum,which imposes the following condition [77],

3.2.Unitarity
The amplitudes for scalar–scalar scattering s1s2→s3s4at high energies respect unitarity [78].A simple and explicit derivation can also be found in [79].The starting point is the unitarity of the S matrix,S=1+iT,

Then in terms of matrix elements of scattering from a pair of particles a=1,2 with momenta p1,p2to a pair b=3,4 with momenta k3,k4we have

We can obtain a bound on the partial wave
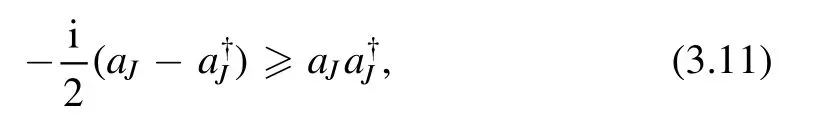
where aJis a normal matrix related to the partial wave decomposition of 2→2 scattering matrix elements Mba,

The factor δ12(δ34) is 1 when the particles 1 and 2 (3 and 4)are identical,and zero otherwise.PJare the Legendre polynomials,piis the centre-of-mass three-momentum for particle i,ands=(p1+p2)2is the standard Mandelstam variable.
We can diagonalize a and a†in equation (3.11) with a unitary matrix,and obtain the constraints on the eigenvalues(aJi):
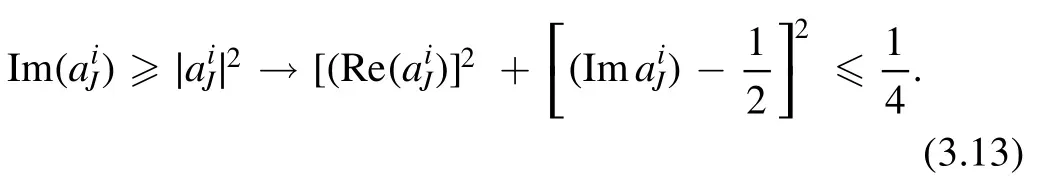
At tree-level,the bound is generally relaxed to

We assume the external masses of s1,2,3,4are vanishing at a high energy limit,and focus on the J=0 partial wave.The modified zeroth partial wave for s1s2→s3s4is

where Q1234is a quartic coupling of s1s2s3s4.
Now we study the unitarity constraints on the 2HDM scalar potential.For the scalar potential in equation(3.1),one can take the uncoupled sets of scalar pairs

to construct the matrix containing the tree-level amplitudes for s1s2→s3s4.We can obtain different eigenvalues of these matrices [80,81]


The unitarity of the scattering processs1s2→s3s4leads to

Here we stress that the conditions of equation (3.27) just indicate the approximate level above which the tree-level scattering amplitudes do not provide reliable results anymore.The problem is that we cannot rely on perturbative expansion when analyzing scattering,and therefore equation (3.27) is just our safety check,not the strict theory limitation.In addition,we take the standard approach to derive equations (3.15) and (3.27) and only consider quartic pointlike couplings in the high energy limit.At finite energy,the additional diagrams of s,t,u channel in s1s2→s3s4scattering can give some corrections to equations(3.15)and(3.27)[82].
3.3.Oblique parameters
The 2HDM can give additional contributions to gauge boson self-energies by the exchange of extra Higgs fields in the loops.The oblique parameters S,T and U were used to describe deviations of 2HDM from the SM,which are given as [83–85]

where
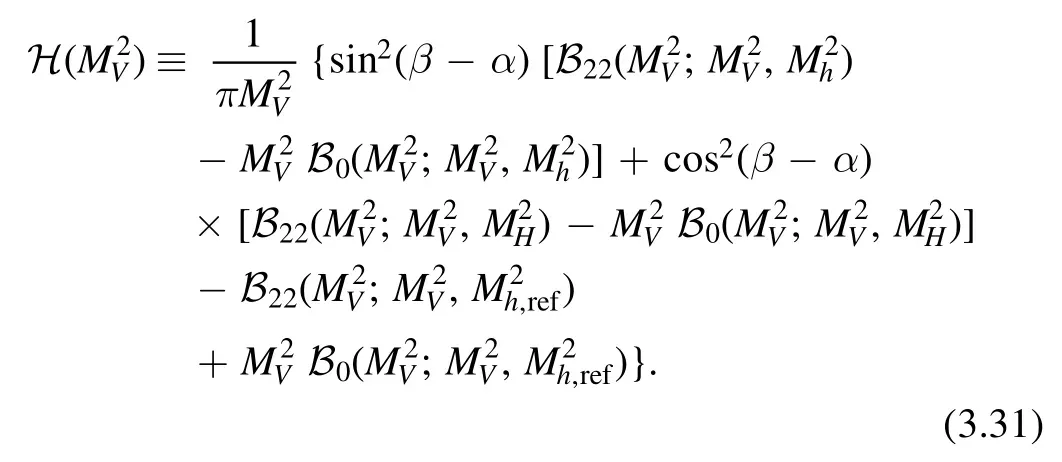
The loop functions are given by

where
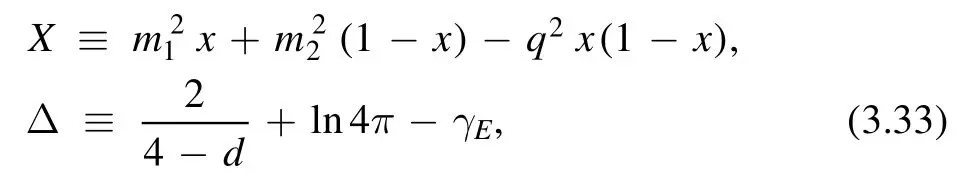
in d space-time dimensions.TheB22andB0functions are defined as

The above expressions show that the oblique parameters S,T and U are sensitive to the mass splitting of extra Higgs bosons.If h is taken as the 125 GeV Higgs,H or A is favored to have small mass splitting from H±.Figure 1 shows mHand mAfor type-II 2HDM allowed by the global fit values to the oblique parameters [86]

with correlation coefficients

In figure 1mH±>570 GeV is taken to satisfy the constraints of the experimental data of b→sγ [88].
Very recently the CDF collaboration reported their new result for the W-boson mass measurement [55]

which has an approximate 7σ deviation from the SM prediction,mW(SM)=80.357±0.006 GeV [89].The shifted
W-mass modifies the global fit values to S,T,and U [90]

Figure 1.Scatter plots of mA and mH satisfying the constraints of vacuum stability,unitarity,perturbativity,and the oblique parameters for 570 GeV≤ mH±≤900 GeV,taken from [87].
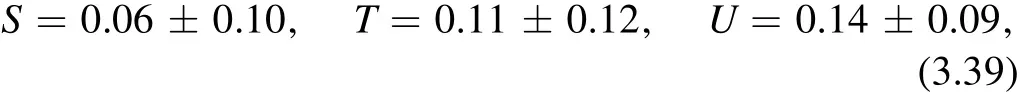
with correlation coefficients

The W-boson mass can be inferred from the following relation[91],

In the 2HDM,the correction to T is usually larger than S and U.In order to accommodate the W-mass reported by the CDF II collaboration,the 2HDM needs to give an appropriate value of T.Therefore,H/A is disfavored to degenerate in mass with H±.Various types of 2HDMs have been used to explain the W-mass [56–69].Reference [59]discussed the CDF W-mass in the 2HDM with an exact Z4symmetry and found that the CDF W-mass favors the mass splitting between H±and H/A to be larger than 10 GeV,and allows H and A to degenerate.The±mHand mAare favored to be smaller than 650 GeV for mH<120 GeV,and allowed to have more large values with increasing of mH.
4.Constraints from LHC searches for Higgs bosons
4.1.Signal data of the 125 GeV Higgs
In the four types of 2HDMs,the neutral Higgs Yukawa couplings normalized to the SM are given by


The neutral Higgs couplings with gauge bosons normalized to the SM are

with V denoting W or Z.
The analyses of ATLAS and CMS collaborations show that the coupling strengths of the discovered 125 GeV boson agree well with the SM Higgs boson,but the sign of the couplings cannot be measured directly.If we take h as the 125 GeV Higgs boson,its couplings have two different cases:

In the case of the SM-like couplings,the couplings of the 125 GeV Higgs are very close to those in the SM,which has an alignment limit.In the exact alignment limit [92,93],namely cos (β-α)=0,from equations (4.1) and (4.5) we see that h has the same couplings to the fermions and gauge bosons as in the SM,and the heavy CP-even Higgs H has no couplings to the gauge bosons.
Now we discuss the wrong-sign Yukawa couplings [87,94–109].The signal data of the 125 GeV Higgs require the absolute values ofyhfiandyhVto be close to 1.0.Thus,we approximately expressyhfiandyhVwith ∈and (β-α)
cos as


Figure 2.Scatter plots of sin(β-α)andtan βof type-II model satisfying the constraints of the 125 GeV Higgs signal data,taken from[112].
From equation (4.1) we can get

In the four types of 2HDMs,the measurement of the branching fraction of b→sγ favors atanβgreater than 1.Therefore,for sin (β-α)>0 and cos(β-α)>0,there may exist wrong-sign Yukawa couplings for the down-type quarks and leptons in the type-II model,for the leptons in the L2HDM,and for the down-type quarks in the flipped 2HDM.
Figure 2 shows sin (β-α)andtanβof type-II model allowed by the 125 GeV Higgs signal data.The value of sin(β-α)in the case of the wrong-sign Yukawa couplings is allowed to deviate from 1 more sizably than in the case of the SM-like couplings.In the case of the wrong-sign Yukawa couplings,tanβhas stringent upper and lower bounds for a given value of sin (β-α).
4.2.Searches for additional scalars at LHC
The ATLAS and CMS collaborations have searched for an additional scalar from its decay into various SM channels or from its exotic decays.Since the Yukawa couplings of downtype quarks and leptons can be both enhanced by a factor of tanβ,the type-II model can be more stringently constrained than the other three types of models by the flavor observables and the LHC searches for additional Higgs.
At the LHC,the dominant production processes of H and A are from the gluon–gluon fusions,which are generated by exchanging top quark and b-quark in the loops.There may be destructive interference between contributions of b-quark loop and top quark loop.The SusHi [110]was used to cal--associated production atNNLO in QCD,whilethe culate the cross sections for H and A in the gluon fusion and 2HDMC was employed to precisely calculate the branching ratios of the various decay modes of H and A [111].
The studies in [87,112]used a large number of ATLAS and CMS analyses at the 8 TeV and 13 TeV LHC to constrain the type-II 2HDM.Table 3 lists some analyses at the 13 TeV LHC with more than 35.9 fb-1integrated luminosity data.Figure 3 shows the surviving samples with the SM-like coupling of the type-II model satisfying various LHC direct searches.The couplings of AhZ and AHZ are respectively proportional to cos(β-α)and sin (β-α).For the case of the SM-like coupling,∣sin (β-α)∣is very closed to 1.Therefore,the A→hZ channel fails to constrain the parameter space,and the A→HZ channel can exclude many points in the region of mH<360 GeV.The H/A→τ+τ-channels give an upper bound ontanβ,and allow mHto vary from 150 GeV to 800 GeV for appropriatetanβand sin (β-α).Figure 3 shows the joint constraints of H/A→τ+τ-,A→HZ,H→WW,ZZ,γγ,and H→hh exclude the whole region of mH<360 GeV.

Table 1.The Z2 charge assignment in the four types of 2HDMs without FCNC.The other fields are even under Z2 symmetry.

Table 2.The кu,кd,and кℓ for the four types of 2HDMs.
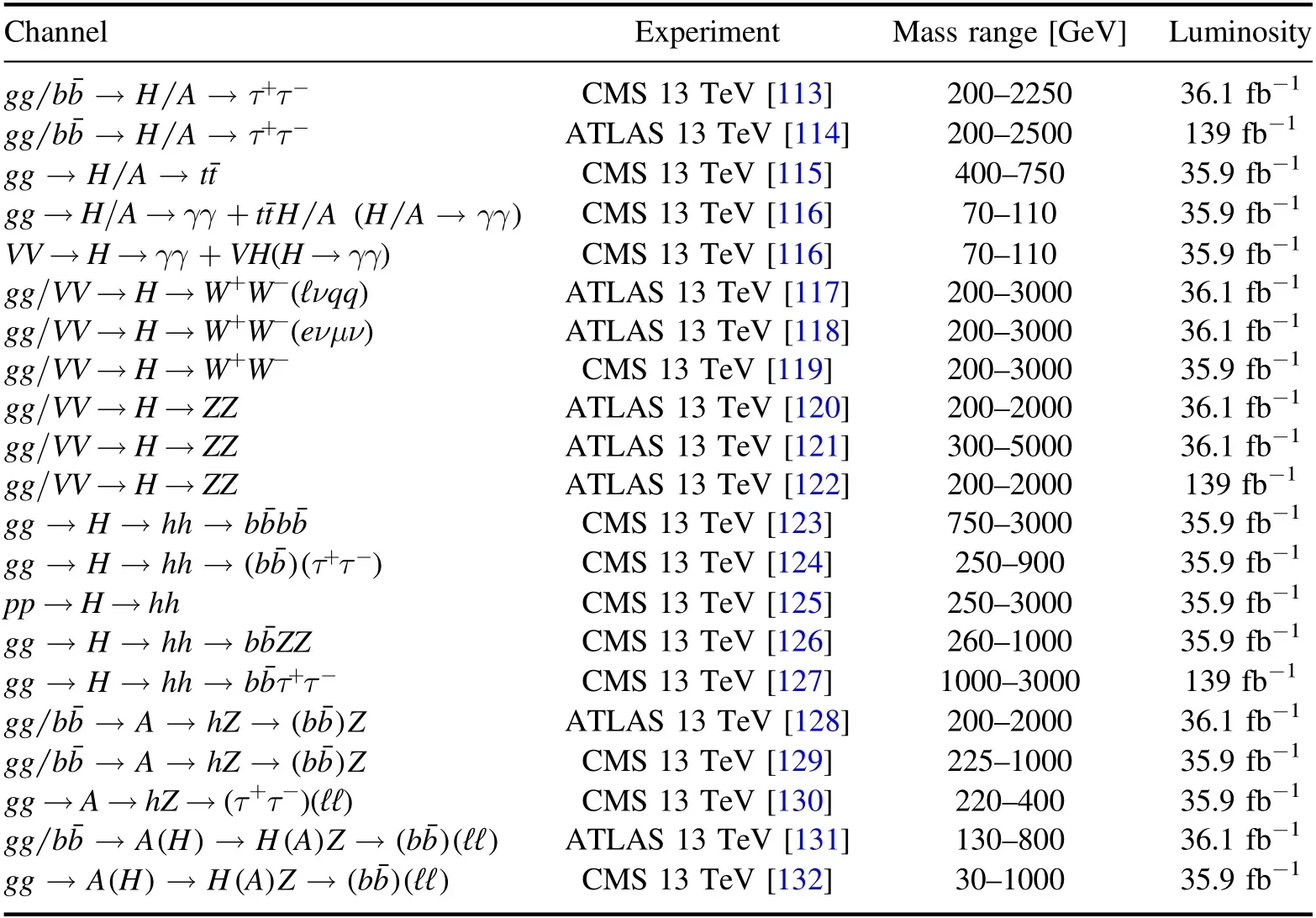
Table 3.The upper limits at 95%C.L.on the production cross section times branching ratio for the channels of H and A searches at the LHC.

Table 4.The Z4 charge assignment of μ–τ-philic 2HDM.

Figure 3.The surviving samples with the SM-like couplings of type-II model,taken from[112].The triangles(sky blue),circles(royal blue),squares (black),inverted triangles (purple),and pluses (red) are respectively excluded by the H/A→τ+τ-,H→WW,ZZ,γγ,H→hh,A→HZ,and A→hZ channels at the LHC.The bullets (green) samples are allowed by various LHC direct searches.

Figure 4.The surviving samples with the wrong-sign Yukawa couplings of the type-II model,taken from[87].The triangles(sky blue)and pluses(red)are respectively excluded by the A/H→τ+τ-and A→hZ channels at the LHC.The bullets(green)are allowed by various LHC direct searches.

Figure 5.Left:fn/fp versus yd/yu with yd(yu)denoting the Yukawa coupling of(hu)normalized to the SM value[42].Right:All the samples are allowed by the constraints of the LHC searches and the DM relic density.The pluses(red)are excluded by the constraints of the spin-independent DM-proton cross section from XENON1T(2017),and the triangles(royal blue)are excluded by the Fermi-LAT search for DM annihilation from dSphs [42].
The surviving samples with the wrong-sign Yukawa couplings of the type-II model are shown in figure 4.For the case of the wrong-sign Yukawa couplings,the signal data of the 125 GeV Higgs requirestanβ>5 and allows sin(β-α)to be as low as 0.94,as shown in figure 2.As a result,the cross sections of H and A in the gluon fusion productions are sizably suppressed,and only→A→τ+τ-and A→hZ channels can be used to constrain the parameter space.Especially for mH=600 GeV,the constraints are very stringent,and the allowed samples are mainly distributed in several corners.Many samples with mAin the ranges of 30–120 GeV,240–300 GeV,380–430 GeV,and 480–550 GeV are allowed for appropriatetanβand sin (β-α).Also the samples in the regions of mA<20 GeV and 80 GeV<mA<90 GeV are allowed since there is no experimental data of A→τ+τ-channel in these ranges.
For the case of mA=600 GeV,the constraints of the→A→τ+τ-and A→hZ channels can be relatively relaxed.Many samples of 150 GeV<mH<470 GeV are allowed and mH>470 GeV is excluded.For a small mH,the A→HZ decay will open and increase the total width of A.As a result,the branching ratio of A→hZ can be sizably suppressed,and weaken the constraints of the A→hZ channel.
Compared to the type-II 2HDM,all the Yukawa couplings of H,A and H±in the type-I model can be suppressed by a largetanβ,which leads that the searches for additional scalars at the LHC and measurements of the flavor observables are easily satisfied.Thus,H,A and H±are allowed to have broad mass ranges.There are some recent studies on the status of type-I and type-II 2HDMs confronted with the direct searches at the LHC,see,e.g.[133–143].
5.Dark matter observables
5.1.Inert 2HDM and dark matter
Because of the exact Z2symmetry,the lightest neutral component H or A is stable and may be considered as a DM candidate.If taking H as the DM,it requires

Flipping the sign of λ5,A will be the DM candidate.The parameter λ345=λ3+λ4+λ5controls the hHH coupling,which will affect the signal strengths of the 125 GeV Higgs and the DM observables.
The main possible annihilation channels includeHH→,VV(*),hhand various co-annihilations of the inert scalars.In addition to the constraints from theory and the oblique parameters as well as the signal data of the 125 GeV Higgs,the model should also satisfy the precise measurements of the W and Z widths,which requires

The null searches at the LEP exclude two regions[144,145],
Considering various relevant theoretical and experimental constraints,the allowed DM mass ranges have been discussed,see e.g.[146–157].Because of the tension between the signal strength of the 125 GeV Higgs and the relic density,mH<55 GeV is disfavored.In the resonance region ofmH⋍,the main annihilation channels are h-mediated,primarily intoand WW final states.The correct relic density can be obtained and the relevant constraints can be satisfied.In the region up to around 75 GeV,the HH pair mainly annihilates to WW*via the processes mediated by h or via the quartic couplings.Under the relevant constraints,the correct relic density can be rendered for 73 GeV<mH<75 GeV.For 75 GeV<mH<160 GeV,the correct relic density requires λ345to be large enough to lead to an appropriate cancelation between diagrams of VV*.However,such a large λ345is excluded by the DM direct detections.In the region between 160 GeV and 500 GeV,the annihilation cross section of HH→W+W-is too large to produce the exact relic density.In the region of mH>500 GeV,the exact relic density favors small mass splittings among the three inert Higgs bosons,roughly≤10 GeV.The large mass splittings tend to enhance the cross section of HH annihilation into longitudinal Z and W bosons.
5.2.Wrong-sign Yukawa couplings and isospin-violating interactions between dark matter and nucleons.
Although the inert 2HDM may provide a DM candidate,its mass range is stringently constrained.Alternatively,a real singlet scalar DM can be added to the 2HDM,and this DM has different properties from the DM in inert 2HDM.Especially for the type-II 2HDM,the 125 GeV Higgs may have wrong-sign Yukawa couplings with down-type quarks.If such a Higgs acts as the portal between the DM and SM sectors,the model can give the isospin-violating interactions between DM and nucleons,which can relax the constraints from the DM direct detections.
A real singlet scalar S is introduced to the type-II 2HDM under aZ′2symmetry in which S→-S.The potential containing the S field is written as [35]

The S field has no vev and may serve as a DM candidate.The DM mass and the cubic interactions with the neutral Higgs bosons are obtained from equation (5.4),

In this model,the elastic scattering of S on a nucleon receives the contributions from the process with a t-channel exchange of h and H.The spin-independent cross section is written as [158],

A simple scenario is to take the 125 GeV Higgs (h) as the only portal between the DM and SM sectors.Iffqp≠fqn,the S-nucleon scattering may be isospin-violating for the appropriate values ofyhdandyhu.
The left panel of figure 5 shows that fn/fpapproaches to 1 with yd/yu.Namely,the S-nucleon scattering is isospin-conserving for yd=yuand significantly isospin-violating when yd/yudeviates from 1 sizably,especially since there is an opposite sign between ydand yu.The right panel shows that the bounds of the direct detection experiments can be satisfied in the region-1<fn/fp<0.8.The DM scattering rate with Xe target can be sizably suppressed for fn/fp~-0.7,which can weaken the constraints from the spin-independent DM-nucleon cross section.
There are other DM extensions of 2HDM which accommodate the DM direct detection limits.In the general 2HDM with a DM,when both h and H are portals between the SM sector and DM,and have appropriate couplings,the model can achieve the blind spots at DM direct detection,which originates from cancellations between interfering diagrams with h and H exchanges [47,48].Besides,in the L2HDM with a DM,the quark Yukawa couplings of H can be significantly suppressed for a very largetanβ.If such a H field is taken as the portal between the SM sector and DM,the model can easily weaken the bound of the DM direct detection and explain the muon g-2 [49,50].
6.Muon anomalous magnetic moment
6.1.L2HDM and muon g-2
The muon g-2 is a very precisely measured observable and serves as a sensitive probe of new physics (for a pedagogical review,see,e.g.[160]).The new Fermilab measurement[161]combined with E821 data[162]shows a 4.2σ deviation from the SM prediction [163–166].Such a discrepancy has been explained in various new physics models like minimal supersymmetry(see,e.g.[167–170]).Among the 2HDMs,the L2HDM can offer an explanation.
In the L2HDM,the lepton (quark) Yukawa couplings to H,A and H±can be sizably enhanced(suppressed)by a large tanβ.The model has been extensively studied to explain the muon g-2,and the searches at the LHC and low energy precision measurements can exclude a large part of parameter space for the explanation of muon g-2.The study in [19]considered the signal data of the 125 GeV Higgs,and found that the muon g-2 explanation favors the 125 GeV Higgs to have wrong-sign Yukawa couplings to the leptons.The experimental results of Br (Bs→μ+μ-) can exclude some parameter regions with a very light A [19].Besides,the measurements of lepton flavor universality (LFU) of the Z decays and τ decays give stringent constraints ontanβand the mass splittings among H,A and H±[20,24],and a more precise study was performed in [23].The muon g-2 explanation makes the additional Higgs bosons to have τ-rich signatures at the LHC,and the study in [21]first used the chargino/neutralino searches at the 8 TeV LHC to constrain the model.The analysis in [27]used the constraints of the multi-lepton analyses at the 13 TeV,and found that the L2HDM may explain the muon g-2 anomaly and produce a strong first order electroweak phase transition (SFOEWPT)simultaneously.
In the L2HDM,the additional contributions to the muon g-2 are mainly from the one-loop diagrams and the twoloop Barr–Zee diagrams mediated by A,H and H±.The oneloop contributions is given by [171–173]

where j=H,A,H±,Forrμj≪1 we have

For the main two-loop contributions,we have
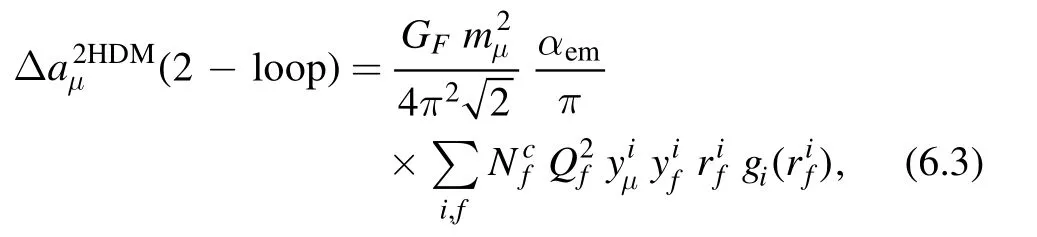
where i=H,A,and mf,QfandNfcare the mass,electric charge and the number of color degrees of freedom of the fermion f in the loop.The functions gi(r) are given by[174–176]

The contributions of H and A to Δaμare positive(negative)at the one-loop level and negative(positive)at the two-loop level.Sincemf2/mμ2easily overcomes the loop suppression factor α/π,the two-loop contributions can be larger than one-loop ones.As a result,the L2HDM can enhance the value of Δaμfor mA<mH.In [177]the authors presented an extension of the GM2Calc software to calculate the muon g-2 of 2HDM precisely.
Because of the large lepton Yukawa couplings,the L2HDM can give sizable corrections to the Z and τ decays,and thus be constrained by the measured values of LFU of the Z-boson [178]

and τ decays [179],

Here the first three ratios are defined as
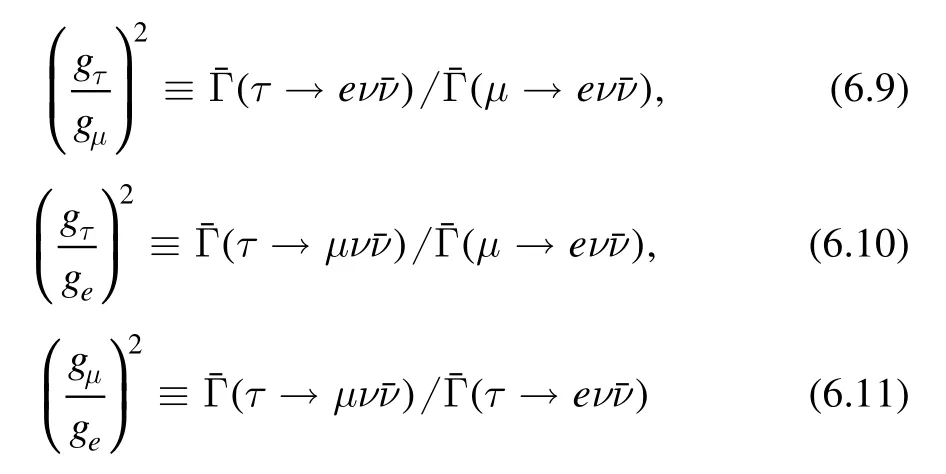
and the last two ratios are from semi-hadronic processes τ→π/Kν and π/K→μν.denotes the partial width normalized to its SM value.The correlation matrix for the above five observables is

The theoretical values of the ratios in the L2HDM are given as
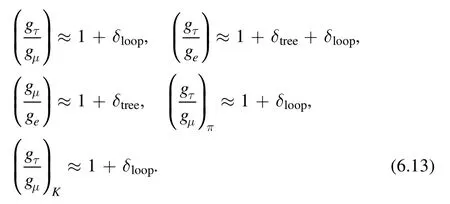
Here δtreeand δloopare respectively corrections from the treelevel diagrams mediated by H±and the one-loop diagrams involved H,A and H±[20,23]
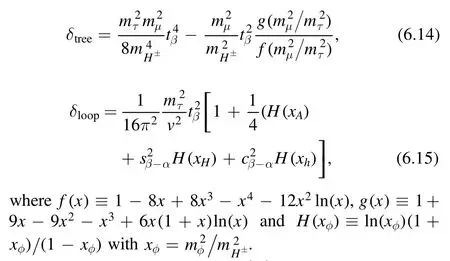
Under various theoretical and experimental constraints,the L2HDM can explain the muon g-2 anomaly in the regions of 32<tanβ<80,10 GeV<mA<65 GeV,260 GeV<mH<620 GeV,and 180 GeV<mH±<620 GeV.Because the contributions of A and H to the muon g-2 anomaly are respectively positive and negative,the mass splitting between A and H is required to be large to explain the muon g-2 anomaly,as shown in the lower-middle panel of figure 6.
The muon g-2 explanation requires a largetanβwhich will sizably suppress the quark Yukawa couplings of H,A and H±.Therefore,these extra Higgs bosons are dominantly produced at the LHC via the following electroweak processes:

The main decay modes of the Higgs bosons are
Therefore,in the parameter space favored by the muon g-2 explanation,the L2HDM will mainly produce a multi-lepton signature at the LHC,especially the multi-τ signature.
The study in [27]used all the analyses for the 13 TeV LHC in CheckMATE 2.0.7 [180]and the multi-lepton searches for electroweakino [181–185]to constrain the parameter space.The surviving samples are shown in figure 7 in which R >1 denotes that the corresponding samples are excluded at 95% confidence level.The searches for multileptons at the 13 TeV LHC shrink mAfrom [10,65]GeV to[10,44]GeV andtanβfrom [32,80]to [32,60].The main constraint is given by the search for electroweak production of charginos and neutralinos in multi-lepton final states[182].
For relatively large mHand mH±,the production cross sections of extra Higgs bosons are small enough to escape the limits of direct searches at the LHC.For a light A,the τ leptons from the decays of A produced in equations(6.16)and(6.17) are too soft to be distinguished at detectors,and the τ leptons from A produced in H/H±decays are collinear because of the large mass splitting between A and H/H±.Thus,in the very low mAregion,the acceptance of the above signal region quickly decreases and the limits of direct searches can be easily satisfied.
6.2.Solution of muon g-2 and τ decays
The L2HDM can give a simple explanation for the muon g-2,but raise the discrepancy in the LFU in τ decays.Therefore,to explain the muon g-2 and LFU of τ decays simultaneously,other models need to be considered.
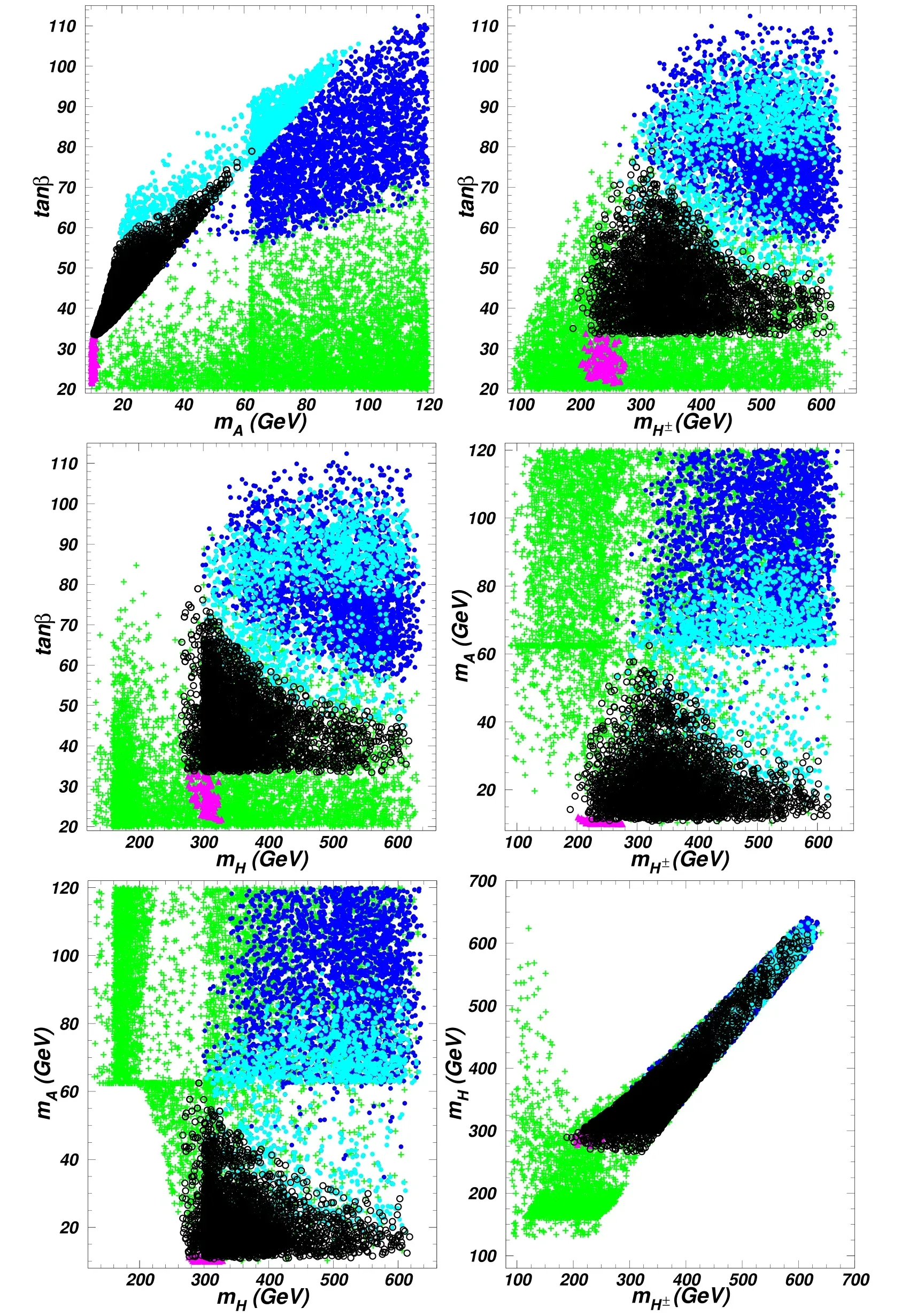
Figure 6.All the samples are allowed by the constraints of ‘pre-muon g-2’,taken from [27].The triangles (pink) are excluded by the Br(Bs→μ+μ-)data,and the light bullets(sky blue)and dark bullets(royal blue)are excluded by LFU in Z decay.The light(dark)bullets can(cannot) explain the muon g-2 anomaly.The circles (black) are allowed by the constraints from the muon g-2,‘pre-muon g-2’,the LFU in Z decay,and Br (Bs→μ+μ-).

Figure 7.All the samples are allowed by the constraints from the muon g-2,‘pre-muon g-2’,the LFU in Z decay,and Br(Bs→μ+μ-),taken from [27].The orange stars and green dots are excluded and allowed by the LHC Run-2 data at 95% confidence level,respectively.
6.2.1.Lepton-specific inert 2HDM.In this model the Z2symmetry-breaking lepton Yukawa interactions of Φ2are added to the inert 2HDM [186,187]

In this way the extra Higgs bosons (H,A,and H±) acquire couplings to the leptons while having no couplings to the quarks.

Here δtreeandare respectively corrections from the treelevel diagrams mediated by H±and the one-loop diagrams involving H,A and H±,given by [20,23,27]

The model gives the one-loop contributions to muon g-2 [171–173]

where i=H,A,H±and
The contributions of the two-loop diagrams are

where i=H,A,ℓ=τ,and mℓand Qℓare the mass and electric charge of the lepton ℓ in the loop.
This model was also used to discuss the electron g-2 anomaly,and the calculations are similar to the muon g-2.The value from the measurement of the fine-structure constant using133Cs atoms at Berkeley[188]makes the electron g-2 to have 2.4σ deviation from the SM prediction [189,190],

However,the newest experimental result of the fine-structure constant using87Rb atoms at Laboratoire Kastler Brossel gives a value of aewhich agrees well with the SM value[191].So far,the discrepancy between these two experimental results is not clear.If the Berkeley133Cs experiment result turns out to be the real story,it will be challenging to explain muon and electron g-2 simultaneously since the two effects have opposite signs.In [186],the Berkeley133Cs experiment data was used and this model was found to give an explanation for the muon and electron g-2 (for the explanation in other popular models like the minimal supersymmetry,see,e.g.[192]).
Taking

then δtreehas a positive value because of the opposite signs of кμand кτ.Thus,the model can enhanceand give a better fit to the data of the LFU in the τ decays.The contributions of H (A) to the muon g-2 are positive (negative) at the twoloop level and positive (negative) at the one-loop level.For the electron g-2,the contributions of H (A) are negative(positive) at the two-loop level and positive (negative) at the one-loop level.Figure 8 shows the surviving samples withχ2τ<9.72,which means to fit the data of LFU in τ decays within the 2σ range.Figure 8 shows thatχ2τcan be as low as 7.4,which is much smaller than the SM prediction (12.25).Figure 9 shows that after imposing the constraints of theory,the oblique parameters,the Z decay,and the direct searches at LHC,the model can simultaneously explain the anomalies of Δaμ,Δaeand LFU in the τ decay within the 2σ range in a large parameter space of 200 GeV<mH<320 GeV,500 GeV<mA=mH±<680 GeV,0.0066<кe<0.01,-0.25<кμ<-0.147,and 0.53<кτ<1.0.
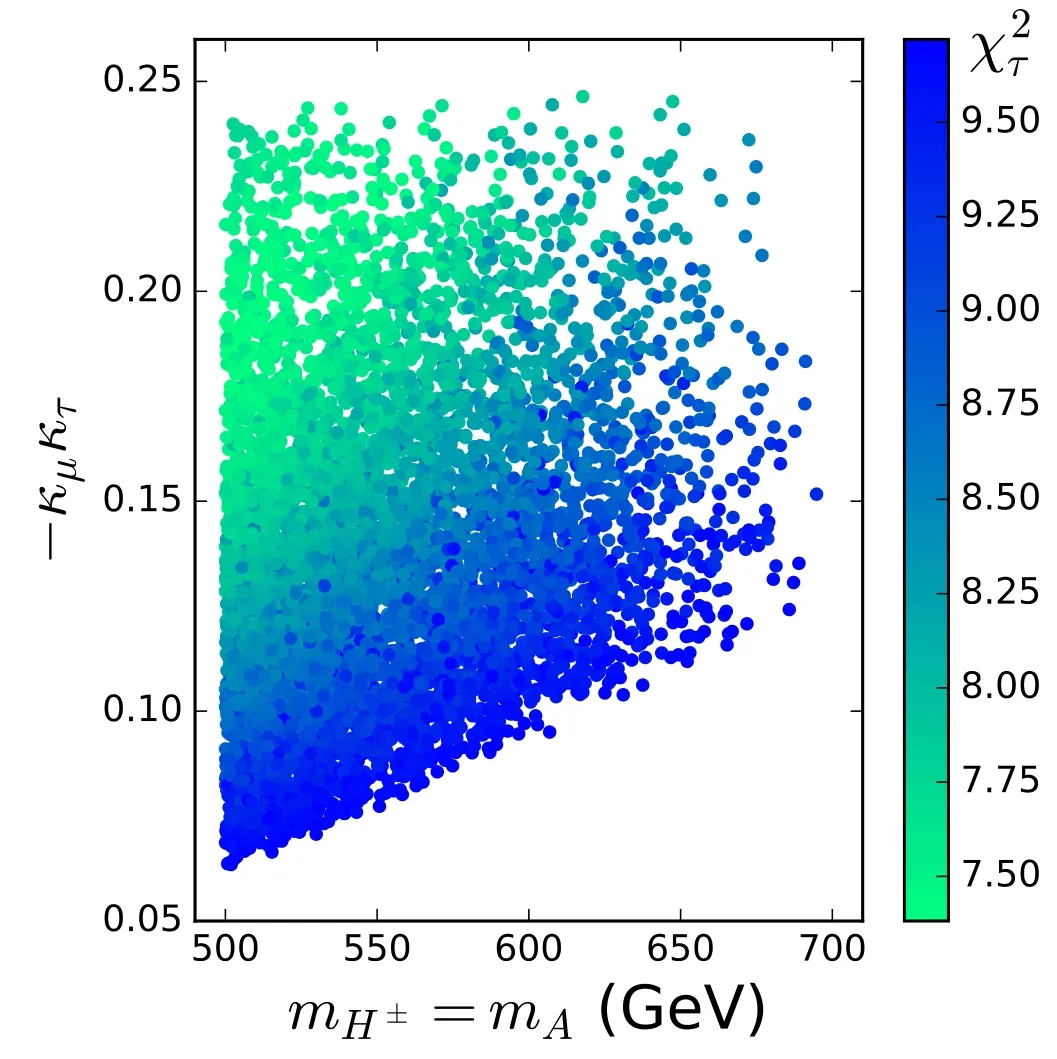
Figure 8.In the lepton-specific inert 2HDM,the surviving samples fit the data of LFU in τ decay within the 2σ range,taken from[186].
6.2.2.μ–τ-philic Higgs doublet model.In this model an exact discrete Z4symmetry is imposed,and the Z4charge assignment is shown in table 4 [193].The scalar potential is given as

The vev of the Φ1field is v=246 GeV,while the Φ2field has zero VeV.The fermions obtain masses via the Yukawa interactions with Φ1

The Z4symmetry allows Φ2to have μ–τ interactions [193]

From these interactions we can obtain the μ–τ lepton flavor violation (LFV) couplings of H,A,and H±.
The model gives a new contribution to Δaμvia the oneloop diagrams containing the μ–τ LFV coupling of H and A[194–196]

which shows that the contributions of H and A are respectively positive and negative.

where the flavor of final neutrino and anti-neutrino states is summed up,and δtreeis from the tree-level diagram mediated by the charged Higgs

Figure 10 shows that after considering the constraints from theory,the oblique parameters and the Z decay,the model can simultaneously explain Δaμand LFU in the τ decays in the parameter space with 300 GeV<mH<800 GeV and Δm<50 GeV.For such small mass splitting between mA(mH±) and mH,H,A and H±will mainly decay into τμ,τνμ,and μντ.The limits of direct searches at the LHC exclude the region mH<560 GeV and require ρ >0.68.Also[198,199]discussed the implications of the muon g-2 anomaly on the model.
In the discussions above,mAand±mHare chosen to have degenerate mass,which is disfavored by the CDF W-mass.The study in [59]found that combined with relevant theoretical and experimental constraints,the mass splittings among H,A and H±of the model are stringently constrained in the region simultaneously explaining the W-mass,muon g-2 and LFU in τ decays,i.e.10 GeV<mA-mH<75 GeV,65 GeV<mH±-mA<100 GeV,85 GeV<mH±-mH<125 GeV (-150 GeV<mH±-mA<-85 GeV,-105 GeV<mH±-mH<-55 GeV).

Figure 9.All the samples are allowed by the constraints of theory,the oblique parameters,Δaμ,Δae,the data of LFU in τ decays,and Z decay,taken from [186].The bullets and crosses are respectively allowed and excluded by the direct search limits from the LHC at 95%confidence level.The colors denote кτ,mA and mH in left,middle,and right panel,respectively.
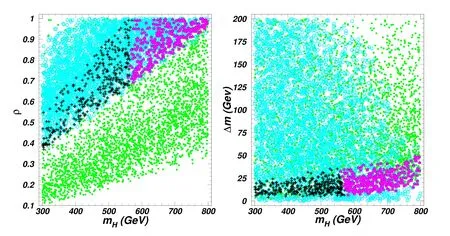
Figure 10.The surviving samples of the μ–τ-philic 2HDM allowed by the constraints of the theory,the oblique parameters,and the Z decays,taken from[197].The bullets(green)samples are within the 2σ range of muon g-2 and the circles(blue)are within the 2σ range of LFU in the τ decays.The triangles(purple)and pluses(black)are within the 2σ ranges of both muon g-2 and LFU in the τ decays,and the former are allowed by the limits of the direct searches at the LHC,while the latter are excluded.Here Δm ≡mA-mH with mA=mH±.
6.3.Other 2HDMs and muon g-2
In [200]the authors proposed a muon-specific 2HDM in which extra Higgs boson couplings to muon are enhanced by a factor oftanβ,while their couplings to the other fermions are suppressed bycotβ.Thus,the model can explain the muon g-2 anomaly by the contributions of the one-loop diagram for a very largetanβ,and weaken the constraints of the τ decays because of the cancellation oftanβbetween the tau and the muon Yukawa couplings to the charged Higgs.The study in[24]considered a perturbed lepton-specific 2HDM in which the sign of extra Higgs boson couplings to tau are flipped.Similar to the lepton-specific inert 2HDM,the model can accommodate the muon g-2 anomaly and the τ decays,but the electron g-2 anomaly is not simultaneously explained.The muon and electron g-2 anomalies can be both explained in general 2HDM.For recent studies see e.g.[201–203].
The L2HDM can be derived from the aligned 2HDM by taking the specific parameter space [14].Therefore,the aligned 2HDM may explain the muon g-2 anomaly in a broader parameter space,and the large lepton Yukawa couplings of A still play the main role in most of the parameter space [204].Some recent studies have been done in[205–209].In addition to the 2HDM with a Z4symmetry,the extra Higgs doublet with the μ–τ LFV interactions can be obtained in general 2HDM.For recent studies see e.g.[210–216].
7.Summary
From the above review we summarize the following points for the 2HDMs:(i)for the popular type-II 2HDM,the current direct searches at the LHC excluded a large part of parameter space,while still allowing the 125 GeV Higgs to have wrongsign Yukawa couplings to the down-type quarks and leptons.If a real singlet scalar DM is added to the type-II 2HDM and the 125 GeV Higgs with wrong-sign Yukawa couplings is taken as the portal between the SM sector and DM,this model can have isospin-violating interactions between DM and nucleons,which can relax the constraints from the DM direct detections;(ii) as a simpler DM model,in several DM mass ranges the inert 2HDM can produce the correct relic density and satisfy the bounds of DM direct detections and direct searches at the LHC;(iii) the muon g-2 anomaly can be explained in the lepton-specific 2HDM with a light A and heavy H/H±,but it will raise the discrepancy in the LFU in τ decays.Such a tension may be solved in the 2HDM with some specific muon and tau Yukawa couplings.So,compared with low energy supersymmetry (for recent reviews see,e.g.[217,218]),the 2HDMs can also do the job of explaining dark matter and muon g-2,albeit cannot address the naturalness problem.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (NNSFC) under grant Nos.11 975 013,11 821 505,12 075 300 and 12 105 248,by Peng-Huan-Wu Theoretical Physics Innovation Center (12047503),by the CAS Center for Excellence in Particle Physics (CCEPP),and by the Key Research Program of the Chinese Academy of Sciences,Grant NO.XDPB15.
 Communications in Theoretical Physics2022年9期
Communications in Theoretical Physics2022年9期
- Communications in Theoretical Physics的其它文章
- Preface
- Phase behaviors of ionic liquids attributed to the dual ionic and organic nature
- Chaotic shadows of black holes: a short review
- QCD at finite temperature and density within the fRG approach: an overview
- The Gamow shell model with realistic interactions: a theoretical framework for ab initio nuclear structure at drip-lines
- Effects of the tensor force on low-energy heavy-ion fusion reactions: a mini review
