Modelling drying pathways of an evaporating soft matter droplet
Guangle Du,Fangfu Ye,Hao Luo,Guangyin Jing,Masao Doi and Fanlong Meng
1 CAS Key Laboratory of Theoretical Physics,Institute of Theoretical Physics,Chinese Academy of Sciences,Beijing 100190,China
2 Wenzhou Institute,University of Chinese Academy of Sciences,Wenzhou 325001,China
3 School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China
4 Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China
5 Songshan Lake Materials Laboratory,Dongguan 523808,China
6 School of Physics,and State Key Laboratory of Photon-Technology in Western China Energy,Northwest University,Xi’an 710069,China
7 Center of Soft Matter Physics and its Applications,Beihang University,Beijing 100191,China
Abstract Micro-droplets of soft matter solutions have different morphologies upon drying,and can become wrinkled,buckled or cavitated particles.We investigate the morphology evolution of a drying soft matter droplet in this work:at the early stage of drying,wrinkling or cavitation instability can occur in the droplet,depending on the comparison between the critical wrinkling and cavitation pressure;at a later stage of drying,no wrinkles will appear if cavitation happens first,while cavitation can still occur if wrinkling happens first.A three-dimensional phase diagram in the space of elastic length,gel layer thickness and weight loss is provided to illustrate the drying pathways of a soft matter droplet.This diagram can help guide future fabrications of micro-particles with desired morphologies.
Keywords: soft matter solution,drying,instabilities
A soft matter droplet consisting of polymer solutions or colloidal dispersions can exhibit different morphologies such as buckling[1–4],wrinkling[5–8],or cavitation[9–12]during the drying process.When all solvents evaporate,the soft matter droplets can turn out to be solid,hollow,wrinkled or buckled particles as the final products [13–17].This drying process,especially spray drying,has been widely utilised to produce micro-particles of different morphologies in industrial circumstances such as food or pharmaceutical particle production[17–21],amorphous material crystallisation[22–24],functional encapsulated particle manufacture[25–27],etc.,where different shapes are achieved by empirically changing the drying temperature,concentration and constitution of the soft matter solution [3,28–36].
In the drying process of a soft matter droplet,the competition of solute advection towards the droplet surface as the deposition due to drying and solute diffusion homogenising the solute concentration is captured by the Péclet number.When the Péclet number is sufficiently large,the solution at the outmost layer of the droplet can solidify to become a gel-like layer[16,37–39],which grows with time.This gel layer has been believed to relate to the morphology evolution and the final configurations of drying soft matter droplets [12,33,40–42].However,how the properties of the gel layer can determine the drying process of the soft matter droplet still remains unclear.
In this work,we will study how the morphology of a drying soft matter droplet can evolve with time depending on the physical properties of the gel layer such as its elasticity and dimension,by considering the prepared state of the droplet as a spherical core–shell structured system as in spray drying(shown in figure 1).The core will be simply regarded as liquid,whose amount decreases continuously due to solvent evaporation;the shell(skin layer)will be treated with non-evolving elastic properties and thickness for simplicity,as the evolution of the skin layer,such as mass growth from further diffusion and deposition of the solute,would not change the results qualitatively.By taking these simplifications,we can construct the analytical energy form of the system,and then discuss the morphology evolution of the drying soft matter droplet.

Figure 1.Drying pathways of an evaporating soft matter droplet.
Compared to solvent evaporation,the mechanically equilibrating process of the gel layer is a fast process;in other words,we can use the mass loss of the droplet due to evaporation,ΔW=W0-W,as the controllable variable of the system,where W0and W denote the initial and current mass of the droplet,respectively.Then we can discuss the morphology evolution of the droplet by optimising the total free energy of the system under given ΔW.By taking the initial radius of the droplet as R0,and the radius of the cavity as Rc[reduced cavity volumevc≡(RcR0)3],the volume of the droplet can be expressed asfrom volume conservation.The total Gibbs free energy of the system can be written as
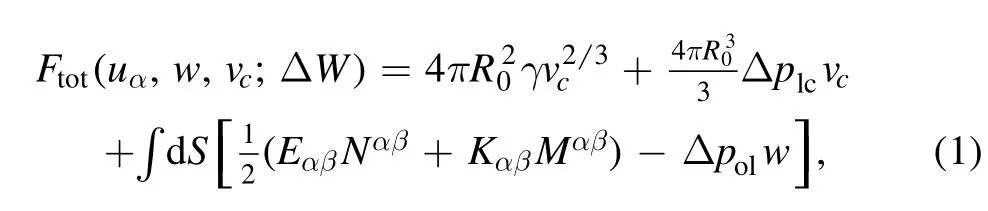
where γ denotes the interfacial tension between the cavity and the fluid,Δpol=po-pland Δplc=pl-pc,with po~105Pa,pland pcas the pressure of the outside,the liquid and the cavity,respectively.The pressure of the cavity can be expressed as8See supplementary materials available online at stacks.iop.org/CTP/74/095605/mmedia.where vlis the volume of a single liquid molecule,PL(x)is the principal branch of Lambert W function and peqis the bulk vapor pressure.Taking typical values of vl~10-29m3and peq~105Pa,we have peqvl/(kBT)~10-3,and then the pressure in the cavity can be approximated bypc≈peqexp [-2γ vl/(RckBT)].In equation(1),the first term on the right-hand-side(RHS)denotes the interfacial energy of the interface between the cavity and the liquid,the second term denotes the work done by the pressure difference between the liquid and the cavity,and the last term denotes the elastic energy of the gel layer.In the last term,Eαβand Kαβare the stretching and the bending strains,respectively,Nαβand Mαβare the stretching stress and the bending moment,respectively,w is the normal displacement along the radial direction of the gel layer.Note that the normal displacement is taken as positive if it is pointing towards the droplet centre.Here we adopt the Donnell–Mushtari–Vlasov (DMV) strain-displacement relations,which are valid for small deformations,as Eαβ=(∇βuα+∇αuβ)/2-bαβw+∂αw ∂βw/2 and Kαβ=∇α∇βw,where ∇is covariant derivative,uαis the tangential displacement along α direction and bαβis curvature tensor of the gel layer shell [43].The stretching stress Nαβand the bending moment Mαβcan be expressed as functions of the strain tensors:Nαβ=Eh[(1-ν)Eαβ+νgαβEγγ]/(1-ν2) andMαβ=Eh3[(1-ν)Kαβ+νgαβKγγ]/[12 (1-ν2)],with gαβbeing the metric tensor of the shell surface,and h,E and ν being the thickness,Young’s modulus and the Poisson ratio of the gel layer,respectively [43].
Critical wrinkling pressure.The gel layer can wrinkle or buckle during the drying process,and we first discuss the criterion of when wrinkling or buckling can occur on the surface of the droplet.If there is no cavity,the total energy reduces to the purely elastic one (last term on the RHS of equation (1)).To obtain the critical wrinkling pressure,we perform the linear instability analysis on the Euler–Lagrange (EL) equations obtained from the variation of the elastic energy functional(see footnote 8).The uniform solution of the EL equations is uφ=uθ=0,w0=(1-ν) ΔpolR02/(2Eh),which represents the uniform contraction of the gel layer under the pressure difference between the outside and the liquid Δpol.By adding a small perturbation w1to the uniform normal displacement,i.e.,w=w0+w1and introducing a small perturbation χ1in the Airy stress function [43],we can obtain
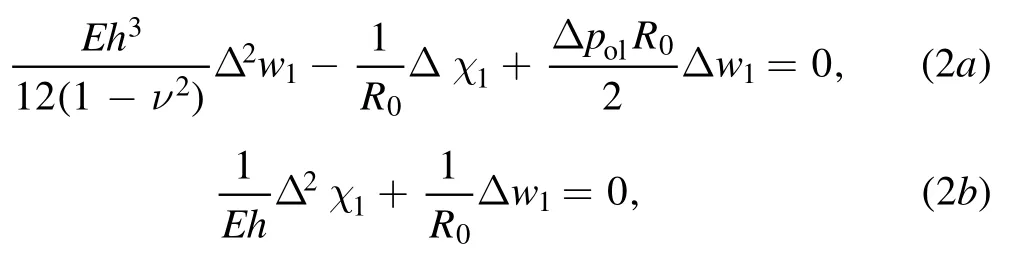
after keeping terms up to the linear order in the EL equations.By expressing w1and χ1with spherical harmonicsYlm(φ,θ)(eigenmodes of Laplace operator),asw1=AYlmandχ1=BYlm,then from equation (2) we can obtain the possible eigenmodes denoted by l as a function of the pressure Δpol,

where D=Eh3/[12(1-ν2)].The minimal pressure Δpoldenoted by *pwto have a real and positive l(l+1),i.e.,the critical pressure leading to wrinkling,is [43]

It is clear that the gel layer can easily wrinkle if it is soft(small Young’s modulus) and the thickness is small compared to the droplet size.If there is a ring-like defect with a smaller Young’s modulus in the gel layer,then buckling can easily occur and the corresponding buckling pressure can be obtained by shallow shell approximation,which gives the same value as the critical wrinkling pressure *pw(See footnote 8).Note this critical wrinkling pressure is obtained for a perfect sphere and is sensitive to imperfections [44,45].If imperfections are present in shell possibly due to density inhomogeneity [46],orthotropic elasticity [47],etc.,the critical wrinkling pressure can drop considerably by an empirical proportion.Nevertheless,the above critical wrinkling pressure can still dominate the wrinkling behavior.In the following discussions,we use the term‘wrinkling instability’ to denote both wrinkling and buckling instability without losing generality.
Critical cavitation pressure.There is a critical cavitation pressure *pcif there is no wrinkling.In this case,the elastic energy of the gel layer is simplyFelastic=12πhKew02[41],where Ke=E/[3(1-ν)]is the effective elastic modulus.After the insertion of the mass conservation relation,the total Gibbs free energy of the system is
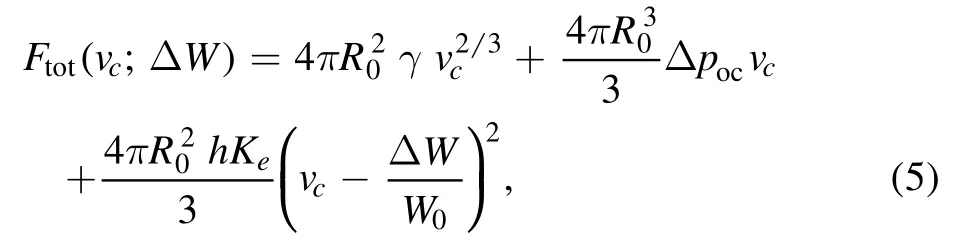
where Δpoc=po-pc.The critical point for the above total Gibbs free energy to have a non-zero local minimum point is determined by ∂Ftot/∂vc=0 and Ftot(vc)=Ftot(0),from which we can obtain the critical cavity volume asvc*=[le(2h)]3/4with the elastic length defined by le≡2γ/Keand the critical weight loss for cavitation as[41].Utilisation of the mass conservation under uniform contraction with no cavity gives the relation between the pressure and the weight loss Δpol=2hKe/R0·ΔW/W0.Then the critical cavitation pressure,i.e.,the minimal pressure Δpoldenoted by*pcto have cavity,is

By comparing the critical wrinkling pressure *pwand the critical cavitation pressure *pc,we can obtain the criterion for wrinkling happening ahead of the droplet cavitation at an early stage of the drying process,written explicitly as

otherwise,cavitation occurs first.In other words,if the gel layer is thin and soft,the droplet tends to wrinkle at the surface.More importantly,such divergence in the instabilities at the early stage of the drying process leads to different drying pathways and can determine the final morphology of the drying droplet as discussed below.
Drying pathway–no wrinkling after cavitation.We investigate whether wrinkling still occurs if cavitation happens first.As shown in the inset of figure 2(b),Δpolconstantly increases before cavitation and becomesafter cavitation.At the critical cavitation point,which is smaller than the critical cavitation pressure *pc.Meanwhile,the first derivative of Δpolafter cavitation with regards to the weight loss,∂Δpol/∂ΔW=-2γ/(R0W0)means that Δpoldecreases further with increasing weight loss ΔW.This indicates that no wrinkling can happen after cavitation since the critical wrinkling pressure can not be reached any more [drying pathway in figure 1 as (a)→(b)→(c1)→(c2)].
Drying pathway–cavitation after wrinkling.We proceed to investigate whether the cavity can still form if wrinkling occurs first.By assuming the wrinkles as a perturbation with the form of a spherical harmonic mode and assuming that the perturbation amplitude is small,then the Helmholtz free energy can be expressed in the same form as that in equation (5),but with a modified effective elastic modulus(see footnote 8)

whereA′=A/his the ratio of the perturbation amplitude over the gel layer thickness.Then it is clear that cavitation can still happen after wrinkling,with the critical weight loss for cavitation aswhereis the new elastic length.Meanwhile,the effective elastic modulusKe′ is smaller than the one without wrinkling Ke,resulting in a larger value of the critical weight loss than that in the case without wrinkling.Note that according to the previous discussion,the pressure difference between the outside and the liquid Δpoldrops at cavitation and decreases after cavitation with the increase of weight loss (see inset of figure 2(b)),thus the wrinkles may disappear due to the decrease of Δpol.However,in a practical drying process,the formed wrinkles of the gel layer can become rigid,e.g.turn glassy [40],and the decrease of Δpolinduced by the cavitation is not high enough to flatten the wrinkles on the gel layer with increased rigidity.In this case,the wrinkles can still remain regardless of the decrease of the pressure difference between the outside and the liquid after cavitation (drying pathway in figure 1 as(a)→(b)→(d1)→(d2)).Note that the gel layer can still be permeable to solvents despite its rigidification,and the subsequent evaporation and cavity enlargement are not hindered.
In figure 2(a),a 3D phase diagram summarising the above discussions of the drying pathways of a soft matter droplet is provided in the space of elastic length,gel layer thickness and weight loss,together with its two cross sections of a given fixed elastic length in figure 2(b) and of a given fixed thickness in figure 2(c),respectively.Note that the weight loss in the phase diagram can play the role of time if the evaporation rate of the droplet is known [39,48].At the early stage of the drying process,i.e.,when ΔW is small,either wrinkling or cavitation instability can occur,resulting from the competition between the surface energy of the cavity,and the bending and stretching elastic energy of the gel layer.When the gel layer is thin and soft(small h and small Ke(large le)),then wrinkling occurs,which is obvious in figure 2(b) and figure 2(c);otherwise,cavitation happens.Meanwhile,the choice in either wrinkling or cavitation instability at the early stage of the drying process,determines the later morphology evolution and the final product of the drying soft matter droplet: (a) if wrinkling takes place ahead of the cavitation,then there will still be cavity formed in the droplet with the ongoing evaporation of the solvents and the final configuration of the drying droplet will be a hollow and wrinkled particle;(b)if cavitation happens first,then there will be no wrinkling in the later drying process due to the decreasing pressure difference between the outside and the droplet,and a spherical shell is left after finishing the whole evaporation process.
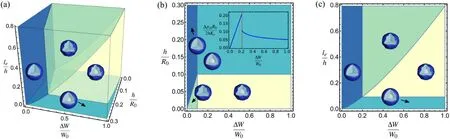
Figure 2.(a)3D phase diagram with three dimensionless varying variables,i.e.,elastic length over shell thickness le/h,shell thickness over initial droplet radius h/R0,and the reduced weight loss of the droplet ΔW/W0.Here Poisson ratio ν=0.5.(b) Cross section of 3D phase diagram with fixed le/h=0.037.Inset: the pressure difference between the outside and the liquid is smaller than the critical cavitation pressure and constantly decreases after cavitation,impeding the occurrence of wrinkling.In the inset,le/h=0.1.(c) Cross section of 3D phase diagram with fixed h/R0=0.2.
We investigate here how the morphology of a drying soft matter droplet can evolve with time based on a pseudo-dynamic analysis.The elastic properties of the gel layer formed at the surface of the soft matter droplet play a key role in determining the drying pathways of the droplet,including both the instabilities triggered at the early stage of the drying process,the later morphology evolution,and the final configurations.A quasiequilibrium treatment is taken for discussing how morphology of a droplet evolves with time by performing energy minimisation,which at certain conditions should be revised,e.g.,if the evaporation is fast where sub-processes such as solute diffusion,gel-layer formation,etc occur at a comparable time scale as solvent evaporation.Regardless of the simplifications for analytic discussions in this work,we believe this portable model has captured the essential physics underlying the morphology evolution of a drying soft matter droplet,which can guide the industrial fabrications of micro-particles with desired morphologies and functions.
Acknowledgments
F M acknowledges supports from Chinese Academy of Sciences (No.XDA17010504 and No.XDPB15),and the National Natural Science Foundation of China (No.12 047 503).F Y acknowledges the support of the National Natural Science Foundation of China(Grant No.11 774 394)and the Key Research Program of Frontier Sciences of Chinese Academy of Sciences(Grant No.QYZDB-SSW-SYS003).G D thanks Xiao Lin for fruitful discussions.
ORCID iDs
 Communications in Theoretical Physics2022年9期
Communications in Theoretical Physics2022年9期
- Communications in Theoretical Physics的其它文章
- Vector semi-rational rogon-solitons and asymptotic analysis for any multicomponent Hirota equations with mixed backgrounds
- High precision solutions to quantized vortices within Gross–Pitaevskii equation
- Quantum dynamics of Gaudin magnets
- Realizing number recognition with simulated quantum semi-restricted Boltzmann machine
- A prototype of quantum von Neumann architecture
- PV-reduction of sunset topology with auxiliary vector
