Application of kernel ridge regression in predicting neutron-capture reaction crosssections

T X Huang,X H Wuand P W Zhao

State Key Laboratory of Nuclear Physics and Technology,School of Physics,Peking University,Beijing 100871,China

Abstract This article provides the first application of the machine-learning approach in the study of the crosssections for neutron-capture reactions with the kernel ridge regression(KRR)approach.It is found that the KRR approach can reduce the root-mean-square(rms)deviation of the relative errors between the experimental data of the Maxwellian-averaged(n,γ)cross-sections and the corresponding theoretical predictions from 69.8%to 35.4%.By including the data with different temperatures in the training set,the rms deviation can be further significantly reduced to 2.0%.Moreover,the extrapolation performance of the KRR approach along different temperatures is found to be effective and reliable.

Keywords: kernel ridge regression,machine learning,neutron-capture reaction

1.Introduction

Nuclei are complicated many-body quantum systems consisting of nucleons,and the scope of nuclear physics study ranges in size from the lightest nuclei formed in the big bang to the nuclear matter in the interior of neutron stars.During the past decades,great efforts and achievements have been made in the measurements of various properties of nuclei,and currently about 3000 nuclei have been observed in the laboratory [1].However,there are still a large number of nuclei remaining unknown from experiments.What’s more,even for the experimentally known nuclei,many properties that are crucial in understanding both the nuclear structure and the origin of the elements,are still beyond the experimental capability.Therefore,reliable theoretical descriptions of nuclear properties are imperative at the present time.

Precise theoretical description of nuclear properties has been a longstanding challenge of nuclear physics,due to the difficulties in understanding both the nuclear interactions and the quantum many-body systems.In principle,an exact theoretical description of nuclear properties should be obtained by solving the Schrödinger equation for all constituent nucleons and the interactions between them,i.e.ab initiocalculations.This can be done exactly only for the lightest nuclei up toA=3,4[2–5]and become applicable to light and medium-mass nuclei up to aboutZ=50 [6,7]with some approximations.Currently,the density functional theory(DFT)is the only tool that can provide global descriptions for nuclei in the whole nuclear chart[8–13].In particular,in a recent work [11],the nuclear landscape has been investigated within the triaxial relativistic density functional theory with the PC-PK1 [14]functional,and the beyond-meanfield dynamical correlation energies are taken into account by a microscopically mapped five-dimensional collective Hamiltonian without additional free parameters.Nevertheless,the precisions of DFTs are still required to be improved,especially for the cases that the functional cannot be well constrained,e.g.properties of exotic nuclei far from the experimentally known region and the high-density nuclear matter in neutron stars.The uncertainties of nuclear properties would limit our understanding of exotic nuclear structure and astrophysical nucleosynthesis [15,16].Therefore,seeking effective ways to further improve nuclear theories for predicting various nuclear properties is one of the most important frontiers of nuclear physics.

Over the past decades,increasingly powerful computers and continuously optimizing algorithms have driven explosive applications of machine learning(ML)in many fields of physics[17],including nuclear physics[18].Some of the ML applications in nuclear physics focus on rebuilding or refining the nuclear theory itself,e.g.applications in nuclear energy density functionals [19],variational calculations [20,21],extrapolations for many-body physics [22–25],etc.Other applications focus on improving the description accuracies of nuclear properties from existing nuclear theory,e.g.applications in nuclear masses[26–33],β-decays [34,35],charge radii [36–38],excited states[39–41],fission yields[42,43],spallation reactions [44,45]and projectile fragmentation reactions [46,47],etc.The applications of various ML approaches to various aspects of nuclear physics can be found in a recent review[18].Here,we would focus on the applications of kernel ridge regression(KRR)in nuclear physics.

The KRR is a powerful machine-learning approach,which extends ridge regression to the nonlinear case by learning a function in a reproducing kernel Hilbert space [48–50].The KRR approach was firstly introduced to the field of nuclear physics to improve nuclear mass predictions [31]in 2020.It is found that the KRR approach can avoid the risk of worsening the mass predictions for nuclei at large extrapolation distances[31],and has obtained the most precise machine-learning mass model so far when the odd–even effects are taken into account[33].The successful applications of the KRR approach in nuclear masses have also triggered more applications including the ML energy density functionals [19]and charge radii [51].

Neutron-capture reaction plays a significant role in the cosmic nucleosynthesis of elements heavier than iron,through thes-andr-processes [52–54].In thes-process,the neutroncapture rates,especially for thes-process branch-point nuclei,are crucial fors-abundances determination,by affecting thes-process path and the reaction flow along the path [53].In ther-process,the neutron-capture rates affect ther-abundances by controlling the speed of therprocess as well as the location of ther-process path [55].Experimentally,the data of neutroncapture reaction cross-sections are available only for about 300 nuclei [56].Theoretically,the neutron-capture reaction crosssections are mainly predicted by the Hauser–Feshbach statistical model [57],and the corresponding uncertainty is about a factor of three for stable nuclei [58],and becomes much larger for unstable ones [15].The difficulties in experiments and the uncertainties in theories limit the stellar nucleosynthesis simulations of thes-process andr-process.It is thus in demand to further improve the prediction accuracies of neutron-capture reaction cross-sections.The present work provides the first ML application in the neutron-capture reaction study,by applying the KRR approach to improve the Hauser–Feshbach predictions.

The paper is organized as follows.In section 2,the theoretical framework of the KRR approach is presented.In section 3,the numerical details are given.Then,the results of the KRR application in neutron-capture reaction cross-sections are presented in section 4.Finally,a summary is given in section 5.

2.Theoretical framework

The typical neutron spectrum of the variouss-process andr-process sites is described by a Maxwell–Boltzmann distribution,because neutrons are quickly thermalized in the dense stellar plasma.The effective stellar reaction crosssections are thus obtained as the Maxwellian-averaged(n,γ)cross-sections (MACS)

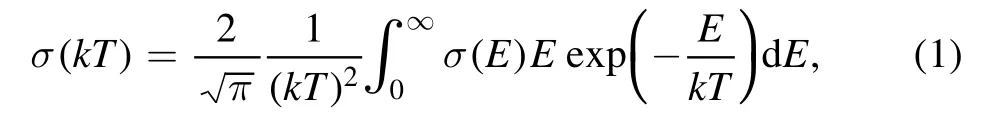
wherekTis the environment temperature andσ(E) is the ground state neutron-capture cross-section at a specific relative kinetic energyE.Experimentally,due to the difficulties in making targets with unstable nuclei,currently the MACSs are only available for about 300 nuclei around the stable line in the temperature range fromkT=5 keV to 100 keV [56,59].Theoretically,the MACSs adopted in the stellar nucleosynthesis simulations are mainly obtained by the Hauser–Feshbach statistical model(HFSM)[57].However,the predictions of the HFSM with different model inputs,e.g.nuclear level densities andE1 gamma-ray strength functions,can vary with a factor of three for nuclei around the stable line [58],and the model variations can be much larger for nuclei away from stability[15].The present work introduces the KRR approach to improve the Hauser–Feshbach predictions of MACS.

The logarithmic residual of MACS for the nucleus(Zj,Nj)at temperatureTjin the KRR approach is expressed as

where the kernel function is taken as

The logarithmic deviation(Z,N,T)in the KRR approach is trained to reconstruct the logarithmic residual of MACS between experimental data 〈σ〉exp(Z,N,T)and theoretical predictions 〈σ〉th(Z,N,T),i.e.Δ(Z,N,T)=The weightsωiare determined by minimizing the loss function defined as

whereω=(ω1,...,ωm).The frist term represents the variance between data and KRR prediction,and the second term is a regularizer that penalizes large weights to reduce the risk of overfitting.Minimizing loss functionL(ω)in equation(4)yields

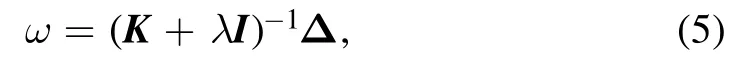
whereKis the kernel matrix with elementsKij=K(xi,xj),Iis the identity matrix,and Δ=(Δ1,...,Δm)are the data to be learned.

Once the reconstructed KRR function(Z,N,T)is obtained,the KRR prediction of MACS can be given by

There are two main differences between the present KRR scheme for MACS and the one for nuclear masses [31,33].One is that the temperature is also included as an input,so a new hyperparameterηshould be additionally introduced.The other one is that the KRR function is trained to reconstruct the logarithmic residual of MACS because the MACS values vary by several orders of magnitude for different nuclei.

3.Numerical details

In the present work,the experimental MACS data for 242 nuclei withZ＞ 20 are taken from Karlsruhe Astrophysical Database of Nucleosynthesis in Stars (KADoNiS) v1.0 [56].For each nucleus,MACS data at twelve temperatures(kT=5,8,10,15,20,25,30,40,50,60,80,100 keV)are available.

Theoretical MACSs are calculated by the HFSM with the Talys program [60,61],which depends on the inputs including the level density models and theE1 gamma-ray strength functions.We employ 6 level density models and 8E1 gamma-ray strength functions,and thus have 48 combinations in total.The 6 level density models include constant temperature+Fermi gas model (CTM) [62],back-shifted Fermi gas model (BFM) [62],generalised superfluid model (GSM) [62],microscopic level densities (Skyrme force) from Goriely’s tables (HFBCS) [63],microscopic level densities (Skyrme force) from Hilaire’s combinatorial tables (HFB) [64],and microscopic level densities(temperature dependent HFB,Gogny force) from Hilaire’s combinatorial tables (T-HFB) [65].The 8E1 gamma-ray strength functions include Kopecky-Uhl generalized Lorentzian (KUGL)[66],Brink-Axel Lorentzian(BAL)[67,68],Hartree–Fock BCS tables (HFBCS) [69,70],Hartree–Fock–Bogolyubov tables(HFB) [69,71],Goriely’s hybrid model (GHM) [72],Goriely T-dependent HFB (T-HFB) [60],T-dependent RMF (T-RMF)[60],and Gogny D1M HFB + QRPA (D1MHFB) [60].Other inputs are taken as the default settings of the Talys1.9 [60,61].

The involved hyperparameters in the KRR approach,i.e.penalty strengthλ,andσandηthat appear in the kernel function,are determined through the leave-one-out cross-validation(LOOCV).

4.Results and discussions

We first focus on the study of MACS at a specific temperaturekT=30 keV,which is a typical temperature in thes-process environment [73].As the HFSM calculations are carried out with 48 groups of level density models and strength functions,we introduce 48 KRR networks,which are trained with the logarithmic deviations between the experimental MACS data and the 48 sets of theoretical predictions respectively.For each network,the KRR hyperparameters are optimized with the lowestΔrmsthrough the leave-one-out cross-validation(LOOCV).

Figure 1.The rms logarithmic deviations Δrms of the Talys and the KRR predictions with respect to the experimental MACS data.

In figure 1,the rms logarithmic deviationsΔrmsof the Talys and the KRR predictions with respect to the experimental MACS data are depicted.The rms logarithmic deviations for the Talys results are generally around Δrms=0.25,which refers to a relative deviation of 78%.Specifically,theΔrmsobtained with the level density model GSM is relatively large,and theΔrmsobtained with the strength functions HFBCS and HFB are relatively small.Nevertheless,the KRR approach improves the Talys predictions in all cases.The rms logarithmic deviations are generally reduced to below0.20 by the KRR approach,and can even reach to below 0.13 for several cases.In particular,for the Talys calculations with the level density model CTM and strength function HFBCS,the KRR approach provides the smallest rms logarithmic deviation0.116,which refers to a relative deviation of 31%.So,the following analyses will be based on this case.

In figure 2,a detailed comparison of the KRR predictions and the Talys calculations with the level density model CTM and the strength function HFBCS is illustrated,where the modified relative error (MRE)δis introduced as

It refers to a deviation from 100% for the ratio between the prediction values and data.The MREsδbetween the Talys predictions and the experimental data are mainly in the range from 0 to 2,and the corresponding rms deviation ofδ(δrms) is 69.8%.For the KRR predictions,the corresponding MREsδare reduced mainly in the range from 0 to 1,and this corresponds to a rms deviation of35.4%.Moreover,the KRR approach improves the predictions of the MACS globally for nuclei in different mass regions.

To illustrate the potential impacts of the present KRR predictions of the MACS on the s-process simulations,in figure 3,the KRR predictions of the MACSs for 21 s-process branch-point nuclei [53]scaled by the Talys predictions are depicted.Among these 21 nuclei,experimental data of MACSs are available for eight of them.In comparison with the Talys calculations,the KRR approach improves the predictions for 6 of the 8 nuclei,and worsens the predictions only for 2 ones,i.e.163Ho and171Tm.Note that the experimental data of171Tm have been updated by recent experiments[74],which are displayed with stars in figure 3 and match the KRR predictions better than the old data.These results suggest that the KRR predictions of the other 13 s-process branch-point nuclei,whose experimental values of the MACSs are unavailable,can be trusted.This would lead to positive influences on the s-process simulations.To see the effects of the KRR corrections of the MACS on the s-process simulations would be interesting in future work.

Figure 2.The MREsδ (see text) of the Talys and the KRR predictions with respect to the experimental MACS data.

Figure 3.The KRR predictions of the MACSs for 8 s-process branch-point nuclei with available experimental data(solid diamond)and 13 ones without experimental data (hollow diamond) scaled by the Talys predictions.The experimental values [56]are denoted by black dots when they are available.For 171Tm,two latest experimental data from[74]are also displayed with stars,which are measured with the activation method and the time-of-flight method,respectively.The grey line represents the Talys calculations.

To include the temperature degree of freedom,it should be noted that the MACS dependence on temperature is quite different from that on the proton and neutron numbers.To carefully study the temperature effects,here we introduce two kinds of LOOCV to validate the KRR approach.The first one is called the leave-one-data-out-cross-validation(LODOCV),which means that when predicting the MACS labeled by(Z,N,T),only the MACS data of the nucleus(Z,N)at temperatureTis removed from the training set.The other one is called the leave-one-nucleus-out-cross-validation(LONOCV),which means that when predicting the MACS labeled by(Z,N,T),all the MACS data of the nucleus(Z,N)are removed from the training set.

Figure 4(a) depicts the rms MREδrmsof the KRR predictions with respect to the experimental MACS data at different temperatures through the LODOCV and LONOCV respectively,in comparison with the Talys results.As can be seen,the KRR predictions with both LODOCV and LONOCV can improve the Talys predictions at all the temperatures,and the improvement of LODOCV is much more significant than that of LONOCV.This indicates that the MACS data of a nucleus at different temperatures can help to predict each other,as the MACS data with different temperatures for the target nucleus are involved in the training set in the LODOCV.

A detailed comparison between the MREsδfor the KRR predictions atkT=30 keV is given in figure 4(b).The improvement achieved by the KRR predictions with LODOCV is significant in the whole mass region,and the correspondingδrmsis as small as2.0%.Nevertheless,the improvement achieved by the KRR predictions with LONOCV is just similar to the learning results without temperatures [see figure 2(a)],and the correspondingδrmsis 35.7%.Therefore,to predict the MACS for a nucleus(Z,N)at a specific temperatureTin the KRR approach,the MACS data for the same nucleus(Z,N)at different temperaturesTare most helpful.

In order to examine the extrapolation power of the KRR approach along different temperatures,the KRR network is trained with the MACS data for all nuclei only at the temperatureskT=25 and30 keV,and the corresponding KRR predictions for the MACS at all temperatures are displayed in figure 4(c) in comparison with the Talys results.The KRR approach improves the predictions at all temperatures.The improvements are significant when the temperatures are close to the training temperatureskT=25 and30 keV,and are still quite considerable even when the temperatures are far from the training temperatures.This indicates the reliability in extrapolating the MACS predictions along different temperatures in the KRR approach.

5.Summary

Advances in machine-learning methods have driven explosive applications in nuclear physics.The kernel ridge regression(KRR) is a powerful machine-learning approach,which extends ridge regression to the nonlinear case by learning a function in a reproducing kernel Hilbert space.Recently,it has been introduced in the field of nuclear physics,and achieved many successes in building nuclear energy density functionals and predicting nuclear properties including nuclear masses,radii,etc.This article provides the first application of the machine-learning approach in the study of the cross-sections for neutron-capture reactions with the KRR approach.It is found that the KRR approach can reduce the root-mean-square deviation of the relative errors between the experimental MACS data and the theoretical predictions from 69.8% to 35.4%,and thus can help to improve the MACS predictions ofs-process branch-point nuclei.By including the MACS data with different temperatures in the training set,the rms deviation can be further reduced to 2.0%.Moreover,the extrapolation performance of the KRR approach along different temperatures is found to be effective and reliable.

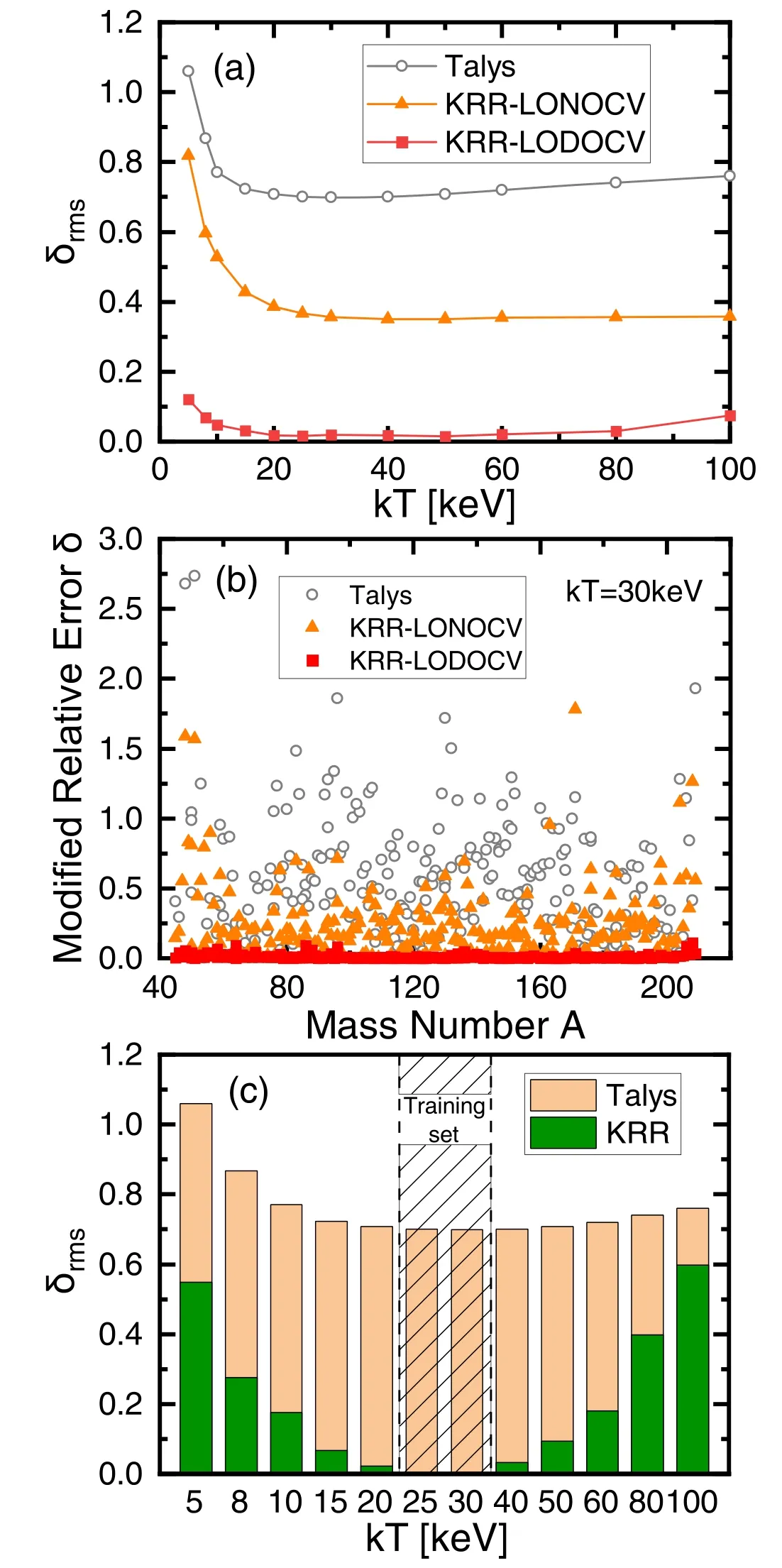
Figure 4.(a) The rms MREδrms of the Talys and the KRR predictions with respect to the experimental MACS data at different temperatures.(b) Theδ of the Talys and the KRR predictions with respect to the experimental MACS data atkT=30 keV.(c) The extrapolation of the KRR approach along different temperatures in comparison with the Talys results.The shadowed area denotes the training data (see text).

Acknowledgments

This work was partly supported by the National Key R&D Program of China (Contracts No.2018YFA0404400 and No.2017YFE0116700),the National Natural Science Foundation of China(Grants No.11875075,No.11935003,No.11975031,No.12141501 and No.12070131001),the China Postdoctoral Science Foundation under Grant No.2021M700256,and the Highperformance Computing Platform of Peking University.