The dynamical holographic QCD method for hadron physics and QCD matter

Yidian Chen,Danning Li and Mei Huang

1 School of Nuclear Science and Technology,University of Chinese Academy of Sciences,Beijing 100049,China

2 Department of Physics and Siyuan Laboratory,Jinan University,Guangzhou 510632,China

Abstract In this paper we present a short overview on the dynamical holographic QCD(DhQCD)method for hadron physics and QCD matter.The five-dimensional DhQCD model is constructed in the graviton-dilaton-scalar framework with the dilaton background field Φ and the scalar field X dual to the gluon condensate and the chiral condensate operator thus can represent the gluodynamics(linear confinement) and chiral dynamics (chiral symmetry breaking),respectively.The dilaton background field and the scalar field are a function of the 5th dimension,which plays the role of the energy scale,in this way,the DhQCD model can resemble the renormalization group from ultraviolet (UV) to infrared (IR).By solving the Einstein equation,the metric structure at IR is automatically deformed by the nonperturbative gluon condensation and chiral condensation in the vacuum.We review the results on the hadron spectra including the glueball spectra,the light/heavy meson spectra,as well as on QCD phase transitions,and thermodynamical as well as transport properties in the framework of the DhQCD model.

Keywords: holographic QCD,gauge/gravity duality,QCD matter,hadron physics

1.Introduction

Quantum chromodynamics (QCD) is the fundamental theory of strong interaction describing more than 99% of visible matter in the Universe.Though it is quite successful in the ultraviolet region when the coupling is weak[1,2],it remains an outstanding challenge to solve nonperturbative QCD physics in the infrared (IR) regime,especially the chiral symmetry breaking and color confinement related to hadron physics as well as QCD phase transitions.To tackle this problem,some important nonperturbative methods have been developed,especially lattice QCD [3–6],Dyson–Schwinger equations [7,8],and functional renormalization group equations (FRGs) [9–11].In recent decades,the anti-de Sitter/conformal field theory (AdS/CFT) correspondence or gauge/gravity duality [12–14]has been widely used in dealing with nonperturbative QCD problems in hadron physics and strongly-coupled quark matter.

It is expected that there exists a general holography principle,which maps a D-dimensional quantum field theory(QFT) to a (D+1)-dimension quantum gravity,and the gravitational description becomes classical when the QFT is strongly coupled.The extra dimension here can be treated as an emergent energy scale or renormalization group(RG)flow in the QFT [15].Therefore it is possible to construct a nonconformal five-dimensional holographic QCD model based on the gauge/gravity duality,and there have been lots of efforts both from top-down and bottom-up approaches.From top-down,the Dp-Dqsystem including the D3-D7[16]and the D4-D8system or the Witten–Sakai–Sugimoto (SS)model [17,18]have been widely explored.In the bottom-up approach,the hard-wall AdS/QCD model [19]and the softwall AdS/QCD or KKSS model [20]established the fivedimensional framework for light hadron spectra.Interesting progress was made in [21–24]to incorporate linear trajectories and chiral symmetry breaking.

The chiral symmetry breaking and the color confinement are two important nonperturbative features of QCD.From the light meson spectra,one can read the information of the chiral symmetry breaking and the linear confinement from the mass difference between the chiral partners and the linear Regge trajectory,respectively.The spontaneous chiral symmetry breaking is well understood by the dimension-3 quark condensate 〈〉 in the vacuum and the understanding of color confinement remains a challenge.The linear Regge trajectories of meson spectra suggest that color charges can form the string-like structure inside mesons thus the confinement can manifest itself by the linear potential between quark–antiquark at large distances.The dynamical holographic QCD(DhQCD) model [25–27]has been constructed by promoting the soft-wall model to a dynamical model with gluon dynamics background and the probe of matter part in the graviton-dilaton-scalar framework,where the dilaton background field Φ(z) is dual to the gluon operator and the scalar field X(z) is dual to the quark operator at the UV boundary.Evolution of both Φ(z) and X(z) along the fifth-dimension from ultraviolet (UV) to infrared (IR) resembling the renormalization group.The gluon dynamics background is solved by the coupling between the graviton and the dilaton field Φ(z)describing the gluon condensate and confinement,and the scalar field mimics chiral dynamics.The metric structure at IR is automatically deformed by the nonperturbative gluon condensation and chiral condensation in the vacuum,thus the DhQCD model can simultaneously describe both the chiral symmetry breaking and linear confinement.

Apart from the DhQCD model,the Gubser model[28–30]and the improved holographic QCD model [31–33]with the dilaton potential,the refined model [34]and Dudal model [35]with the deformed metric belong to the same graviton-dilaton system.In the graviton-dilaton system,the deformed metric,the dilaton field and the dilaton potential should be solved self-consistently from each other through the Einstein equations and the equation of motion of the dilaton field.Therefore,the three types of models,(A) with the known form of the dilaton field,(B)with the known deformed metric,and (C) with the known dilaton potential to solve the other two unknowns of the system are equivalent to describe the background at zero temperature and zero density.

In the DhQCD model,we input the dilaton field Φ(z)which is dual to the gluon condensate operator at UV.With the deformed metric by the gluon condensation,the DhQCD model can well describe the glueball spectra including the scalar glueball [25],and charge parity even and odd twogluon and three-gluon glueball spectra [36,37].Considering the backreaction of the scalar field on the background,the DhQCD model can describe the light meson spectra and pion form factor[25].It can also be extended to four flavor case to describe heavy-flavor meson spectra [38].Further studies[39–41]show that this DhQCD model can successfully describe QCD phase transition,thermodynamical properties and transport properties of QCD matter,especially the temperature dependent shear viscosity,bulk viscosity,electric conductivity as well as jet quenching parameter.

The paper is organized as following: we introduce the general graviton-dilaton-scalar framework in section 2.Then in section 3,we introduce the glueball spectra,light and heavy flavor meson spectra in the DhQCD model.In section 4.1 we introduce the thermodynamical and transport properties from the DhQCD model,and in section 4.2 we introduce how to realize chiral phase transition.Finally,a short summary is given in section 5.

2.The general graviton-dilaton-Scalar system

To apply the holographic method in QCD,one of the main tasks is to break the conformal symmetry in the original AdS/CFT correspondence.A usual way is to consider the coupling between the background gravity and the dilaton field Φ,in which the QCD relevant scales could be introduced.The 5D effective action for the graviton-dilaton coupled system could be derived from 10D supergravity[31,32,42]and it takes the following form

in which the string frame is taken.Here,gSMNis the metric in string frame,gSis the determinant of the metric,R is the Ricci scalar,Φ is the dilaton field,G5is the 5D Newton’s constant and VΦis the dilaton potential.

It is also not difficult to make a frame transformation to the Einstein framewhich is more convenient to study thermodynamical quantities.Then,the 5D action in the new frame reads

It is proposed that the dilaton field is dual to the effective degrees of freedom of gluons[43].It is also closely related to the Regge slope of the hadronic spectra [20]or the QCD running coupling constants [31,32].Such a 5D system is shown to give good description of the thermodynamics of pure gluon system[42].As for the flavor dynamics,the KKSS model,also named as soft-wall model,provides a good start point,by promoting the 4D global symmetry KKSS model takes the following form [20]

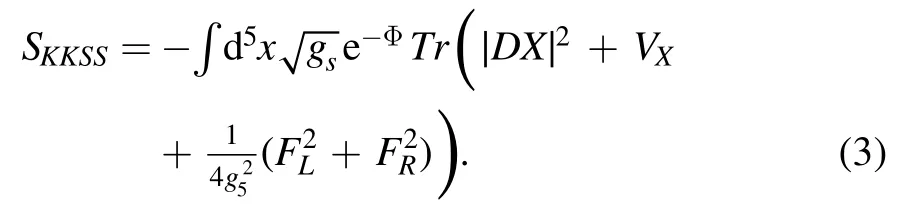
Here X is a matrix-valued scalar field Xαβ,which is dual to the operatorαqβ,with α,β flavor indexes.VXis the potential of the scalar field.The left and right-hand Gauge fields LMand RMare dual to theSU(Nf)L×SU(Nf)Rcurrents,with FLand FRtheir field strength,respectively.In such a model,one can consider a lot of interesting physics related with chiral symmetry breaking,like the quark mass effect [44,45],the multiple flavor effect [46],the isospin number density effect[47],the magnetic effect [48,49],and so on.When all the quark masses are degenerate,one usually takes the expectation value of the X filed as a diagonal form,i.e.∝χINf,withINfthe Nf×Nfidentity matrix and χ a background field dual to the chiral condensate.It is also possible to introduce the UB(1)symmetry by adding a U(1) gauge fieldFMN[50,51].

Figure 1.A sketch plot for the duality between d-dimension QFT and d+1-dimension gravity as shown in[15](Left-hand side).The RG flow from UV to IR (Right-hand side) are resembled in the dynamical holographic QCD model through the evolution of the fields in the holographic dimension.

Generally,the glue-dynamics and the flavor dynamics should be coupled together.Thus,to describe the full QCD dynamics,one has to couple the two systems,equation (1)and equation (3) together,then one reaches the full action of the holographic QCD model

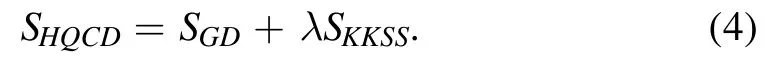
Here we explicitly write a coupling constant λ,and we assume λ tends to zero and the two systems would decouple when Nf≪Nc.In such a system,when considering the background field,one has the metric gMN,the dilaton filed Φ,the scalar field χ,thus we will call it the graviton-dilatonscalar system.When considering finite density effect,one can add the U(1) fieldFMN,and consider a general graviton-Maxwell-dilaton-scalar system.By self-consistently solving all the background out of the equations of motion,one can build the DhQCD model.

In the dynamical holographic model,the dilaton field Φ(z) and the scalar field X(z) are assumed to be dual to the gluo-dynamics and chiral dynamics,respectively.More concretely,the dilaton field Φ(z) is dual to a certain kind of gluonic operator(most likely the dimension 4 gluon condensate G2),while the scalar field X(z) is dual to the chiral condensate.The nontrivial vacuum structure of QCD indicates non-zero vacuum expectation values of those operators,which implies nontrivial boundary conditions of those background fields at the UV boundary.Then,from the equation of motion,one can dynamically solve the IR evolution of both the background field and the metric.In this way,the DhQCD could resemble the renormalization group from UV to IR with the extra dimension being interpreted as an energy scale,just as pointed out in [15]and as shown in figure 1.

The full QCD contains quark dynamics and gluodynamics and the interaction between quarks and gluons.The spontaneous chiral symmetry breaking is governed by the light flavor quarks,and the color confinement is governed by gluodynamics.The DhQCD model is constructed in the graviton-dilaton-scalar framework,where the dilaton field and scalar field play the leading role in the gluodynamics and chiral dynamics,respectively.This graviton-dilaton-scalar system can be regarded as a bottom-up ‘Dp–Dq’ system,in which the graviton-dilaton system plays the same role as the Dp brane describing the gluodynamics,while the flavor background as the ‘Dq’ brane.In principle,one should solve the whole system self-consistently.However,this is a challenging task.At the current stage,we normally use the quenched dynamical hQCD model,i.e.we do not consider the backreaction of the flavor background on the gluodynamical background,but just solve the gluodynamics background and add the flavor background as a probe.

In the following sections,we will consider the DhQCD model in different cases.

3.The glueball spectra and meson spectra

3.1.DhQCD for Glueball spectra

In this subsection,the spectra of the glueballs and oddballs are investigated.For studying glueballs/oddballs in the holographic model,there are two separate approaches,one is called “glueball fluctuation approach”,which treats scalar,vector and tensor fluctuations on the five-dimensional background metric as eigenstates of glueballs of various JPC.This approach is commonly used in top-down models,as in[52–56,32].The other approach,the one used in this work,is known as the “glueball excitation method”,which treats glueballs as Kaluza–Klein excited states by introducing the effective action of distinct glueballs on the deformed AdS5spacetime background.In this method,the total action is

where Sgis the effective action of the glueball/oddball in the string frame.This approach is widely used in bottom-up models such as [57–61],which treats glueball spectra like other meson spectra.The glueball excitation method was employed in this work to ensure that the meson and glueball spectra are treated in an equal way in the DhQCD model.

The glueballs/oddballs are excited from the pure gluon background at zero temperature and zero chemical potential,i.e.the action equation(1).The background metric is assumed to have the following form

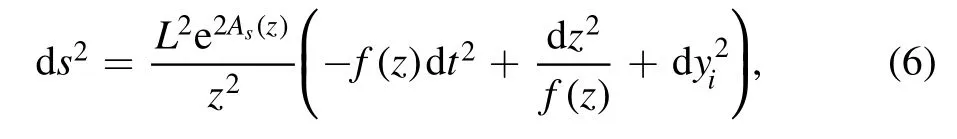
with the AdS5radius L which is set to 1 and the blackening factor f(z).Applying the Weyl transformation,the background action can be converted to the Einstein frame equation (2).The metrics in Einstein’s frame are shown as

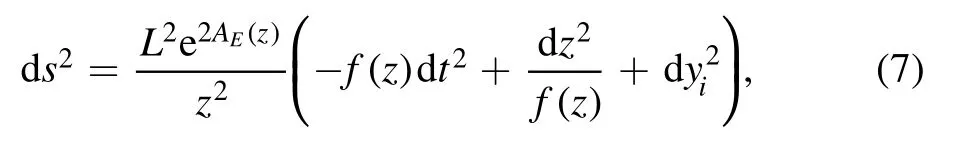
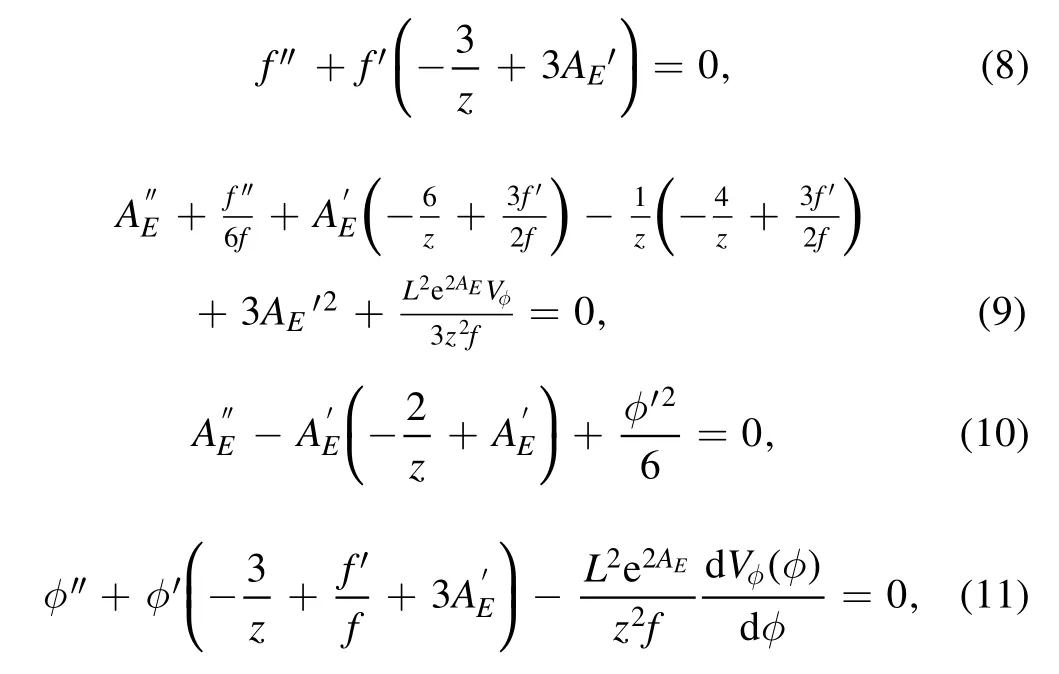
withφ=In the string frame,the effective action of the scalar,vector,and tensor glueballs/oddballs are

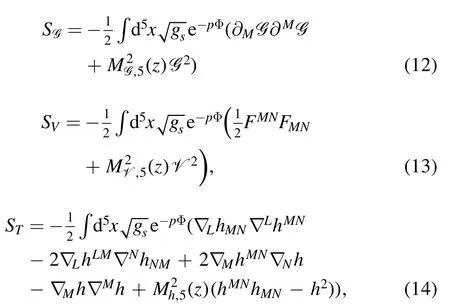
where

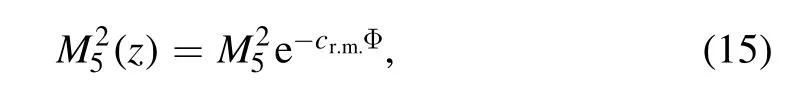
with constant cr.m.which is used to fit the glueballs spectra.The five-dimensional mass squaredM52is obtained according to the AdS/CFT dictionary,which relates the q-form field mass and the conformal dimension Δ of its dual operator[12–14]

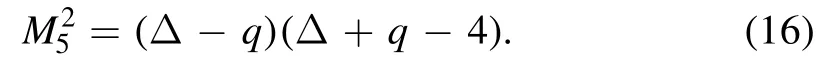
The different P-parity glueballs are distinguished by the parameter p,and p=1 for even and p=-1 for odd.The gauge invariant operators for different JPCglueballs can be obtained from [62–64,53].For the action of the tensor glueballs,the spin-2 field hMNsatisfies the following conditions

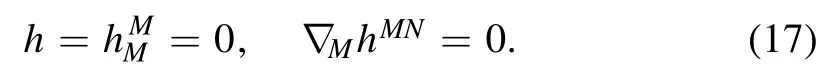
For higher spin glueballs(spin≥3),the action is shown in[20,37]and will not be shown specifically here.

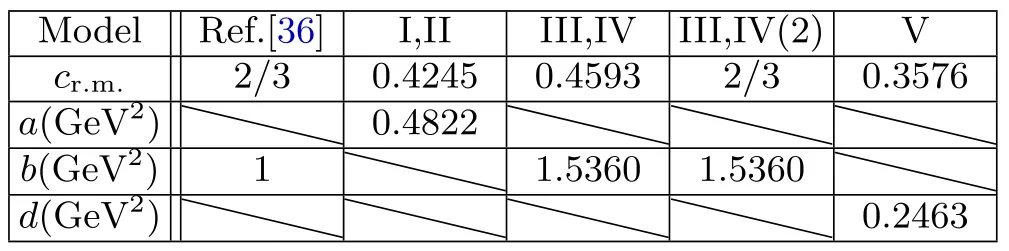
Table 1.The parameters of[36]and[37],where the Model I,II,III,IV,and V are from [37].

The equations of motion of the glueballs with different spin can be obtained from the action equations ((12)–(14)).The equations of motion of the scalar glueball are given as

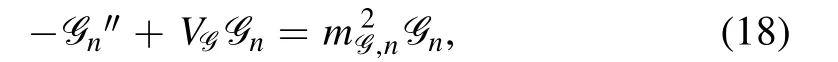
wheremG2,nis the four-dimensional momentum square of the glueball with discrete n.The potential in the Schrödinger-like equation is

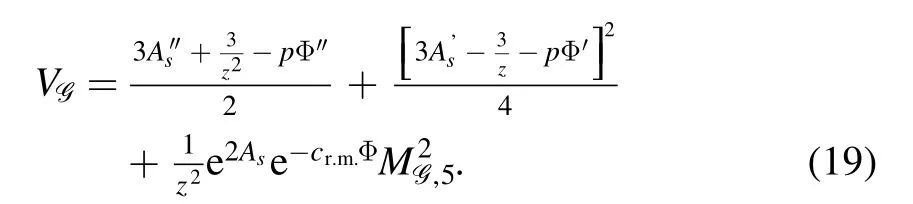
The equations of motion for the vector glueballs have the following form

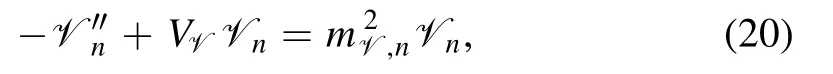
where the potential is written as

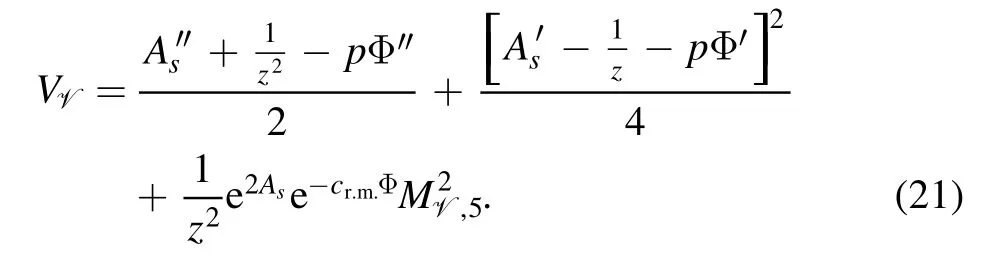
The Schrödinger-like equations for the tensor glueballs are

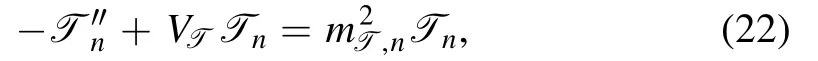
with the potential

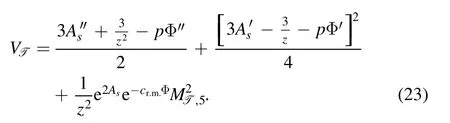
For higher spin glueballsH (spin≥3),the equations of motion have the similar form

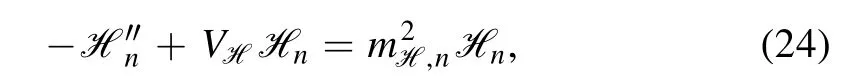
where the potential in the equation is

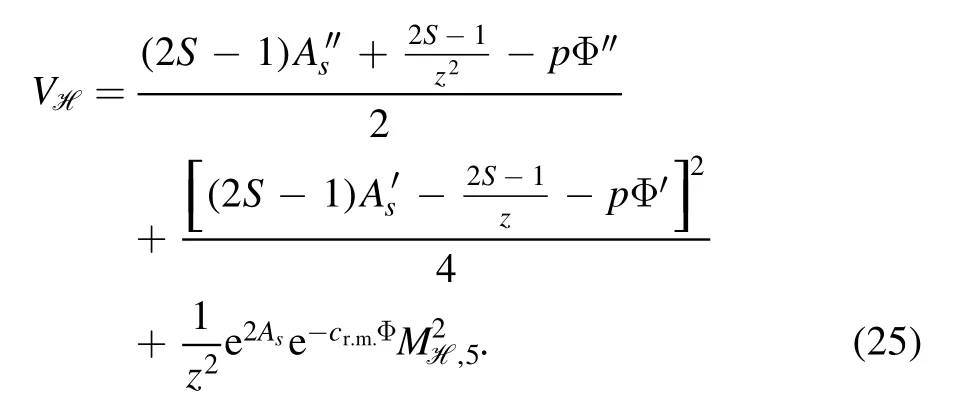
The parameters chosen for [36]and [37]are listed in table 1.By choosing cr.m.=2/3,the DhQCD model has only one free parameter b=1 GeV2,which is fixed by the Regge slope of the 0++scalar glueball spectra.Here,for solving the graviton-dilaton background,the dilaton configuration Φ=bz2is chosen.The final results of the glueball/oddball spectra are shown in figure 2,which are in good agreement with the lattice data,except for the three trigluon glueballs 0--,0+-and 2+-,which are about 1.5 GeV lighter than the lattice data.

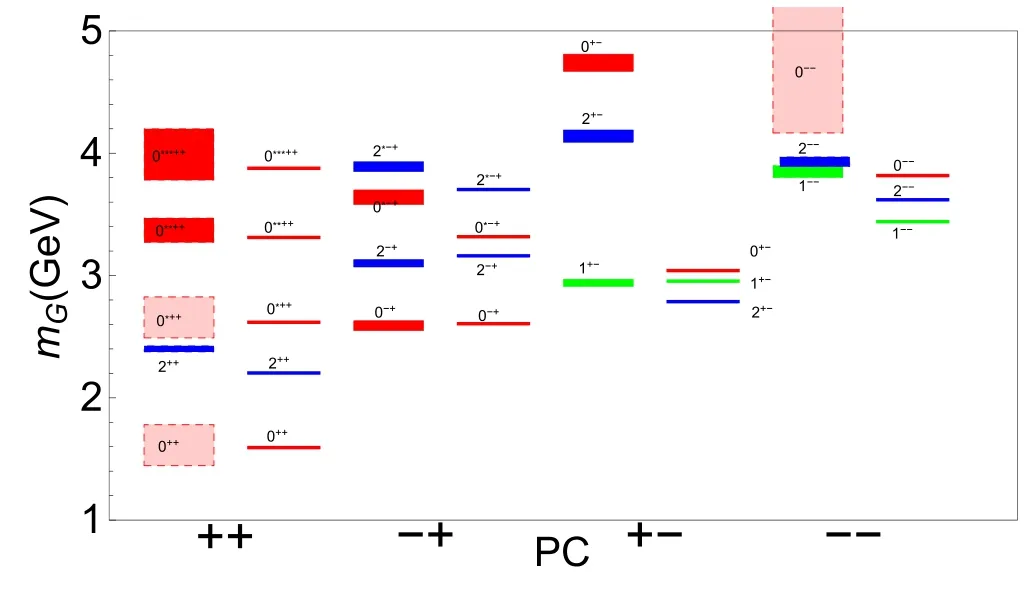
Figure 2.The glueball/oddball spectra in the DhQCD model compared with the lattice results [65–69].(The rectangles in the figure.The figure is from [36].)

Since there exist two ways to solve the gravtion-dilation system,i.e.choosing the dilaton configurationφ=and the deformed metric AE,four possible cases are considered.For ‘Model I,II’,the deformed metric AE=-az2is chosen with a=0.4822 GeV2and cr.m.=0.4245 is considered.For‘Model III,IV(1)’,the dilaton configuration φ=bz2is chosen with b=1.5360 GeV2and cr.m.=0.4593 is fixed.To compare with the results of figure 2,‘Model III,IV(2)’ sets the parameter cr.m.to 2/3 as before,where the configuration of dilaton is unchanged.Finally,a disparate dilaton configuration φ is taken into account,

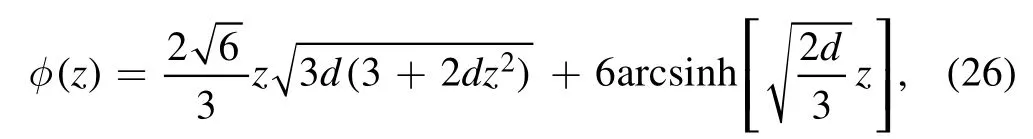
where the parameter d is chosen as 0.2463 GeV2and the parameter cr.m.is fixed as 0.3576,named as ‘Model V’.The spectra of glueball and oddball for the four cases of DhQCD model are shown in figures 3 and 4,respectively.

According to the AdS/CFT dictionary,glueballs with the same spin J and C-Parity but different P-Parity have the same five-dimensional masses,although they have different operators.To distinguish the glueball states in this case,the model introduces positive and negative dilaton couplings in the action,i.e.e-pΦ.In addition,the model includes two parameters,one in the dilaton configuration or deformed metric AEand the other in the modified five-dimensional mass squared.With these two parameters,the DhQCD model calculates the different glueball/oddball states,the results of which are compared with the lattice data and shown in figures 2,3 and 4.As can be seen from the figure,the predicted spectra of the DhQCD model for the glueball/oddball are in remarkably good agreement with the lattice results,except for the three oddball states 0+-,2+-,and 3--.It is worth mentioning the results predicted by the single pole(SP)and dipole (DP) Regge model [71],which are fitted by highenergy pp scattering: for the SP Regge model,the predicted value of the 2++glueball mass is 1.747 GeV;for the DP Regge model,the masses of the 2++glueball and the 3--oddball are 1.758 GeV and 3.001 GeV,respectively.These predictions are lower than the results of the holographic model,but still in an acceptable range.This may indicate that the 2++glueball and the 3--oddball are mixed with quark states,both of which are hybrid glueball/oddball states.

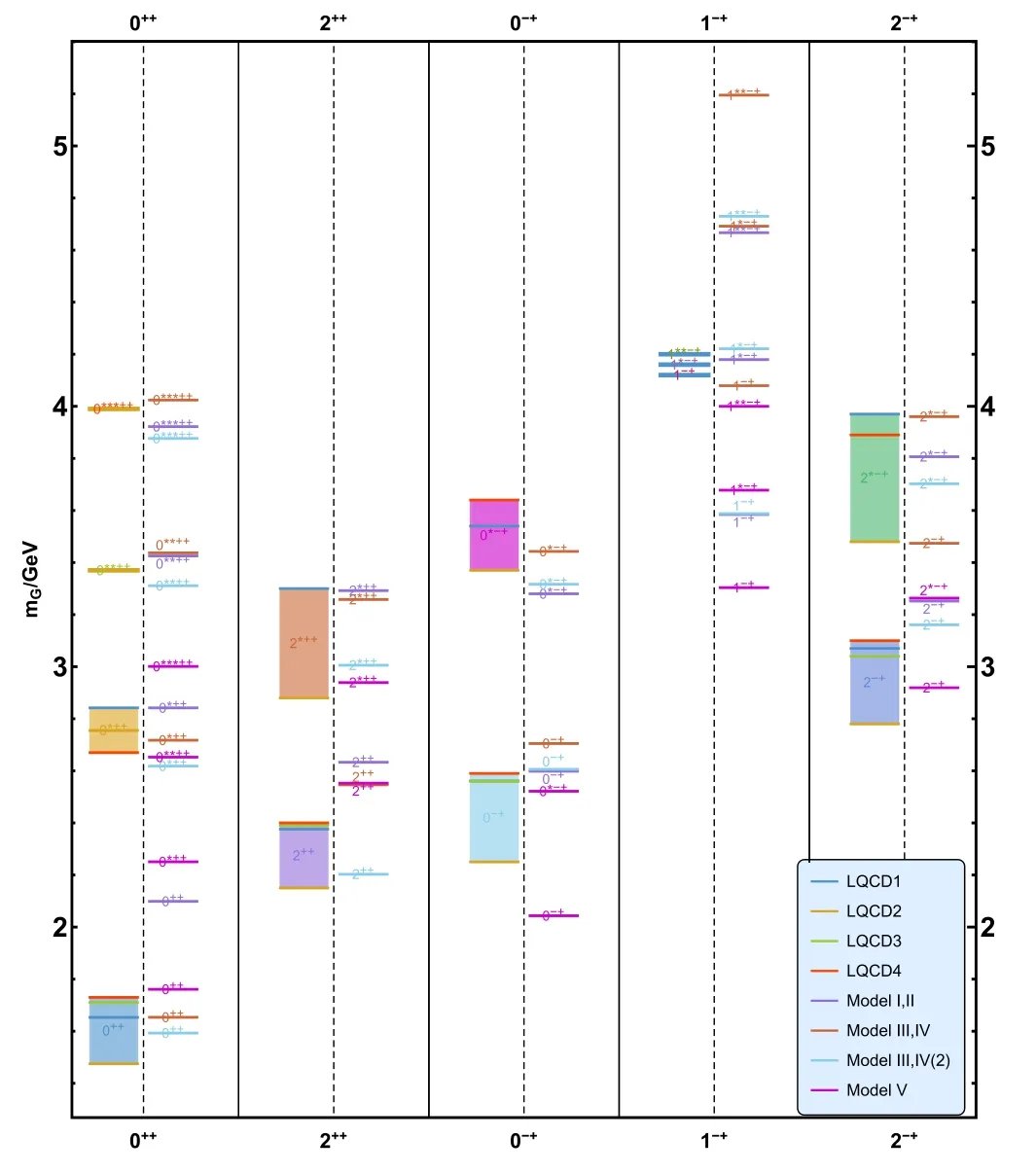
Figure 3.The spectra of distinct glueballs (C=1) in the DhQCD model and compared with lattice results.The horizontal coordinates of the graph indicate the JPC of the glueballs and the vertical coordinates indicate their mass.The rectangles on the figure are the lattice data [70,67,68,65],while the solid horizontal line denotes the DhQCD model results.The different color lines represent different models,where medium purple lines,sienna lines,sky blue lines,and magenta lines represent ‘Model I,II’,‘Model III,IV(1)’,‘Model III,IV(2)’,and ‘Model V’,respectively.The figure is from [37].

3.2.DhQCD for light flavor hadron spectra

In this section we will try to derive a self-consistent holographic model,which could describe the linear Regge behavior in the light meson spectra and the linear quark potential.We will start from the general system equation (4).Since we will focus on the vacuum,we will neglect the U(1)gauge field Fmn.Also,in the vacuum,only the metric,the dilaton field,and the expectation value of the scalar field χ is non-vanishing.Thus,for the background field,we could get the following effective action

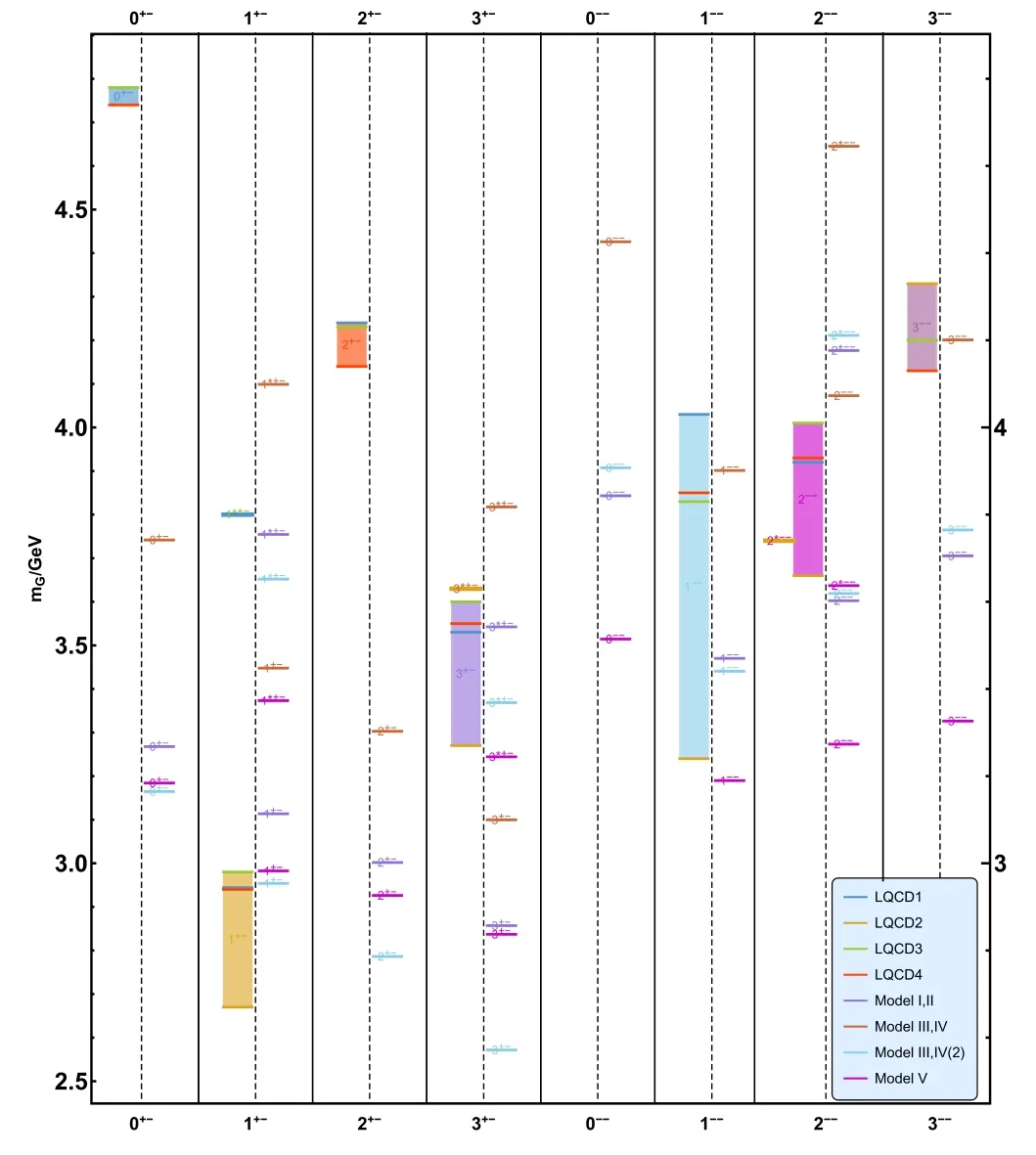
Figure 4.The spectra of distinct oddballs (C=-1) in the DhQCD model and compared with lattice results.The horizontal coordinates of the graph indicate the JPC of the oddballs and the vertical coordinates indicate their mass.The rectangles on the figure are the lattice data [70,67,68,65],while the solid horizontal line denotes the DhQCD model results.The different color lines represent different models,where medium purple lines,sienna lines,sky blue lines,and magenta lines represent ‘Model I,II’,‘Model III,IV(1)’,‘Model III,IV(2)’,and ‘Model V’,respectively.The figure is from [37].

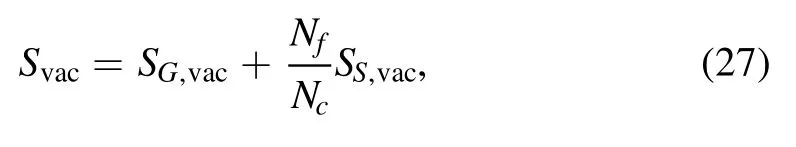
with

At zero temperature,one could take the following metric ansatz

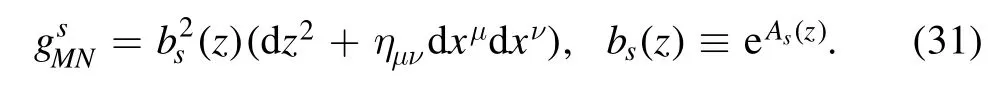
Then the equation of motion could be derived as

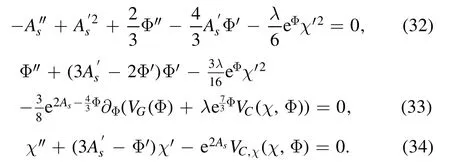
Phenomenologically,to get a consistent description of the light flavor physics,there are several constraints to be satisfied.Firstly,the IR behavior of the dilaton filed is related to the Regge slope.Secondly,to produce a linear quark potential,the derivative of the warp factor Asshould equal zero at certain zcor approaching zero when z goes to infinity.Thirdly,is responsible for the mass splits of chiral partners,thus it should not be zero at IR.Considering all these requirements,we take

with the Schrödinger-like potentials

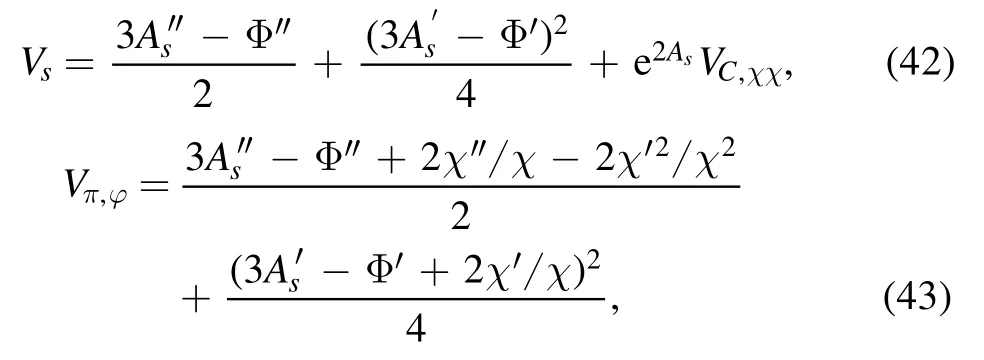
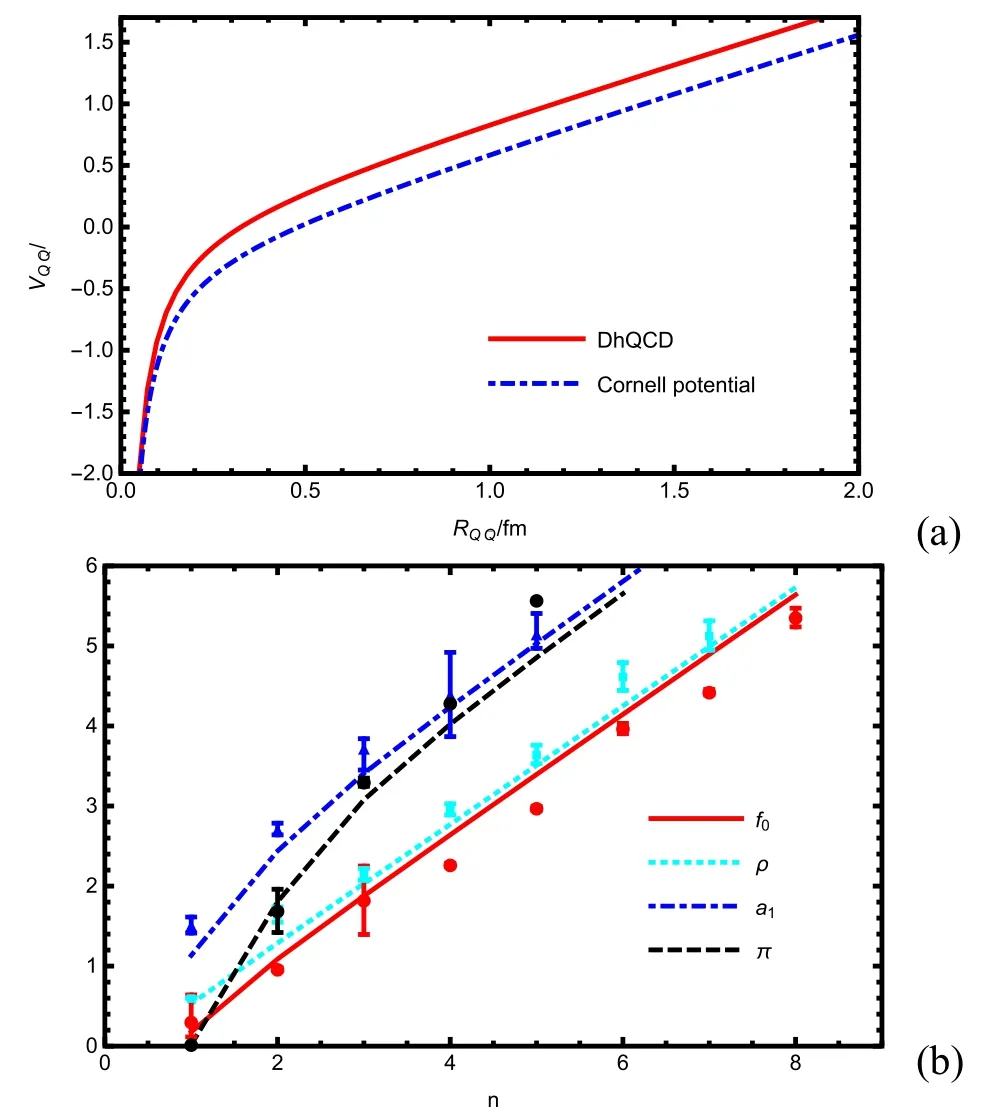
Figure 5.Results of the quark–antiquark potential and the light meson spectra from the DhQCD model,where we have taken the model IA in [26].(a) The quark–antiquark potential in the DhQCD model(red solid line)compared with the Cornell potential(blue dotdashed line).(b) The light meson spectra in the DhQCD model.

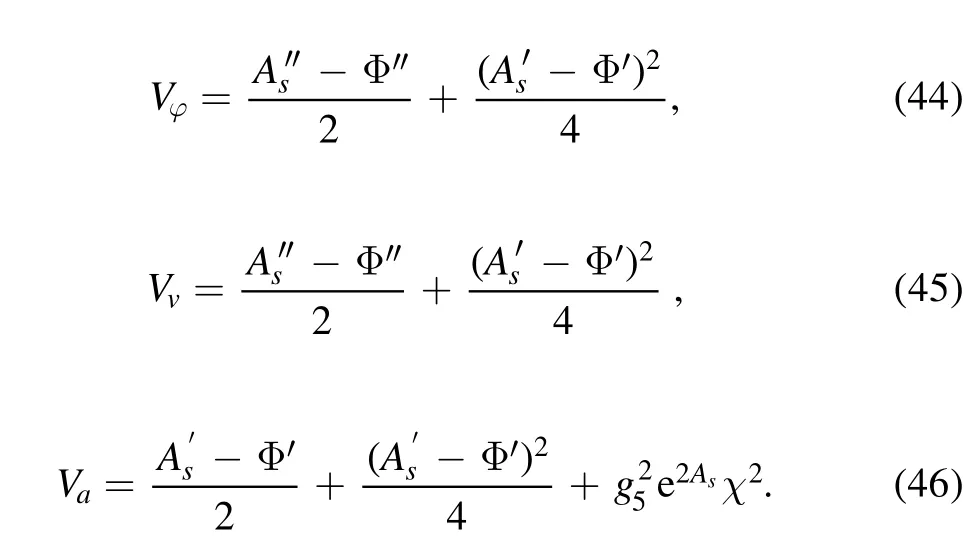
Then,the eigenvalues of those Schrödinger-like equations could be identified as the corresponding mesons’masses.The results are shown in figure 5(b).There we could see that with only four parameters the DhQCD model could match the experimental data of light mesons quite well.The linear behavior in the higher excitations is reproduced.The mass splits of the chiral partners are well described.Furthermore,by self-consistently solving the system,the linear potential and the linear spectra are realized simultaneously.

3.3.DhQCD for heavy flavor hadron spectra

In this subsection,the Nf=4 holographic QCD model describing both light and heavy mesons is introduced,which is similar to the holographic soft-wall model[20]and includes the complex scalar field X,two gauge fields LMaand RMa.The difference is that the action contains not only the dilaton field,which can describe the linear Regge behavior,but also the hard cutoff zm,which enables the splitting of the Regge slopes of light and heavy mesons.Furthermore,an additional scalar field H needs to be introduced to distinguish between vector ρ and J/ψ mesons,which are analogous to the Ψ fields[72,73]of the D4-D8 model,to characterize the large mass gap between light and heavy quarks.

Due to the difficulty of solving for the total action equation (4),the calculations in this subsection are under the probe approximation and set the background metric to AdS5.In summary,the total action describing the light and heavy mesons is

with X0=diag[vl(z),vl(z),vs(z),vc(z)].Based on the AdS/CFT correspondence,the expansion of the field at the conformal boundary yields the source and expectation values of its dual operator,and therefore,vl,s,c(z) in X0has asymptotic behavior vl,s,c(z)→Ml,s,cz+Σl,s,cz3at UV boundary.Since only the effects of heavy quarks are described,another scalar field H has H=diag[0,0,0,hc(z)].Similarly,at the UV boundary,the expansion of hctakes the form hc(z)→mcz.It should be noted that mc≠Mcwas considered in order to obtain a better mesons spectra.By expanding the action equation (47) and according to the AdS/CFT duality,the meson mass and decay constants,which come from the quadratic term of the action,and the three-and four-point coupling constants,which come from the cubic and quartic terms of the action,respectively,can be obtained.

The equation of motion for the scalar field can be written as

The analytic solutions are

with the confluent hypergeometric function U,the generalized Laguerre polynomial L and two constants C1(q) and C2(q).The equations of motion for the pseudoscalar,vector,and axial vector meson wave functions are shown below

where V,A and φ,π denote the vector,axial vector and pseudoscalar,respectively.Through the two-point function,the decay constants of the mesons are

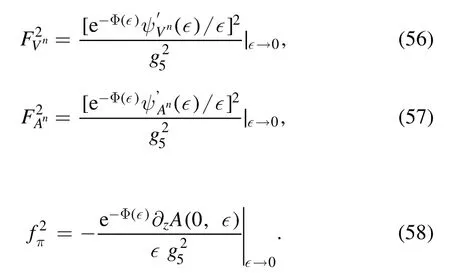
The coupling constants between the mesons can be obtained through the three-and four-point functions as

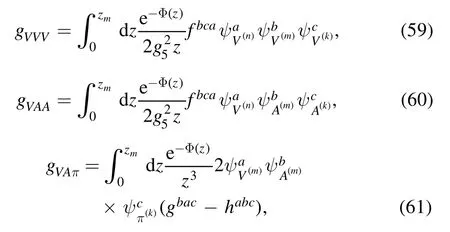
and

where ψ is the eigenwave function given by the equation of motion.Here,MAab,MVab,mVab,habc,gabc,gabcd,labcd,habcd,kabcd,and fabcdappearing in the equations of motion and coupling constants are defined as

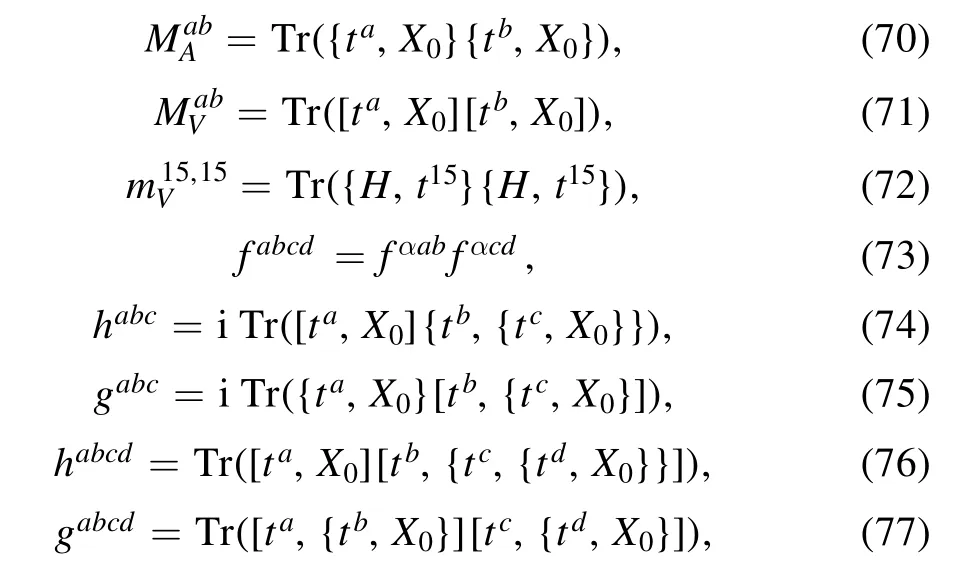
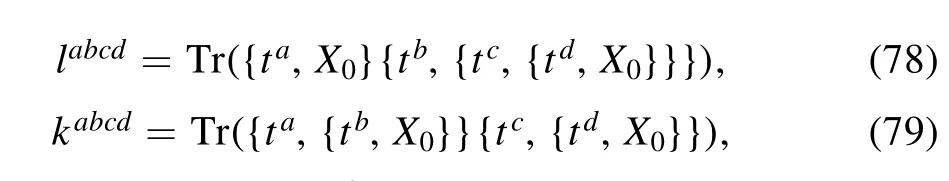
Figure 6.The mesons spectra of the holographic QCD model with Nf=2+1+1,where the dashed line represents the experimental data,selected from the PDG [74],while the solid line indicates the results of the model.The different colors are used in the figure to denote the different constituent quarks in the mesons,with red,green and blue representing ud,s and c quarks,respectively.The figures are from [38].

with structure constant fabcof SU(4) Lie algebra.

The final mesons spectra of the model are shown in figure 6,where the dashed lines denote the experimental data,chosen from the PDG [74],and the solid lines indicate the numerical results.The red,green and blue in the figure represent u,d,s and c quarks,respectively,which are used to identify the different constituent quarks of the mesons.

In the holographic QCD model describing the heavy flavors,there are six physical parameters,including the quadratic term coefficients μ of the dilaton field and the IR cutoff zm,which are used to fit the Regge slope of the light and heavy mesons,the vacuum expectation value C1(q)of the four flavor quarks,i.e.the u,d,s,and c quarks,with q=(l,s,c),and the constant D1of the auxiliary field H,which characterizes the mass difference between the light and heavy quarks.

The above six parameters are fitted by the following process.the quadratic term coefficient μ of the dilaton field is chosen to be 0.43 GeV,considering that the ground state mass of the vector meson ρ depends only significantly on it,at which point the mass of the ρ meson and the Regge slope can be fitted simultaneously.After fixing the value of μ,the vacuum expectation value C1(q) of the four flavor quarks is fitted using the masses and the Regge slope of the meson a1,K*and χc1,respectively.The last two parameters,zmand D1,which are associated with heavy mesons,are chosen based on the mass of the J/ψ meson and its Regge slope.For better numerical results,these two parameters are finally determined by the masses of the J/ψ and ψ(3770) mesons.Applying the method of expanding the field X at the conformal boundary,the parameters C1(q) can be transformed into quark masses and condensations,and the final results are Ml=140 MeV,Ms=200 MeV,Mc=1200 MeV and Σl=(1 35 MeV)3,Σs=(1 52 MeV)3,Σc=(2 76 MeV)3.Similarly,the parameter D1indicates mc=1020 MeV andσc=(2 62 MeV)3.Itwhich is not consistent with the should be noted that the QCD phenomenology suggests results of the holographic model.The problem may come from the soft-wall model itself,since the two integration constants C1and C2of the equations of motion of the scalar field are not chosen arbitrarily.As described in[26],since C2leads to nonlinear behavior of the a1meson spectra that must be set to 0,the only integration constant C1determines the quark mass and condensation,making the value of condensation proportional to the quark mass.The solution is to consider the backreaction of the scalar field and to solve the probe and the background together,i.e.to solve the Einsteindilaton-scalar system,as in [26].

In the above way,the parameters of the model are fixed and the masses of the pseudoscalar,vector and axial vector mesons and their excited states can be obtained,as shown in the solid line in figure 6.The calculations of the holographic model show that the results for the axial vector a1and K1mesons are in good agreement with the data;the results for D1and Ds1mesons are about 0.2 GeV heavier than the experimental data;the ground state and the first two excited states of χc1mesons are good,while their third excited state is about 0.2 GeV heavier than the data.It is worth noting that the results for f1mesons deviate slightly from the data because the mixing of s and u,d quarks is not considered.

For vector mesons,the excited state results for K*mesons are about 0.2 GeV lighter than the experimental data,which can be obtained from the deviation of their Regge behavior,probably because the masses of s quarks and u,d quarks are too close in the model;the ground state masses of D*mesons are about 0.3 GeV heavier than the data,while the excited states are relatively better;the first and third excited states of the ψ mesons do not match the data very well.For light vector mesons,the results are degenerate,i.e.no distinction can be made between ρ and ω mesons.In principle,the distinction can be achieved by adding additional parameters to the auxiliary H-field.As can be seen from the specific values,the results are closer to ρ mesons than to ω mesons,due to the omission of the mixing of s quarks with u,d quarks.As for the selection of ω mesons instead of φ mesons,the reason is that the equations of motion of vector mesons are closer to the pure,states.

It is notable that the mass of the experimentalDs1* (2700)state is close to that of the second excited state of the Ds1in the holographic model.Considering that the Regge slope depends only on the constituent quarks of the mesons,it is conjectured that a new excited state may exist betweenDs1*(2700)and Ds1,with a mass of about 2436 MeV predicted by the model.

From the results,it can be seen that the excited state mass of the pseudoscalar η meson is about 0.25 GeV heavier than the data,but its Regge behavior is still maintained,probably due to the missing mixing term as in the case of the ω meson;the ground state masses of the D and Dsmesons are 0.2 GeV lighter than the data;the ground state mass of ηcmesons is 0.4 GeV lighter compared to the data.It is known thatη′mesons are associated with chiral anomalies,so η mesons rather thanη′ mesons are considered in the model.For the π meson,its second,third and fourth excited states are approximately 0.15–0.3 GeV lighter than the data,and thus its Regge slope does not match.Note that the Regge slope of the π meson in the experimental data is not consistent with that of the other light mesons,so there are still difficulties in realizing this difference in the holographic model.

The holographic model not only introduces the dilaton field,but the additional IR cutoff zmand the auxiliary field H are also included,where the dilaton serves to realize the linear Regge trajectory,the IR cutoff is used to distinguish the Regge slope of the light and heavy mesons,and the H field to improve the intercept of the linear behavior of the heavy mesons.In addition,the decay constants of mesons,threepoint and four-point couplings are also calculated in the model,and the specific results can be referred to [38].

4.QCD phase transitions,thermodynamical and transport properties

4.1.Deconfinement phase transition,thermodynamical and transport properties

In this section,we will focus on the deconfinement phase transition and the thermodynamic quantities at finite temperatures from the DhQCD model.Since we would not consider baryonic density here,the U(1)gauge filed in the full DhQCD model could be neglected.Furthermore,since the centre symmetry is an exact symmetry only in the gluon system,in which the deconfinement phase transition could be well described,we will focus on the contributions from the glue-sector in this subsection.Thus,the full system would be reduced to equation (2) in the Einstein frame or equation (1)in the string frame.We will consider this scenario as a quenched DhQCD model.

From the holographic dictionary,an usual way to introduce temperature is to consider the black hole solutions and identify the Hawking temperature as the temperature of the 4D field system.Therefore,we take the metric ansatz at finite temperature in the string frame as the following form

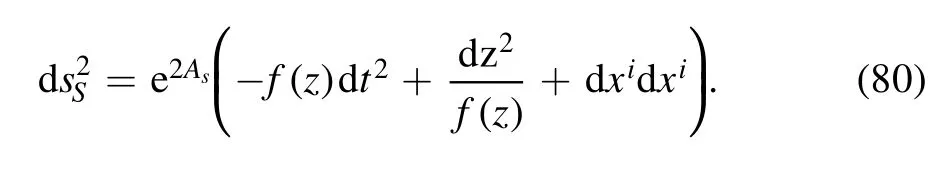
The warp factor As,the blackening factor f(z),and the dilaton field Φ(z) satisfies the following equation

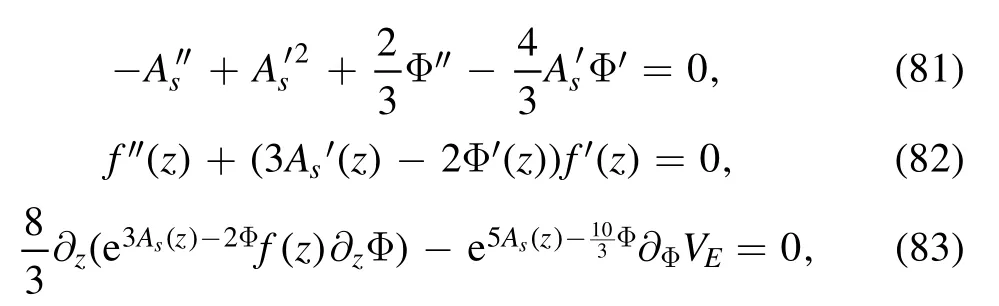
which are derived from the Einstein equations and the equation of motion for the dilaton field.Once those equations are solved out,the temperature of the black hole solution could be obtained as

with zhthe horizon where f(zh)=0.From equation (82),it is easy to get

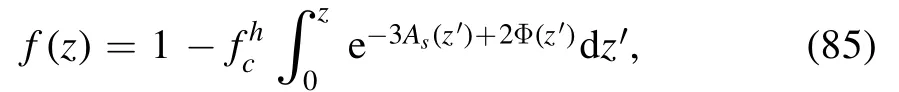
with

Therefore,one has

Meanwhile,the entropy could be identified with the Beikenstein–Hawking entropy,and its density is related to the area A of the black hole horizon through the following equation

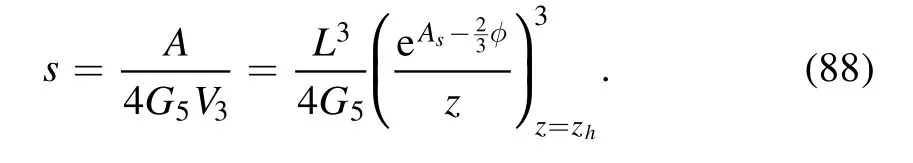
Here,V3is the volume of the system.With the expressions of the entropy density and temperature,one could derive all other thermodynamic quantities through the general thermodynamic relations.For example,one could get the pressure p,energy density ∈through the following relations

For the soft-wall model,the quadratic dilaton field is responsible for the linear Regge trajectories.So we assume that for the pure gluon system the dilaton profile should take a similar form,i.e.Φ=μGz2,with μGa mass scale.Then one can solve the equations and get an analytic solution of the metric prefactor

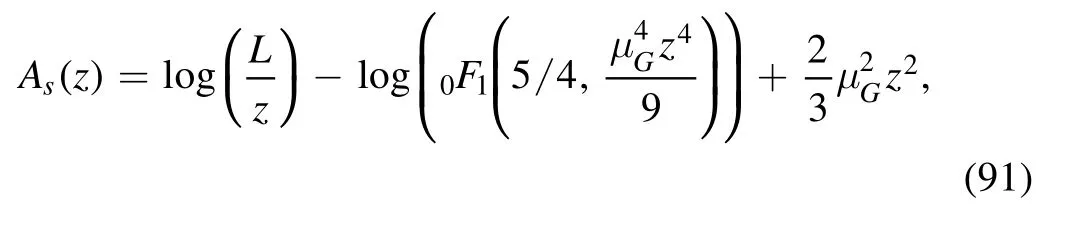
with L the AdS radius.Then one can obtain the results of temperature,entropy density,and the other thermodynamical quantities.It is found that the black hole solutions appear only above a certain temperature Tc,indicating the appearance of a phase transition.As shown in[42],the Polyakov loop,which is the order parameter of the deconfinement phase transition,becomes discontinuous near Tc.Thus,the geometric phase transition should be considered as the deconfinement phase transition,just as expected from the model building.By fitting the critical temperature Tcfor the deconfinement phase transition from the quenched lattice results,we take μG=0.75 GeV and get Tc=255 MeV.Then we can extract all other thermodynamic quantities numerically and compare the results with lattice data.

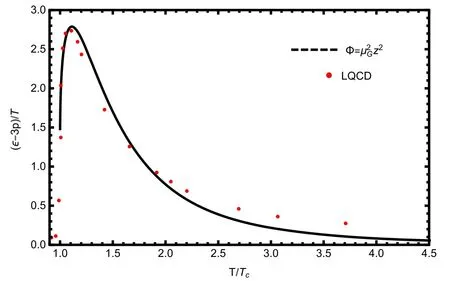
Figure 7.The trace anomaly ∈-3p from the quenched DhQCD model comparing with the SU(3) lattice data for pure gluon system from [75].We have taken μG=0.75 GeV and G5=1.25.

In figure 7,the result of the trace anomaly ∈-3p of the hot gluonic matter is shown together with the SU(3) lattice data for pure gluon system[75].From the figure,it is easy to see that the results from the quenched DhQCD model agree with the lattice data quite well.A sharp peak near Tcappears in the trace anomaly,which implies that the correct IR physics is encoded in the 5D model.

Besides the thermodynamic quantities,the transport coefficients,which characterize the response of the hot system when deviating from equilibrium states,also connect the theoretical calculations with the experiments.Therefore,after checking the effectiveness of the DhQCD model in describing the thermodynamic quantities,we would like to extend the study to the transport properties,including the jet quenching parameter,the bulk viscosity as well as the shear viscosity.

When an energetic parton pass through a hot dense medium,due to the interaction with the medium,it would lose energy to the medium.The jet quenching parameteris introduced to measure the energy loss rate.According to the dictionary proposed in [76],is related to the adjoint light like the Wilson loop

In the holographic model,the expectation value of the Wilson loop could be extracted from the on-shell string Nambu–Goto action of the dual string configuration with the 4D loop as its boundary.It is not difficult to derive the expression ofin our holographic model [39]as

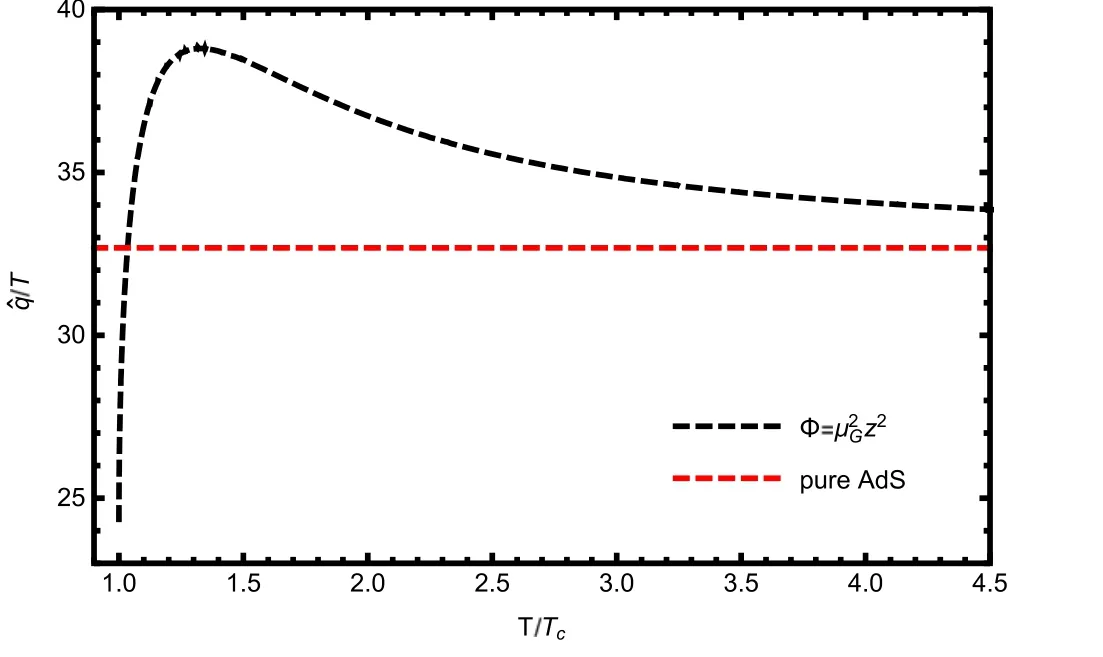
Figure 8.The T3 sclaed jet quenching parameter T3 as a function of temperature T/Tc,which is extracted from the quenched DhQCD model.We have taken μG=0.75 GeV and G5=1.25.

We insert the background solution into the above equations,and get the numerical results for the jet quenching parameter,as shown in figure 8.Different from the constant results in pure AdS background,the temperature scaled jet quenching parameterT3in the quenched DhQCD model exhibit a nontrivial behavior,especially near the critical temperature Tc.Below around T=1.1Tc,T3increases fast with temperature while it decreases smoothly above T=1.1Tc.A peak appears at around T=1.1Tc,with a height around 40.This behavior is quite similar to the peak of the trace anomaly.Both of these behaviors show the successful encoding of the novel property in the quenched DhQCD model.

The viscosity coefficients are also an important input in the hydrodynamic evolution.Theoretically,the bulk viscosity is related to the two-point function of the stress tensor through the Kubo formula

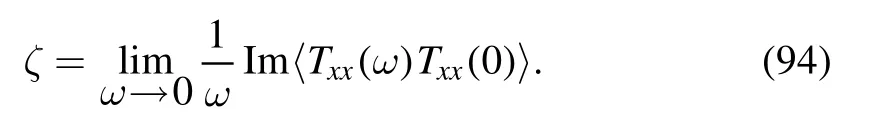
Here,Txxrepresents the diagonal components of the stress tensor.From the holographic dictionary,the two-point function could be worked out by considering the perturbation of the diagonal components of the metric δgxx≡hxx.Then one can derive the equation of motion for the metric perturbation as

Figure 9.(a) Bulk viscosity over entropy density ζ/s and (b) shear viscosity over entropy density η/s as functions of the temperature,from the quenched DhQCD model.

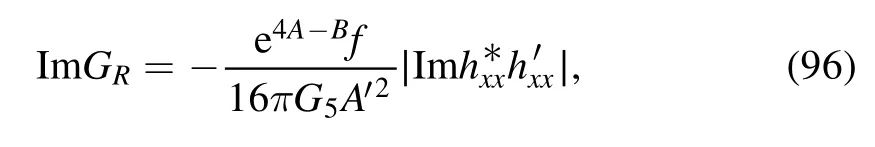
and the numerical results for ζ could be obtained.In figure 9(a),the numerical results of bulk viscosity over entropy density ζ/s are given.Again,we could see that near Tca peak appears in the ζ/s line,which is qualitatively in agreement with the lattice results in [77–79].

Similar with the bulk viscosity,the shear viscosity can also be worked out through the Kubo formula

The only difference is that in the shear case one has to consider the off-diagonal components Txy,and correspondingly the perturbation of δgxy≡hxy.Then one can derive the equation of motion for hxyand after solving it one gets the numerical results of η.Unfortunately,it is proved that for any isotropic Einstein gravity,the value of η/s would always be 1/4π,no matter how one deforms the background metric.Such a trivial constant η/s result is different from many well known systems,like water,helium,nitrogen and so on,of which η/s show a minimum near the transition temperature.To get a nontrivial behavior of η/s,following [80],we consider the higher derivative term

as a probe,where β,γ are two parameters controlling the contribution of the higher derivative term.Considering the metric perturbation in such a gravity system,one could derive η/s up to the order of O(β) [80]as

withc0=Then we takeβ=0.01,γ=and show the numerical results in figure 9(b).Interestingly,we see that a valley appear at T=1.1Tc.Therefore,from the holographic study,it indicates that the phase transition has nontrivial effect on the transport coefficients.For more details about this part,please refer to [39,40].

4.2.Chiral phase transition

In the previous sections,the DhQCD model is shown to give a good description of glue-dynamics and thermodynamics.The deconfinement phase transition could be described as well.In this subsection,we will transfer to the flavor dynamics and focus on the chiral phase transition in this model.Since solving the DhQCD model with finite temperature,density is not an easy task,we will treat the flavor part as a probe.Within such a scenario,the dynamical part of the action would reduce to the soft-wall model action

Here,since only the scalar part is relevant for chiral phase transition,we neglect the other parts in the full action.As mentioned above,there is aSU(Nf)L×SU(Nf)Rgauge symmetry in this action.But if the scalar field X has a nonzero value X0,this symmetry would be broken toSU(Nf)V.That is the holographic realization of the 4D spontaneously breaking of chiral symmetry.Considering the symmetry of the background,one haswithINfthe Nf×Nfidentity matrix.Since chiral condensate is homogeneous at finite temperature,χ(z) depends on the holographic coordinate z only.Inserting those conditions into the action,one reaches the effective form of the action

We take the following simple scalar potential

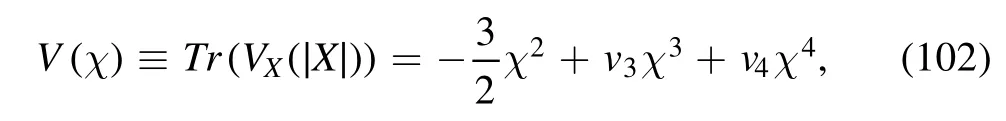
where we have taken the mass term as-3X+X,the cubic term comes from the determinant of X and the quartic term v4χ4is introduced to get non-zero condensate at low temperature.Different from the 4D field theory,such a potential is insufficient to get non-zero condensate.It is shown that the derivative of the dilaton profile Φ′ (z)should take negative values in the scale of chiral dynamics.Combining with the requirement of the linear confinement in the confinement scale,we take the following form for the dilaton field

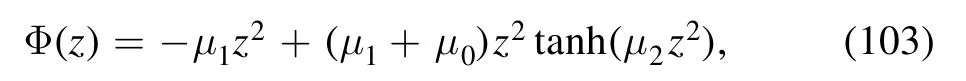
which is the interpolation of the requirement in the scales of chiral and confinement dynamics.Though there are other kinds of modification,but interestingly all of them requires two scales to incoorperate the two dynamics,which is in agreement with the instanton liquid model studied in [81].To get the reasonable values of the Regge slope,the vacuum condensate and the transition temperature,we take the parameters asμ0=(0.43) (G eV)2⋍0.18 GeV2,μ1=(0.83 GeV)2⋍0.69 GeV2andμ2=(0.176 GeV)2⋍ 0.03 GeV2,v3=0,v4=8 for two flavor case.As for three flavor case,to consider the instanton effect,we replace the value of v3with v3=-3.If all the quark masses are degenerate,the equation of motion could be derived as

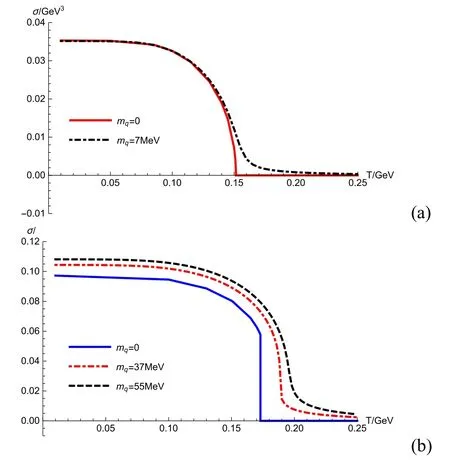
Figure 10.The chiral condensate σ as a function of the temperature T in 2-flavor case (a) and 3-flavor case (b),respectively.

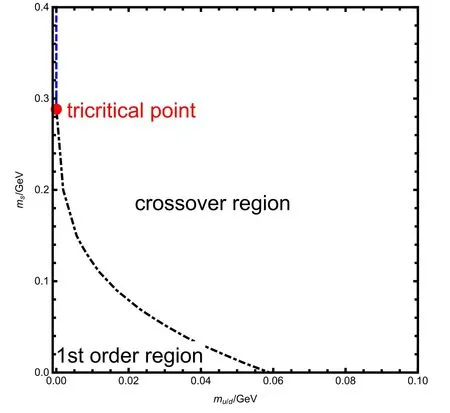
Figure 11.The phase diagram of chiral phase transition in the quark mass plane.

The UV expansion of the solution could be obtained aswith mqthe quark mass,σ the chiral condensate,andζ=[82].By requiring the regularity of the solution at the horizon,one can solve σ as a function of mqand T.The results are given in figure 10(a) for two flavor with v3=0 and in figure 10(b) for three flavor with v3=-3.

From the figure,one could see that: in the chiral limit of two flavor case,the phase transition is a second order transition,and any finite quark mass would drive the transition to a crossover one;in the chiral limit of three flavor case,the phase transition turns to be a first order one,and only sufficient large quark mass (＞37 MeV) could drive it to a crossover transition.

The above study could be extended to ‘2+1’ flavors case,i.e.mu=md≠ms.Then the diagonal part of the scalar field X becomes different,we have χu=χd≡χl≠χs.Then we have to solve the coupled equations

Similarly,the quark masses and condensates could be read from the UV expansion as χl=mlζz+...+σl/ζz3+...,χs=msζz+...+σs/ζz3+...,with ml=mu=mdthe light quark masses,msthe strange quark mass,andσl=〈〉=Then one can solve the condensates from the above equations and get the mass dependence behavior of the phase transition.The results are summarized in figure 11.It is shown that the whole mass plane is divided into two parts,which are separated by a critical line (the blue and red segments in figure 11).In the corner near the three flavor chiral limit,the chiral phase transition is a first order phase transition,while it is a continuous crossover in the other side of the critical line.It should also be noted that there is a tricritical point in the critical line,which divides the critical line into two parts with different critical exponents,as shown in the figure.Qualitatively,the results agrees quite well with the‘Columbia plot’ [83,84].For more details,please refer to[41,44,46,45].

4.3.Quarkoynic phase at finite baryon density

Now we consider the quenched DhQCD model in[25,26,40]at finite chemical potential by introducing an extra U(1) field in the Einstein–dilaton–Maxwell framework,and the action in the string frame takes the form of [50]:

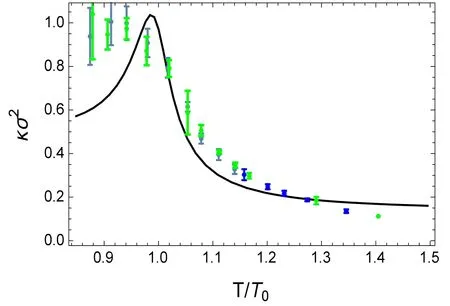
Figure 12.The kurtosis of baryon number fluctuations кσ2 as functions of the normalized temperature T/T0 with T0=217 MeV the pseudo critical temperature at zero chemical potential μ=0.The black line is for the case of h(Φ)=7/10,which is in agreement with lattice results in [88].The figure is from [50].

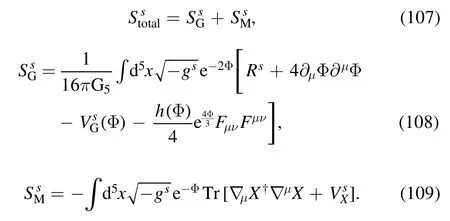
Here Stotal,SGand SMare the full 5D action,the 5D action for the dilaton background describing gluodynamics,and the 5D action for the matter sector describing chiral dynamics,respectively.The superscript s represents the string frame,G5is the 5D Newton constant,gsis the determinant of metric gμν,Φ is the dilaton field,and X is the bulk scalar field which corresponds tocondensate of QCD.VGand VXrepresent the dilaton potential and the bulk scalar potential,respectively.The leading term in VXis the 5D-mass termm52XX†,and the 5D mass square can be determined asm52=-3from the AdS/CFT dictionarym52=(Δ-p) (Δ+p-4)by taking Δ=3,p=0 [14,85].Fμνis the strength tensor of gauge field dual to the baryon number current,and Fμν≠0 corresponds to the finite baryon number chemical potential case of the system.We take the dilaton field in the form of

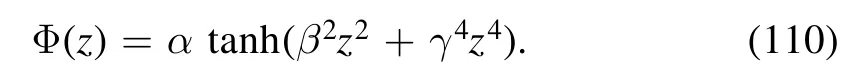
By fitting the equation of state of lattice QCD for Nf=2[86],the parameters of the dilaton field can be fixed to α=1.8,β=0.4 GeV,γ=0.42 GeV as in [87,50].h(Φ) is a gauge kinetic function constraining the μ dependence of the system and can be fixed by fitting the lattice data on the kurtosis of baryon number fluctuations,with the baryon number susceptibilitiesкσ2=C4B/C2B,where the varianceσ2=C2Band the kurtosisк=C4B/(σ2)2,and the cumulants of baryon number distributions are given byCnB=VT3χBn.

Figure 13.The (T,μ) phase diagram for chiral and deconfinement phase transitions with the blue dashed line and the black line for deconfinement phase transition and the chiral phase transition,respectively.A chiral symmetric but deconfined phase showing up in the region of large chemical potential.The figure is from [50].

The baryon number susceptibilities are defined as:

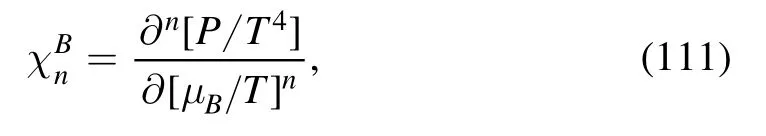
with P,V the pressure and volume of the system,and μB=3μqthe baryon number chemical potential.

Figure 12 shows the kurtosis кσ2as a function of the normalized temperature T/T0with T0=217 MeV,which is comparable with the lattice result [88].It is found that whenh(Φ)=,the result of kurtosis in the quenched DhQCD model is in good agreement with lattice results.

As shown in [50],We can solve out chiral condensate σ as well as the Polyakov loop as functions of T and μ.Then we can extract the critical temperatures and chemical potentials for chiral phase transition and deconfinement phase transition,respectively.The result is shown in figure 13,with the blue dashed line for the deconfinement phase transition and the black line for the chiral phase transition,respectively.It is seen that the deconfinement phase transition is always a crossover and it shows weak dependence on the quark chemical potential,while the chiral phase transition is a crossover at low chemical potential and turns to a first order phase transition at high chemical potential,with a CEP at (TE,μE)=(0.20,0.21)GeV on the chiral phase transition line.It can be observed that the chiral phase transition line has much stronger dependence on the quark chemical potential than the deconfinement phase transition,thus one can observe a quarkyonic phase [89],i.e.the chiral symmetric but deconfined phase showing up in the region of large chemical potential.This phase diagram is similar to that obtained in the PNJL model as shown in [90]and [91,92].

It is noticed that based on Gubser’s model[29,30,93,94],Cai et al [95]fitted lattice results at zero chemical potential much better and obtained the critical end point at(TE,μEB)=(0.105,0.558) GeV,which is in agreement with that in PNJL model in [92]and FRG [96].The equation of state at finite baryon density determines the massradius relation of compact star,which is also an interesting topic in the framework of holographic QCD model,see,for example [97].The investigation of DhQCD model at finite baryon density related to the CEP as well as the neutron star is in progress.

5.Discussion and summary

We have reported our studies on hadron physics and QCD matter in the framework of DhQCD model,which is constructed in the graviton-dilaton-scalar framework,where the dilaton background field and scalar field are dual to the gluon condensate and the chiral condensate operator thus can represent the gluodynamics (linear confinement) and chiral dynamics (chiral symmetry breaking),respectively.The dilaton background field and the scalar field are a function of the 5th dimension,which plays the role the energy scale,in this way,the DhQCD model can resemble the renormalization group from ultraviolet (UV) to infrared (IR).By solving the Einstein equation,the metric structure at IR is automatically deformed by the nonperturbative gluon condensation and chiral condensation in the vacuum.

It is seen that the pure gluon system can be well described by the graviton-dilaton system with a quadratic dilaton field Φ(z)=μz2,the deformed metric can be analytically solved.With this deformed metric,the glueball/oddball spectra are in good agreement with lattice result,and the thermodynamical properties of this pure gluon system including the energy density,the pressure density and the trace anomaly agree with lattice data well,and the temperature dependent transport coefficients including the shear viscosty,bulk viscosity and jet quenching parameter carry the information of the phase transition,i.e.the ratio of the jet quenching parameter over cubic temperature3,the ratio of the bulk viscosity over the entropy density show a peak around the critical temperature Tc,and the ratio of the shear viscosity over the entropy density shows a valley around the critical temperature Tc,at which the scaled trace anomaly(∈-3p)/T4also shows a peak.

Then we add the flavor part as a probe on the pure gluon system,the full DhQCD,i.e.the deformed metric can be selfconsistently solved including both the gluon condensate and chiral condensate.On this deformed metric we can solve the light-flavor meson spectra,which is in agreement with experimental data.The flavor part itself is also extended to four flavor case,and the obtained heavy meson spectra also agree well with experimental data.Furthermore,the chiral phase transition is successfully realized in the framework of holographic QCD framework.

In summary,our DhQCD model can describe hadron physics,QCD phase transition,thermodynamical properties and transport properties of QCD matter quite successfully.In this sense,we can use this DhQCD model as an effective method for nonperturbative QCD.

Acknowledgments

This work is supported in part by the National Natural Science Foundation of China (NSFC) Grant Nos.11 725 523,11 735 007,11 805 084 and supported by the Strategic Priority Research Program of Chinese Academy of Sciences under Grant Nos.XDB34030000 and XDPB15,the start-up funding from University of Chinese Academy of Sciences(UCAS),the Fundamental Research Funds for the Central Universities,the China Postdoctoral Science Foundation under Grant No.2021M703169,and Guangdong Pearl River Talents Plan under Grant No.2017GC010480.

ORCID iDs