风电场穿透功率风险下基于改进NSGA-2的动态经济调度方法
李德英,陈希祥,陈 钢,易 涛
(湖南信息学院 电子科学与工程学院,湖南 长沙 410151)
0 引言
风电穿透功率极限是指电力系统在满足各种运行约束条件下,所接受的风电最大装机容量占系统负荷的比例[1],[2]。风电穿透功率极限影响风电并网规划和电网安全稳定运行[3],[4]。风电具有很强的不确定性,在经济性调度时,如果只考虑系统正、负旋转备用,则无法实现最优调度。
近年来,确定风电场的穿透功率[5],[6]和计及穿透功率风险下实现最优化的调度,成为重要的研究课题。在风电经济性调度研究方面,文献[7]~[10]为应对风能预测误差的影响,构建了正、负旋转备用约束模型,并以发电成本最优作为经济调度模型的目标函数。这些均为单一优化目标,且目标函数中没有考虑阀点效应成本,误差较大。文献[11]构建了以发电成本和污染排放量最小的静态多目标经济调度模型,并以系统正、负旋转备用为约束。模型没有考虑阀点效应成本,且静态调度不能正确反应风能波动性和间歇性的特点,不能实时解决调度问题。文献[12],[13]构建了含阀点效应成本的多目标动态经济调度模型,采用多种智能算法组成的混合算法对调度模型进行求解,但计算程序复杂,在工程实际中受到一定的限制。文献[14]利用改进的量子遗传算法,对含风电场的多目标动态经济调度模型进行求解。但模型未考虑负旋转备用,仅考虑了正旋转备用,不符合实际运行状态。在风电穿透功率极限研究方面,文献[15],[16]考虑了风速相关性和暂态稳定约束条件,将风电接入容量最大作为优化目标,求解风电穿透功率极限。文献[17]综合考虑了电力系统暂态稳定性和频率安全稳定约束,通过分析风速和系统保持暂态稳定的概率特性来求解电网的风电穿透功率极限,该方法是在风电场不具备惯性响应和一次调频响应能力的前提下探讨的。文献[18],[19]考虑频率约束,采用动态仿真法求解风电穿透功率极限。
目前,对含风电场的经济调度模型研究均集中在利用正、负旋转备用来减少风能不确定性的影响,以及风电穿透功率极限的计算,而对风能穿透功率风险带给经济调度的影响研究较少。本文构建了以含阀点效应的发电成本和废气排放最小为目标函数,既考虑正、负旋转备用约束,又加入系统安全水平约束应对风能穿透功率风险的动态经济调度模型。最后,通过仿真算例验证了风能穿透功率对经济调度的影响和改进算法的可行性。
1 风能预测和穿透功率确定模型
1.1 风能预测模型
风能的不确定性主要源于风速的间歇性和随机性[2]。选择Weibull分布描述风速的随机变化规律 为[20],[21]

式中:v为风速;k为形状参数;c为尺度参数。
风电机组的输出功率PWT与风速v的关系为 [2],[12]
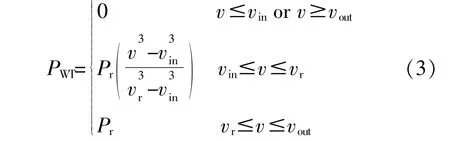
式 中:Pr为 风 机 额 定 功 率;vout,vin,vr分 别 为 切 出 风速、切入风速和额定风速。
1.2 风能穿透功率确定模型
风能穿透功率极限是影响电力经济调度的关键参数,但由于涉及的影响因素较多,至今还不能确定最佳的风能渗透量[5]。本文利用系统安全约束确定风能的渗透范围,当实际风能在安全允许范围内,全额上网;反之,则最大允许渗透值为上网 值,可 以 利 用 模 糊 隶 属 函 数 表 示[22],[23],即:

式中:W为风能的渗透功率;Wmax,Wmin分别为风能渗透的最大、最小值,由负荷预测值决定。
考虑到调度者对风能调度态度具有模糊性,采用二次模糊隶属函数表达其影响,表达式为式 中:aw,bw和cw为 函 数 系 数。

在 同 一 安 全 水 平 系 数 下,w1,w2,w3分 别 表 示调度者情绪悲观、中立和乐观的时候允许的风能渗透值[12],如图1所示。

图1 调度者不同态度的风能渗透Fig.1 The wind power penetration under the different attitudes of the dispatcher
2 计及风能穿透功率风险的动态经济调度模型
2.1 目标函数
计及风能穿透功率风险的动态经济调度是在满足系统功率平衡和运行约束的前提下,根据系统安全水平约束确定风能的渗透量和常规机组的出力,从而使系统的发电成本和废气排放量达到最优。此外,在发电成本中应考虑常规机组的阀点效应成本,否则误差较大,而风能预测误差带来的备用成本相对较小[3],暂不考虑。
①发电成本
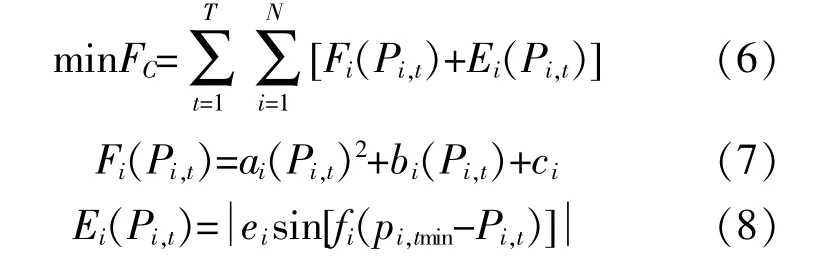
式中:FC为调度周期各个时段的发电总成本;N为常 规 机 组 数;T为 调 度 周 期;Fi(Pi,t)为 发 电 机 组i在t时 段 的 发 电 成 本[12];Ei(Pi,t)为 常 规 机 组 阀 点 效应 产 生 的 能 耗 成 本[12];ai,bi和ci分 别 为 燃 料 费 用系 数;Pi,t为 发 电 机 组i在t时 段 的 输 出 功 率;pi,tmin为组发电机组i在t时段的出力下限;ei,fi为阀点效应系数。
②废气排放量
燃煤机组中环境污染、排放量与发电功率之间表达式为[24]
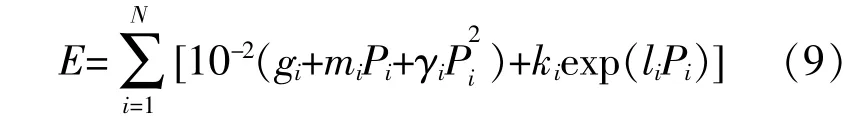
式 中:E为 污 染 气 体 排 放 量;gi,mi,γi,ki和li为 燃煤机组的污染气体排放量系数。
综上可得,本文研究的多目标函数为

式中:a1,a2分别为成本和排放量系数,且a1+a2=1。
2.2 约束条件
①功率平衡约束
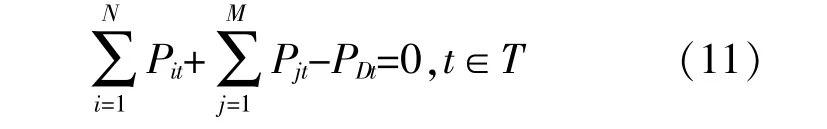
式中:Pit为发电机组i在t时段的发电量;M为系统中风电机组数量;Pjt为第j组风机在t时段输出功率;PDt为在t时段的预测负荷。
②机组出力约束

③发电机爬坡率约束
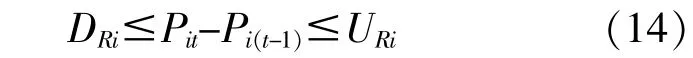
式中:DRi,URi分别为常规机组在t时段的有功出力下降和上升速率。
④系统的正、负旋转备用约束[12]

式中:USRt,DSRt分别为系统在t时段的正、负旋转备用要求,为系统总负荷的5%。
⑤系统安全约束

式中:r为系统安全约束下限。
3 NSGA-2 算法
NSGA-2算法在求解含等式约束问题时,通常利用概率的形式将等式约束转换成不等式约束[25]。为提高NSGA-2算法的求解精度,会将合适罚函数项添加到目标函数中,但其惩罚因子的选择具有随机性,如果选择不当,将使算法收敛性变差[7]。NSGA-2算法中的精英保留策略减少了种群的多样性,使最优解集易陷入局部解[26],[27]。
3.1 种群调整
传统NSGA-2算法难以快速求解含等式约束的问题。文献[7]对不满足等式约束的种群个体进行优化,其原理如下。
变量可松弛度是指非可行解中种群个体值与机组发电约束上、下限值的差值,取值大于零,其表达式为
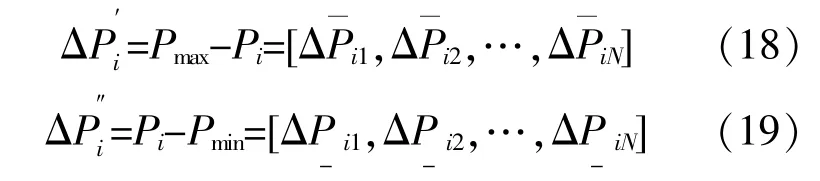
越限值是指当前非可行解违反等式约束的程度[7],其 表 达 式 为

当 ΔPi>0时,即电网计划出力大于负荷预测和网损值,采用常规机组出力下调策略[7],即:
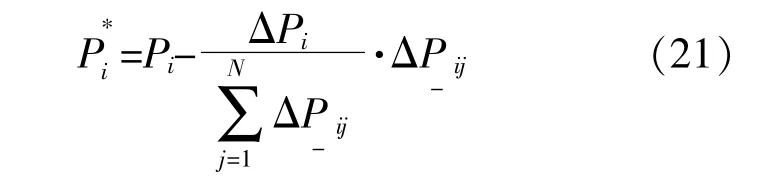
同理,当 ΔPi<0时,即电网计划出力小于负荷预测和网损值,采用常规机组出力上调策略[7],即:

3.2 精英算子改进
基于NSGA-2中精英保留算子的不足,改进后 算 子 表 达 式 为[26],[27]

式中:Nj,N1分别为非支配排序j等级中需要保留的个体数目和种群大小;k为最大等级。
采用该算式进行改进之后,解的多样性明显增加,但却存在Nj>的情况,为非支配排序j等级中的实际个体数目,因此,存在最优解集小于N的情况。文献[28]在此基础上,增添一变量来容纳两者差值,并将这差值累计给下一等级,直至完全取到N个个体,但加大了计算难度。因此,本文提出的改进算子为

图2为改进算子下不同等级个体选取概率。

图2 不同等级选取概率Fig.2 The selection probability of different levels
根 据 试 错 法,在 式(24)中 选 取r=0.75,k=10时,NSGA-2中精英保留算子优化效果最佳。通过对算式的改进,保证了在每个等级中种群个体的选取数目均>1/2,这也保证了最优种群中个体的数目为N,避免了最优种群个体数目大于实际最优种群个体数目的情况。同时,个体被选择的概率随着种群个体等级的增加而减小,这保证了精英个体被继承的概率加大,进而保证了最终种群的最优性。
3.3 经济调度流程
运用本文改进的NSGA-2算法,对计及风电场穿透功率风险的动态经济进行调度,流程如图3所示。Gmax为最大迭代次数。

图3 算法流程图Fig.3 Flowchart of the algorithm
4 算例分析
为验证风能穿透功率对系统动态经济调度的影响和本文改进NSGA-2算法的可行性,以IEEE 39系统3时段(时段1,2和3分别表示低风速、中风速和高风速时段)调度周期(每时段1h)系统为例进行仿真。常规机组的燃料成本系数、出力限制见文献[13],风机参数见文献[2]。
对文献[2]中参数进行修改,得到了常规火电机组爬坡率,如表1所示。具体的污染物排放系数与文献[29]相同,如表2所示。假设时段周期内负荷 为650MW,种 群 参 数N为20,Gmax为200;安 全风险中的Wmax,Wmin参数分别为预测负荷的30%,20%[23]。

表1 常规机组的爬坡率Table1 Ramp rate data of conventional generator

表2 机组污染物排放系数Table2 Pollutant discharge coefficient
对计及风能穿透功率风险的经济调度模型进行对比,取安全系数r=0.9,则风能的渗透范围为0~136.5MW,其 模 型 最 优 结 果 如 表3所 示。(/后 为未计及风能穿透功率风险数据,下同)。表4为不同情况下风能渗透量。表5为时段3最优情况下常规机组计划出力分配结果。图4为时段3计及风能穿透功率风险的最优解集。
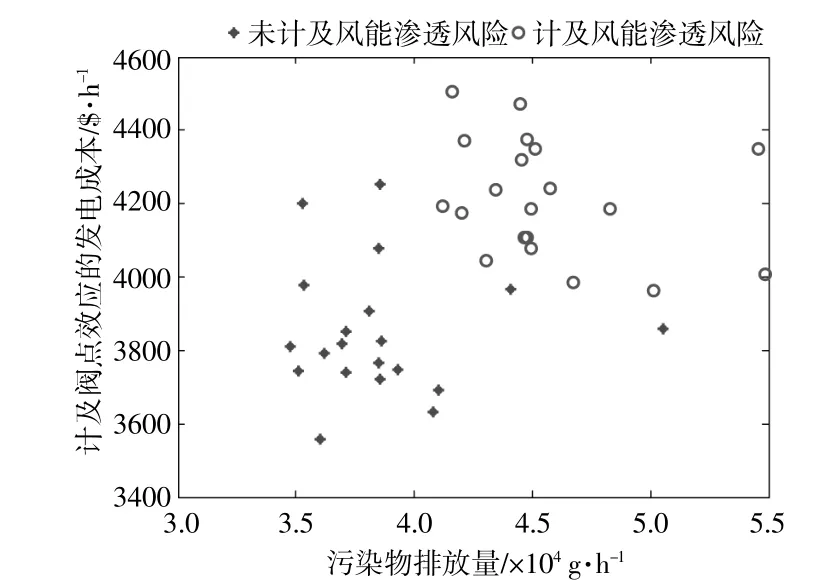
图4 考虑安全风险的最优解集分布Fig.4 The optimal solution set is consider security risks
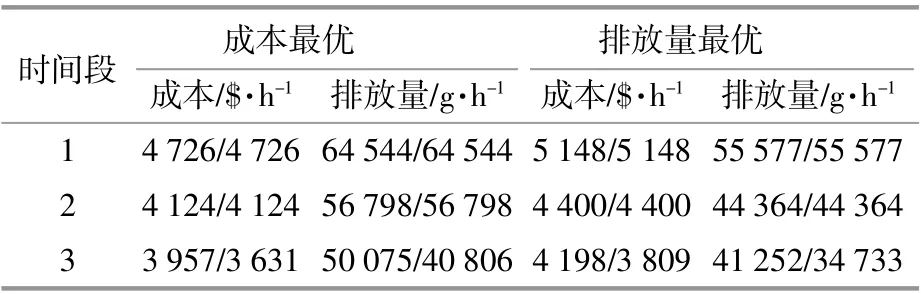
表3 不同时段成本最优值Table3 The cost optimal value under different times

表4 不同时段风能渗透值Table4 The wind power penetration value in the different times MW
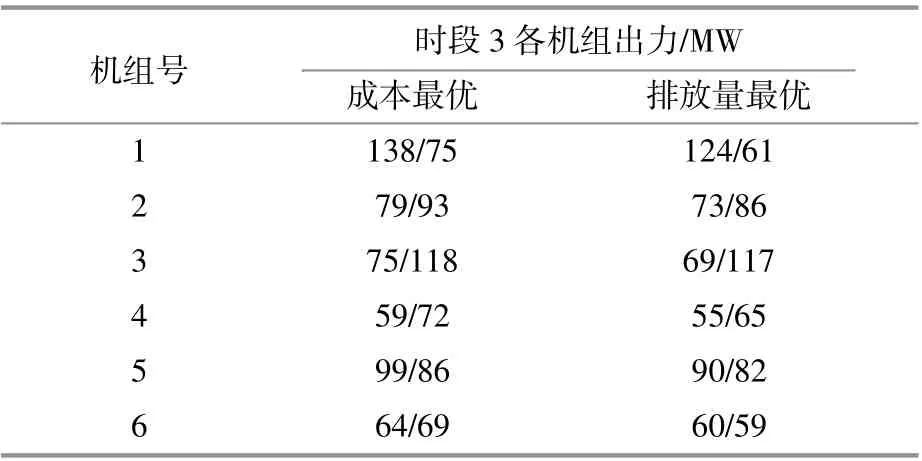
表5 不同最优模型下的机组出力分配Table5 The unit generator in the different optimal model
在表4中,当计及风能穿透功率风险时,由于受系统安全约束,风能渗透可能被置为系统风能渗透最大允许值。在表3,图4中,计及风能穿透功率风险时,当风能在系统风能渗透范围之内,对系统的调度模型影响不大,但超出范围时,风能不能全部投入系统,则影响较大。在表5中,当计及风能穿透功率风险时,由于风能渗透量的限制,常规机组出力和以往仅考虑正、负旋转备用约束模型相比,差别较大。
调度者持不同态度时,风能渗透值如表6所示。图5为在调度者不同态度下时段3的系统最优解集分布图。发电成本和排放量与系统安全系数成正比例关系[17]。

表6 不同态度下的风能渗透值Table6 Wind penetration values under different attitudes
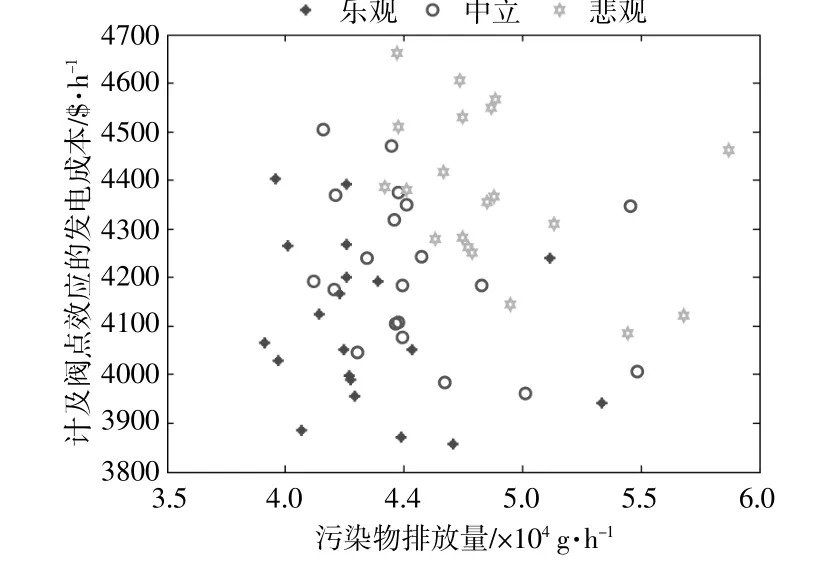
图5 调度者不同态度下的最优解集分布Fig.5 The optimal solution set under different attitude ofschedulers
由表6和图5可知,经济调度取决于调度者的不同态度,具有一定的主观性。在相同安全系数下,选择不同的系统风能渗透量最大值、系统成本和排放量,将会产生不同调度结果。系统安全水平系数越高,导致风能渗透量越少,发电成本和污染排放量会相应增加。反之同理。
图6为本文所述3种不同NSGA-2在时段1计及风能穿透功率风险下对满足模型等式约束情况对比。两种不同优化算法下的最优值对比如表7所示,对应的最优值变化曲线如图7所示。

图6 最优解集分布Fig.6 Contrast diagram of optimal solution set distribution
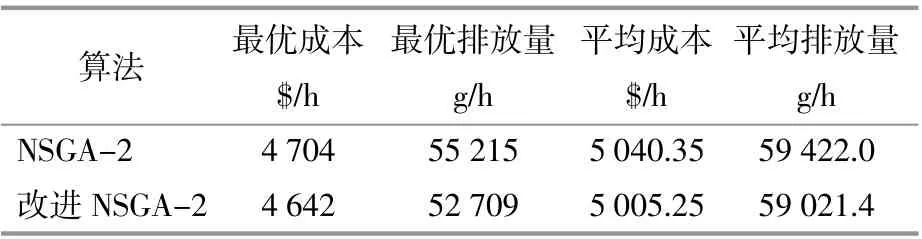
表7 两种算法性能比较Table7 The performance of the two algorithms is compared
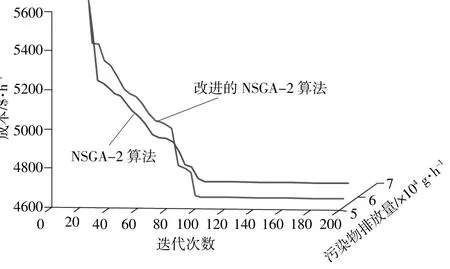
图7 最优值变化曲线对比Fig.7 Comparison graph of optimal value change curve
由图6可知:在含有等式约束的优化模型中,由于NSGA-2算法中种群的随机性,致使种群难以满足全局最优;等式约束经过机会约束规划法处理后,能较大程度的降低误差,但这也取决于调度者设置的置信水平,主观性较强;而采用本文所提的改进NSGA-2算法,能有效解决等式约束求解问题,这也说明了本文所提方法的有效性。对比表7和图5发现,本文提出的基于改进NSGA-2算法相比传统遗传算法,具有较强的全局搜索能力和收敛速度。这主要是因为采用改进的精英保留算子不仅增加了解的多样性,而且在选择精英个体时,选择性地淘汰了等级较高的个体,这大大增加了选择个体的优越性,避免进入局部最优解,从而有利于得到全局最优解。
5 结束语
本文将系统安全风险约束引入含风电场的电力系统动态经济调度问题中,利用改进NSGA-2算法中精英保留算子,避免种群陷入局部最优解。实现了计及渗透功率风险的经济调度优化,验证了风能穿透功率风险对经济调度的影响,解决了风能穿透功率给电网造成的负面风险,确定风能的渗透范围,减少了污染物排放量。

