GASA-PSO优化算法共振稀疏分解齿轮故障诊断研究

高永新，戴忠林，秦 灿

（辽宁工程技术大学机械工程学院，辽宁阜新 123000）

齿轮箱作为重要的动力传动部件广泛应用于旋转机械，在复杂工况条件下，测得齿轮箱的振动信号往往呈现出高噪声与非平稳性[1-2]。因此，从齿轮箱的非平稳振动信号中分理处出瞬态冲击信号，通过对分离出的瞬态冲击信号进行分析提取出准确的故障信号具有重要的研究意义。

现有齿轮箱故障信号分解方法主要有集合经验模态分解[3]、固有时间尺度分解[4]等。Selesnick[5]提出信号的共振稀疏分解方法（Resonance-based Sparse Signal Decomposition,RSSD），该方法可根据信号成分的振荡次数对信号进行分解与重构，实现信号的共振稀疏分解。夏俊[6]等利用松鼠优化算法计算效率与全局寻优能力的优越性,实现对共振稀疏分解的多参数优化，从而获得故障信号的特征频率。李星，张文义，陈向民等[7-9]提出了基于信号共振稀疏分解与包络谱的齿轮故障诊断方法，实现了将冲击脉冲从齿轮振动信号中分离，进而对齿轮状态和故障进行识别；朱静等[10]提出一种基于共振稀疏快速独立分量的分析方法来诊断行星齿轮箱故障，得出的高共振分量作为虚拟通道信号，两通道信号输入固定点算法处理,选择峭度值最大的分量Z做包络谱分析，提取故障特征频率。

为解决复杂工况下齿轮箱的振动信号由周期性故障引发的振动响应与随机噪声叠加组成而引起早期微弱故障信息不明显、故障特征值难以提取的问题，本文将品质因子可调小波变换（Tunable-QWavelet Transform，TQWT）的低品质因子分量与原始信号的互关度作为遗传模拟退火算法（Genetic Algorithm Simulated Annealing，GASA）与粒子群算法（Particle Swarm Optimization，PSO）的融合算法的优化对象，提出基于GASA-PSO 优化算法的共振稀疏分解齿轮故障诊断方法。

1 振动信号的共振稀疏分解

共振稀疏分解是将振动信号的振荡次数作为分解的依据将信号分离开来。当TQWT 得到高、低品质因子为Q1，Q2的小波基函数集合SH、SL后，振动信号y经共振稀疏分解后表示为：

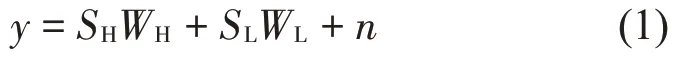
式中：WH、WL为高低共振分量系数矩阵，n表示残差分量。

共振稀疏分解通过人为经验直接给定品质因子Q与冗余因子r设计小波，由Q和r可得到尺度因子β和α如下式（2）所示：

输入振动信号中第j个子带的中心频率fc和带宽BW由下式计算：

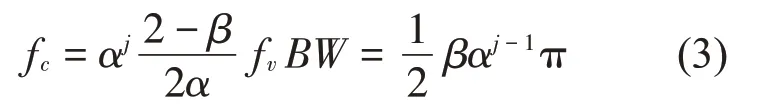
对于长度为L的输入信号，其最大分解层数由下式确定：

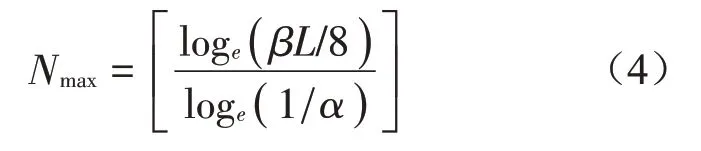
利用形态变量分析建立了耗散函数J如下式所示：

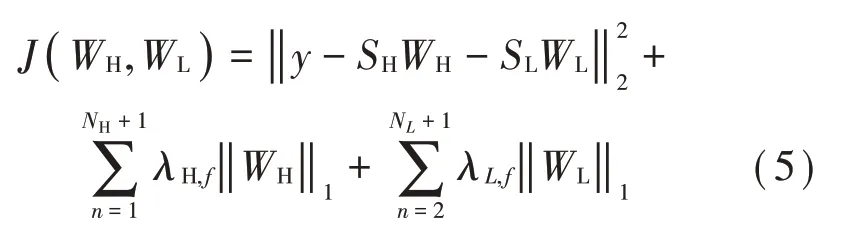
式中：λH,f、λL,f为权值系数；NH、NL为分解级数。

由于系数矩阵W的范数不可微，应用分裂增广拉格朗日算法更新迭代系数矩阵W使耗散函数J最小，从而得到最优的系数矩阵WH*和WL*[11]。

应用RSSD 方法对输入信号进行分解时，由品质因子Q决定的小波基函数库是共振系数分解能否取得理想分解效果的基础[12-13]。传统的RSSD 通过先验知识给定品质因子Q的值，主观性强，无法保证给定最优匹配因子，建立最优小波基函数库，从而影响分解效果。

2 GASA-PSO优化的共振稀疏分解

由上述分析可知Q品质因子的选取对RSSD 的分解效果起着重要作用。针对上述不足，本文提出GASA-PSO 融合算法选取TQWT 分解重构后的低共振信号与初始信号的互相关度即低共振分量峭度为融合算法的目标函数，对品质因子Q的选择过程进行优化。

齿轮早期微弱故障特征存在于低共振分量中，低共振分量相关峭度计算公式如式（7）所示：

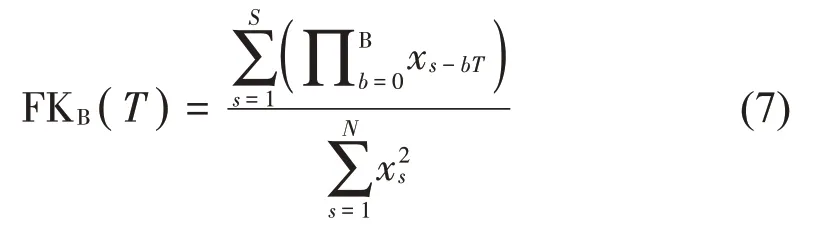
式中：x为信号源；S采样长度；T为故障脉冲信号周期；B为采样周期偏移数。

为避免因故障脉冲信号与采样长度S差距不大而造成的高低共振分量信号混淆，导致分离效果差的问题，引入两个信号的相关系数F做如下约束：

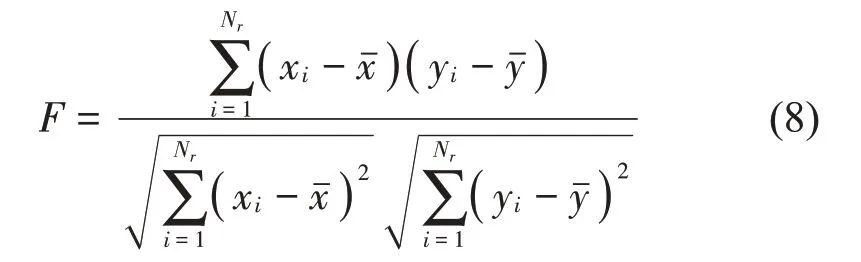
因此，本文选取经低共振分量与相关系数F做比值后的K作为适应度函数，式（7）、式（8）可得到共振稀疏分解的优化目标适应度函数：

GASA 算法在设置好退火平衡条件等操作后，GASA算法需经较多迭代次数后得到最优个体需要较长的计算时间且分离效果较差。为精确分离齿轮箱早期微弱故障信号，将GASA 算法与寻优速度较快的PSO算法融合，并作出如下改善：

（1）融合算法的底层利用GASA 的全局搜索能力来计算初代种群粒子的适应度，对较大的适应度粒子进行退火操作。上层利用PSO算法的局部搜索能力，将底层精英群体作为PSO 初代种群。设定在第q次迭代过程中，粒子i的适应度之差如下式所示：

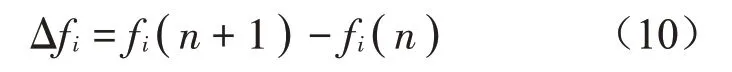
（2）上层PSO算法更新迭代计算下一代粒子的适应度，利用GASA 引入时变温度T（t），使粒子群算法具有接受次最优解得可能，迭代更新后的适应度被接受的概率P计算方法如下：

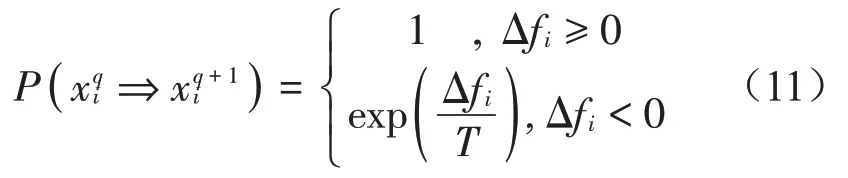
（3）惯性权重因子ω影响PSO 算法的寻优性能，当PSO 迭代次数增加、ω值线性减小时，PSO 寻优效果最好。设K为最大迭代次数，则ω的取值为：

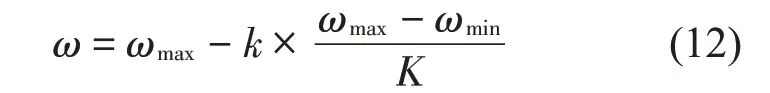
融合后的GASA-PSO 算法既具备了快速收敛的能力，又具有了全局寻优能力。在GASA 得到精英群体的基础上，经PSO算法搜寻最优解，提高齿轮早期微弱故障信号的分离效果。融合算法的步骤如下所示：

融合算法步骤如下：

（1）设置QH在0～30之间取值，QL在0～10之间取值。保持QL区间不变，截取QH从而建立C个种群。

（2）设置初始温度，初始解的状态，种群数量为50；交叉概率0.25；变异概率0.008；达到最大遗传代数300 后，以Tn+1=αTn的形式进行退火操作，选取精英个体。

（3）初始化精英群体粒子速度，最大迭代次数300，设置粒子群个体选择条件，同样以可调品质因子小波变换的低品质因子分量与原始信号的互关度作为个体适应度，

（4）判断是否可以终止，若终止，输出结果，若不可终止，替换个体，重复上述步骤。

采用融合GASA-PSO 对RSSD 的品质因子Q的选择过程进行优化，能够消除传统RSSD 方法的不足，提高齿轮早期微弱故障信号的共振分量的分离效果。

3 仿真分析

为验证本文所提方法的可行性，以齿根裂纹故障为例，分析GASA-PSO 融合优化算法的共振系数分解故障诊断方法的有效性。

3.1 齿轮裂纹故障信号振动特性分析

齿轮传动过程中正常和异常状态下振动信号有较大的差异。为验证基于GASA-PSO 算法的共振稀疏分解提取故障冲击响应的有效性，将齿轮振动信号啮合频率的分量作为齿轮故障信号[14]。

当齿根发生裂纹故障，固有频率与啮合频率作为振动信号的载波，振动信号的幅值调制和频率调制皆为转频调制[15]，故障齿轮振动信号响应表达式为：

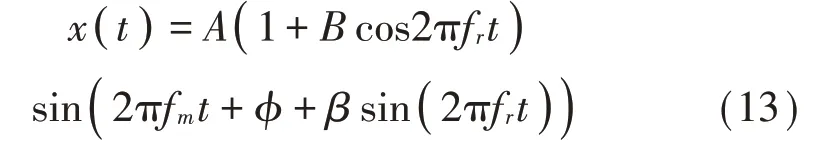
式中：B为幅值系数；β为频率系数；fr为故障轴转频。

设置齿轮箱中为一对相互啮合的齿轮，输入轴齿轮的齿数为19，输出轴齿轮的齿数为48。电机转速为1 800 r/min，输入轴的频率为30 Hz，啮合频率为570 Hz，采样频率为10 000 Hz。采用MATLAB软件中的ode15 s 法求解齿轮箱动力学方程可得到齿轮箱系统的动力学响应[16]。

对比观察图1中2幅频谱图可以发现：频率主要成分是齿轮副的啮合频率fm及其倍频2fm、3fm等，各倍频之间存在边频带，随着裂纹深度的增加，其倍频幅值增大，边频带在各个倍频间的振荡明显，幅值增大。

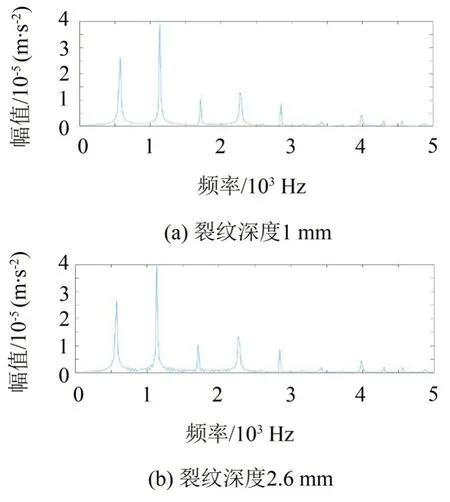
图1 不同裂纹深度主动轮的频域图

由上述分析可知，可根据边频带的分布区间和幅值判别齿根裂纹故障程度，为齿轮副的早期微弱故障诊断提供理论支持。

3.2 信号仿真分析

在进行齿轮箱故障诊断时，采集的齿轮裂纹故障特征信号中裂纹等故障信息会以周期性冲击脉冲的响应的形式表现，根据分析发现此脉冲的频率一般为齿轮转频或其倍频，因此，以此作为故障特征的基准进行提取。根据上文分析的齿轮箱齿根裂纹故障，利用MATLAB以上文故障齿轮振动信号模型来验证GASA-PSO 融合算法优化后共振稀疏算法对齿轮故障振动信号分离的有效性。设置一组衰减系数为-420，载波频率为520 Hz，调制频率为100 Hz的周期性衰减脉冲信号，对该信号设置两组幅值为3 mm/s2和2 mm/s2，频率为1 560 Hz与1 380 Hz的正弦信号进行调制，调制后信号如图2所示：

图2为进行调制处理的正弦信号和随机噪声叠加信号，无法分析脉冲信号的特点。如图3 所示为采取融合算法优化的共振稀疏分解处理后的高、低共振分量信号及残差分量信号。齿轮箱早期微弱故障信号特征主要存在于低共振分量信号中，故对此分量信号做希尔伯特变换后，利用findpeaks 函数提取调制后信号中故障特征，绘制包络谱图如图4、图5所示。

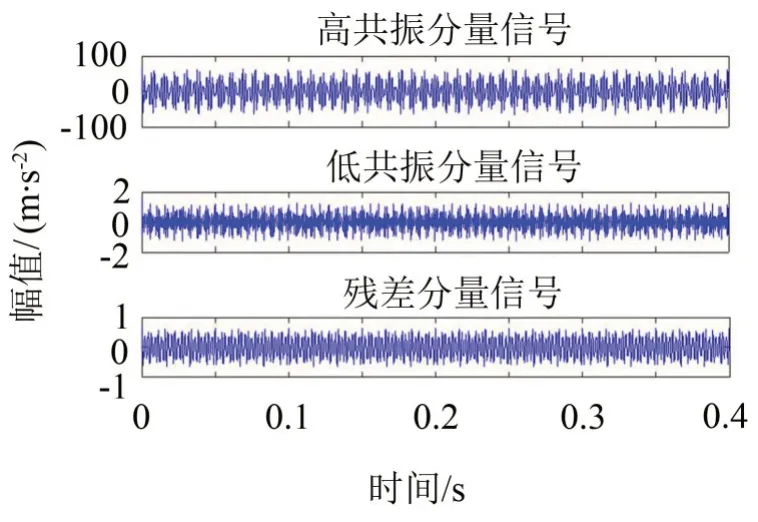
图3 模拟仿真信号分解后各分量时域波形图

如图4所示，高共振分量主要由频率为1 380 Hz和1 560 Hz的两组正弦信号叠加而成。

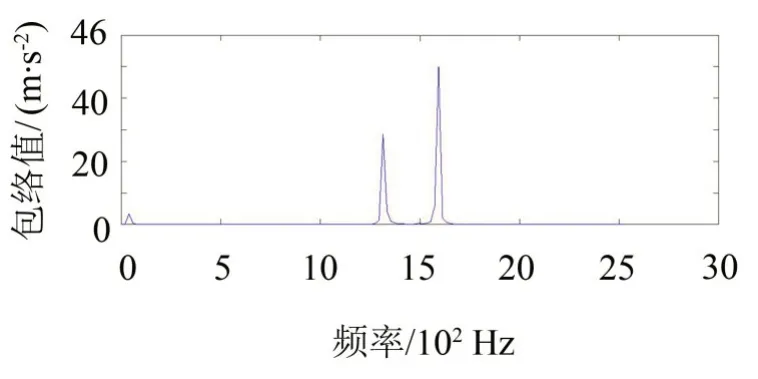
图4 GASA-PSO高共振分量的频谱分析

如图5至图6所示，振动信号的低共振分量经过频谱分析后可直观地发现，GASA-PSO 优化算法低共振分量包络谱中含有调制频率为100 Hz 的脉冲信号及其倍频，与GASA 算法优化后的低共振分量包络谱相比，周期性冲击清晰可见，分离效果较好，整体的规律性较强，与理论贴合度较高。该方法能够依据高、低共振分量故障特征频率准确地分离出故障特征，从而对早期齿根裂纹故障进行诊断。

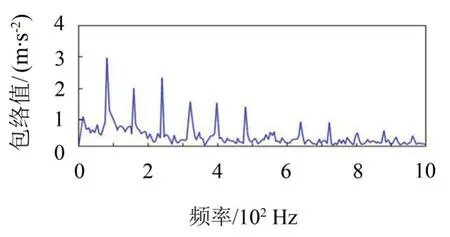
图5 GASA-PSO 优化算法低共振分量包络变换谱

图6 GASA优化算法低共振分量包络变换谱

4 实验分析

4.1 实验设计

为验证基于GASA-PSO 融合算法的共振稀疏分解的风机齿轮箱故障特征提取方法的有效性，设计如下实验方案：

平行轴齿轮箱故障数据实验测试平台如图7所示，将存在裂纹故障的齿轮安装在齿轮箱内，平行轴齿轮箱通过联轴器与变速驱动电机和磁力制动器连接，电机反装齿轮箱和联轴器驱动齿轮箱完成实验，振动加速度/速度一体化传感器测量驱动轴输入端、输出端的轴向和径向振动信号。表1给出平行轴齿轮箱齿轮传动部分齿数。

图7 平行轴齿轮箱故障数据实验测试平台

表1 平行轴齿轮箱传动参数

4.2 实验数据分析

选取驱动轴输出端测点作为振动原始信号，通过振动传感器采集到振动原始信号如图8 所示，虽可隐约看出信号中存在脉冲成分，但受其复杂工况影响，规律性较弱；对振动传感器采集到振动信号进行GASA-PSO 融合算法的共振稀疏分解特征提取后，如图8得到图9。

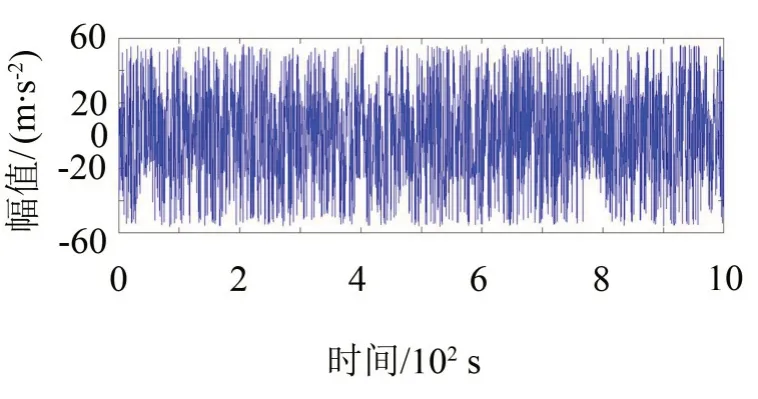
图8 振动原始信号

图9 实验信号共振稀疏分解后低共振分量包络谱

如图9 所示，采用融合GASA-PSO 优化的共振稀疏分解法可有效提取风机齿轮故障特征信息。图9低共振分量中主要包含调制频率为100 Hz的脉冲信号及其倍频信号。低共振分量包络图呈现fm及其倍频的故障频率，故障特征明显，分解效果理想。

本文所提出的GASA-PSO 优化算法的共振稀疏分解方法可实现品质因子Q与故障振动信号脉冲成分最佳的匹配，可有效地提取故障特征。

5 结语

（1）研究齿根裂纹对齿轮副振动特性的影响发现齿根裂纹故障对齿轮副的振动响应影响会随着裂纹深度的增加而越来越明显，通过观察频域图中边频带的分布区间和幅值可以判别齿根裂纹故障的严重程度。

（2）品质因子的选取在共振稀疏分解的过程中有着重要的作用，会影响分离齿轮故障信号的瞬态冲击信号的效果。利用融合GASA-PSO 算法底层的全局寻优与上层的局部寻优从而获得更好的寻优效果，在可取的范围自适应选择最匹配品质因子是行之有效的方法。通过仿真试验与实验的方法证明，该算法具有较好的抗噪性，能够准确地分解信号，进而提取复杂信号中的故障信息，为故障诊提供依据。