气磁轴承支承高速电主轴的协同控制

竺志大,唐率,寇海江,柴青,曾励

(扬州大学 机械工程学院，江苏 扬州 225127)

高速电主轴的轴承配置主要有滚动轴承、液体(气体)静压轴承和磁悬浮轴承：滚动轴承高速电主轴的成本低，但转速也相对较低，噪声大且精度、寿命、可靠性都有局限；液体静压轴承高速电主轴的刚度高，存在液体摩擦，驱动功率损失比滚动轴承大，主轴在高速工况下的温升和热变形控制比较困难[1〗； 气体静压轴承高速电主轴回转精度和承载刚度高，存在高速涡动和气锤振动等现象[2-3]；磁悬浮轴承高速电主轴极限转速高，无摩擦，可进行刚度和阻尼主动控制，但刚度小，承载力及精度相对较低[4-5]。

基于气体静压轴承精度高，可提供较大承载能力以及磁悬浮轴承具有良好可控性的特性[6-7]，提出一种新型的高速精密气磁悬浮混合轴承，气体轴承起主要承载作用，磁悬浮轴承辅助承载并实时控制系统的刚度和阻尼，从而实现气磁轴承高速电主轴回转精度和承载刚度高且稳定可控的综合性能。

气磁轴承的控制系统较为复杂，PID控制灵活性较高，但参数可移植性差，工作量大，流程复杂，系统稳定性等也存在不足[8-12]。协同控制理论是现代数学与协同学交叉融合的新理论，采用状态空间法，通过定义流形和控制综合设计控制器，适用于多维、高度耦合的非线性系统[13-14]，在永磁同步电动机上实现了电动机系统的线性化并有效降低了系统阶数[15-16]，在磁悬浮轴承上有效地实现了各个自由度位移的精确控制，并可以保证转子质心位移的准确性，响应速度快且无超调[17-19]：因此，尝试将协同控制理论应用于气磁轴承的控制，使电主轴的稳定性更好，精度更高，并通过仿真与试验验证其可行性。

1 气磁轴承支承的高速电主轴系统

1.1 高速电主轴结构

气磁轴承高速电主轴模型如图1所示，一组径向气磁悬浮轴承上装有传感器，及时检测主轴位移变化，通过反馈系统调节气磁悬浮力，使主轴回到径向平衡位置；一组辅助轴承(推力球轴承)用于保证主轴轴向平衡。

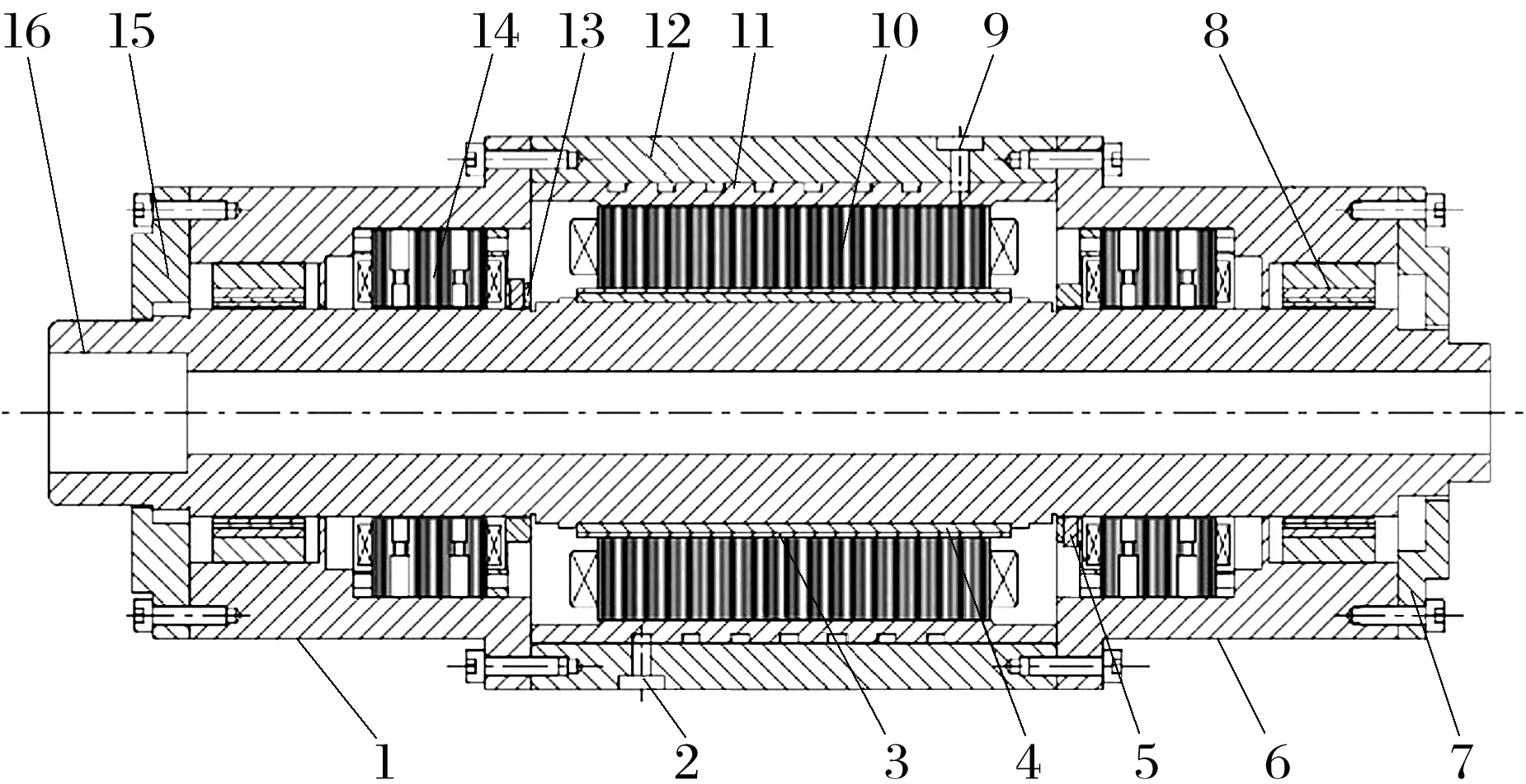
1—前轴承座；2—冷却套进水口；3—保护套；4—永磁片；5—传感器； 6—后轴承座；7—后端盖；8—辅助轴承；9—冷却套出水口；10—电动机定子；11—冷却套；12—电动机外壳；13—传感器外壳；14—径向气磁悬浮轴承；15—前端盖；16—电主轴。

1.2 气磁轴承工作原理

气磁轴承的结构如图2所示，静压气体轴承部分在外界恒定气压供气下起到主轴启动及正常工作时的承载作用，主动磁悬浮轴承根据位移传感器反馈信号改变线圈电流的大小，调节主轴与轴承的间隙。气磁轴承的工作原理如图3所示。外界气体通过供气装置和球阀进入气动三联件(空气过滤器、减压阀和油雾器)，然后经供气孔进入气体腔室，再由节流孔进入轴承与主轴之间。气体经过节流孔会产生一定的压降，由轴承两端流出时降为大气压，轴承与主轴之间会产生具有承载能力的气膜，从而使主轴稳定悬浮。当受到外界干扰时，磁悬浮轴承中的传感器接收到信号，计算偏转方向的位移并将位移信号传输至控制器，由控制器转变为电信号传输至功率放大器中改变轴承线圈上的电流大小，实现对主轴系统的反馈控制调节。气磁轴承结构参数见表1。

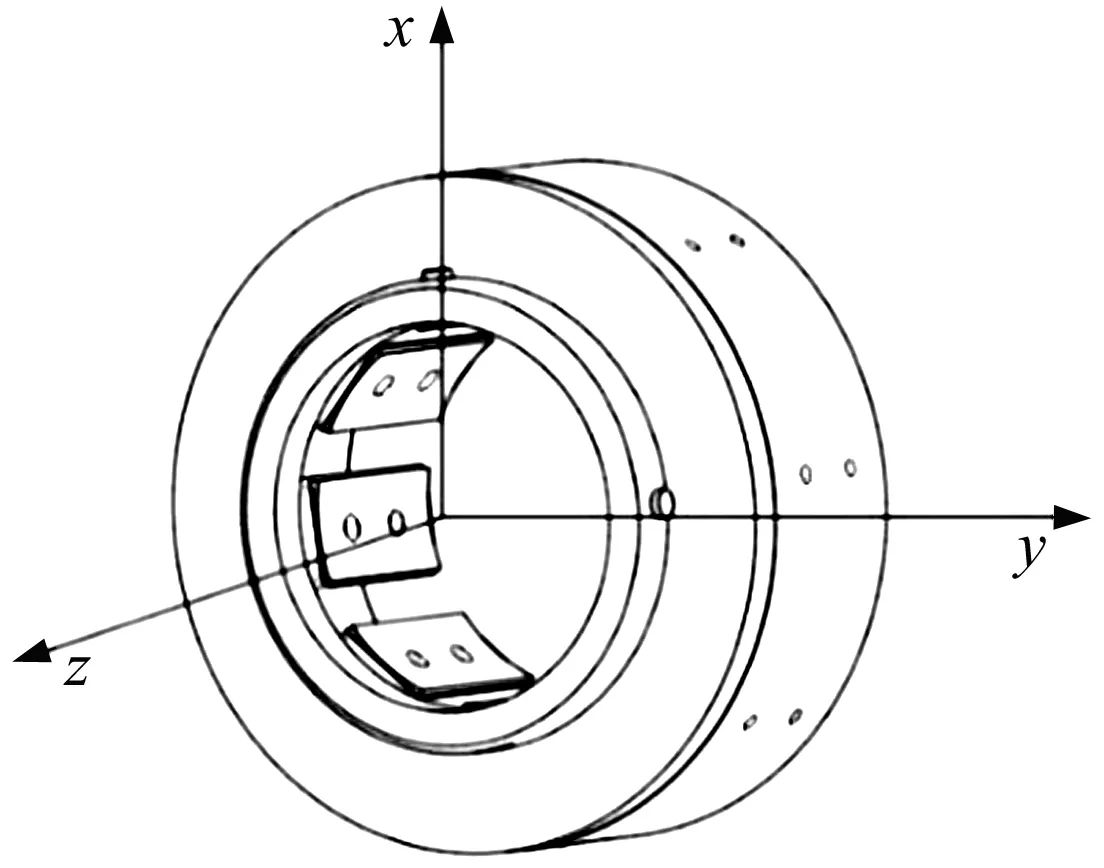
1—传感器外壳；2—气体腔室；3—节流孔；4—排气孔；5—径向线圈；6—供气孔；7—传感器。

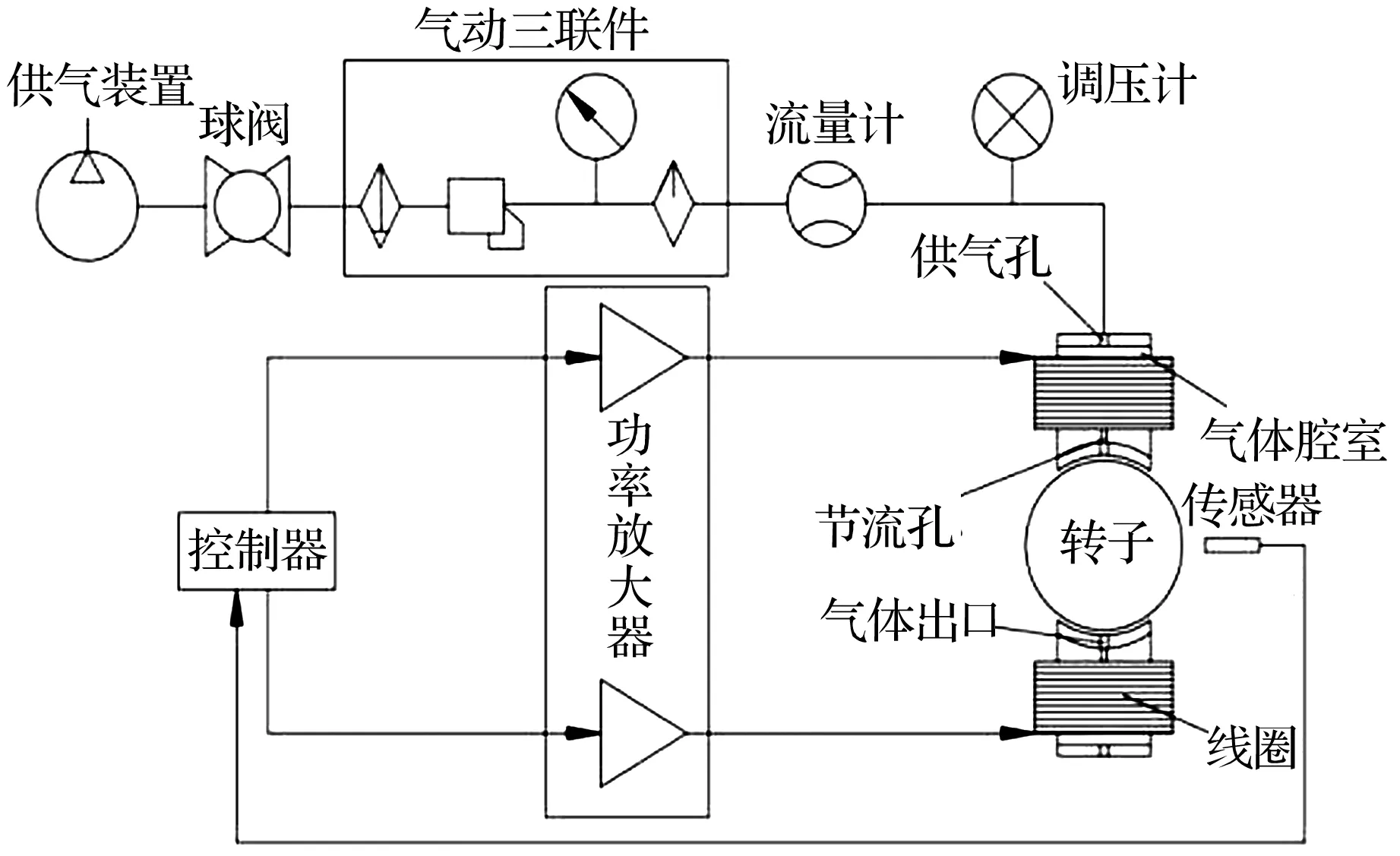
图3 气磁轴承的工作原理

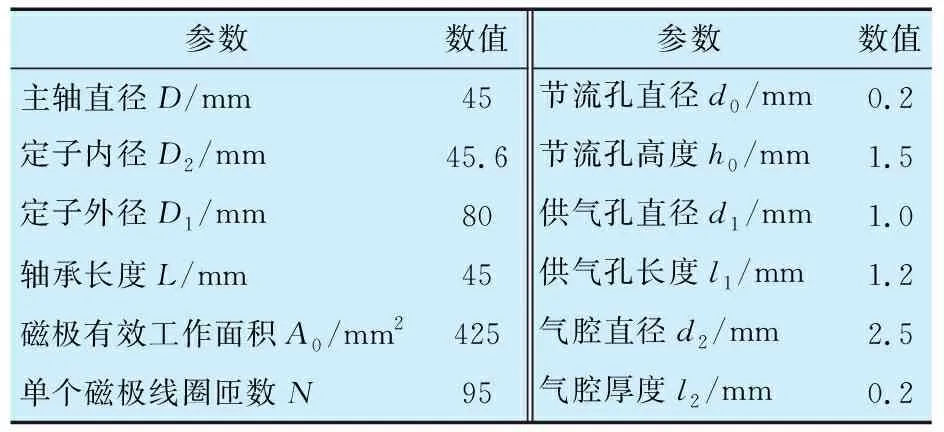
表1 气磁轴承结构参数

1.3 气磁轴承-主轴系统动力学模型

不考虑重力及外部阻力的情况下，建立四自由度径向气磁轴承-主轴系统的简化模型，如图4所示：fax，fbx为气磁轴承A，B在x轴方向的电磁力；f1ax，f1bx为气磁轴承A，B在x轴方向的气体承载力；fay，fby为气磁轴承A，B在y轴方向的电磁力；f1ay，f1by为气磁轴承A，B在y轴方向的气体承载力；xa，ya，xb，yb为主轴在a，b点上x，y轴方向的位移；xc，yc为主轴质心c在x，y轴方向的位移；α，β为主轴绕其质心c处x，y轴的角位移；ω为主轴绕z轴的转动角速度。

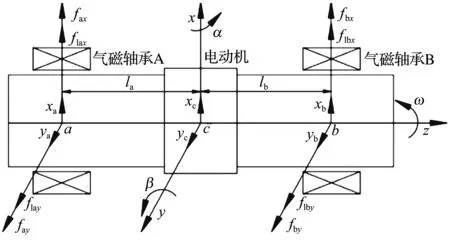
图4 气磁轴承主轴系统简化模型

根据主轴系统动力学理论，该简化模型的动力学方程为

(1)

将上述方程进行矩阵化并代入参数可得气磁轴承的动力学方程为

(2)

其中

式中：m为主轴系统的质量；Jx，Jy，Jz为主轴绕x，y，z轴的转动惯量(Jx=Jy)；la，lb为气磁轴承A，B中心到主轴质心c的距离(la=lb)；M为质量(转动惯量)矩阵；XC为位移(角)矩阵；G为陀螺矩阵；Cq为气体阻尼矩阵；Kq为气体刚度矩阵；Ks为位移刚度矩阵；Ki为电流刚度矩阵；c1a,c1b为气磁轴承的阻尼；k1a，k1b为气磁轴承的刚度；ksax，ksbx，ksay，ksby为气磁轴承的位移刚度；kiax，kibx，kiay，kiby为气磁轴承的电流刚度；If为电流矩阵；iax，ibx，iay，iby为气磁轴承A，B在x，y轴方向上的线圈电流。

取气磁轴承-主轴系统的状态变量为

(3)

则轴承-主轴系统的输入变量为

U=[u1,u2,u3,u4,u5] =[uax,ubx,uay,uby,Me]，

(4)

系统的输出变量为

Y=[y1,y2,y3,y4,y5]T=[xa,xb,ya,yb,ω]T，

(5)

综上，气磁轴承-主轴系统的状态方程为

(6)

J=Jx=Jy，

式中：Me为外力输入转矩。

2 气磁轴承-主轴系统协同控制仿真分析

2.1 构建主轴系统宏函数[17]

设轴承-主轴系统的状态方程为

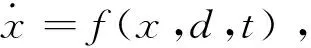
(7)

式中：x为系统的状态变量；d为系统的控制变量；t为时间。

设计控制器前要定义宏变量ψ(x,t)，其是x的函数，为x1～xn的线性组合(n为系统的维数)。系统宏变量的个数需与系统控制输出个数一致。

系统流形定义为

ψ(x)=0，

(8)

可使系统逐渐收敛到流形的方程为

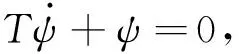
(9)

式中：T为时间常数，其数值可根据实际计算自行决定，T越小，收敛速度越快。

将宏变量ψ(x,t)和x(t)对时间复合求导可得

(10)

将(7)式和(10)式代入(9)式得

(11)

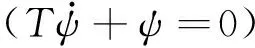
构建气磁轴承-主轴控制系统的宏函数，需对主轴径向的4个自由度进行控制，共计13个状态变量，但只有x9～x13这5个状态变量的微分方程包括输入变量，确定气磁轴承-主轴系统的宏变量组为

(12)

则主轴系统的协同控制规律为

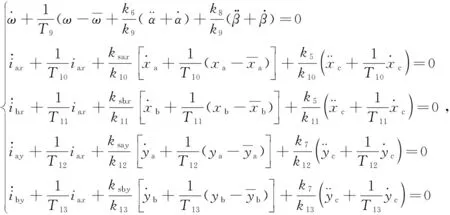
(13)

xa=x1-lax4=y1，xb=x1+lbx4=y2，ya=x3+lax2=y3，yb=x1-lbx2=y4，ω=y5，

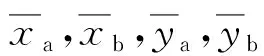
2.2 气磁轴承-主轴系统协同控制

根据协同控制模型，结合主轴系统动力学模型，可得主轴系统的非线性协同控制模型，径向四自由度非线性气磁轴承支承主轴系统协同控制仿真模型如图5所示，模型参数见表2。协同控制下，主轴质心位移响应仿真结果如图6所示。

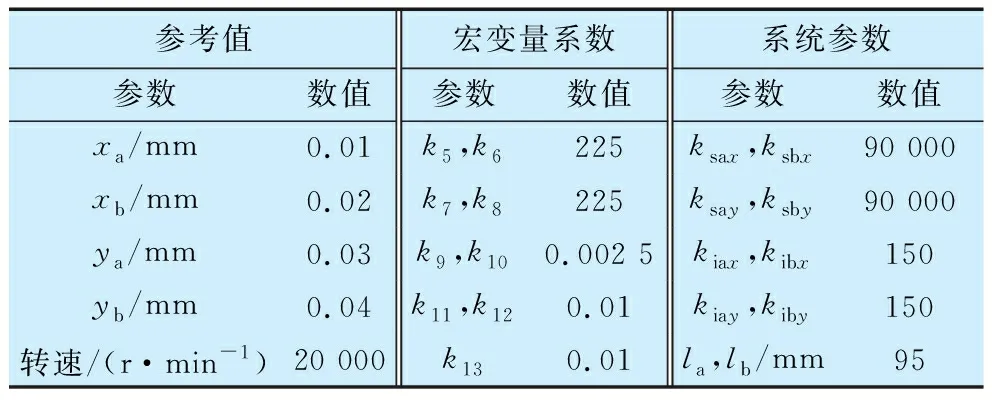
表2 气磁轴承-主轴系统控制参数

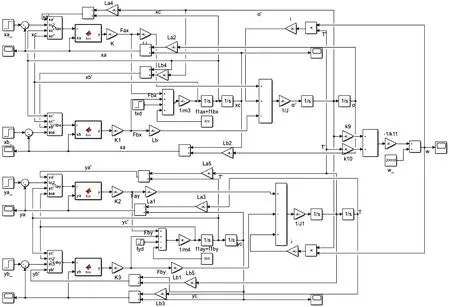
图5 径向四自由度非线性气磁轴承主轴系统协同控制仿真模型

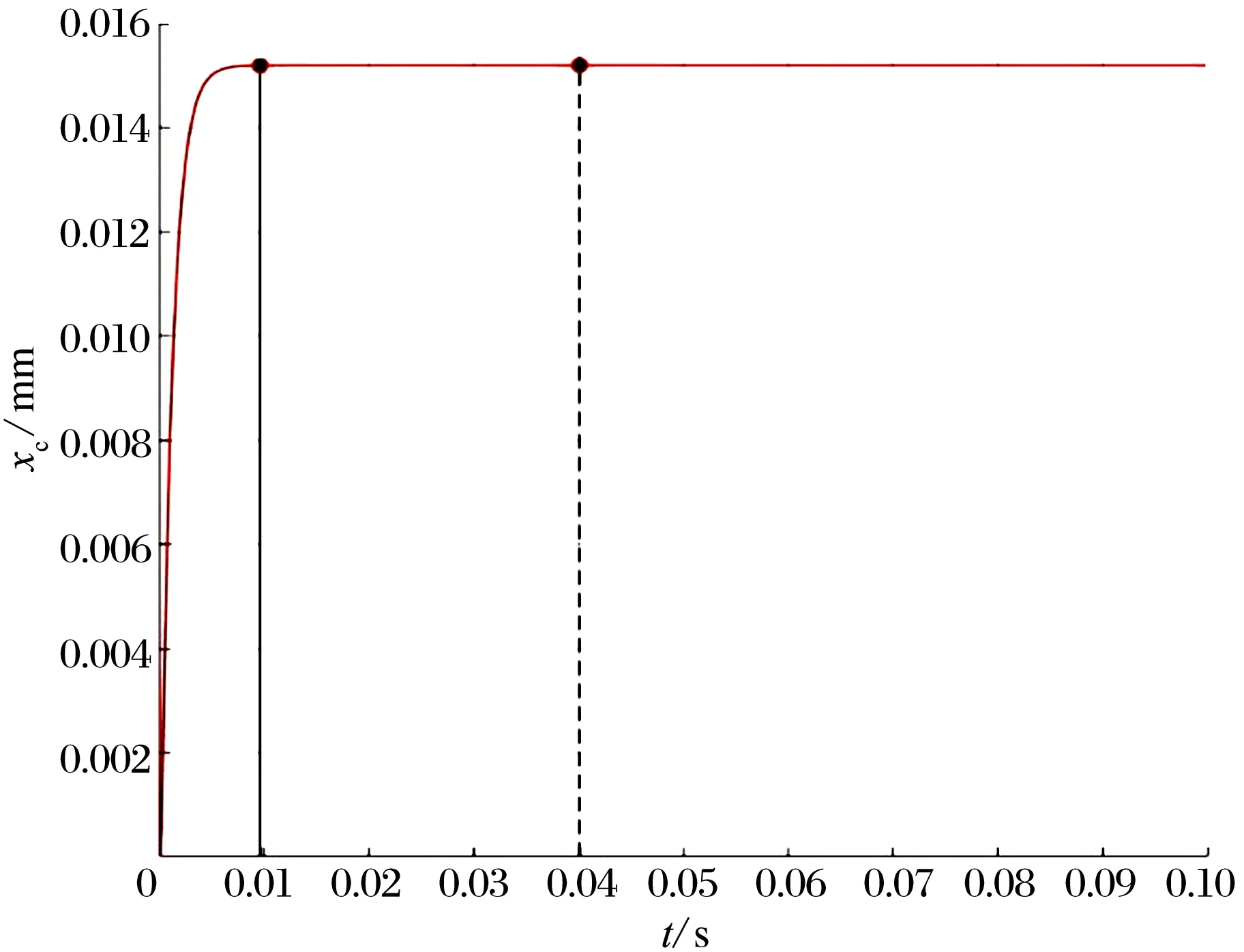
理论质心位移与仿真质心位移之间的误差为

(14)

由表3可知，主轴质心位移仿真值与理论值的误差为0.000 2 mm。在协同控制下，可通过控制径向气磁轴承在x，y方向上的位移，使主轴质心位移在较短的时间内到达平衡位置。

表3 主轴质心位移仿真与理论计算结果

2.3 协同控制与PID控制对比分析

电流、电压、时间常数和权系数与协同控制性能相关，协同控制与PID控制的参数见表4。当主轴-轴承系统不存在外界干扰力时，协同控制与PID控制下的主轴质心位移仿真结果如图7所示：协同控制下，主轴质心位移能够平稳、无超调的到达给定位置且响应速度快；PID控制下，出现了超前和超调现象，响应时间比协同控制滞后0.03 s，控制效果不如协同控制。

表4 协同控制与PID控制参数

在0.04～0.06 s给主轴0.05 N的脉冲干扰力，协同控制与PID控制下的主轴质心位移响应特性如图8所示：协同控制下，在0.04 s加入干扰时，主轴质心产生约0.002 mm的微小位移但一直处于稳定状态，在0.06 s撤去干扰后，协同控制用时约0.002 s就使主轴质心稳定下来并回到原来的平衡位置；PID控制下，加入干扰后主轴质心位移波动范围较大且超出最大轴承间隙，极易发生碰撞，撤去干扰后用时约0.015 s才使主轴质心回到平衡位置，抗干扰能力弱于协同控制。

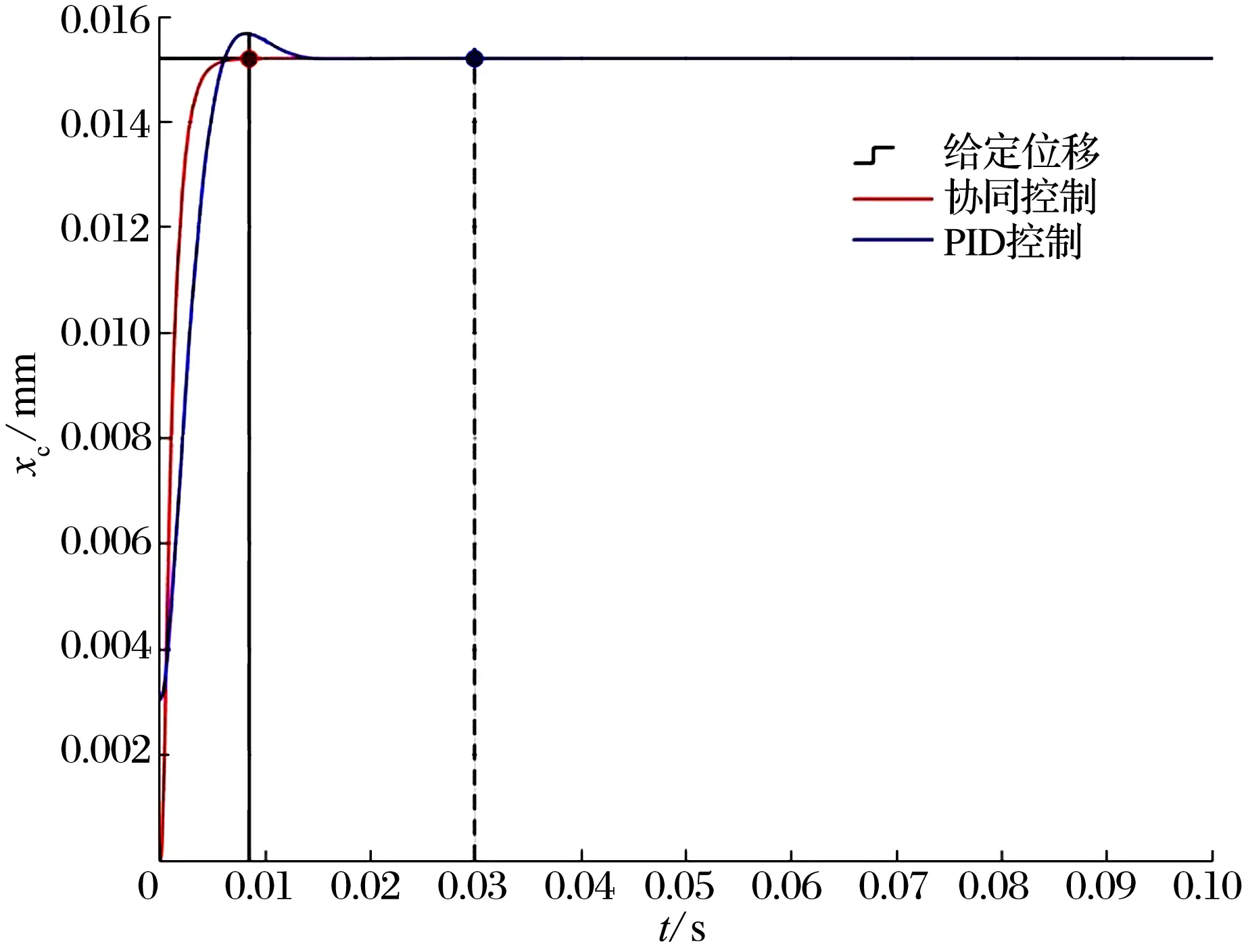
图7 协同控制与PID控制下主轴质心位移的对比

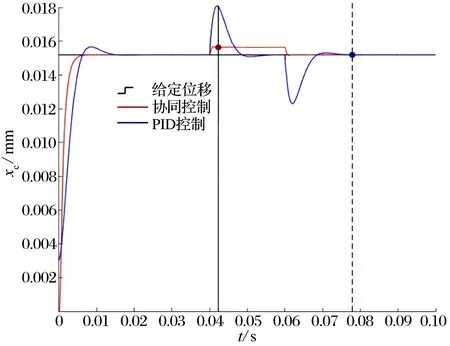
不同转速(20 000，30 000 r/min)下，协同控制与PID控制的仿真结果如图9所示：协同控制下，到达给定转速的时间都比较短(约0.007 s)且平稳无超调；PID控制下，虽然也没有出现超调现象，但到达给定转速的时间协同控制滞后约0.03 s。

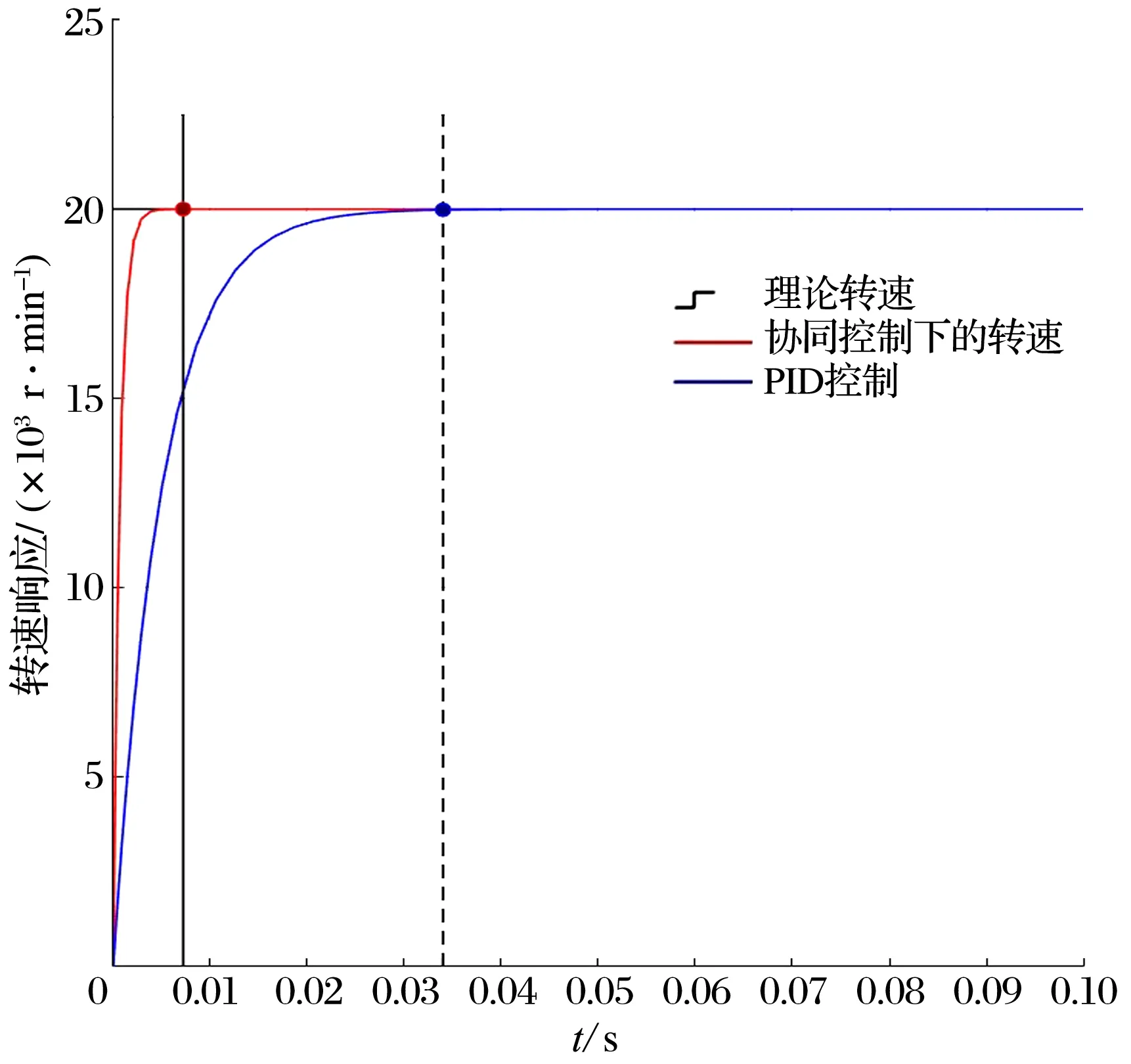
(a)20 000 r/min

综上分析可知，协同控制的各项性能均优于PID控制。

3 气磁轴承主轴协同控制试验

3.1 控制系统硬件设计

基于DSP TMS320F28335的数字控制原理如图10所示：电涡流位移传感器实时检测主轴位移信息，电流传感器实时检测电磁铁线圈电流；初始状态，DSP控制器处于未工作状态，此时位移未发生变化；主轴运转时，控制位移与给定位移的模拟信号经A/D转换器变为数字信号，控制芯片计算出两者之间的差值δ并通过智能控制算法计算出差值对应的电子信号量M，经过DSP处理后输出PWM波并通过光电隔离驱动输送到功率放大器，由功率放大器输出电信号，改变轴承线圈中的电流，调节主轴与轴承之间的间隙，直至主轴回到平衡位置。

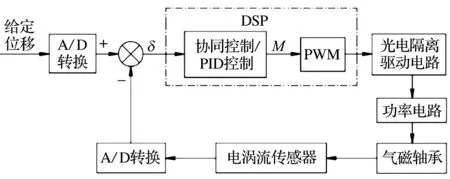
图10 DSP控制原理图

3.2 协同控制算法的实现

协同控制算法框图如图11所示，取气磁轴承A在x方向上的电流为例研究协同控制规律，其表达式为

(15)

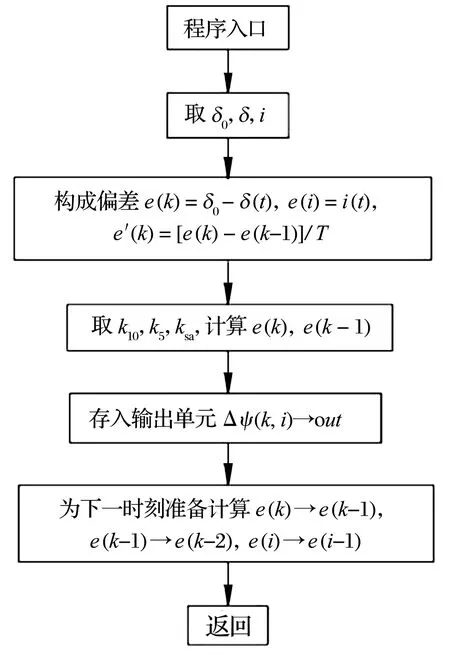
图11 协同控制算法框图

离散化后可得

(16)

(17)

其中

式中：i为电流；k为位移；ksa为位移刚度系数，由轴承结构决定；k10和k5为算法参数，通过大量调试后取一组最佳数值。

3.3 气磁轴承主轴悬浮试验

气磁轴承电主轴试验原理图如图12所示，气磁轴承控制器、电动机控制器分别控制气磁轴承和电动机，V/F变频器用于调节电主轴转速，传感器检测电主轴位移变化，数据采集仪采集位移变化信息并将采集数据输送到计算机进行数据处理。

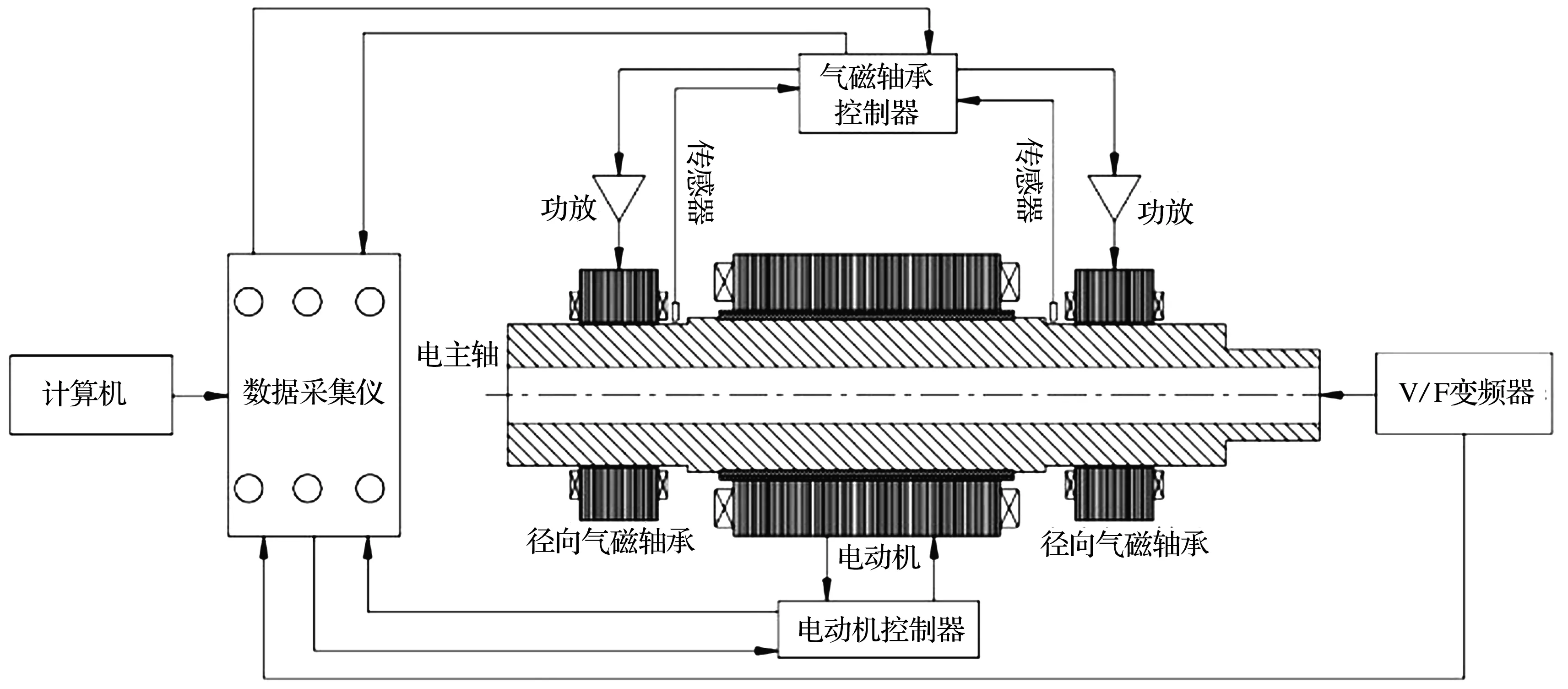
图12 气磁轴承电主轴试验原理图

初始状态，先向电主轴施加预应力(代替气体力支承效果)以保证主轴在非平衡位置稳定悬浮，然后给线圈通入电流使主轴迅速回到平衡位置，此时电涡流传感器实时检测主轴位移变化过程并记录数据。

电主轴启动悬浮的位移曲线如图13所示：电主轴在短时间内均到达平衡位置，并在平衡位置附近波动；PID控制下，主轴位移出现超调现象且波动较大，波动范围为-0.004 5～+0.007 5 mm；协同控制下，主轴位移启动平稳、无超调，约0.015 s就到达平衡位置且波动较小，波动范围约-0.002～+0.002 mm，振幅远小于PID控制，控制效果更好。

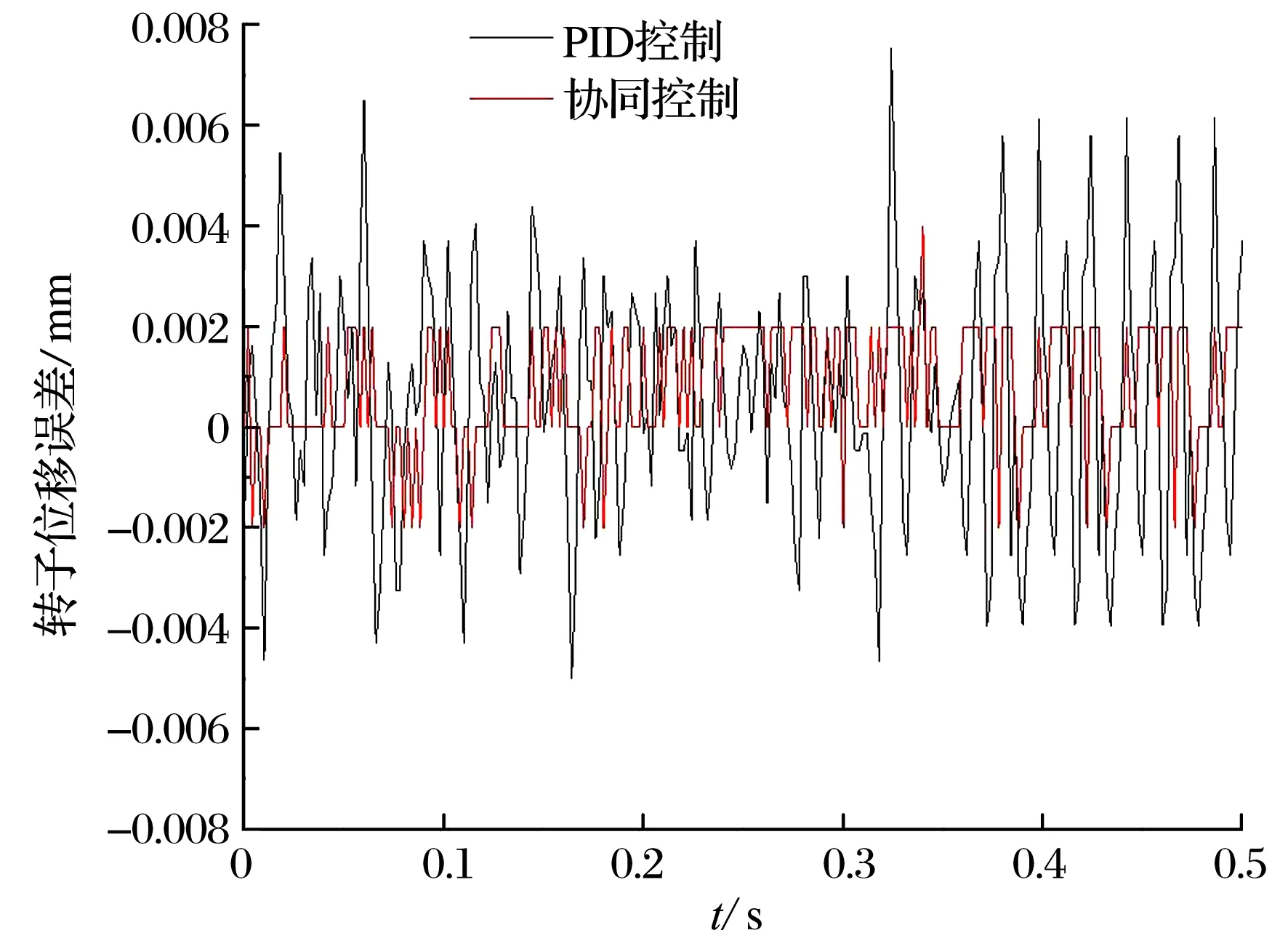
图13 主轴启动悬浮位移误差曲线

主轴旋转过程中受到外界干扰会导致其回转精度降低，影响工件加工质量。设定主轴转速为20 000 r/min，在0.150～0.375 s加入外界干扰，观察主轴响应特性曲线，结果如图14所示：刚加入干扰时，主轴向下偏移0.025 mm，该偏移值在主轴正常波动范围之内，撤去干扰后主轴回到平衡位置。协同控制下，加入干扰后主轴浮动范围为0.05～0.10 mm，存在外部干扰期间主轴波动范围较小且很少出现尖峰时刻，撤去干扰后主轴浮动范围为-0.02～+0.02 mm；PID控制下，加入干扰后主轴浮动范围为0.025～0.130 mm，存在外部干扰期间主轴波动范围较大且多次出现超调现象和尖峰时刻，撤去干扰后主轴浮动范围为-0.03～+0.03 mm。试验结果表明，相比于PID控制，协同控制下主轴受到外界干扰时不会出现超调现象，对干扰反应不敏感，即抗干扰能力强，气磁轴承主轴系统的鲁棒性更高。

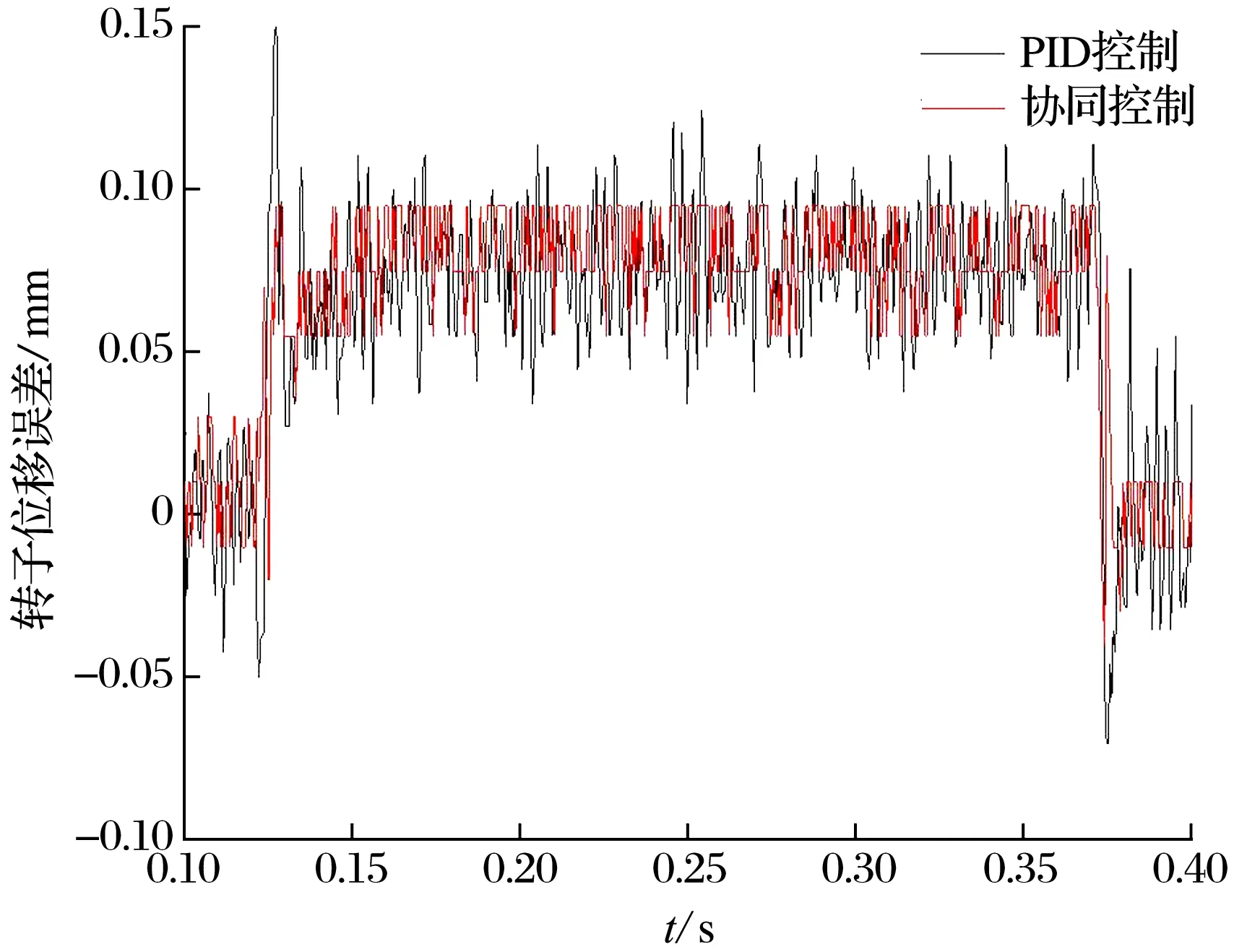
图14 主轴受到干扰时的波动误差曲线

4 结束语

针对气磁轴承结构进行优化设计并建立了新型气磁轴承主轴模型，求解了主轴系统协同控制规律，利用MATLAB/Simulink搭建径向四自由度气磁轴承支承主轴系统协同控制仿真模型，对比分析了协同控制与PID控制下的主轴位移响应特性、主轴质心位移响应特性以及转速响应特性，仿真结果表明协同控制优于PID控制。

搭建了气磁轴承主轴系统试验平台，设计了控制算法并进行了主轴悬浮试验，结果表明协同控制能够使主轴稳定且无超调地到达平衡位置，协同控制下的主轴系统具有更高的回转精度和控制精度，且静动态性能和鲁棒性更好。