储能电池一次调频无模型自适应控制策略

廖世强，张新燕,2，刘莎莎，张光昊，黄利祥，施 锐

（1新疆大学；2可再生能源发电与并网技术教育部工程研究中心，新疆维吾尔自治区 乌鲁木齐 830047）

随着新能源在电网中的占比不断升高，且新能源的输出功率具有随机波动性[1]，降低了电力系统频率的稳定性[2]，对电网调频提出了更高要求[3]。由于传统火电机组调频能力不足[4]。电池储能系统响应迅速、能量可双向流动，是优质的调频资源。因此在新能源并网规模不断增加[5]、电网频率更加复杂多变的情况下[6]，储能系统参与调频的方式成为研究热点[7]。

随着能源结构转型，近几年来国内外储能电池参与调频得到快速发展，相应建立了许多示范工程[8]，因此控制系统从单一调频逐步转向考虑电池寿命、经济效益[9]、选址容量配置、自适应能力等多方面的要求。目前电池储能系统主要以定下垂和变下垂参与一次调频，两种方法均提供快速频率支撑[10]，后者有助于减小调频后期频率偏差，提高频率的稳定性[11]。文献[12]利用飞轮储能和电化学储能联合调频，其机组耦合降低了电网频率变化量。也有采用储能系统虚拟惯性与虚拟下垂控制两者结合的调频控制模式[13]，充分利用二者优势，可提升一次调频的效果，但惯量控制使频率恢复稳定时间加长。

为维持电池寿命，以及提前为下一次调频做准备，SOC作为储能电池重要的变量之一，在储能电池控制方法的研究中必须加以考虑。文献[14]提出了控制电池储能调频死区和单位调节功率关键参量。文献[15]提出一种动态权重因子的自适应控制策略，使用两种控制模式的相互结合与平滑切换，使电池得到有效保护，且不会对电网造成冲击，但对储能系统的数学模型依赖较高。文献[16]总结了储能电池运行效率和寿命评估的一些建模方法，文献[17]提出基于调频和SOC恢复分段式调频策略，侧重于电池SOC保持效果，未充分让其参与到调频，文献[18]基于调频、经济效益、安全对电池寿命进行研究，为电池储能SOC的最优使用范围提供参考。文献[19]兼顾电池储能系统SOC与电网功率需求，提出基于SOC的动态可调下垂控制。文献[20]提出一种虚拟正惯量和虚拟负惯性两者结合的控制方法，可降低最大频率偏差，且使频率快速稳定在一个范围内，但考虑的工况简单，自适应力不强。

综上，在现有研究中，缺少一种既能改善频率恢复，同时又能将SOC 维持在最优使用范围内且能自适应实时负荷波动的控制策略。且控制策略的设计很大程度上依赖储能系统的精确数学模型。

无模型自适应控制(model-free adaptive control，MFAC)由侯忠生教授[21]提出，其是一种典型的利用数据驱动的控制方法，仅需要使用被控系统的输入输出数据进行控制器的设计分析，摆脱对被控对象数学模型的高度依赖，将动态非线性系统利用数据及算法得到其动态短时线性化函数，得到被控系统的动态模型，模型的某些关键参数也通过反馈算法动态调整，从而达到控制效果理想，自适应度高的效果。MFAC方法已经成功应用在风力发电机载荷控制[22]、城市道路交通控制[23]、自动泊车控制[24]、新能源并网控制[25]、新能源电力系统频率协调控制[26]等领域。

基于此，本文结合了储能电池的特点，研究了含储能电池的区域电网频率特性模型，充分考虑储能参与调频的多方面要求以及摆脱对储能系统的精确数学模型依赖，提出基于SOC 保持效果的无模型自适应控制策略，将电网频率和SOC 作为控制器的输入，实时调整储能电池出力。最后建立区域电网调频算例进行仿真验证。

1 含储能的电力系统调频特性分析

1.1 无新能源渗透率的区域电网调频模型

含储能的区域电网频率模型是一个闭环控制系统。本文目标是研究区域电网总体调频特性，所以不考虑频率的功角稳定与分散性问题，同时忽略二次调频环节。根据电力系统经典文献[27]，基于区域等效方法，聚合的区域电网的调频模型如图1所示。

图1 无新能源的区域电网调频模型Fig.1 Frequency modulation model of power system without new energy

为简化分析，仅考虑电网负荷的情况下，区域电网频率特性模型传递函数为

式中，M= 2H，H为惯性常数；D为阻尼常数。

1.2 计及新能源渗透率的电区域电网调频模型

对于高占比新能源的区域电网系统，需要在上述模型中体现渗透率的加入。假设新能源机组同比例替代火电机组，新能源机组占比(渗透率)为p时，惯性常数和其频率特性传递函数见式(2)、(3)：

在图1模型的基础上，建立各个部分的数学模型[28-29]，体现新能源渗透率的系统模型如图2所示。

图2 中，-KG为火电机组的单位调节功率；Kb为储能电池的单位调节功率；ΔPL(s)为负荷功率波动量；ΔPb(s)为储能电源出力；ΔF(s)为电网频率偏差；ΔPg(s)为火电机组出力；部分参数参考文献[30]，TG、TCH、TRH分别为火电机组调速器时间常数、汽轮机时间常数、再热器时间常数，其取值分别为0.08 s、0.3 s、10 s；Tb为储能电池的时间常数，取值为0.1 s；FHP为再热器增益，取值为0.5；无渗透率时M对应的值为5，D取值为1；s为拉普拉斯算子(以上取值均以对应最大容量为基准的标幺值)。从负荷扰动与电网频率之间的特性展开研究。

图2 计及新能源渗透率的区域电网调频模型Fig.2 Frequency modulation model of powersystem with new energy penetration

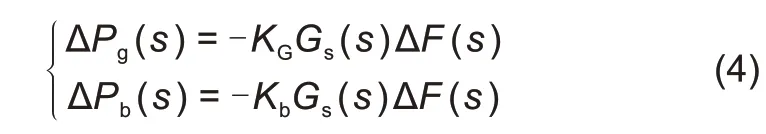
ΔPg(s)+ ΔPb(s) - ΔPL(s)=(M's+D)ΔF(s) (5)

式中，ΔPL(s)为负荷扰动；Gb(s)为储能电池的一阶惯性模型；Gs(s)为火电机组的汽轮机模型，其传递函数分别为

负荷扰动与电网频率偏差之间的数学关系式为

含储能时频率偏差与负荷扰动的幅频特性函数为

不含储能时频率偏差与负荷扰动的幅频特性函数为

当Kb标幺值为24，KG标幺值为20时。根据不同的渗透率以及是否有储能的加入，得到四种情况下的区域电网频率特性函数，并采用伯德图分析其幅频特性，如图3 所示。存在p= 20%以及p=10%两种情况；在相同的负荷扰动条件下，由图3可知：在没有储能加入的情况下，加入新能源时，其幅值比没有新能源加入时高，表明新能源的加入降低了系统的频率稳定性；在f＜0.2 Hz 频段，在有新能源的基础上时加入储能，其幅值远远低于无储能有新能源的情况，表明储能对电网的频率稳定具有支撑作用；在0 Hz ＜f＜10 Hz 和45 Hz ＜f＜60 Hz频段，渗透率为10%时储能调频幅值低于渗透率为20%时调频的幅值，表明储能系统主要作用于此频段，且能很好地抑制新能源的扰动以及负荷扰动带来的影响，降低了电力系统频率波动和最大频率偏差。

图3 区域电网幅频特性曲线Fig.3 Amplitude frequency characteristic curves of regional power grid

2 调频用储能电池的无模型自适应控制策略

2.1 基本原理

以一个单输入单输出(SISO)的受控系统为例，图4 中x代表系统整体的输入量，u表示控制器的实际输出量也为受控系统的输入，y为受控系统的实际输出量。受控系统的输出与输入量之间的关系可以描述为y=f(u)，其中f(u)是受控系统的数学模型。通常情况下，由于受控系统内部组成部分多且复杂，难以建立受控对象较准确的模型。这使得基于受控对象精确数学模型的控制方法的应用得到限制，达不到控制效果，此时就可利用MFAC控制方法来解决这个难题，用泛模型来代替这些未知或者不够精确的模型。

图4 SlSO控制系统Fig.4 Single input single output control system

它使用的是一种新的动态性新化方法及伪偏导数法，利用受控系统的输入输出数据，就可得到系统每个工作点的动态线化数据模型，所有数据模型组成为泛模型，当被控系统发生改变时，通过伪偏导数算法可以将这些改变的信息传递给线性数据模型，使泛模型也作出调整。然后对此泛模型进行求解控制，控制问题转化为在已知泛模型期望输出以及其数据模型，求解一个值使泛模型能得到这个期望，将这个求得的值作为被控系统输入，就可以使被控系统得到期望的输出。

2.2 无模型控制框图

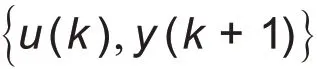
式(12)为控制律算法，其中，l[l∈(0,2)]是学习因子，p是一个权重因子，p的作用是对u(k)的值做一个限制以及保证式(12)的分母不为零。

图5 MFAC算法实现框图Fig.5 lmplementation block diagram of MFAC algorithm

2.3 针对储能电池的无模型控制器设计

结合储能电池荷电状态经济安全运行范围、储能电池数学模型难以精确以及满足电网调频需求等条件，提出考虑储能电池SOC，基于储能系统输入输出数据驱动的无模型自适应控制策略。

本文的被控系统为储能电池，它的输入数据为电网的频率波动ΔF(s)和荷电状态(QSOC)，根据两者进行出力调整，即ΔPb(s)为被控系统的输出，达到对电网频率的支撑效果，针对此储能电池，可以将无模型控制器设计为一个两输入一输出(MISO)的控制系统，将电网的实时频率偏差和QSOC作为无模型控制器的输入(两输入)，经过无模型自适应控制器之后得到修正后的频率偏差值(一输出)，从而调整储能的出力ΔPb(s)，利用前面提到的无模型控制器构建方法，对储能电池参与电网调频进行控制。

数字X线引导下下肢静脉造影不仅具有X线定位准确、图像清晰度高的优点，且能实时数字化获取数据，录像后可利用图像后处理软件多角度分析检查结果[11-13]，但由于对反流程度无法进行定量分析、且属于有创性检查，因此，在临床中并未作为首选检查方法。彩色多普勒超声检查是常用的下肢静脉疾病诊断检查方法[14-16]。彩色多普勒血流显像模式具有无创、动态显示血流动力、直接测量反流程度的优点，但其对深静脉瓣膜结构无法高清显示，且检查准确性易受检查者水平影响，因此，其虽然是临床首选的诊断检查方法，但对于部分深静脉病变仍需进一步行数字X线引导下下肢静脉造影检查。

基于MFAC的储能电池调频控制系统原理图见图6，MFAC 控制器的内部结构可以根据式(11)、式(12)以及图5 设计得到。电池荷电状态健康的允许范围为0.2～0.8，同时为避免储能出力超过自身调节能力范围，应设置出力限幅环节。

2.4 电池储能参与一次调频的评价指标

为评估所提无模型自适应控制策略的有效性，考虑发生阶跃负荷扰动以及连续负荷小扰动两种工况，并由此分别提出两类评价指标。

若负荷为阶跃扰动，评价调频特性的指标主要有最大频率偏差|Δfm|、最小频率偏差|Δfs|以及分别对应的时刻ts和tm，同时定义频率恢复期间的恢复速度β，β=(|Δfm|-|Δfs|)/(ts-tm)，以及频率跌落时的下滑速度α，α=|Δfm|/tm。

由上文可知，在阶跃负荷扰动时，|Δfm|和|Δfs|越小证明调频效果越好，α越小表明抗干扰能力强，β越大证明调频响应速度越快。

如果负荷为连续扰动，则以频率和QSOC偏离各自基准值作为评价指标，反映其与期望值的离散程度：

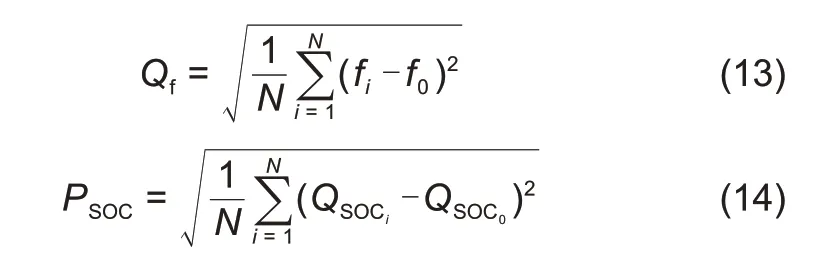
式中，Qf、PSOC分别为频率指标和QSOC指标；f0为电网额定频率50 Hz；QSOC0取值0.5。Qf越小频率越稳定、PSOC越小，电池容量保持效果越佳。

3 仿真分析

3.1 仿真模型

在Matlab/Simulink中搭建了与图6对应的调频仿真模型，参数(部分参数已在图6 介绍中给出)均为标幺化后的值，本文所提储能控制策略搭建根据式(11)、式(12)和图5。最大火电机组额定容量为100 MW，电池储能系统容量为1 MW/1 MWh[30]。

图6 基于MFAC的储能电池调频控制系统原理图Fig.6 Schematic diagram of frequency modulation control system of energy storage battery based on MFAC

3.2 仿真工况及仿真类型

为验证无模型自适应策略的可行性，根据上文提出的调频指标，即需要仿真系统在阶跃负荷扰动和连续负荷扰动两种工况下的表现。对于储能调频出力控制环节，使用四种不同的控制方法：储能不参与调频；传统定下垂控制策略；采用参考文献[30]所提基于QSOC的变下垂自适应综合控制策略(简单型)；采用本文计及QSOC基于数据驱动的无模型自适应控制策略。其中，第二种和第三种控制策略下文分别称为定K法、变K法。

3.3 阶跃负荷扰动仿真分析

在仿真系统中加入大小为0.08(标幺值)的阶跃负荷扰动，并对4种策略参与调频的特性进行仿真分析。当初始QSOC为0.5时在该扰动下的系统频率偏差曲线如图7 所示，QSOC变化曲线如图8 所示，初始QSOC为0.5 的调频评价指标见表1。在更低的初始QSOC为0.3情况下对各方法进行仿真，结果如图9、图10所示。

图7 初始QSOC=0.5下阶跃负荷扰动频率偏差曲线Fig.7 Step load disturbance frequency deviation curves when QSOC=0.5

图8 QSOC=0.5时QSOC变化曲线Fig.8 Change curves of QSOCwhen QSOC=0.5

图9 初始QSOC=0.3下阶跃负荷扰动频率偏差曲线Fig.9 Step load disturbance frequency deviation curves when QSOC=0.3

图10 初始QSOC=0.3时QSOC变化曲线Fig.10 Change curves of QSOC when QSOC=0.3

由图7 以及表1 可知，扰动开始时，4 种调频策略的系统频率均急速降低，系统无储能参与时频率跌落最多且下降速率较高；有储能参与的3种策略频率下降都较小，其中定K法和无模型控制策略最小；在频率恢复阶段，无模型自适应控制方法能将频率偏差稳定在一个较低的范围内，且恢复速率较高。本文策略兼顾QSOC保持效果，调频效果与定K法差异不大。但对比不同初始QSOC情况下的QSOC变化曲线，可知在初始QSOC值较低时，定K法会因较快耗尽能量而使储能早早退出调频，使系统频率再次跌落冲击电网，且冲击会影响电池使用寿命。结合以上，在阶跃负荷扰动时，变K法和本文方法的调频指标效果均较佳，但本文方法的QSOC保持效果指标最好。

表1 初始QSOC=0.5下的调频评价指标Table 1 Frequency modulation evaluation index When QSOC=0.5

3.4 连续负荷扰动仿真分析

仿真对比连续扰动负荷(短时和长时)下上述4 种策略参与调频的特性。在仿真系统中加入连续负荷扰动如图11所示，并对各方法进行仿真。

图11 5 min连续负荷扰动曲线Fig.11 Five minute continuous load disturbance curves

首先仿真对比4 种方法在5 min 短时连续负荷扰动下的调频特性。图12 为频率偏差曲线，图13为QSOC变化曲线，表2 为该扰动下各项评价指标。观察结果可知，没有储能参与时系统频率波动最大；本文方法和定K法的频率偏差曲线大致相同，且都将值维持在一个较小范围内，但QSOC保持效果指标均比变K法差。短时连续负荷扰动时追求的是能够快速提供频率支撑，应把调频效果放在首要位置，因此短时扰动时使用定K法和无模型自适应控制方法参与调频都是可行的。

表2 5 min连续负荷扰动评价指标Table 2 Evaluation index of five minute continuous load disturbance

图12 5 min连续扰动下频率偏差曲线Fig.12 Frequency deviation curves under five minute continuous disturbance

图13 5 min连续扰动下QSOC变化曲线Fig.13 Deviation curves of QSOC under five minute continuous disturbance

进一步仿真对比4 种方法在1 h 长时连续负荷扰动下的调频特性，图14 为频率偏差曲线，图15为QSOC变化曲线，表3 为评价指标。分析结果可知，有储能参与时的三种控制策略在调频初期均将频率偏差维持在一个较小的波动范围内，变K法的波动略大；随着持续放电，三种方法的频率偏差波动范围均在加大，但定K法因一直使电池出力在一个较大的值，导致电池能量较早耗尽造成频率的再次跌落；本文方法QSOC的保持效果指标最佳，总体看来另外两种方法效果较差；在长时连续扰动下应首先考虑电池的QSOC保持效果，因此无模型自适应控制策略的优势更明显。

图14 1 h连续扰动下频率偏差曲线Fig.14 Frequency deviation curves under 1-hour continuous disturbance

图15 1 h连续扰动下QSOC变化曲线Fig.15 Deviation curves of QSOC under 1-hour continuous disturbance

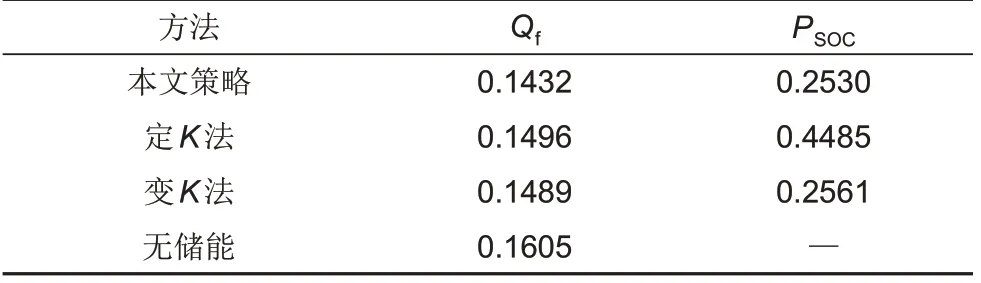
表3 1 h连续负荷扰动评价指标Table 3 Evaluation index of 1-hour continuous load disturbance

综合以上分析可知，本文提出的无模型自适应控制策略在短时连续负荷扰动与定K法在调频效果指标上均较优；长时负荷扰动时，本文方法QSOC保持效果指标最佳。不论短时、长时连续负荷扰动本文方法均具有可行性，凸显一定的自适应性。

4 结 论

（1）建立并分析含储能的高渗透率区域电网调频模型，有储能参与调频时，区域电网幅频特性函数模值小于无储能的情况，表明储能的加入能提高系统的抗干扰能力。

（2）利用无模型自适应控制策略将系统频率与QSOC作为控制器的驱动数据动态调整储能出力，在维持电池健康经济性的同时最大限度地让储能参与到调频。在阶跃负荷扰动下，在较高初始QSOC时，频率偏差值都较小，本文调频效果与其他控制策略差别不大，但在较低初始QSOC值时，本文频率偏差值最小，调频效果显著，且QSOC评价指标值最小，QSOC保持效果最佳；在长时连续扰动下本文的QSOC评价指标值最小，QSOC保持效果最优，总体调频效果优于其他控制策略。

（3）伴随着各种新能源的并网带来的系统内部结构复杂化，很难建立精确的系统数学模型，通过无模型自适应控制可减少对储能系统的数学模型的依赖，本文只使用储能系统的输入输出数据作驱动进行控制设计，能动态调整模型的参数，控制效果自适应度高。