基于双向长短时记忆网络和设备未来态的停电优化模型

薛 斌 ，马晓伟 ，任景 ，郭少青 ，黄红伟 ，薛艳军

(1.国网电网有限公司西北分部,陕西 西安 710048；2.北京清大科越股份有限公司,北京 100102)

在特高压远距离直流输电以及能源互联网的建设发展下,电网规模日益增大,形成了多能源互联和远距离输电的格局,在多源、互补、互联的复杂大电网中,因为检修和事故等原因导致的电力系统停电对需求侧用户和电力系统安全运行都会产生重大的影响,因此准确计算电力系统的停电损失并用于指导电力系统的安全调度和控制是当前电力系统的核心,已经引起了国内外专家学者和国家电网公司的高度重视[1-3]。

针对电力系统停电领域的研究主要包含停电检修计划、停电风险建模、停电事故分析及黑启动等方面,例如文献[4-5]从停电损失和经济成本方面进行建模,建立了损失评估模型。文献[6-8]从停电导致的电力系统稳定性改变方面建立了电力系统停电风险和损失模型。文献[9-11]从电网检修安全经济的角度,提出了输电网检修计划、发输配检修计划的编制方法。文献[12-15]研究了电力系统停电对各个方面的影响,采用主观和客观打分法建立了停电对电力系统的综合影响评估模型。文献[16-19]针对配电网中的设备健康状态,提出了设备故障率的停电概率评估模型。

虽然目前在电力系统停电计划、检修安全风险和经济方面提出较多的优秀方案,但没有考虑停电范围及其电网拓扑结构对电网安全运行存在的隐患。对此,从时间维度、空间维度、元器件维度提出了设备多维度未来态及其关联停电拓扑的停电优化模型,基于双向长短时记忆网络的优化算法智能优化制定未来发输变的停电计划。

1 电气设备时间维的健康评估

电力系统设备主要考虑电缆线路、断路器、隔离开关、高低压负荷开关、变压器及其配件等设备,通常来说,随着设备使用时间的延长,其故障率负荷浴盆曲线[20]通常与设备的运行年限有关,如图1 所示。图1 中横坐标t表示设备运行时间,纵坐标λ(t)表示设备的故障率。

图1 电气设备的浴盆曲线

由图1 可见,电气设备浴盆曲线通常具有三个阶段,第I 阶段是设备出厂运行的初期,是环境、操作的磨合期,故障率逐渐下降；第II 阶段主要是设备运行的正常状态,此时故障率较低；第III 阶段是随着设备运行时间的增长,设备老化、环境因素、操作情况等导致的故障率逐渐增大。因此,需要从时间维度上分别对设备的健康状态建模。

通过实践证明,威布尔分布可以较好地拟合图1所示的浴盆分布曲线,因此电气设备的故障率通常都使用该分布函数予以表达:

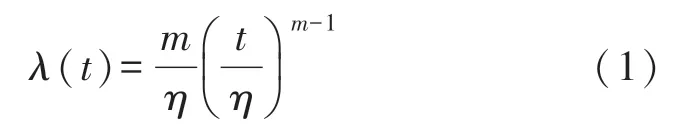
式中:t表示时间；λ(t)表示电气设备随时间变化的故障率；m表示威布尔分布的形状结构；η表示威布尔分布的尺度结构。

针对图1 中不同阶段的电气设备运行数据,融入威布尔分布函数式(1)中,可以得到式(1)中的参数m和η。

在实际运行过程中会因为环境影响、人为因素、设备老化、家族缺陷等诱因,导致式(1)中的分布有所偏差,因此需要对于一些特殊情况进行校正。

首先,对于用电高峰的过载负荷时刻,式(1)中的参数就要进行校正,因为过载负荷对于设备停电具有直接影响,设负荷过载量表示为:

式中:PL表示电气设备的负载率；PLr表示负载率的额定值。

当获得了电气设备的负载率后,可以用指数模型来表示其状态:

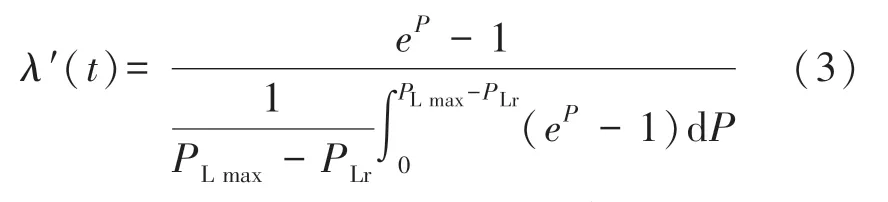
式中:λ′(t)表示此时的电气设备健康状态评估值；PLmax表示负载率的最大值；P表示式(2)中的过载量。

其次,在电气设备运行过程中,强降雨、雷暴、强风天气也会导致停电,此时的电气设备故障率模型可以表达为λ″(t):

式中:M表示电气设备运行天数；Nm表示电气设备运行的第m天中强降雨、雷击、风暴累计小时数；Ni表示电气设备运行的第i天中强降雨、雷击、风暴累计小时数。

得到电气设备的故障率后,可以获得电气设备健康程度:

式中:A和B表示模型的参数；λ表示故障率；H表示健康值。

以某地区电气设备的实际运行数据代入上述模型,可以计算得到参数A和B。

2 元器件关联的停电拓扑模型

对于某一电气设备停电将引起与之关联的多个变压器、输电线路、高低压开关等停运(通常来说,多发生在配电网)。

针对尚未停电的电网区域来说,将停运电气设备与变电站、输电线路、高低压开关、需求侧用户、智能电表等设备形成关联区域,由于停运会造成电压算法相似性和一致性,因此采用Tanimoto 相似度算法[21]予以识别。

设两个关联的电压节点为Pa和Pb,该两个节点随着时间变化的历史电压可以分别表示为:

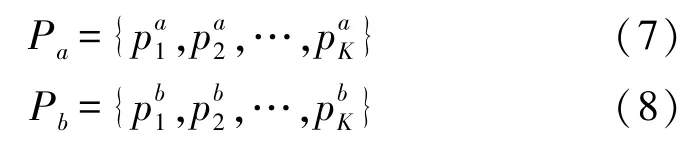
式中:K表示序列数量,为一个较大的正整数；表示在时刻1 时电压值占整个序列的比例,以此类推,具有相同的含义。

为了表述的一般性,设式(7)和式(8)中的序列总数量分别为m和n,用状态量Fa和Fb分别表示上述两个集合,那么式(7)和式(8)可以分别表示为:

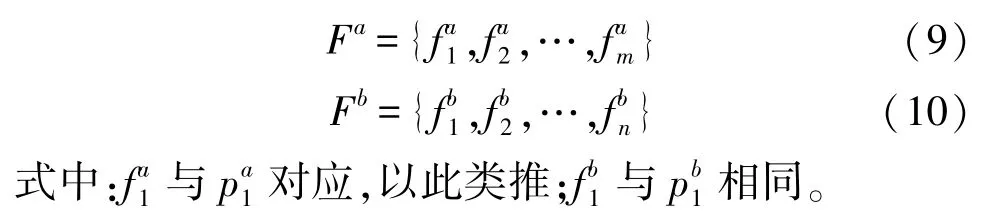
依次对式(9)和式(10)进行均值化计算:

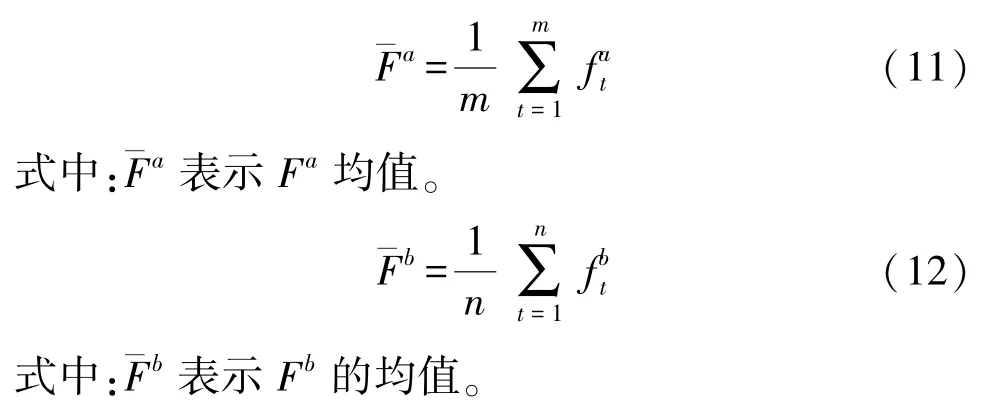
根据Tanimoto 原理,两个具有一定关联的节点之间的电压相关度可以计算为:

经过上式计算,可得二者之间的相关度为:

对于式(14)中的计算结果:

当式(15)中的计算结果越接近1 时,说明关联的两个节点相关度越高,发生停电的几率越大,因此可以设置一个阈值(如0.8),当超过阈值后,可以认为同时处于停电区域。

3 安全经济的停电模型

传统电力系统停电过程中没有考虑供电企业或者用户,且不同用户的经济损失不同,对此本文从发电企业、不同用户不同时间段的整体考虑停电影响的经济性和可靠性。

3.1 停电用户经济损失模型

用户停电的经济损失由停电时间长短可以直接计算得到:

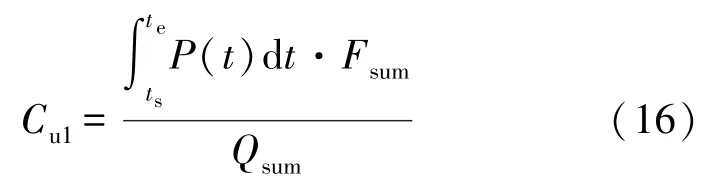
式中:Cu1表示用户停电的经济损失；ts表示停电的开始时间；te表示停电的结束时间；P(t)表示用户随时间变化的负荷值；Fsum表示停电区域的总经济收入；Qsum表示停电区域的总停电量。

式(16)是计算用户的直接经济损失,但是还存在隐含的关联经济损失,例如用户在生产某种产品时因为上下游停电导致某个零部件无法供应或者质量缺陷,由此造成经济损失。由此需要定义一个用户经济损失的关联影响系数:

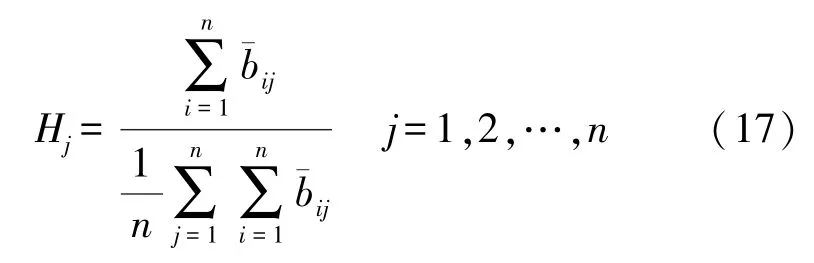
式中:n表示关联影响系数矩阵的维数；表示系数矩阵第j列元素之和；表示系数矩阵所有列元素的均值；Hj表示第j个部门增加一个产品零部件对其上下游产品行业的供需经济拉动程度；表示上下游产品与关联产品之间的关联程度。

通过式(16)～式(17),可以得到停电用户的总经济损失模型为:

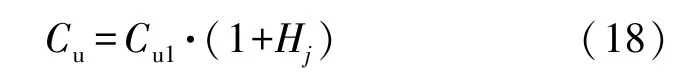
3.2 电力企业经济损失模型

大规模停电对于电力企业来说,主要经济损失是电费收入、设备维护费用,计算方式为:

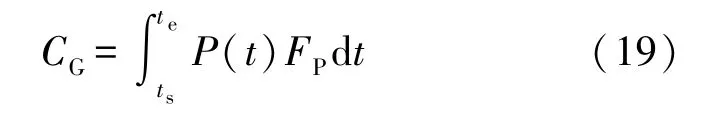
式中:CG表示在一次停电过程中电力企业的经济损失；FP表示电力企业发布的峰谷电价,表示为:

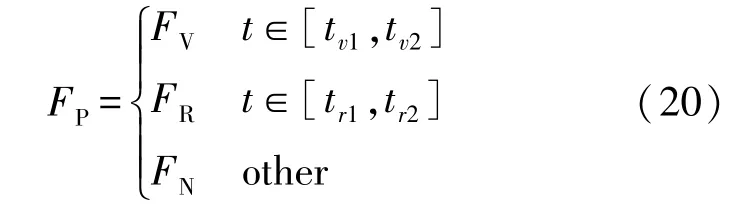
式中:FV表示谷电价；[tv1,tv2]表示谷电价所在的时间段内；FR表示峰电价；[tr1,tr2]表示峰值电价所在的时间段内；FN表示平电价。

3.3 电力企业供电可靠性模型

电力企业供电可靠性是保证电力系统安全运行的基础,电力企业供电可靠性指标可以使用如下模型:

式中:TAIHC表示电力系统的平均停电时间；Ttotal表示电力系统中的所有地区总停电时间；Mtotal表示电力系统中停电地区的总数。

在式(21)的基础上,可以定义电气企业供电可靠度RRS的指标:

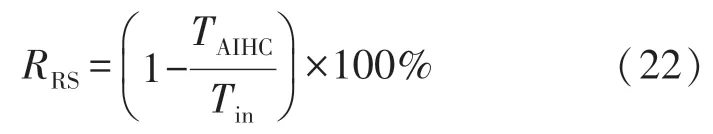
式中:Tin表示计算过程中的设定时间。

3.4 可靠性和经济性的停电模型

根据上述可靠性和经济性模型,并计及未来网络状态,建立优化模型为:

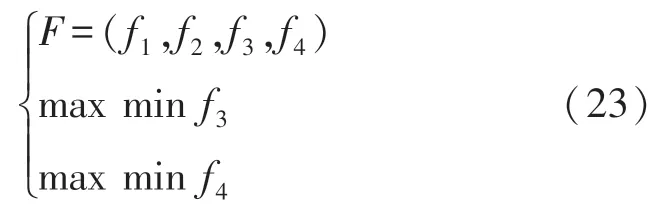
式中:f1表示电气设备的健康模型；f2表示电气设备关联的电网停电拓扑模型；f3表示经济性模型；f4表示可靠性模型。

3.5 基于粒子群的停电优化求解

对于式(23)中的优化模型,需要计算停电损失的最小值和停电可靠性的最大值,粒子群优化能够求解上述的最小和最大值问题,因此使用粒子群优化函数分别对式(23)的最小值、最大值分别进行求解。

设粒子群的种族规模为m,决策量为n,初始化粒子群中的速度和位置为符合高斯分布的随机函数。

设在优化过程中的t时刻,第i个粒子的速度为:

同时,在该时刻,该粒子所处于的位置为:

根据粒子群交互方式可得,在t＋1 时刻的速度和位置为:

式中:ω表示粒子运行过程中的权值；c1和c2表示粒子交互过程的学习系数；r1和r2表示服从高斯随机分布的随机数；vmax和vmin表示粒子运行过程中的速度上限和下限；分别表示式(25)中的粒子位置。

4 双向长短期记忆网络求解

3.5 节的粒子群优化算法主要针对现在状态求解最大值、最小值模型,无法对于外来电网停电模型进行预测和计算。对此,使用深度学习理论的双向长短期记忆网络方法予以实现。

4.1 双向长短期记忆网络

双向长短时记忆网络(Bi-directional Long Short-Term Memory,BLSTM)是在LSTM 基础上发展而来的,它有前向和后向两个相互交叉迭代的训练过程,摒除了传统梯度下降陷入局部最小的缺陷,改进了传统LSTM 只能前向学习训练过程。

BLSTM 通过前向训练,学习输入数据在顺序时间过程存在的关联性；通过后向学习,加入未来输入数据,挖掘反馈之间的关联性。通过前向、后向学习,加入未来数据,能够提高LSTM 的精度。

传统的LSTM 结构如图2 所示,其包含输入门xt、遗忘门ft、输出门Ct等构成。

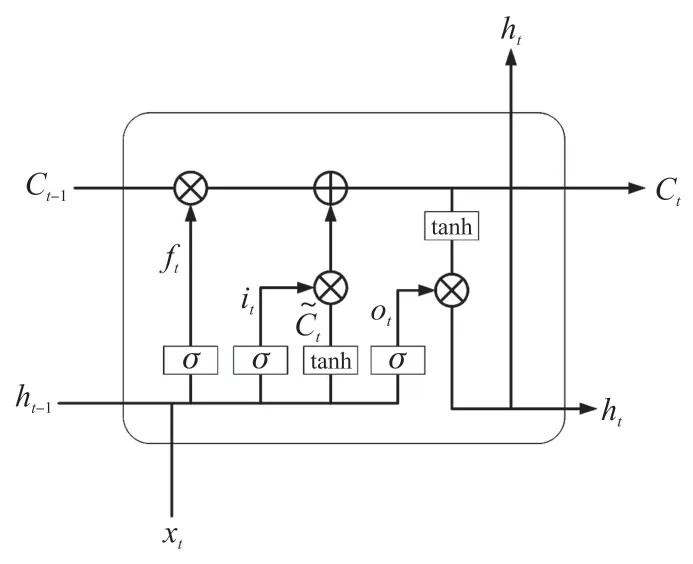
图2 LSTM 结构图

其工作原理为:

首先遗忘门的输出为当前输入xt、前一时刻隐含信息ht-1作为输入,经过作用函数σ的计算后得到:

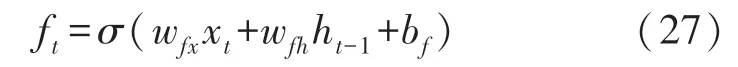
式中:wfx、wfh为需要训练的权值；bf为扰动量。

由图2 可见,it对输入的数据进行加工筛选,从而减少计算维度:

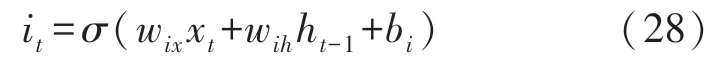
式中:wix、wih也为需要训练的权值；bi为随机量。

经过式(27)和式(28)的计算,可以得到更新的信息:

式中:wcx和wch为需要训练的权值；bc为随机量。

经过更新以及LSTM 原有的积累,可以得到t时刻LSTM 计算值:

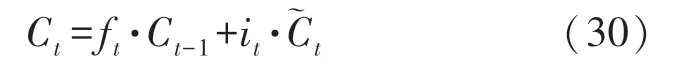
根据图2 进而可以得到当前输出值:

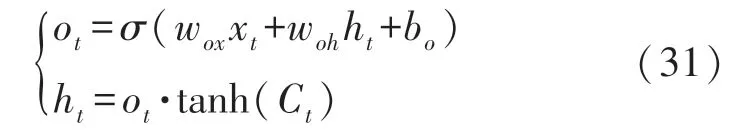
式中:wox、wah表示权系数,bo表示偏置量。

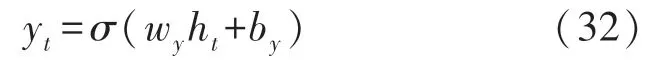
式中:wy为需要训练的权值；by为随机量。

由上述可见,LSTM 能够解决历史数据学习功能,但是没有充分利用未来的信息,比如未来负荷预测,因此采用BLSTM 能够解决该问题。

BLSTM 是在LSTM 结构的基础上,添加了前、后两个时间序列相反的隐含层；然后将其连接到一个输出,前向的隐含层为式(32),后向的隐含层为:

式中:ft＋1表示t＋1 时刻由式(27)获得的计算结果；it＋1表示t＋1 时刻由式(28)获得的计算结果。

BLSTM 的网络结构如图3 所示。

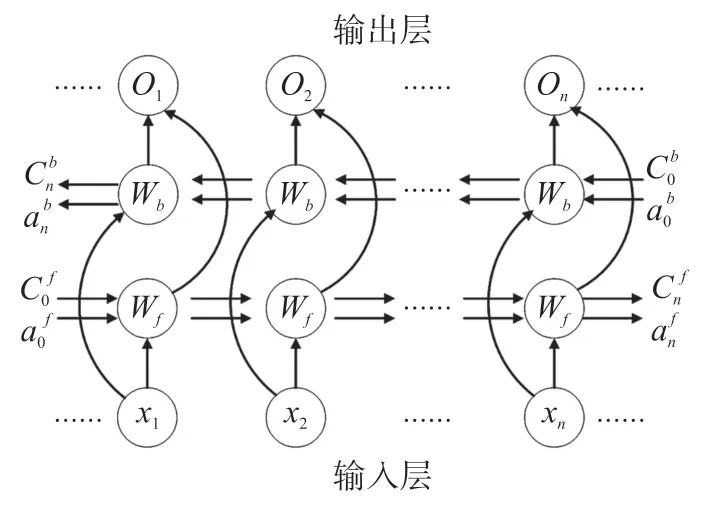
图3 BLSTM 结构图

4.2 双向长短期记忆网络求解

按照时间的由远及近,可以获得电力系统的多种场景下的潮流,该潮流是以某一地区电气设备的投运、老化、故障及停运的时间过程为基础实施的。

在此基础上,按照第3 部分予以求解获得电力系统停电的经济性和可靠性数据,将其按照时间前后作为BLSTM 的输入:

将式(34)中的输入数据按照3.5 节的方法进行求解,结果作为BLSTM 的输出训练其权值,用来未来电网停电的预测和计算。

将电气设备未来一段时间,如t＝T(T＞n)的f1,f2,f3,f4作为BLSTM 的输入,从而可以预测得到该时刻下的停电情况。

5 算例分析

采用如图4 所示的某地区实际电网为例,验证本文所提出的算法。该地区电网包含2 台发电机、8个负荷、13 条输电线路、10 台变压器、2 台断路器、1个隔离开关、16 个负荷开关构成。

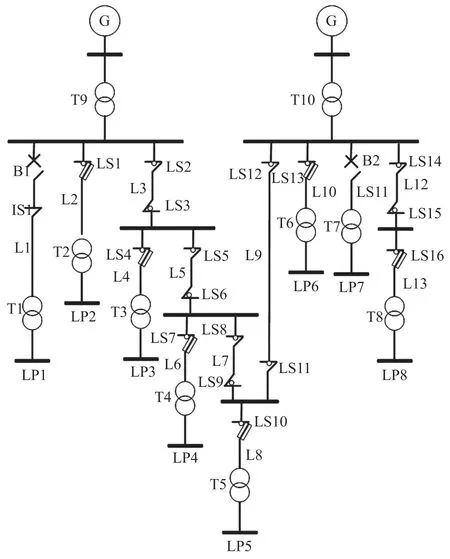
图4 某实际电网结构

为了实现上述算法,在Windows 下使用Python和MATLAB 编写上述算法。

对于图4 中的输电线路,其参数如表1 所示。

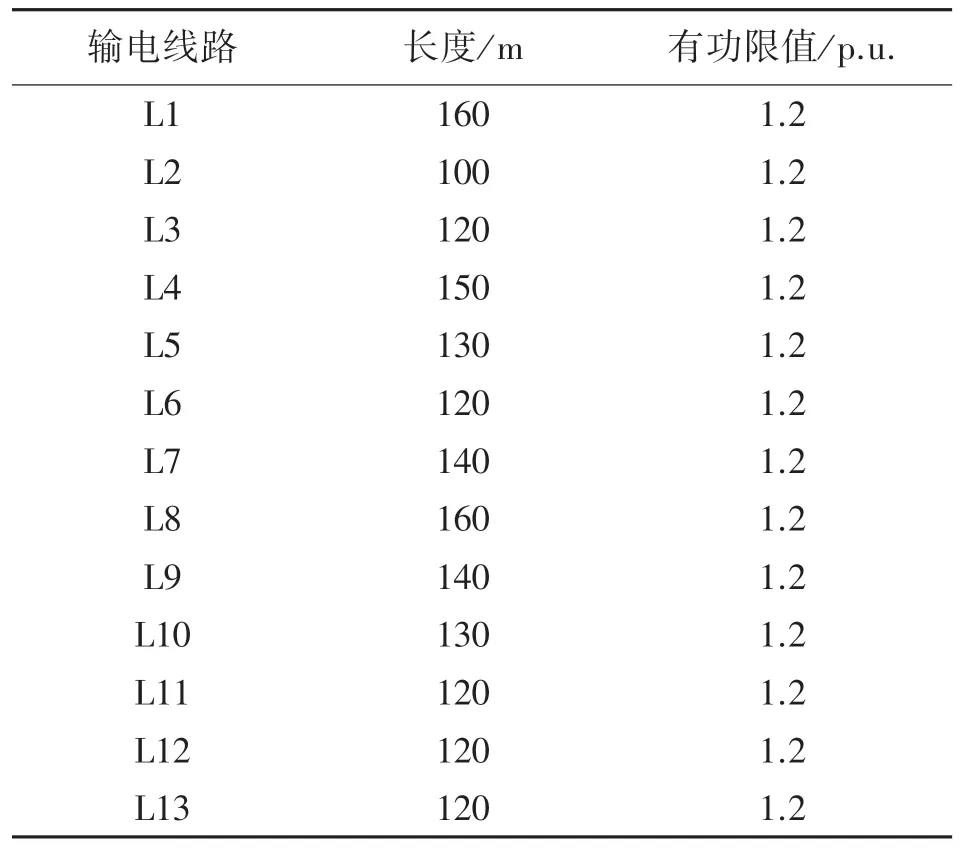
表1 输电线路参数

对图4 所示地区2015 年至2017 年电气设备的老化情况、雷电和风暴情况,进行故障率修正模型的计算,可得表2 所示的故障率。

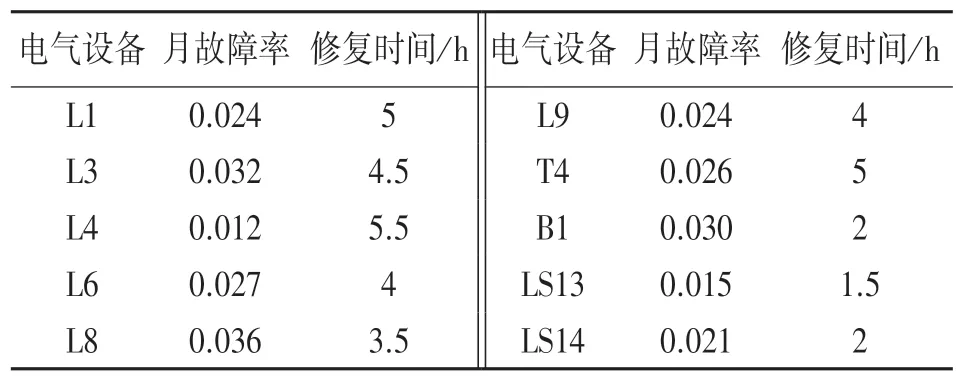
表2 电气设备故障率

将电气设备的故障率代入健康指标中,可得各个设备的健康指数,如表3 所示。

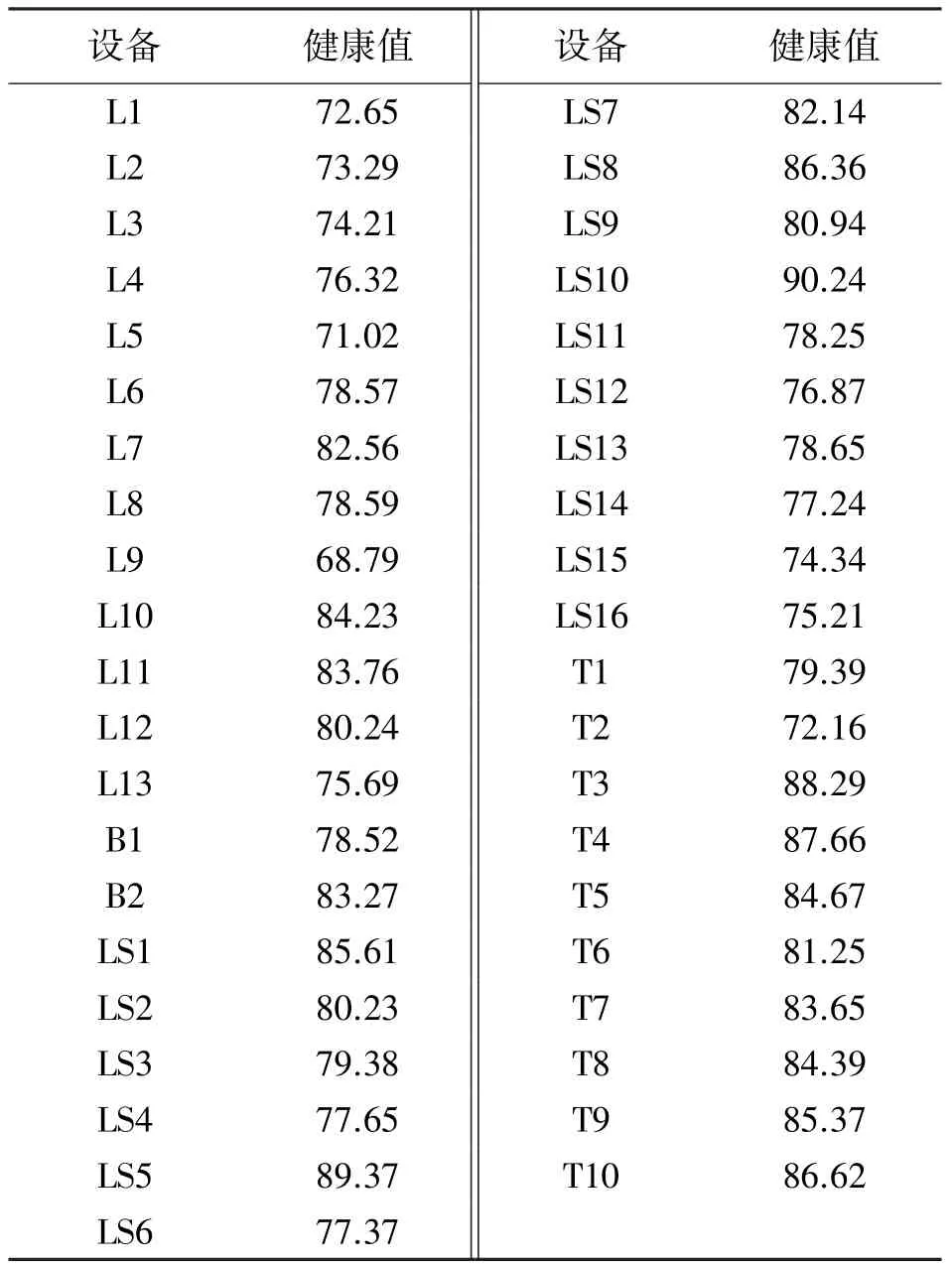
表3 电气设备健康指数

对于电气设备停电造成的关联电网拓扑,按照Tanimoto 原理[21],假设T9 变压器故障,可以得到关联的拓扑电网结构元器件如表4 所示。

表4 电气设备的相关度

假设变压器T9、T10 发生故障导致相关电网停电,按照第3 部分的计算模型可以获得相关的经济性、可靠性计算结果如表5 所示。

由表5 可见,对于变压器T9 故障导致的电网停电,将使负荷LP1、LP2、LP3、LP4 和LP5 停电,产生较大的经济性影响；变压器T10 故障导致的电网停电,将使负荷LP6、LP7 和LP8 停电,由此造成较大的经济损失。

表5 停电经济性、可靠性结果

将T9 故障和T10 故障的多种场景作为训练集合,相应的经济性和可靠性作为输出代入BLSTM 进行训练,用于对未来某种故障导致的电网停运所造成的经济损失的计算,可得表6 所示的结果。

表6 T9 和T10 故障导致的电网停电结果

表6 中的训练集1、训练集2、训练集3 分别使用的是2015 年中采集的100 例故障样本集、2015年～2016 年采集的200 例故障样本集、2015～2017年采集的300 例故障样本集的运行数据集合。通过表6 的运行结果可见,随着训练样本的增大,训练结果的精度逐步增大,但增大的不明显,因为在训练集中电气设备关联的各种设备状态组合没有完全涵盖所有场景。可以预见,若训练集中的场景足够多,那么就可以进一步提高预测的准确度。

6 结论

针对电气设备停运导致的停电经济性、可靠性问题,在考虑了电气设备自身老化、暴雨、强风影响下的故障率模型基础上,计及关联设备拓扑结构,并给出了相应的经济性和可靠性模型,基于BLSTM 训练模型给出了电网的停电优化计算方法。通过实际电网的仿真验证,可得如下结论:

(1)电气设备的老化计算、强风和暴雨对于电气设备的故障率具有一定的影响。

(2)考虑停电设备关联拓扑的经济性和可靠性模型具有较高的实际意义。

(3)基于BLSTM 对于故障场景的训练能够准确地预测和计算结果。