基于自适应神经模糊推理系统的智能电表大数据分析研究

王登峰，李英，杨琦，马广霞，樊博

(国网宁夏电力有限公司电力科学研究院,宁夏 银川 750011)

智能电表是应用于智能电网和用户之间双向通信的重要设备,具有高时间分辨率数据采集(通常每秒钟或几分钟)和长时间运行的优点,但随着数据的累积从海量数据中检索有用信息的难度日益增加,因此智能电表数据分析(MDA)已经成为智能电网研究领域的重要研究方向之一[1-3]。

基于智能电表大数据实现负荷预测是电网智能化的重要体现,电网运行单位可以根据负荷预测控制大功率热负荷和冷负荷的交替运行以保证电网的可靠性。为解决负荷预测问题,自90 年代起就有许多学者进行了探索[4]。其中软计算技术在负荷预测方面获得了成功应用,例如人工神经网络(Artificial Neural Network,ANN)[5-8]、神经模糊法[9]和模糊逻辑[10]、时间序列分析[11]、支持向量回归(Support Vector Regression,SVR)[12]等等。然而由于设备的限制,早期的大多数研究工作无法获取用电户的高时间分辨率电力消耗数据,使得预测模型精度不佳,预测能力受到较大限制。

为此本文从用电住宅楼采集了大容量、高时间分辨率的智能电表数据用于负荷预测,基于自适应神经模糊推理系统(Adaptive Neural Fussy Interence System,ANFIS)混合软计算技术建立了负荷预测模型,利用智能电表数据进行了预测模型构建、训练和测试,最后对用电户在24 h 内各个时间的电力功耗进行了预测,并利用实际数据集进行了对比验证。研究结果可为高时间分辨率的电力负荷预测提供参考。

1 模糊系统模型

人工神经网络和模糊系统是软计算方法中的两个重要组成部分[13-15],人工神经网络和模糊系统是两个互补的概念:人工神经网络具有从数据中学习的能力,而模糊系统则是基于特定规则的数学模型。目前模糊逻辑已得到各种应用,并且在研究界受到广泛关注,由于模糊系统本身不具备学习能力,因此必须从其他技术中借鉴这一能力。整合人工神经网络和模糊系统的混合计算技术即自适应神经模糊推理系统[16]。ANFIS 具有学习和推理能力,从而提高了模型的预测准确性。本文基于ANFIS 系统建立数学模型,模型主要有以下几个部分组成。

1.1 模糊集模型

模糊逻辑的理论基础是模糊集理论,其中变量由一个或多个集的成员组成,该变量集的关系通过隶属函数进行定义[17]。与经典集合理论不同,模糊逻辑模型中允许使用的值是单词而不是数字,因此人们可以用单词进行计算。尽管单词本质上不如数字精确,但是单词计算可利用容差,该容差更接近于人类的推理过程。

模糊集是一类连续隶属关系对象,这样的集合通过隶属度函数(MF)进行描述,隶属度函数为每个对象分配介于0 到1 之间的隶属度等级[18],通过隶属度等级确定元素是在集合中(取值为1)、不在集合中(取值为0)、或者部分在集合中(取自位于0～1 之间)。从形式上看X范围内的模糊集A定义为:

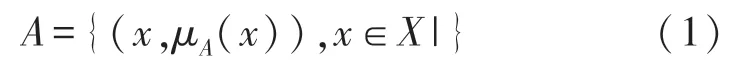
式中:μA(x)是x和其隶属度函数A的函数名。

1.2 隶属度函数

模糊系统的核心是一组隶属度函数,这些函数定义了模糊语言变量的边界,隶属度函数定义的平滑边界范围位于0～1 之间,而不是清晰的逻辑边界。目前有多种可选用的隶属函数,可根据问题要求从中选择,在可用的几种隶属函数类型中,最常用的隶属函数是三角形隶属函数和梯形隶属函数,在ANFIS 网络中通常使用高斯隶属函数,其定义公式为:

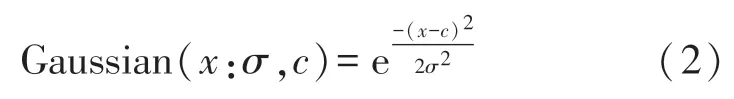
式中:σ是标准差,c是均值；Gaussian 代表高斯函数名。

1.3 模糊系统的if-then 规则

模糊推理系统的规则基础是将一组输入要素与输出相关联的if-then 规则。模糊推理规则的形式为:

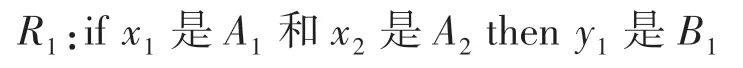
式中:xi是Ai的前提条件；yi是Bi的结果或结论,本文将一组这样的模糊if-then 规则用于构建称为知识库的模糊推理系统(FIS)。

1.4 模糊推理系统模型

使用模糊逻辑建立输入-输出映射的过程称为模糊推理,模糊推理系统在称为知识库的模糊规则集合的基础上工作。这些规则的制定对于模糊推理系统非常重要,在大多数情况下,推理系统需要有关具体问题的必要知识。因此通常采用将人类专家的经验移植到模糊规则制定的办法,经验移植过程需要进行多次试验才能最终得出一组具体的模糊规则,但是在没有专家的情况下,如果使用一组观察值(先验知识),仍然可以对模糊系统进行建模。这些观察结果(先验知识)主要用于训练ANFIS 网络,ANFIS 从输入系统的观察结果中了解系统的行为,再制定模糊规则以及调整相关隶属函数的参数,从而进一步构建出模糊推理系统。

1.5 ANFIS 系统结构

本文提出的ANFIS 是如图1 所示的多层神经网络。系统由五层结构组成,第1 层具有适用于输入数据的自适应节点；第2 层具有固定节点,其输出确定了规则强度；第3 层中有固定的节点,用于计算归一化的规则强度；第4 层具有自适应节点,可计算后续参数；第5 层仅有一个节点,该节点用于计算和预测输入数据对应的输出；其中第2 到第4 层称为隐藏层,它们共同构建了隶属函数和模糊规则。

图1 ANFIS 网络的体系结构

2 ANFIS 系统模型

2.1 试验数据的生成和训练

预测模型需要输入数据完成学习过程,在负载预测问题中可使用安装在家庭中的数据记录设备来获取用电读数。每户家庭的智能电表会收集电力功耗信息,并将其发送到服务器,本文则将服务器上收集和累积的数据用于构建ANFIS 模型。

2.2 数据预处理

智能电表数据的语料库提供了该用电建筑中单个电路消耗的电力,其独立读数至少包含以下三个条目:

①测量读数的时间,采用Unix 时间戳

②电路消耗的功率,千瓦(kW)

③电路的标识

如果智能电表测量时电路的功耗为零(即电路不工作),则在该时刻没有功耗输入,此时如果将原始数据用于信息处理,将导致数据长度各不相同,因此习惯上通过如下公式推导具有固定时间长度的特征数据:

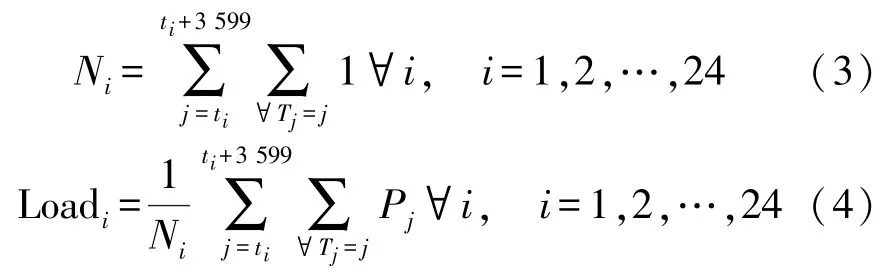
式中:Pj是电路在时间j消耗的功率；Ni是测量次数,是式(3)计算了所有用电设备在3 600 s 内的测量次数；式(4)则计算了设备在1 h 内的平均功耗。最后将导出数据的信息串联起来,形成数据长度固定的特征时间向量

2.3 数据归一化

将数字数据用于模式识别时,其动态范围会影响分类器的性能,其中动态范围是指功耗的最小值和最大值之间的差,如果动态范围太大,则在训练过程中较高的值会在数值上主导较低的值。因此为了利用所有特征值,通常将动态范围标准化为[0,1]之间的数字,归一化过程由式(5)实现:

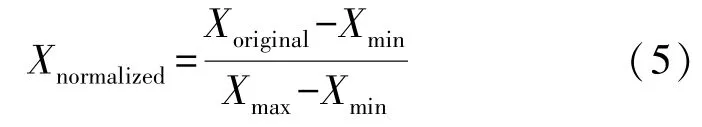
式中:Xoriginal是数据数值；Xmin是数据中的最小值；Xmax是数据中的最大值；Xnormalized是归一化数值。

2.4 ANFIS 系统的训练和测试

ANFIS 模型的训练和测试与数据同步完成,并建立模糊推理系统,其隶属函数参数则可通过反向传播算法,或结合最小二乘法进行调整。训练数据一般分为实验组和测试组,本文利用实验数据中的80%对系统进行训练,数据中剩余的20%作为未知的测试数据,来评估ANFIS 系统的性能。将归一化后的训练数据输入ANFIS 系统,调整隶属函数参数,生成ANFIS 模型的模糊if-then 规则,最后将测试集用于判断ANFIS 模型的性能。

3 实验结果和分析

本文从三栋房屋获得了耗电量测量值,分别为住宅A、B 和C[20]。测量值包括每秒钟测量的平均值和视在功耗、每个电路的功耗、每2.5 s 测量的所有插头负载的实际功耗等。同时在房屋内安装跟踪系统,跟踪设备灯光、运动感应、触发感应和恒温器传感器的开/关事件。除了能源消耗数据外,还提供发电数据,如太阳能电池板和微型风力涡轮机每5 s的平均发电量,以及通过室内外气象传感器每分钟测量的环境数据。本文主要分析家庭A 每秒测量的实际功率。原始数据集包含了从2020 年4 月1日到2020 年6 月31 日三个月的用电读数,其中用电读数不完整的天数不用于实验。

本文利用MATLAB 软件平台的模糊逻辑工具箱TM(MATLABR Fuzzy Logic Toolbox,TM)建立ANFIS 系统。由于MATLAB 将ANFIS 的输出数量限制为一个,因此本文开发了一种适用于24 h 数据输出的FIS 结构,其隶属函数的数目固定为2,隶属函数类型固定为高斯函数。在训练过程中,利用混合ANFIS 学习算法对FIS 参数进行调整,用以建立输入/输出关系。训练集则多次(迭代输入或周期输入)输入ANFIS 模型,直到达到期望的预测精度。最后将测试数据集用于模型验证,以查看ANFIS 模型预测相应数据集输出值的效果。

测试数据集可检查模糊推理系统的泛化能力,通过设置两个不同的公差间隔来反映预测结果,对于低值负载,例如低于1 kW 时公差设置为±100 W,设置允许的预测偏差为实际值的±10%,最后计算预测模型的正确预测数,就可以得到所提出的模型的总体性能。图2 所示是随机选择的天数的负荷预测值,表1所示是所有测试样本的平均预测精度。由表1 可见,总体预测精度达到了84.02%。从表1 中还可以明显看出,预测模型在一天中的某些小时内的预测性能相对较高,这是因为用电户在白天的用电行为模式具有较大随机性,导致了预测性能的变化。

表1 各个时间段的预测性能统计表

图2 负荷预测与实际值的对比示意图

表1 中的精度计算如式(6)所示:

式中:η是精度；XANFIS是模型计算值；Xreal是真实值。

4 结论

本文从模糊推理和人工神经网络理论出发,建立了针对智能电表大数据的分析方法和数学模型,基于智能电表实测数据进行了负荷预测研究。结果表明所构建的大数据预测模型能够有效针对用电户的负荷进行高时间分辨率的预测,其中夜晚时段预测精度均在90%以上,白天时段预测精度在70%左右,造成二者差异的来源是白天用户用电行为的随机性更强。