四顶点定理的物理意义

刘白羽

四顶点定理的物理意义

刘白羽

（北京科技大学 数理学院，北京 100083）

四顶点定理是平面闭曲线的一个重要性质．将平面卵形线的顶点与平面卵形薄板的平衡点联系起来，利用四顶点定理可得到均匀卵形薄板至少有４个平衡点，从而给出四顶点定理的物理意义．

微分几何；四顶点定理；顶点；平衡点

四顶点定理是微分几何平面曲线论中一个著名的经典结果，即平面上简单光滑闭曲线至少有４个顶点．这里，曲线的顶点是指曲率函数的局部极值点．1909年印度数学家Mukhopadhyaya[1]针对严格凸曲线证明了四顶点定理，1912年Kneser[2]证明了一般的简单闭曲线情形．此后，四顶点定理的逆定理也被证明[3]．在微分几何课程的教学中，为简单起见，只考虑卵形线，即简单的正规平面闭曲线且具有严格正的（相对）曲率．因此，四顶点定理叙述为：卵形线至少有４个顶点[4-5]．

1　平衡点及其数学描述

考虑一块只受重力和地面支撑力作用的平面均匀薄板，垂直放置于水平的地面上，当其处于静止时，薄板与地面接触的点，称为平衡点．考虑边界曲线为卵形线的均匀薄板（下称卵形薄板）的平衡点的个数问题．

图1 卵形薄板的平衡点

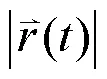
从力学角度可以证明平衡点的个数至少有４个[7]．文献[8]中也提出这一力学结论可作为微分几何中的四顶点定理的推论，但尚无文献给出由四顶点定理得到这一结论的详细证明．本文将给出这一详细证明．

2　平衡点与顶点的关系

利用平衡点的数学描述不难验证图2中椭圆形薄板的平衡点恰好有４个，且边界曲线的顶点就是薄板的平衡点．

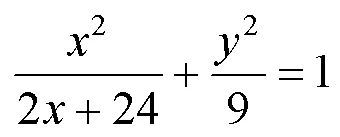
图2 椭圆形薄板及其平衡

图3　三次卵形线及其曲率函数

因此，卵形线的顶点不一定是卵形薄板的平衡点，卵形薄板的平衡点也不一定是边界卵形线的顶点．从直观上来看，曲率描述曲线在一点处的弯曲程度，是曲线的局部性质，而平衡点与整个薄板区域有关，是整体性质，两者显然是不同的．

3　卵形薄板至少有４个平衡点

[1] Mukhopadhyaya S．New methods in the geometry of a plane arc[J]．Bull Calcutta Math Soc，1909（1）：21-27．

[2] Kneser A．Bemerkungen uber die Anzahl der Extrema der Krummung auf geschlossenen Kurven und uber verwandte Fragen in einer nichteuklidischen Geometrie[J]．Festschrift Zum，1912，70：170-180．

[3] Dahlberg B E J．The converse of the four vertex theorem[J]．Proceedings of the American Mathematical Society，2005，133（7）： 2131-2135．

[4] 梅向明，黄敬之．微分几何[M]．5版．北京：高等教育出版社，2019．

[5] 蒋德瀚．整体微分几何中两定理的证明补阙[J]．甘肃高师学报，2002，7（5）：1-3．

[6] 周衍柏．理论力学教程[M]．北京：高等教育出版社，2009．

[7] Várkonyi P L，Domokos G．Static equilibria of rigid bodies：dice，pebbles，and the Poincaré-Hopf theorem[J]．Journal of Nonlinear Science，2006，16（3）：255-281．

[8] Domokos G，Papadopulos J，Ruina A．Static equilibria of planar，rigid bodies：is there anything new?[J]．Journal of elasticity，1994，36（1）：59-66．

[9] 李湘江．卵圆方程研究[J]．图学学报，2016，37（4）：467-470．

Physical meaning of the four vertex theorem

LIU Baiyu

（School of Mathematics and Physics，University of Science and Technology Beijing，Beijing 100083，China）

The four vertex theorem is an important globalof planar closed curve．the connection between the static balance points of an oval shape thin plate and the vertex of a planar oval is shown．By using the four vertex theorem， it was proved that there are at least four equilibrium points in a uniform ovoid thin plate，thus giving the physical meaning of the four vertex theorem．

differential geometry；four vertex theorem；vertex；static balance point

1007-9831（2022）09-0008-04

O186.1

A

10.3969/j.issn.1007-9831.2022.09.002

2022-01-17

北京科技大学青年教学骨干人才培养计划项目（2302020JXGGRC-001）；北京科技大学本科教育教学改革重大项目（JG2019ZD05）

刘白羽（1982-），女，上海人，教授，博士，从事偏微分方程与几何分析研究．E-mail：liuby@ustb.edu.cn