电力电子模块封装硅胶电荷输运与陷阱特性研究

赵 军，何瑞东，高树国，相晨萌，王亚林，尹 毅

（1.国网河北省电力有限公司电力科学研究院，河北 石家庄 050021；2.国网河北省电力有限公司，河北 石家庄 050022；3.上海交通大学 电气工程系，上海 200240）

0 引言

随着市场对高功率密度集成功率模块的强劲需求，高压功率模块的封装绝缘受到越来越大的电应力和热应力，其可靠性面临严峻挑战。由于存在金属-氧化物半导体场效应晶体管（MOSFET）的体二极管或绝缘栅双极型晶体管（IGBT）并联二极管，高压功率模块封装绝缘材料通常会承受单极性电应力，即直流情况。功率模块封装绝缘通常使用聚合物材料，然而，聚合物绝缘在直流情况下容易积累空间电荷，导致电场畸变加速绝缘老化，并最终大幅缩短其寿命[1-3]。因此，聚合物中的空间电荷对其绝缘性能起着至关重要的作用。由于目前宽禁带功率模块商用化产品的额定电压大多为1 200 V或1 700 V，空间电荷的问题并没有引起功率模块封装绝缘研究的太多关注。然而随着高压宽禁带功率模块的研发和应用，封装绝缘要求耐受10 kV及以上电压等级，功率模块的功率密度要求也随之提高，解决封装绝缘面临的空间电荷、电场畸变、温度集中和机械应力集中等问题，对于提升封装绝缘的可靠性很有必要。

随着空间电荷检测技术的发展，电声脉冲（pulsed electro-accoustic，PEA）法已经在世界范围内成熟发展并得到广泛应用，可以通过测试直接获得电介质中的空间电荷分布[4]。近几十年来，等温松弛电流（isothermal relaxation current，IRC）理论在各种电介质和半导体的微观结构和载流子传输动力学方面得到了相当多的关注[5]，通过IRC分析方法可以获得电介质中的陷阱能量密度分布。空间电荷积累与聚合物中的浅陷阱和深陷阱密切相关，因此同时测量空间电荷和陷阱能量密度将有助于全面详细地了解载流子传输的机理。然而，目前对同一试样进行空间电荷和陷阱能量密度联合测试的研究较少，缺乏成熟的联合测试设备，使得该项研究进展缓慢[6-7]。Y TANAKA等[6]最早提出空间电荷与热刺激电流联合测量的概念，并以此研究有机玻璃经γ射线辐照后的电导行为，然而研究装置无法研究样品在极化过程中的空间电荷与电流特性。J M ALISON[8]研发了空间电荷与电导电流联合测量的实验装置，然而整个测试装置是安装于烘箱门的内侧，因此温度的控制不精确。目前尚没有针对封装硅胶进行空间电荷测试的研究报道，也没有对封装硅胶的空间电荷特性与陷阱特性进行联合分析的研究。

本文对功率模块封装绝缘硅胶进行空间电荷和IRC联合测量，研究不同温度和外施电压下封装硅胶的空间电荷特性。此外，提出一种基于非负最小二乘迭代的IRC新分析方法，基于该方法计算封装硅胶的陷阱能态分布，分析温度对封装硅胶空间电荷特性和陷阱电荷分布的影响，为高压功率模块封装绝缘的可靠性研究提供参考。

1 实验

1.1 试样制备

测试试样由密度为0.90 g/cm3的双组分硅胶（基料和固化剂）制成。首先，将基料放入凹槽形状的聚四氟乙烯夹具中以固定和控制厚度。然后，将固化剂（占基料质量的10%）加入基料中，混合物在室温下固化24 h。最后，将混合物放入真空烘箱中，在60℃下脱气除去残留杂质。试样的厚度约为300μm，制成的试样如图1所示。

图1 硅胶试样Fig.1 The silicone sample

1.2 空间电荷与电流联合测试系统

空间电荷和电流的同时测量可以避免由于试样本身特性和制样过程的分散性所造成的测试结果差异。本文开发了一种基于PEA空间电荷测量方法和“四电极”设置的同步测量系统[9]。测试系统中有4个电极与试样接触，分别是上电极、保护电极、下电极和电流测量电极，如图2所示。上电极连接直流高压和纳秒脉冲电压，保护电极接地，下电极与压电传感器的一面接触并接地，电流测量电极连接电流测量设备的输入端。这种电极布置方式可以看作是PEA法的改进版（在正常的下电极之外添加两个圆环电极）。除了电极设置问题之外，纳秒脉冲电压（脉冲宽度为几纳秒量级的空间电荷激励源）施加在试样上时会产生脉冲电流。根据之前的研究[9]，具有快速上升和下降沿的脉冲电压施加在试样上时不可避免地会导致较大的脉冲电流流过电容试样和电流测量设备。由于纳秒脉冲电压在空间电荷测量中是必不可少的，应采取措施避免该脉冲电流，否则会损坏电流测量设备。纳秒脉冲电压对电流测量的影响在相关文献中有详尽的描述[9]，本文采用单刀双掷开关协调两种测量方式的矛盾来解决上述问题，如图2所示。测量采用“分时”的策略[10]：测量空间电荷时，对试样施加纳秒脉冲电压，电流测量电极接地；测量电流时，将电流测量电极连接到电流测量设备，同时将输出的纳秒脉冲电压设置为0，空间电荷测量和电流测量交替进行。设置电加热圈作为热源，测温热电偶埋入下电极靠近试样的位置，对试样温度进行检测，并与温度控制器相连接，控制试样的温度。

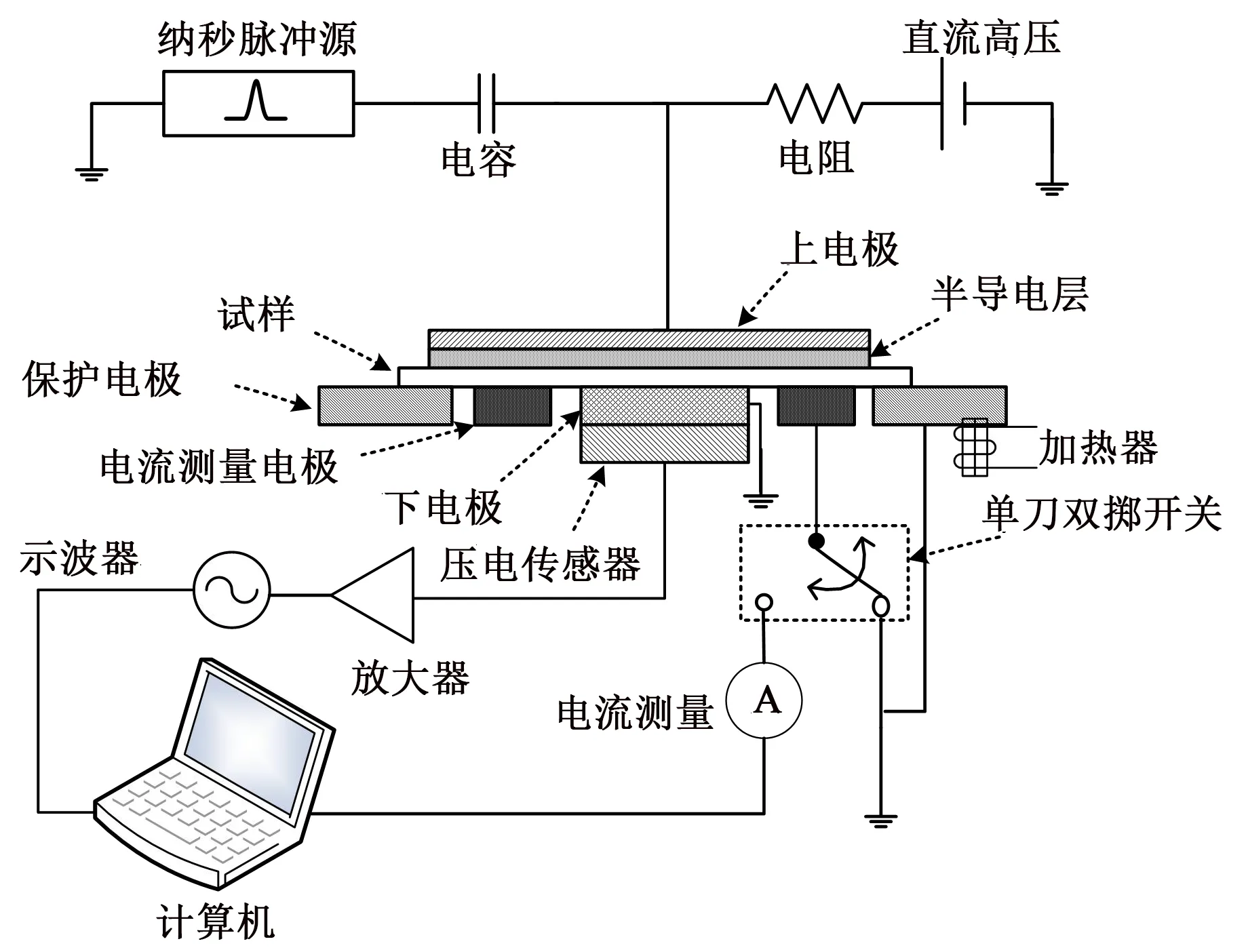
图2 联合测试系统结构示意Fig.2 Simultaneous measurement system

测量程序如图3所示。每1 800 s对试样施加3～15 kV/mm的阶梯上升电压，最后将试样短路3 600 s。测量分别在40、60、80℃温度下进行，在整个实验过程中测量空间电荷和电流。

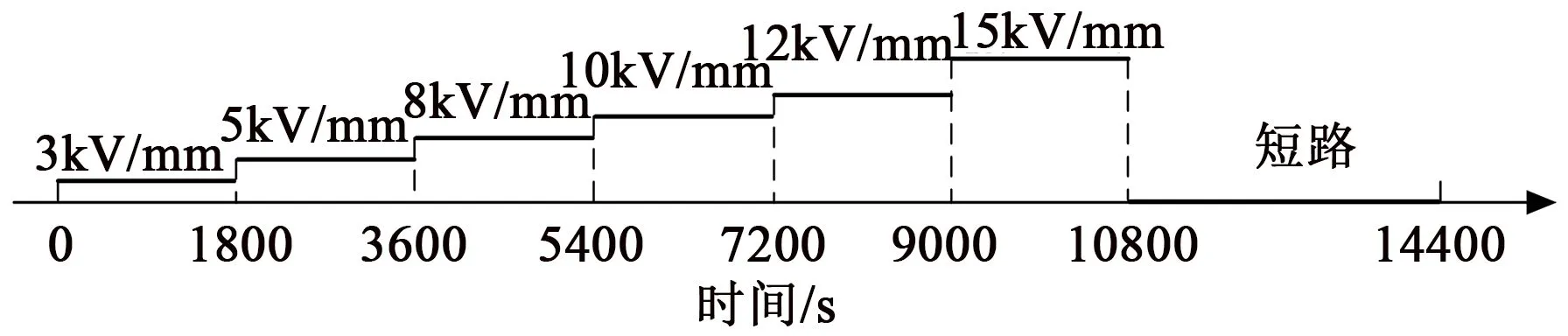
图3 测试施加电压流程Fig.3 Experiment procedure of voltage application

2 结果与分析

2.1 不同温度下空间电荷分布

图4为不同温度下封装硅胶试样中以颜色编码形式显示的空间电荷时空分布。图4中，横轴表示测量时间，从0 s到14 400 s；纵轴表示位置，阳极和阴极的位置用平行的白色虚线表示，垂直的黑色虚线表示测量不同的极化阶段和短路阶段；平行虚线上的空间电荷是在电极和试样之间界面上感应的容性电荷。从图4可以看出，在阴极和阳极附近出现了同极性的电荷积累，随着外加电场的增大，电荷积累量逐步增加。一般认为电极附近积累的同极性电荷是由注入的电子或者空穴形成的。随着温度的升高，正电荷逐渐占据主导，即试样中正极性空间电荷积累数量大于负极性电荷。

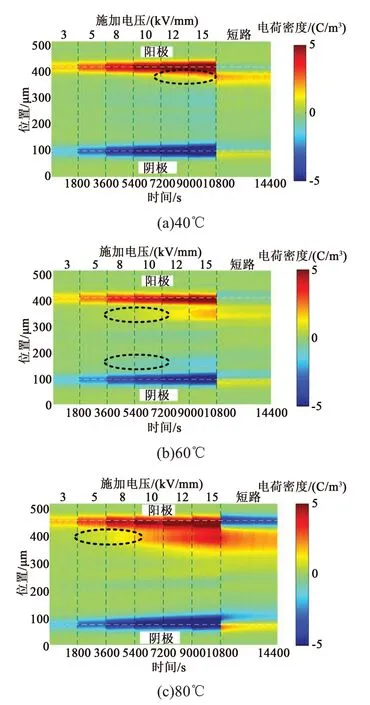
图4 不同温度下的空间电荷时空分布Fig.4 Spatial and temporal distribution of space charge at various temperatures

对实验结果分析还发现，空间电荷积累阈值电场随着温度的升高逐渐减小：40℃时施加电场强度在10 kV/mm以上后出现明显的电荷积累；60℃时积累阈值电场强度位于8～10 kV/mm；80℃时阈值电场强度位于5～8 kV/mm。此外，空间电荷的注入深度也随着电场强度的增大和温度的升高而增加，随着温度的升高，在更深处积累了较多的电荷。值得注意的是，即使在80℃短路3 600 s后，仍有相当数量的电荷没有完全消散。

2.2 不同温度下试样内部电场分布

根据泊松方程，可以从试样内部测得的空间电荷信息中计算出试样内部的电场分布，如式（1）所示。

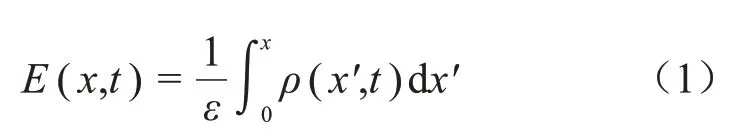
式（1）中：E是电场强度；ε是材料的介电常数；x是到电极（阴极）的距离；ρ是试样中测得的电荷密度。

为了定量分析试样在不同温度和不同外加电场下的电场畸变程度，将电场畸变程度定义为式（2）[11]。

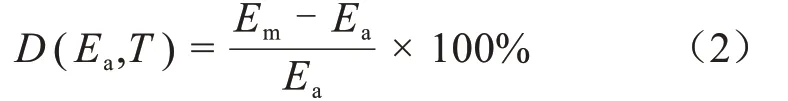
式（2）中：D是电场畸变系数；Em是由泊松方程导出的试样内部电场的最大值，Ea是外加电场强度。

计算不同温度下试样中的电场分布如图5所示，不同外加电场和不同温度下的电场畸变系数如图6所示。从图5可以看出，随着同极性电荷的注入，电荷与电极之间的电场被削弱，而正、负电荷之间的电场增大。从图6可以看出，随着温度升高和电荷注入加剧，电场畸变系数整体呈现增大的趋势，最大的电场畸变系数对应于最高的实测温度和最大的外加电场。温度为80℃时，电荷积累量和深度比40℃和60℃时更多，电场畸变程度更严重。空间电荷积累对试样内部的电场分布有重要影响，空间电荷是材料在直流高压下内电场发生畸变的主要原因，畸变的电场对功率模块封装绝缘的局部放电和老化有显著影响，并影响高电压下功率模块封装的可靠性。

在实训教学中，教师设计出的任务要具有一定的灵活性，任务的完成情况没有一个具体的参考标准，教师要引导学生进行客观的自我评价和反思。最后，将学生的自我评价、同学评价和教师评价三者有机整合，在学习过程中，学生的创新能力、知识迁移能力会得到不同程度的体现，这是自主学习能力最重要的一部分。

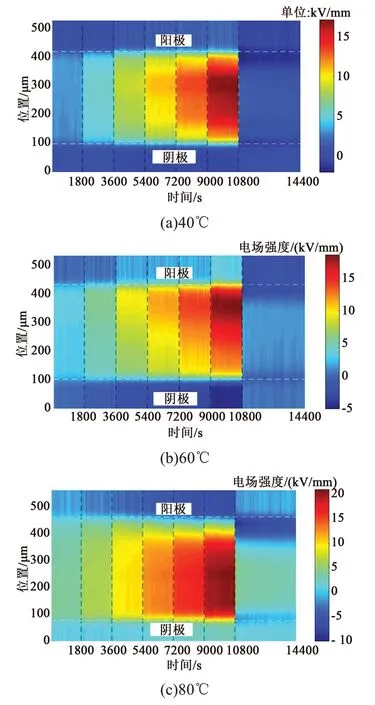
图5 不同温度下的试样电场时空分布Fig.5 Spatial and temporal distribution of electric field at various temperatures

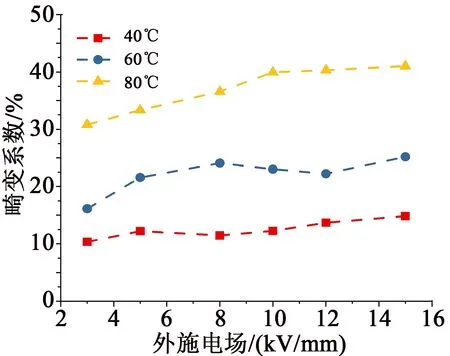
图6 不同温度和外施电场下的电场畸变程度Fig.6 The electric field distortion degree under different temperatures and applied electric fields

2.3 基于非负最小二乘迭代方法的IRC分析

在不同温度下短路阶段测得的等温松弛电流如图7所示。从图7可以看出，不同温度下IRC曲线的值均为pA级，并且脱陷电荷引起的IRC不呈现随温度变化而单调增减的特性。IRC曲线包含了空间电荷的脱陷信息，而这些电荷是在加压阶段注入并被困在不同深度（或能级）的陷阱中。入陷在不同深度陷阱的电荷具有不同的松弛时间，每一时刻的松弛电流由不同深度陷阱中的电荷脱陷共同构成。陷阱深度为Et的入陷电荷松弛衰减可表示为式（3）[12]。

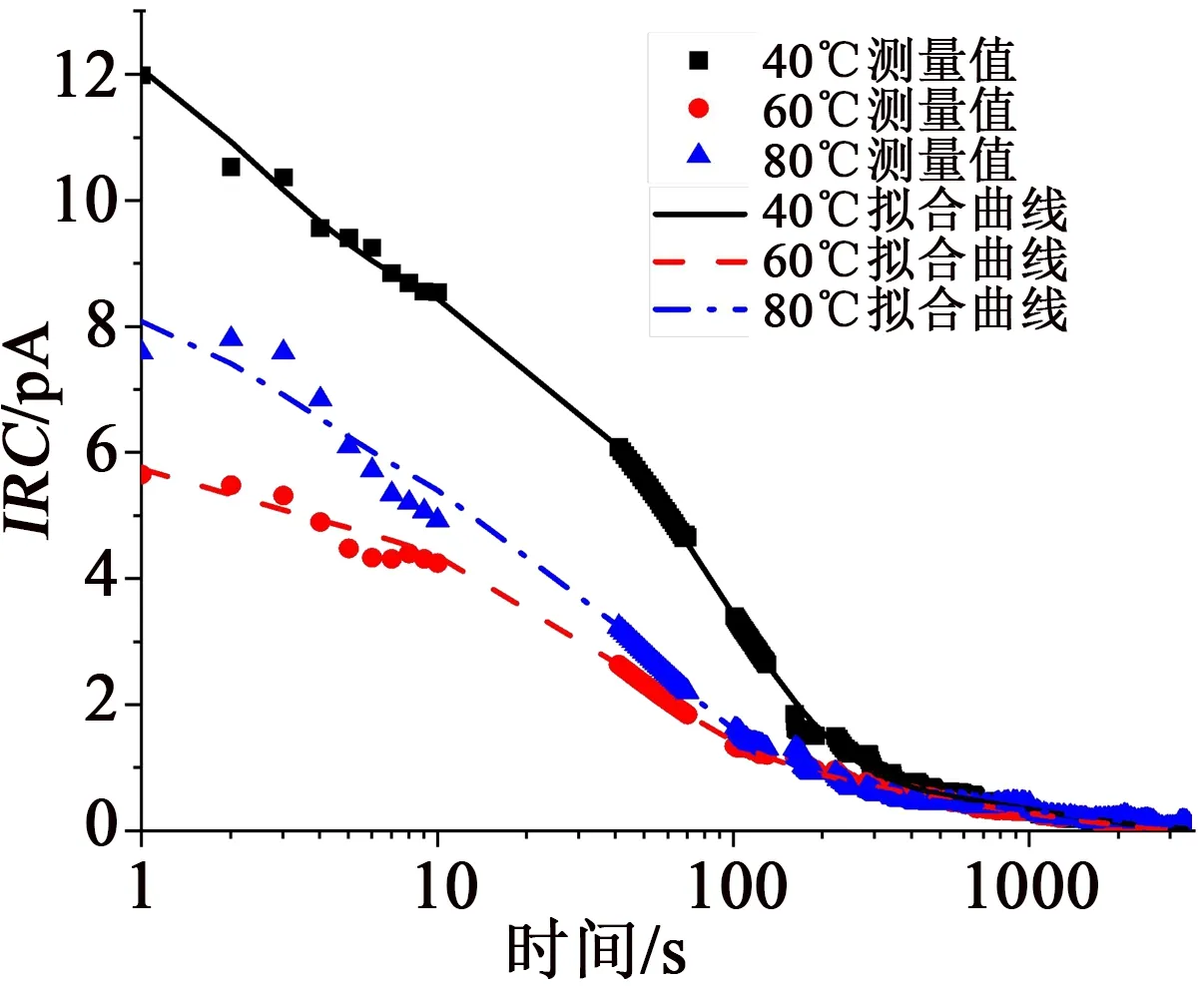
图7 不同温度下的IRC测量曲线和拟合曲线Fig.7 IRC measured curves and fitting curves under various temperatures

式（3）中：nt是入陷电荷的密度；v是热运动的速度；Nc是导带能态密度；St是陷阱的俘获截面；Et是陷阱深度；k是玻尔兹曼常数；T是温度；将上述各参量整合成D表示入陷电荷变化率。

在恒温情况下，nt可表示为式（4）。

式（4）中，nt0是初始入陷电荷密度。

厚度为dx的位于x位置的电荷脱陷引起的电流如式（5）所示[11]。式（5）中：J是IRC密度；q是基本电荷，为1.6×10-19C；L是试样的厚度。

将式（5）进行积分，并将nt替换为式（4），得到式（6）。

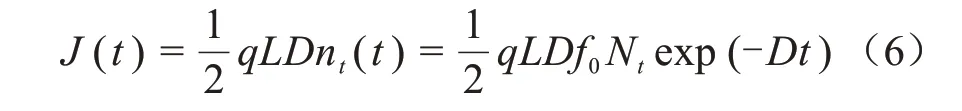
式（6）中：Nt是陷阱的密度；f0是具有相同深度的陷阱的初始占有率。

需要注意的是，式（6）中的D包含陷阱深度Et，说明式（6）适用于单个陷阱深度。如果想要将方程推广到整个能级，可以通过对价带顶部到导带底部的能级进行积分来推导出修正表达式，如式（7）所示。

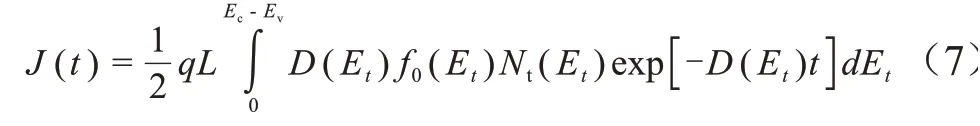
式（7）中，Ec和Ev是禁带的最高和最低能级。

式（7）可以进一步简化，q、L为常数，如果电荷注入过程足够长，f0可以设置为1。若使用矩形积分简化，式（7）可简化为式（8）。

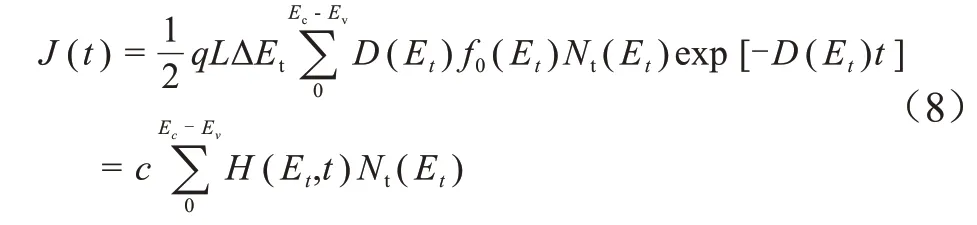
式（8）中：c是简并后的常数；ΔEt是两个连续陷阱深度之间的间隔；H是Et和t的二元函数。

式（8）可以写成矩阵形式，如式（9）所示。

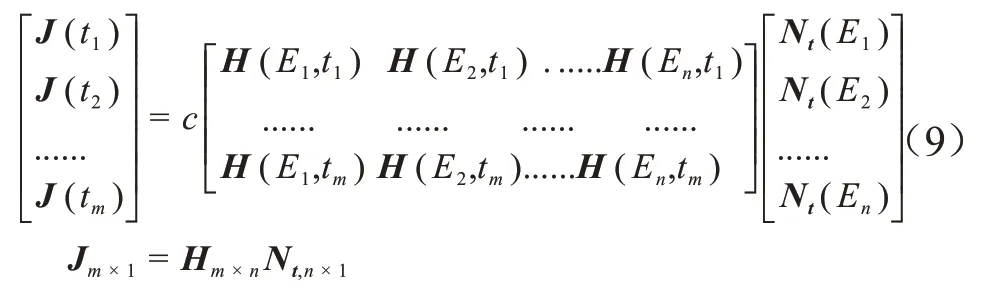
其中可以假设IRC数据J是一个长度为m的向量，表示m个时间尺度上对电流的采样，变量Nt是一个长度为n的向量，表示将禁带划分为n个能级。通常m不等于n，H的秩一般小于m或n，是秩亏矩阵。求解式（8）可以使用最小二乘算法，由于陷阱密度非负，解具有非负的限制，求解式（8）变成了求解非负最小二乘问题。文献[13]提出了一种解决非负最小二乘问题的有效迭代算法，可以在本文中应用。

该算法从一组备选的基向量开始，并计算相关联的对偶向量w。然后选择与w中最大值对应的基向量以换取另一个候选向量，一直持续到w≤0。算法输入为m×n矩阵H和m维向量J、n维向量w和z提供工作空间，索引集P和Z将在算法执行过程中被定义和修改。解Nt满足式（10）。

Nt是最小二乘问题的解向量，其满足式（11）。

对偶向量w满足式（12）。

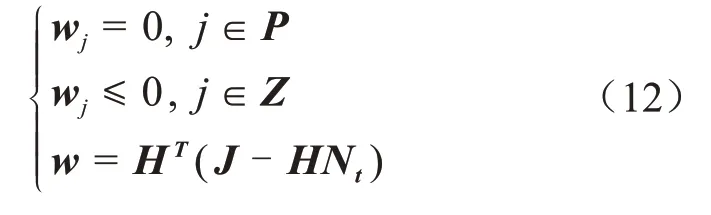
式（10）～（12）构成了描述非负最小二乘问题解向量Nt的Kuhn-Tucker条件。该算法的详细收敛证明参见文献[14]，详细循环迭代过程如图8所示。

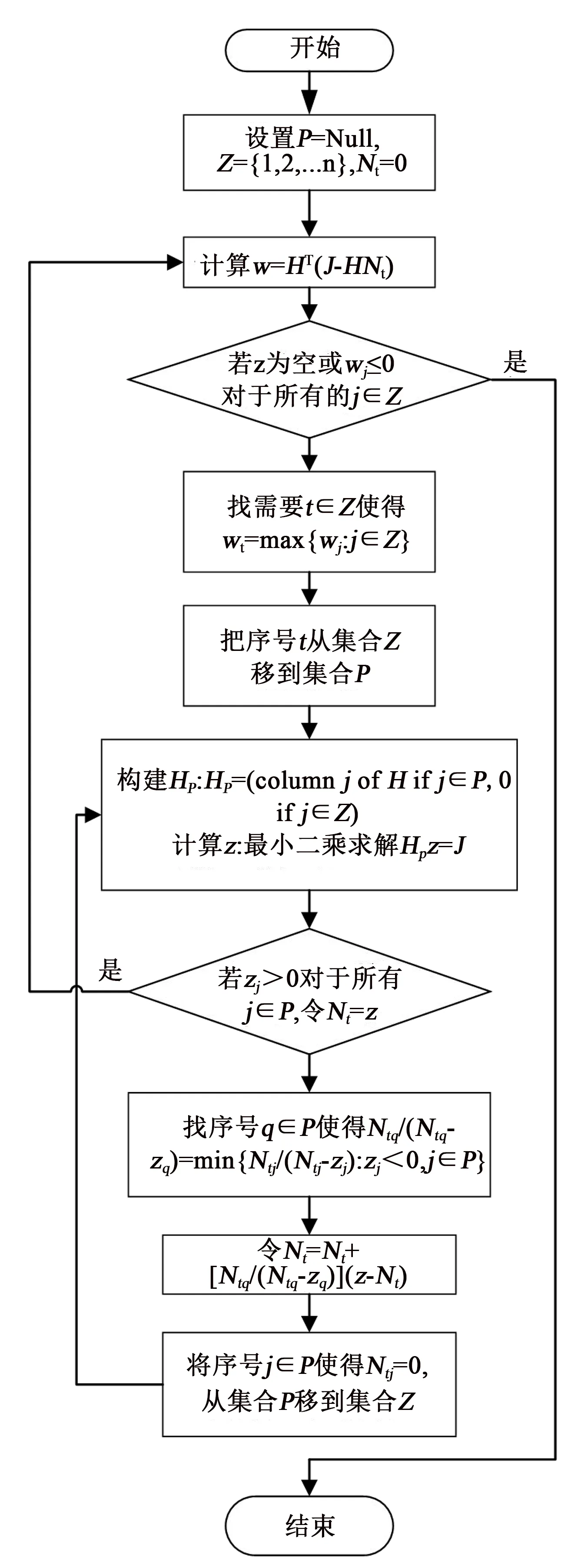
图8 非负线性最小二乘迭代算法求解流程Fig.8 Procedure of solving non-negative linear least square problem by iteration method

对不同温度测量获得的IRC曲线用式（8）进行分析，计算出的陷阱深度和陷阱密度如图9所示。为了验证分析结果，将计算出的陷阱深度和密度反向验算，计算得到IRC的拟合曲线，将其与IRC的测量值进行比较并显示在图7中。通过计算R2值来评估实验数据和拟合曲线之间的重合程度（R2值是响应值与预测响应值之间相关性的平方）。图7中曲线计算的R2值分别为0.990 6、0.987 9、0.986 9，都非常接近1，表明实验数据和拟合曲线十分相似。

计算出的封装硅胶的陷阱能谱可以分为4个区域，如图9所示。区域A中陷阱的深度为0.8～0.9 eV，入陷的电荷较少，电荷相对容易从这些深度较浅的陷阱中脱陷；区域B中的陷阱深度为0.9～1.0 eV，不同温度下测量的IRC电流在此区域内均有较多的分量，陷阱分布也比较密集。从图4(a)中可以看出，在短路3 600 s后仍有电荷剩余。这是因为40℃的热刺激不足以让相对较深的陷阱中的所有电荷脱离陷阱。60℃时的空间电荷和IRC结果表明，大部分入陷电荷被困在区域B和区域C。随着温度的升高，较浅陷阱中的电荷更容易在电场和温度的作用下脱陷，因此表现为在更高温度下深陷阱中的电荷更多。对于在80℃下测量的IRC，有部分分量对应在区域D中的陷阱电荷脱陷，其陷阱深度超过1.15 eV，可以认为是很深的陷阱，并且在短路3 600 s后，仍然有相当量的空间电荷在试样中。

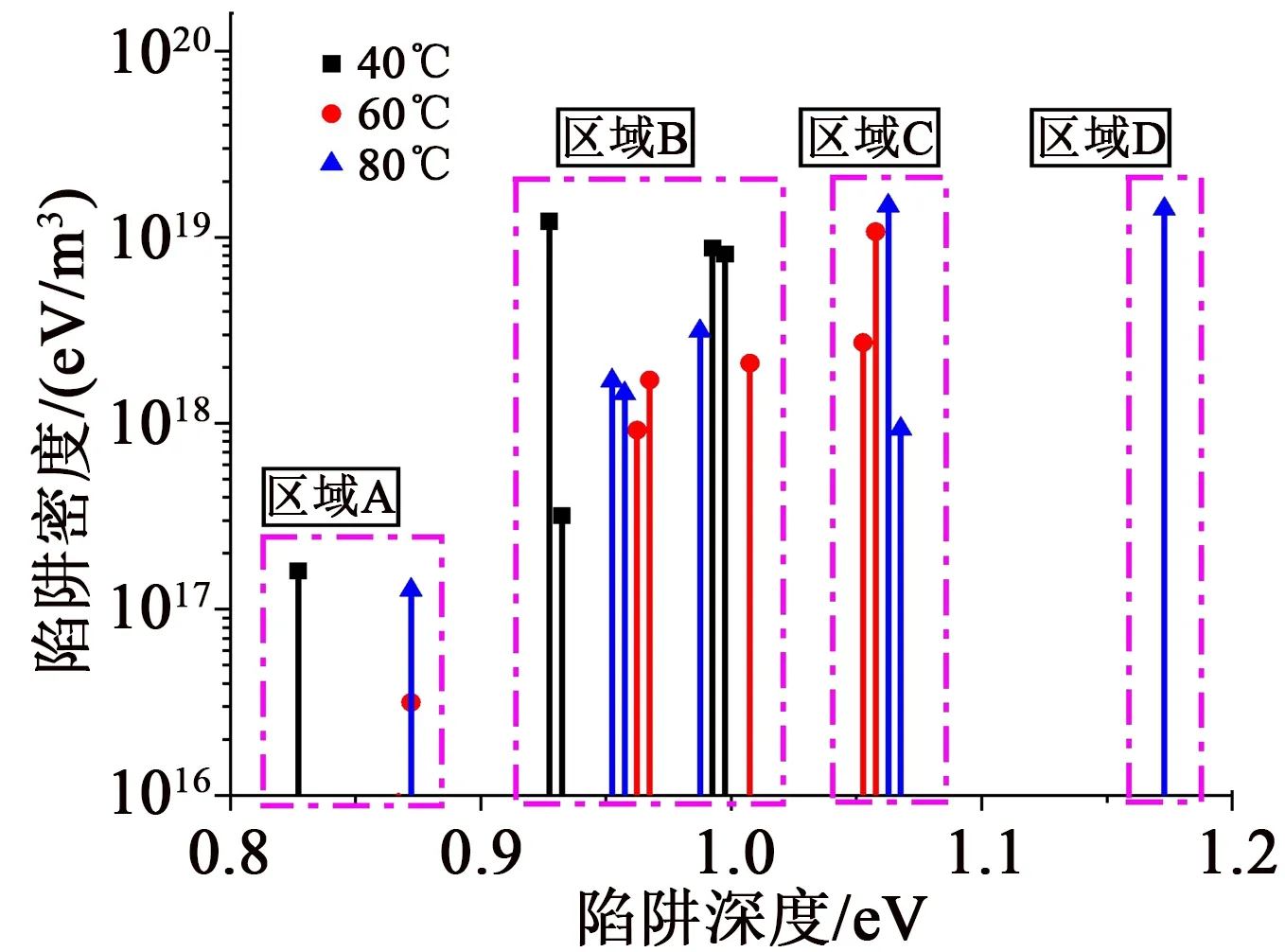
图9 封装硅胶陷阱能态密度分布Fig.9 Trap energy density distribution ofsilicone for encapsulation

3 讨论

3.1 温度对封装硅胶中空间电荷特性的影响

封装硅胶属于硅聚合物的一种，电力电子模块中使用的封装硅胶大致分为硅凝胶材料和硅弹性体材料（或通俗称为橡胶）。硅凝胶是一种介于固体和液体之间具有很低硬度的封装材料。硅弹性体是以分子量较小的聚硅氧烷为基础胶，在交联剂和催化剂的作用下，在室温或稍许加热条件下采用有机过氧化物硫化成形，如图10所示。由于硅胶以无机硅氧烷链（Si-O-Si）为主链，Si-O键的键能大于C-C键的键能，因此相较于常见的有机聚合物，封装硅胶具有更好的耐热性和耐候性。本文研究的封装硅胶属于硅弹性体，具有一定的弹性并且具有相对硅凝胶更高的击穿电压，被应用于高压功率模块的封装绝缘。相对于半结晶半无定型的部分有机聚合物如交联聚乙烯，封装硅胶是无定型聚合物，内部构型不是十分规则，由高分子长链和部分侧链相互交联构成，内部陷阱能级分布较为广泛。

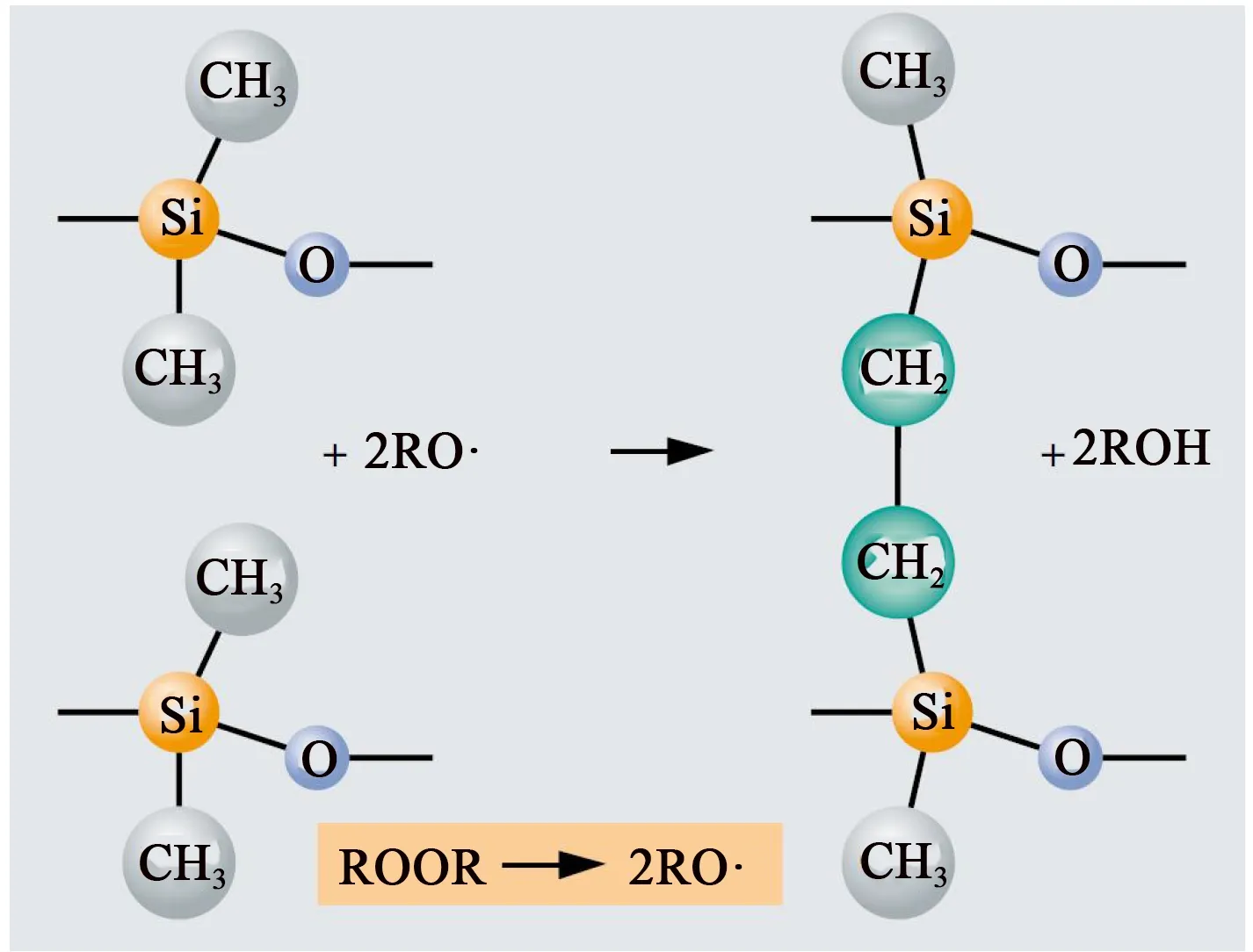
图10 封装硅弹性体硫化过程Fig.10 Vulcanizing process of silicone elastomer for encapsulation

由图4和图5的测量结果可以看出，温度对直流电压下封装硅胶中的空间电荷分布和电场分布具有较大影响。值得注意的是，虽然封装硅胶能够在非常高的温度下保持绝缘不被击穿，但是温度对电荷的注入和迁移的影响仍然不能忽视。随着温度的升高，电荷更容易注入封装硅胶，并被陷阱捕获而积累。温度的升高也促进了电荷的迁移，导致电荷积累的位置越来越深。虽然温度对正电荷和负电荷的输运均具有促进作用，但图4表明正电荷积累的量大于负电荷，这是由于陷阱对正、负电荷的捕获能力不同或温度对界面处电荷注入、迁移和热促脱陷的综合影响导致的。但是不是温度越高，短路最后阶段剩余的电荷越少，反而是60℃时短路后积累电荷的剩余量最少。

3.2 温度对封装硅胶中陷阱特性的影响

陷阱的分布是对陷阱电荷释放而引起的IRC分析获得的，因此无法脱离电荷行为而只对陷阱本身进行讨论。由图9可以看出，40℃时积累的空间电荷分布在1.0 eV以下（条件是短路3 600 s），并且区域B是主要的电荷积累陷阱能级区域。由图4的空间电荷分布可以看出，短路3 600 s后仍然有空间电荷剩余，表明40℃的热刺激能量不足以使得较深陷阱中的电荷脱陷。由图9可以看出，60℃时积累的空间电荷主要分布在0.9～1.1 eV（在3 600 s短路时间内计算得出），区域B和C是主要的电荷积累陷阱能级区域。80℃时积累的陷阱电荷有部分位于区域D中，陷阱深度超过1.15 eV，在短路3 600 s后仍然有电荷剩余，表明80℃的热刺激能量不足以使得在区域D深陷阱中的电荷脱陷。60℃时积累的电荷在短路3 600 s后几乎全部消散，这是因为60℃时入陷电荷的能级和热刺激能量几乎匹配，即60℃提供的热运动能量能够使得电荷脱陷。而40℃和80℃时，由于有部分电荷位于与热刺激能量不匹配的陷阱中，即深陷阱中的电荷不足以依靠热运动能量脱离陷阱。

值得注意的是，在每个区域中不同温度下计算得出的陷阱分布相互靠得很近，并且位置较为固定，表明这些陷阱能级是封装硅胶的特征能级，与其微观结构有关。虽然陷阱在整个能带结构内广泛分布，但是以离散能级的形式存在。

3.3 封装绝缘中空间电荷与陷阱的关联

针对封装绝缘IRC的分析可以获得陷阱能级分布而不能够获得陷阱的空间分布情况，空间电荷测量能够获得空间分布信息，将两者结合能够更全面的反映电荷与陷阱的关系。由于表面态的存在，能带周期在聚合物绝缘表面被打断，表面存在较多的陷阱能级，由空间电荷测量结果可以看出，靠近电极表面的电荷积累较多，随着温度的升高，电荷分布也向内部扩展，总体而言，电极附近的电荷量多于试样内部的电荷量。封装硅胶绝缘内部的陷阱分布在较宽的能级范围内，从浅陷阱到深陷阱均有分布，总体而言，深陷阱的电荷量大于浅陷阱的电荷量。随着温度的升高，较浅陷阱中的电荷更容易在电场和温度的作用下脱陷，因此表现为在更高温度下，深陷阱中的电荷更多。

4 结论

（1）随着外施电场的增加，同极性电荷在电极附近积累。电荷注入的阈值电场随着温度的升高而逐渐降低。此外，随着温度的升高，更多的电荷会积聚在材料内部更深的位置。

（2）封装硅胶中广泛分布从0.8～1.2 eV不同深度的陷阱，提出的基于非负线性最小二乘迭代算法的等温松弛电流分析方法能够对整个能带内的陷阱进行分析。随着温度的升高，入陷电荷位于的陷阱能级整体呈现变深的趋势。

（3）随着温度的升高，试样内部的电场增大，累积的空间电荷畸变了局部电场，并对高压功率模块封装绝缘的可靠性产生影响。由于温度在空间电荷输运行为中起着重要作用，空间电荷积累在很大程度上影响局部电场畸变，因此在开发高压、高温功率模块时，应充分关注空间电荷行为。