永磁同步电动机数学模型及其控制策略
谢金涛
(天津工业职业学院,天津 300400)
0 引言
在电动机及其控制技术的发展过程中,高速控制器技术日渐成熟,其计算速度和计算能力大大提高,使得曾经非常复杂的控制算法得以运行,推动了先进的电机控制技术的丰富与发展,促进了永磁同步电动机性能的不断提高。
永磁同步电动机控制系统主要有三类主流的控制技术。一是变压变频控制,英文译作Variable Voltage Variable Frequency,简称VVVF,主要是通过同时调整电源电压及其工作频率来改变电机转速,VVVF控制策略在本质上属于开环控制。二是矢量控制技术,德国达姆施塔特工业大学的K.Hasse博士于二十世纪六十年代末最早提出矢量控制技术,并在交流异步电机调速系统中获得成功应用。矢量控制技术对于微处理器的计算和处理能力要求非常高,因此前期没有普及使用,而后期随着信息计算技术的快速发展,才被逐渐投入永磁同步电动机的使用过程中。三是直接转矩控制,直接转矩控制算法具有结构简单且计算量相对较小的优点,对转子位置的计算要求不高,这就使得转速测量装置可以被省略,大大地节约了系统的硬件成本。此外,因动态响应较快,永磁同步电机系统的直接转矩控制策略应用也比较广泛。下面笔者将从电动机的结构形式出发进行数学模型、建模方法及控制策略分析。
1 永磁同步电机的结构形式
永磁同步电机转子的旋转速度是同步转速,其磁链会在定子绕组中产生反电动势,不同类型的永磁同步电机产生的反电动势是不同的,根据反电动势的形式可以将永磁同步电机划分为正弦波永磁同步电机与方波永磁同步电机两种类型[1-2]。本文主要以正弦波反电动势的永磁同步电机作为系统的研究对象开展研究工作。
永磁同步电机在工业应用中的需求是不一样的,根据不同的需求,制作永磁同步电机转子的步骤以及转子结构形式都是不相同的。通常情况下,根据永磁同步电机转子中永磁体的安装位置,将永磁同步电机的转子结构划分为面装式、嵌入式与内置式三种。
将永磁体安装在永磁同步电机转子的表面位置的同步电机转子称为面装式转子。与面装式转子结构不同,将永磁体安装在转子铁芯内部的永磁同步电机转子结构在直轴与交轴上具有不相同的电感值。因为面装式永磁同步电机的特点,可以将面装式转子的永磁同步电机归属于一种隐极式永磁同步电机。相对应的,因为嵌入式和内置式转子的电感不同的特点,可以认为嵌入式和内置式转子的永磁同步电机属于一种凸极式永磁同步电机[3]。
2 永磁同步电机的数学模型
坐标变换理论是交流电机调速领域所应用的尤为重要的基础理论,在永磁同步电机的矢量控制算法与直接转矩控制算法使用过程中,该变换理论发挥了非常关键的作用。
坐标变换理论是典型的线性变换理论,但是为了使坐标变换前后的值线性对应且具有唯一性,就必须给坐标变换附加约束条件,这个约束条件就是磁动势等效。保证坐标变换的磁动势相同的目的是保证电机的磁场不发生变化,只有这样才能确保电磁转矩在变换前后计算的正确性。在永磁同步电机控制系统应用的控制理论中,需要定义三种类型的坐标系,它们分别为三相静止的坐标系,用A-B-C表示;两相静止的坐标系,用α-β来表示;两相旋转的坐标系,用d-q来表示,d和q也就是直轴和交轴的字母表示形式,这三个类型的坐标系的空间对应关系,如图1所示。

图1 空间中三种类型坐标系的矢量关系
三相静止的坐标系的三个坐标轴A、B、C按照逆时针的方向旋转,并且相差120°的电角度,可以代表三相的电压、电流和磁链。为了便于图形化地表示和理论计算,将两相静止坐标系的α轴的位置角度与三相静止坐标系的A轴位置角度定为相同,然后将β轴按照逆时针的方向旋转90°电角度,这就构成了两相静止的α-β坐标系。两相旋转的d-q坐标系是同步旋转的坐标系,之所以叫同步旋转的坐标系是因为坐标系与转子磁链的旋转速度是相同的。
如前文所述,上述三种类型的坐标系进行变换的依据是磁动势守恒的基本原则,通常情况下,变换的类型有以下几种:
1)Clark变换及其逆变换。Clark变换表示将三相静止坐标系A-B-C经过投影变换为两相静止坐标系α-β的变换理论,通常也称作3s/2s变换。假设三相绕组的缠绕匝数为N3,两相绕组的缠绕匝数为N2,在确保Clark变换前后的磁动势相同的基本原则下,三相绕组和两相绕组在α和β轴上的投影长短是相同的,因此有式(1)成立:
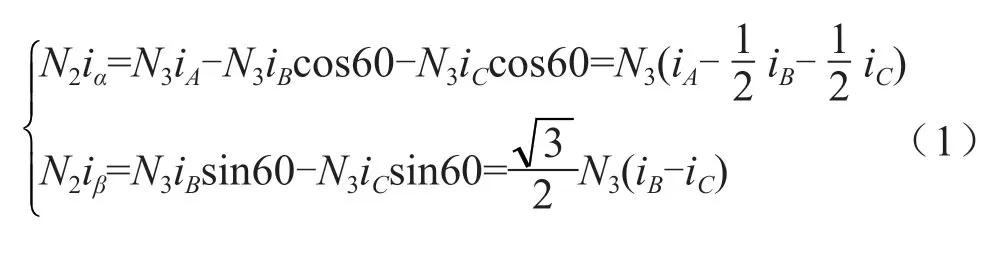
式(1)中矩阵前系数为绕组缠绕的匝数之比。该系数有两种不同的计算情况,第一种情况是进行坐标变换的前后需要保证总功率不变,第二种情况是坐标变换的前后需要保证幅值不变。本文所涉及的计算过程都用等幅值变换的方法,因此此时的Clark变换公式可以变形为式(2)的形式:
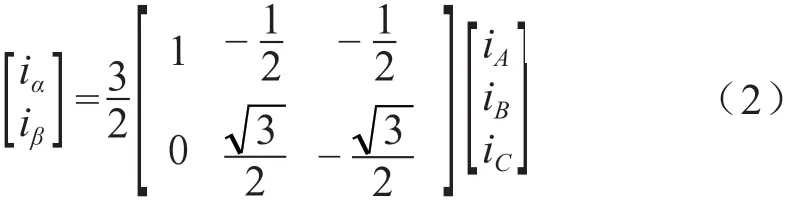
相关文献的理论证明显示式(2)的关系适用于电流、电压和磁链的坐标变换。
与Clark变换相对应的逆变换称为Clark逆变换,变换的过程是将两相静止的坐标系α-β向三相静止的坐标系ABC进行线性变换,一般情况下称该变换为2s/3s变换,正好与Clark变换的运算过程相反。
2)Park变换及其逆变换。Park变换也是一种线性变换,它将两相静止的坐标系α-β向两相旋转坐标系(也可以称为同步旋转坐标系)d-q进行线性变换,该变换过程也称为2s/2r变换[4-5]。不失一般性地假设两相旋转的坐标系的直轴(也称为d轴)和两相静止的坐标系的α轴之间的变化夹角为θ,则将两相旋转的坐标系的矢量分别向两相静止的坐标系的α和β轴方向进行投影,经过投影计算后,可以得到式(3):
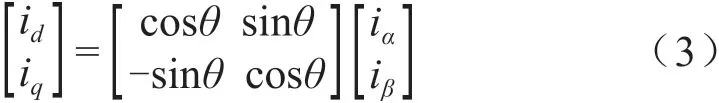
与Clark逆变换的道理相同,Park逆变换也称作2r/2s变换[3,5]。
综上所述,可以将两种变换的形式综合计算,得到三相静止坐标系向两相旋转坐标系变换的全部过程,至此,得到了永磁同步电动机控制策略所应用的坐标变换的基础理论。
3 PMSM建模方法
永磁同步电机的结构并不是十分复杂,但是其定转子之间的电磁关系却比较复杂,复杂性主要体现在系统参量关系之间的非线性和强耦合的特点,因此,为了得到比较好的分析效果,需要将永磁同步电机的复杂物理关系进行简化,去除次要矛盾,保留主要矛盾,构建比较理想化的电机模型。因此,为了便于分析又不失一般性,本文在进行电机建模之前,假设下列条件成立[6-7]:
1)定子上的三相绕组严格对称,并且连接形式为星形,在定子绕组中感应出来的电动势必须按照正弦分布。
2)不考虑铁芯的磁饱和性,不考虑铁芯因涡流和磁滞效应而产生的损耗。
3)不考虑定转子的电动势、磁动势、电流、电压等电气参数的谐波。
4)电机转子的绕组没有阻尼。
4 永磁同步电机的控制策略
4.1 空间电压矢量控制
交流调速的本质是需要给所控制的电动机提供电压和电流可变的三相电流,通常实现三相电流任意改变频率的装置是逆变器。“电力电子技术”课程中讲述过,逆变器可以将直流电流在经过开关器件组成的逆变装置后变为交变电流。根据逆变器的中间直流环节的应用区间不同可以将逆变器分为电压型和电流型两种,其中电压型的逆变器较为多见。
4.2 直接转矩控制
该项控制技术是利用坐标变换把永磁同步电机等效成为普通的直流电机,从而降低了控制永磁同步电动机的复杂程度,这个算法属于间接控制技术的一种,与矢量控制不同,直接转矩控制的相关方法是直接参与到电机电磁转矩的控制之中的[8-9]。
直接转矩控制的相关技术比矢量控制技术开发得晚一些,早期主要应用于异步电机控制领域,电机的电磁转矩主要由电机定子的磁链幅值大小,电机转子的磁链幅值大小和电机定子与转子磁链之间的空间夹角决定[10]。如果定子和转子的磁链幅值能保持恒定不变,那么只是改变两个磁链矢量之间的夹角,就可以实现电机电磁转矩的控制。在永磁同步电机中,转子的旋转速度与气隙中旋转磁场的旋转速度相同,转差率这个物理量在同步电机中不存在。因此,如果将直接转矩控制的相关技术引入到永磁同步电机的控制中,就需要再引入其他的物理量——同步电机的负载角[11]。
5 结论
本文首先阐述了永磁同步电机的结构,并在此基础上分析了永磁同步电机的数学模型、建模方法和控制策略,同时推导了坐标变换理论,证明了如果想调节负载角的大小,可通过让电机的定子磁链变化来实现。而如果想改变电机定子的定子磁链大小,可以利用空间电压矢量原理来实现。与基于PWM调制的空间电压矢量调制方法相似,直接转矩控制的控制策略是将空间电压矢量平均划分为六个扇区,在其应用过程中,定子磁链的幅值大小需要保持不变,此时改变空间电压矢量的控制信号则必将使得定子磁链发生改变,因此,考虑定子磁链变化时的空间电压矢量是必须的。

