爆炸荷载下钢筋混凝土面板动力响应本构模型分析
刘晓蓬,陈健云,周晶,段绪义,徐强
爆炸荷载下钢筋混凝土面板动力响应本构模型分析
刘晓蓬1,陈健云2,周晶3,段绪义4,徐强2
1. 山东农业大学 水利土木工程学院, 山东 泰安 271018 2. 大连理工大学 建设工程学部工程抗震研究所, 辽宁 大连 116024 3. 泰山职业技术学院 建筑工程系, 山东 泰安 271000 4. 山东省青州市住房保障中心, 山东 青州 262500
混凝土是建设工程中的一种主要建筑材料,采用数值方法模拟混凝土结构在爆炸荷载下的动力响应是一种新的趋势。本论文介绍了K&C模型、脆性损伤模型、JH模型和RHT模型的本构特征,并在考虑混凝土的应变率效应和动力放大因数基础上,基于LS-DYNA软件,分别数值模拟计算了钢筋混凝土面板在0.31 kg和0.46 kg的TNT炸药产生的爆炸荷载下的动力响应情况。将数值模拟结果与现场试验结果进行对比分析,结果表明:无论是从纵向、环向和散射裂纹方面,还是从中心位移和层裂区半径方面进行比较,RHT模型的钢筋混凝土面板数值模拟结果与现场试验结果最为相似,最能反映钢筋混凝土面板在爆炸荷载下的动力响应情况。
爆炸荷载; 钢筋混凝土; 本构模型
混凝土是各类建设工程中最主要的一种建筑材料,然而很多大型混凝土建筑结构由于其自身具有重要的战略意义和经济效益,比如核电站厂房、混凝土大坝和大跨度桥梁,已经越来越成为恐怖袭击和现代战争中的首选打击目标,所以研究混凝土结构在爆炸冲击下的动力响应和破坏模式就显得尤为重要。鉴于真实试验的巨大花费,以及安全性和可操作性等方面的考虑,加之随着现代计算机技术和模拟计算能力的大幅度提高,应用数值模型模拟爆炸荷载下混凝土结构的动力响应及破坏模式已经越来越得到科研人员的认可。
爆炸荷载下混凝土结构的动力响应是一个极为复杂的瞬变过程,这是因为炸药在爆炸过程中,其本身的物理和能量变化以及混凝土的材料非线性、相互间的接触非线性都使得其模拟过程变得比较复杂。同时,混凝土的力学性能还受到高加载速率和大变形的影响,在爆炸荷载下,这种影响表现得比较突出。
爆炸荷载引起的结构物损伤模式和动力响应在诸多的研究领域越来越受到人们的重视。同时有一些非线性有限元模拟软件已经能够实现结构在爆炸冲击荷载下的非线性响应过程,例如LS-DYNA和AUTODYN等。近些年,一些研究人员围绕钢筋混凝土面板在爆炸荷载下的动力响应做了相关的数值模拟研究。Pan YG等研究了考虑加劲肋影响的简单加筋板模型在不同爆炸荷载条件和应力状态下的动力响应特点[1]。Low HY等根据混凝土最大应力极限状态和位移延性能力建立功能函数,研究了钢筋混凝土面板在爆炸荷载下的可靠性问题[2]。陈万祥等通过试验研究了钢筋类型、配筋率、爆炸荷载峰值因素对高强钢筋加强混凝土板破坏形态、跨中位移、加速度及钢筋应变的影响[3]。Zhou XQ等在改进的DP损伤模型基础上,利用AUTODYN程序研究了混凝土板的动力响应及损伤预测[4]。周立江等利用ANSYS软件对钢筋混凝土面板在气云爆炸情况下的毁伤情况进行了研究,以剩余承载力为毁伤控制指标并基于超压-冲量毁伤准则绘制了不同毁伤程度的钢筋混凝土面板P-I曲线,并在数学计算基础上拟合了该钢筋混凝土面板的毁伤曲面公式[5]。Nam JW等利用高应变率敏感的材料模型和剥离破坏模型进行数值模拟,研究了钢筋混凝土面板和玻璃纤维聚合物混凝土板在爆炸荷载下的动力响应和损伤模式[6]。李忠献等研究了在爆炸荷载下典型钢筋混凝土面板的响应和破坏,提出了钢筋混凝土面板基于跨中截面剩余受弯承载力的破坏指标和数值方法计算步骤,基于数值模拟结果拟合出了该钢筋混凝土面板的P-I曲线数学表达式[7]。Tai YS等在研究爆炸冲击波传播过程的基础上,利用LS-DYNA中的JH模型研究了爆炸荷载下混凝土板的动力响应过程[8]。Lin X等综合性的研究了受不同配筋率、炸药量、板厚和爆距、网格尺寸和应变率影响时,钢筋混凝土面板在爆炸荷载下的动力响应情况[9]。高琴等对不同强度等级钢筋混凝板在爆炸荷载下的动态响应进行了数值模拟与试验结果的对比研究,并得出了在特定范围内钢筋混凝土面板的抗爆能力随混凝土强度等级增大而提高的结论[10]。Alok D等进行了接触爆炸荷载下普通混凝土板和钢筋混凝土面板的动力响应研究实验,通过建立有限元模型研究了炸药质量、板厚、混凝土强度、配筋率和配筋间距对模拟结果的影响,并基于数值模拟结果提出了相应的经验方程[11]。还有一些学者利用LS-DYNA等非线性有限元程序的RHT材料模型,对钢筋混凝土和超高韧性混凝土单向板和双向板抗爆性能和损伤模式做了研究[12-16]。以往研究应用了几种能够反映混凝土爆炸荷载下应变率相关性等性能的材料模型[17],但是目前针对各材料模型模拟混凝土在爆炸荷载下的动力响应和损伤效果的适用性问题,尚缺少明确的评判。
本文介绍了四种常用的混凝土本构模型,其分别为混凝土损伤模型(K&C模型)、脆性断裂模型、JH模型和RHT模型,并将四种模型模拟的钢筋混凝土面板在爆炸荷载下的动力响应和损伤效果与现场试验的结果进行对比,以此来进行有对比的综合判定,找出模拟混凝土爆炸响应的最合适的本构模型。
1 钢筋和混凝土的本构模型
在LS-DYNA非线性有限元程序中,提供了多种可以模拟混凝土动力响应的本构模型,但是各种本构模型表示的混凝土状态方程、应变速率和损伤状态以及不同本构模型模拟的钢筋混凝土面板在爆炸荷载下的动力响应过程和破坏状态等存在较大的差异,所以有必要对其进行专门的比较研究。本节集中介绍混凝土和钢筋的应变率相关性,能够模拟混凝土动力响应和破坏状态的K&C模型、脆性断裂模型、JH模型、RHT模型,以及钢筋的本构模型,为本文的模型验证提供理论支持。
1.1 钢筋和混凝土的应变率相关性
本文是基于钢筋混凝土面板在爆炸荷载下动力响应试验进行的数值模拟计算,研究混凝土和钢筋在动力情况下的强度特性必不可少。当应变速率达到10~1000 s-1甚至更高时,钢筋和混凝土都能够表现出比较强的应变率相关性,其最直接的表现是钢筋和混凝土的强度明显增加。在高应变率下,混凝土的抗压强度能够提高1倍,而抗拉强度能够提高6倍,钢筋的抗拉抗压强度能够提高50%左右[18-20]。
对于混凝土而言,其动力提高因子(DIF)是指混凝土的动力强度与静力强度的比值。
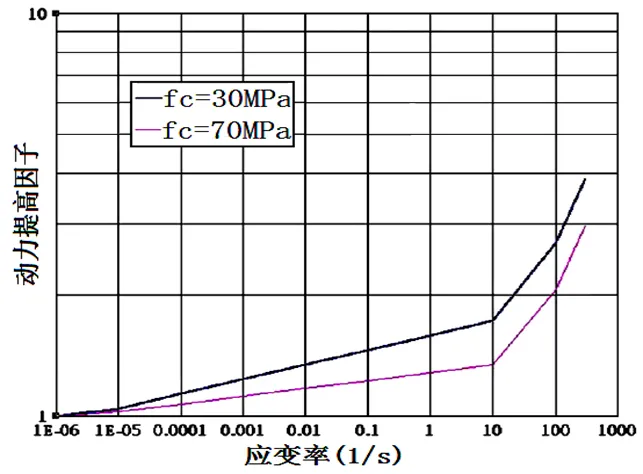
图 1 混凝土抗压强度DIF[19]

图 2 混凝土抗拉强度DIF[19]
对比图1和图2可以看出,对于混凝土而言,在相同的应变速率条件下,其抗拉强度的动力提高效果比抗压强度的动力提高效果要明显得多。在K&C模型、脆性断裂模型和RHT模型中,混凝土的抗拉强度和抗压强度分别采用了不同的动力提高因数,但是在JH模型中,混凝土的抗拉强度和抗压强度则是采用了相同的动力提高因数。
对于钢筋而言,其抗拉强度和抗压强度的DIF具有相同的取值,具体如图3所示。

图 3 钢筋的抗拉强度和抗压强度DIF[20]
1.2 混凝土本构模型
1.2.1 K&C模型K&C模型在LS-DYNA中对应的材料类型为*MAT_CONCRETE_DAMAGE,即72#材料,其本构关系可以用初始屈服面、最大损伤面和残余强度面进行描述,三者之间为相互独立的关系。
*MAT_CONCRETE_DAMAGE_REL3材料本构模型是LS-DYNA中对72#材料的改进和发展,也被称为72R3#材料。此种本构模型乃是利用三个剪切失效面来具体描述混凝土的弹塑性本构关系,同时还兼顾考虑了混凝土损伤和应变率的影响。在LS-DYNA中,可以根据实验测定的混凝土无侧限抗压强度自动生成72R3#本构模型的材料参数。

图 4 压力-体积应变曲线
72R3#混凝土本构模型的压力-体积曲线如图4所示。从中可以看出,当应力在拉应力极限值与压应力弹性极限之间时,材料呈线弹性状态;当拉应力值超过了拉应力极限值,混凝土将出现拉应力损伤;当体积应变超过了混凝土的弹性极限,混凝土将被逐渐压碎;体积弹性模量的卸载过程是一个关于体积应变最大值的函数,其可以沿着体积卸载曲线在任何阶段进行卸载,直至应力达到拉应力极限值;重新加载时,其加载曲线沿着卸载曲线回到卸载开始处,之后沿着加载曲线继续进行加载。
对偏应力张量而言,通常采用由三条强度曲线组成的混凝土强度模型来描述其变化过程,其分别为最大强度曲线,初始强度曲线和残余强度曲线,三条曲线之间相互独立,互不影响,具体如图5所示。

图 5 混凝土强度模型
1.2.2 脆性断裂模型在LS-DYNA中,*MAT_BRITTLE_DAMAGE(96#材料)本构通常被称为脆性断裂模型,其能够用三个损伤面来具体描述弥散裂缝的各向异性混凝土损伤退化过程。对于混凝土结构,如果拉伸开裂成为其主要的破坏模式,则脆性断裂模型的适用性相对较强。为了能够有效描述混凝土的压缩破坏过程,脆性断裂模型采用偏应力张量中的第二不变量对本构方程进行了简单校正。对于混凝土遭受爆炸荷载而言,由于高压应力区的存在,脆性断裂模型对于剪应力强度提高过程的描述尚有所欠缺。
1.2.3 JH模型*MAT_JOHNSON_HOLMQUIST_CONCRETE本构对应LS-DYNA中的111#材料,通常被称为JH模型。JH模型不但能够准确反映出高应变率与大变形对混凝土动力响应的影响,而且还考虑了混凝土的损伤与软化过程,对于模拟混凝土在爆炸荷载下的损伤状态效果较佳[21]。JH模型由等效强度与损伤累计两部分共同组成,在混凝土未出现损伤前,将其视为线弹性材料。其中等效强度部分的函数表达式是以混凝土的损伤和应变率及静水压力作用为变量;损伤累积部分的表达式是一个考虑静水压力、等效塑性应变和塑性体积应变等变量影响的逐渐累积积分函数。
1.2.4 RHT模型*MAT_RHT本构对应LS-DYNA中的272#材料,通常被称为RHT模型。RHT模型通过引入失效面来描述混凝土的失效强度,引入弹性极限面来描述混凝土的初始屈服强度,引入残余面来描述混凝土的残余强度。混凝土的应变硬化、软化和高应变率、大应变、高压强效应及偏应力张量的第三不变量都作为RHT模型的重要影响因素被充分考虑并设有专门参数[22]。RHT模型的失效面、弹性极限面和残余失效面如图6所示。
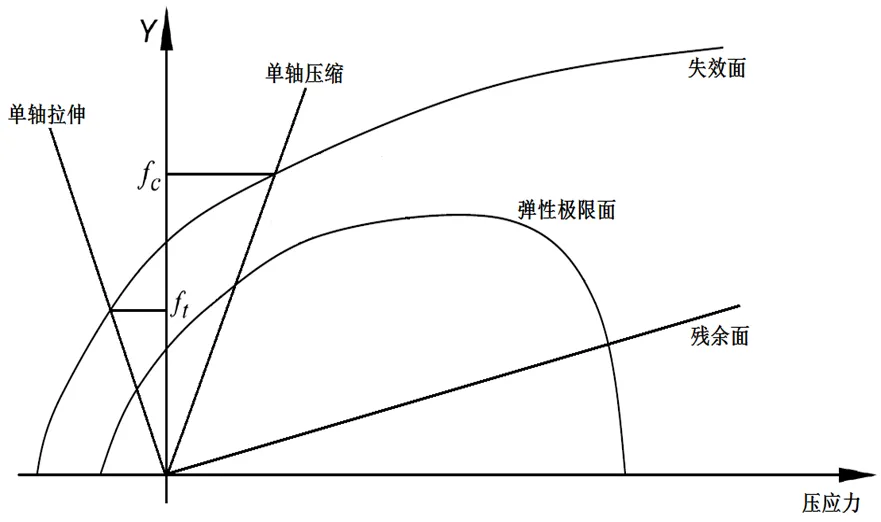
图 6 RHT模型极限面[22]
RHT模型所描述的混凝土性能衰减受到应变率效应的影响,其损伤累积过程与JH模型基本相同,但损伤因子中未将塑性体积应变考虑在内。
1.3 钢筋的本构模型

表 1 钢筋的材料参数
2 钢筋混凝土面板抗爆试验与数值模拟
2.1 试验模型
关于爆炸荷载下钢筋混凝土面板的动力响应和损伤情况,目前已经有一些学者做了相关方面的试验研究,并得出了一系列值得参考的研究结论。本文中,利用参考文献[23]中介绍的钢筋混凝土面板抗爆性能试验进行结果对比。试验所采用的是正方形钢筋混凝土面板,其边长为1000 mm,厚度为40 mm,直径为6 mm的纵向和横向钢筋均匀布置于板厚度方向的正中间,钢筋的水平间距为75mm,则配筋率为1.43%。将钢筋混凝土面板两条相互平行的边进行固定端约束,试验中炸药中心点的位置为高度方向距离钢筋混凝土面板上表面中心的400 mm处,具体如图7所示。该试验中所用钢筋混凝土面板内部钢筋网的尺寸和布置如图8所示。
该试验所用混凝土的弹性模量为28.3 GPa,抗压强度为39.5 MPa,抗拉强度为4.2 MPa。试验所用钢筋的剪切模量为81.8 GPa,弹性模量为200 GPa,屈服强度为600 MPa,密度为7.83×103kg/m3。
为了增强数值模拟的准确性和可信度,分别对TNT炸药当量为0.31 kg和0.46 kg的两组钢筋混凝土面板抗爆性能试验进行模拟[23]。

图 7 试验现场布置情况[23]

图 8 混凝土板内部钢筋网布置
2.2 数值模型
随着计算机运算能力的不断增强,以及数值模拟软件的迅速发展,利用计算机进行钢筋混凝土面板在爆炸荷载下动力响应和破坏模式的数值模拟研究已经可以实现并被众多研究学者所接受。本文的研究严格按照前述的现场试验条件,利用LS-DYNA建立该钢筋混凝土面板的3D数值仿真有限元模型,并将由K&C模型、脆性断裂模型、JH模型和RHT模型数值仿真模拟的钢筋混凝土面板动力响应和损伤情况与试验结果进行对比,以此验证数值模拟的精确性和可行性,并找出模拟效果最好的混凝土本构模型[24]。

图 9 钢筋混凝土面板尺寸及炸药布置
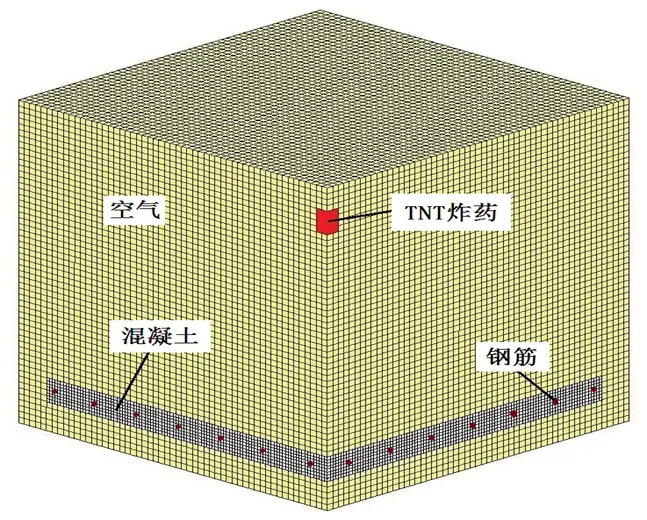
图 10 有限元模型
该钢筋混凝土面板尺寸和炸药布置的数值模型如图9所示,钢筋混凝土面板、空气和炸药的有限单元模型如图10所示,对钢筋混凝土面板、空气、炸药进行流固耦合,其中炸药和空气采用的是Euler网格划分方式,网格尺寸为10 mm,而混凝土和钢筋采用的则是Lagrange网格划分方式,网格尺寸为5 mm,在空气域的外边界处采用透射边界进行处理,使爆炸冲击波能量在外边界处完全透射而不发生反弹,以此来模拟无限空气域,并保证计算的准确性。
在LS-DYNA中,通常采用JWL状态方程来描述TNT炸药的爆轰压力,其表达式为:
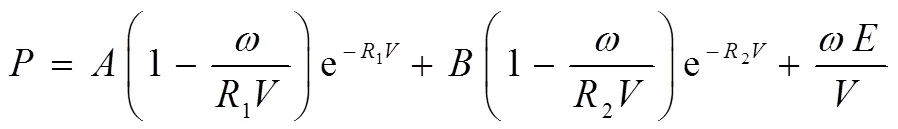

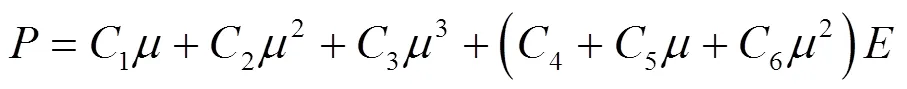
在数值模拟中,需要对混凝土设置材料参数,RHT模型中需要手动输入的参数最多(表2)。

表 2 RHT模型的材料参数[14]
3 数值模拟结果与现场试验结果的对比分析
本文中,将由K&C模型、脆性断裂模型、JH模型和RHT模型数值仿真模拟的钢筋混凝土面板动力响应和损伤情况与试验结果进行对比,以此分析四种本构模型对模拟爆炸荷载下混凝土力学性能的适用性。
3.1 TNT炸药为0.31 kg情况
在0.31 kg的TNT炸药产生的爆炸荷载下,该钢筋混凝土面板迎爆面和背爆面破坏模式的试验结果和数值结果分别如图11和图12所示。

图 11 0.31 kg的TNT爆炸荷载下钢筋混凝土面板迎爆面损伤结果
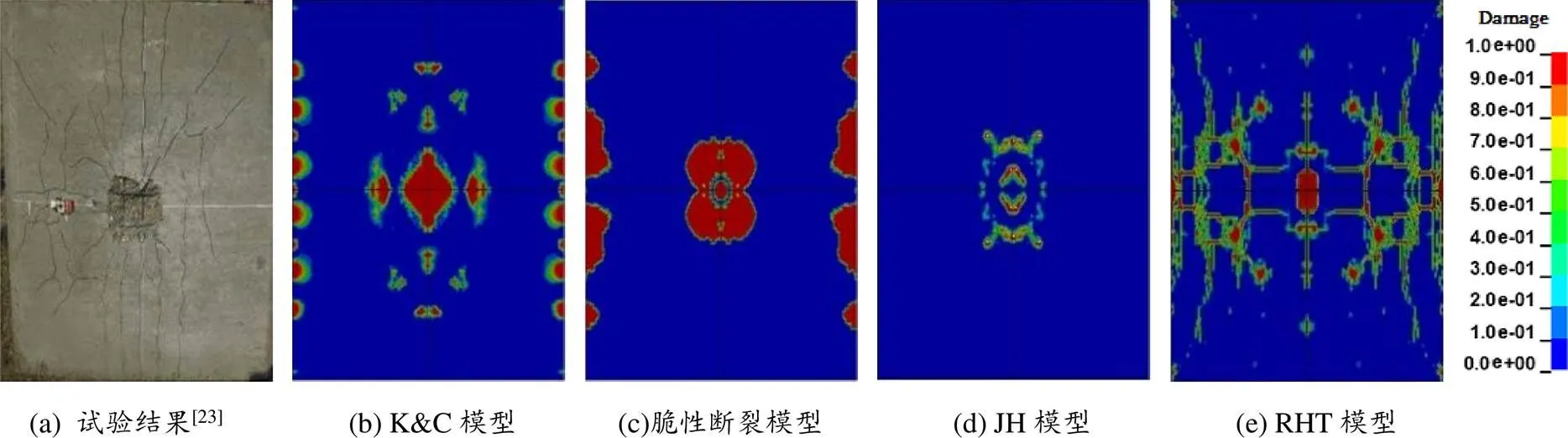
图 12 0.31 kg的TNT爆炸荷载下钢筋混凝土面板背爆面损伤结果
通过观察图11(a)可以看出,在0.31 kg的TNT炸药爆炸荷载现场试验中,钢筋混凝土面板的迎爆面中部出现了两条贯穿于整个面板且与固定约束边界平行的纵向裂纹,以及半径约为280 mm的环向裂纹和4条沿对角线走向的散射裂纹。通过观察图12(a)可以看出,在钢筋混凝土面板的背爆面中心区域形成了半径约为90 mm的混凝土脱落区(层裂区),而且背爆面存在沿钢筋走向的平行裂纹和沿对角线走向的散射裂纹。
通过观察图11(b)和图12(b)中K&C模型数值模拟结果可以看出,数值结果中钢筋混凝土面板的层裂区半径大约为100 mm,比现场试验结果大10 mm左右,但是K&C模型没有模拟出钢筋混凝土面板中裂纹的走向和扩展情况。通过观察图11(c)和图12(c)中脆性断裂模型数值模拟结果可以看出,数值结果中钢筋混凝土面板的层裂区半径约为110 mm,比试验结果大20 mm左右,而且在钢筋混凝土面板的固定约束边界处出现了与现场试验相差较大的穿透性损伤。通过观察图11(d)和图12(d)中JH模型数值模拟结果可以看出,数值结果中钢筋混凝土面板的层裂区半径约为70 mm,比试验结果小20 mm左右,混凝土的损伤呈点状分布在整个迎爆面,即使在面板中心部位的损伤也相对微弱,未出现贯穿性的混凝土脱落损伤,且没有模拟出钢筋混凝土面板中裂纹的走向和扩展情况,钢筋混凝土面板背爆面的损伤区域与现场试验相比也明显偏小。通过观察图11(e)和图12(e)中RHT模型数值模拟结果可以看出,数值结果中钢筋混凝土面板的层裂区半径约为95 mm,比试验结果大5 mm左右。RHT模型模拟的钢筋混凝土面板迎爆面裂纹走向与现场试验结果极为相似,既存在贯穿于整个面板且与固定约束边界平行的纵向裂纹,又存在环向裂纹,而且还存在沿对角线走向的散射裂纹,钢筋混凝土面板背爆面的损伤模拟与试验结果相比,未全部模拟出纵向裂纹的扩展情况。
为增加数值模拟结果与现场试验结果对比的可信度,钢筋混凝土面板的中心位移也是值得关注的要点。将数值模拟结果与现场试验结果的中心位移和层裂区半径进行对比,具体如表3所示。
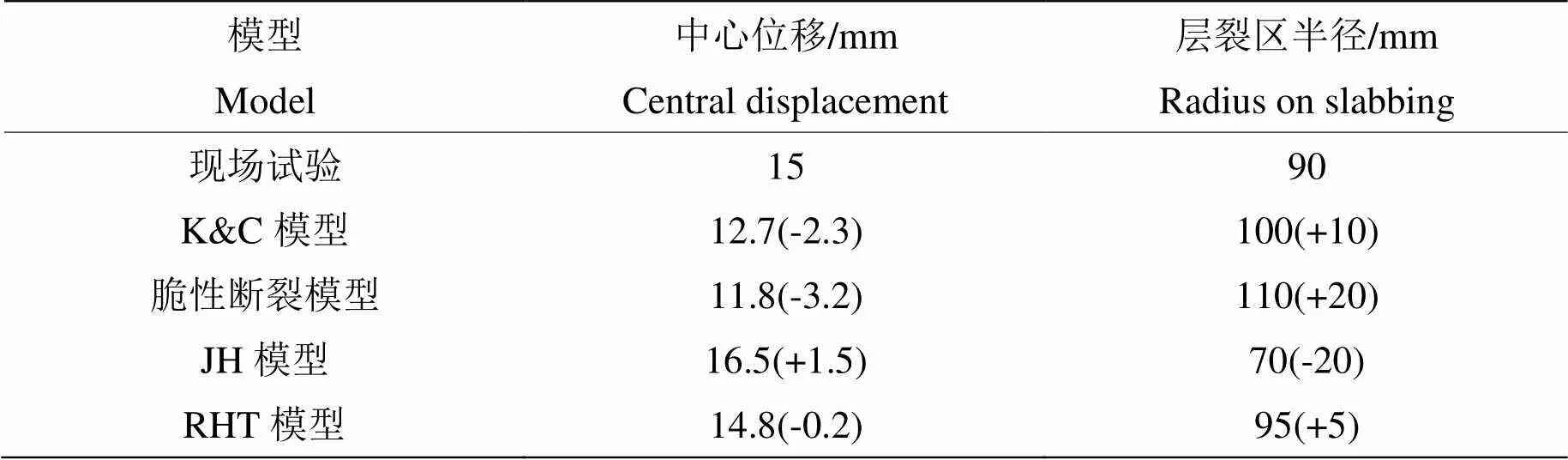
表 3 TNT炸药为0.31 kg的数值结果与试验结果对比
通过表3可以看出,从中心位移和层裂区半径的角度进行对比,RHT模型的钢筋混凝土面板数值模拟结果与现场试验结果最为接近。
3.2 TNT炸药为0.46 kg情况
在0.46 kg的TNT炸药爆炸荷载下,该钢筋混凝土面板迎爆面和背爆面破坏模式的试验结果和数值结果分别如图13和图14所示。
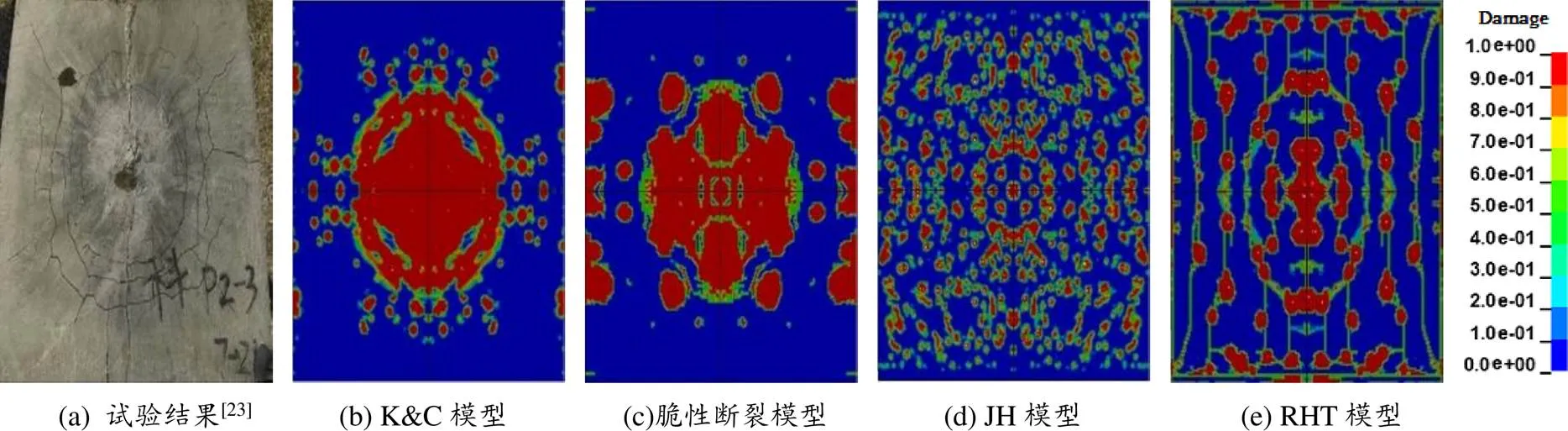
图 13 0.46 kg的TNT爆炸荷载下钢筋混凝土面板迎爆面损伤结果
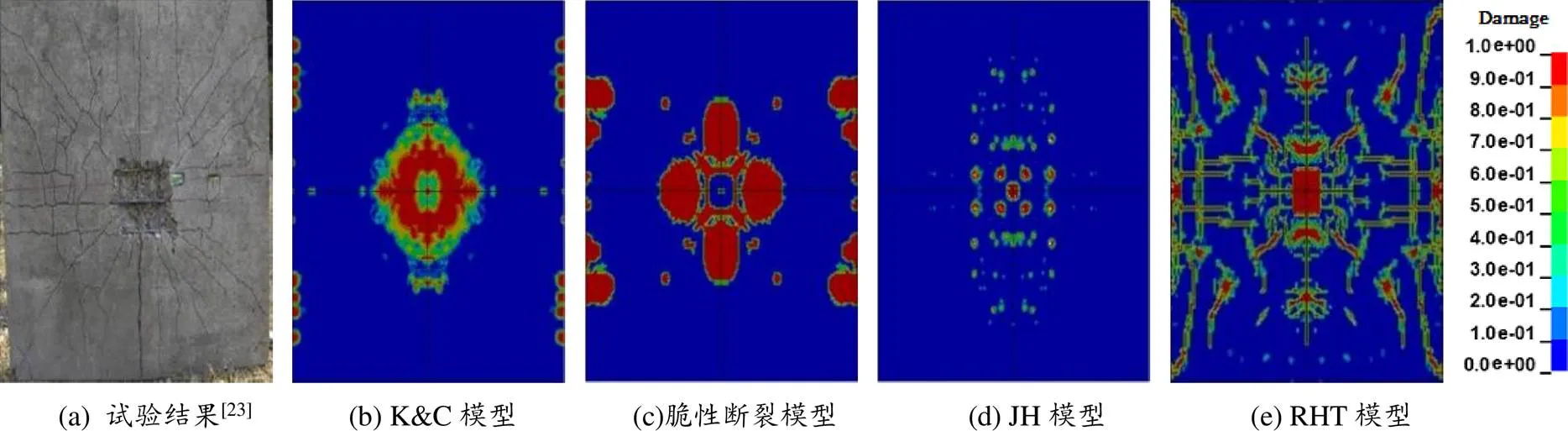
图 14 0.46 kg的TNT爆炸荷载下钢筋混凝土面板背爆面损伤结果
通过观察图13(a)和图14(a)可以看出,在0.46 kg的TNT炸药爆炸荷载现场试验中,钢筋混凝土面板的迎爆面损伤范围与0.31 kg的TNT炸药情况相比明显扩大,裂纹深度明显加深,环向裂纹的半径扩大到约300 mm,沿对角线走向的散射裂纹扩展到面板边界处,且环向裂缝周围有多条平行于固定约束边界的纵向裂纹;钢筋混凝土面板的背爆面出现半径约为120 mm的混凝土脱落区域(层裂区),且存在平行于钢筋走向和散射状的裂纹。
通过观察图13(b)和图14(b)中K&C模型数值模拟结果可以看出,数值结果中钢筋混凝土面板的层裂区半径大约为130 mm,比现场试验结果大10 mm左右,钢筋混凝土面板中裂纹的走向和扩展情况未能在数值模拟中体现。通过观察图13(c)和图14(c)中脆性断裂模型数值模拟结果可以看出,数值结果中钢筋混凝土面板的层裂区半径约为140 mm,比试验结果大20 mm左右,在面板的固定约束边界处出现了穿透性损伤,钢筋混凝土面板中裂纹的走向和扩展情况未能在数值模拟中体现,与试验结果相差较大。通过观察图13(d)和图14(d)中JH模型数值模拟结果可以看出,数值结果中钢筋混凝土面板的层裂区半径约为110 mm,比试验结果小10 mm左右,混凝土的损伤散布在整个迎爆面,且未出现贯穿性损伤,背爆面损伤区域与现场试验相比明显偏小。通过观察图13(e)和图14(e)中RHT模型数值模拟结果可以看出,数值结果中钢筋混凝土面板的层裂区半径约为125 mm,比试验结果大5 mm左右。从纵向、环向和散射裂纹方面进行对比,RHT模型数值模拟结果与试验结果极为相似[25]。
将数值模拟结果与现场试验结果的中心位移和层裂区半径进行对比,如表4所示。
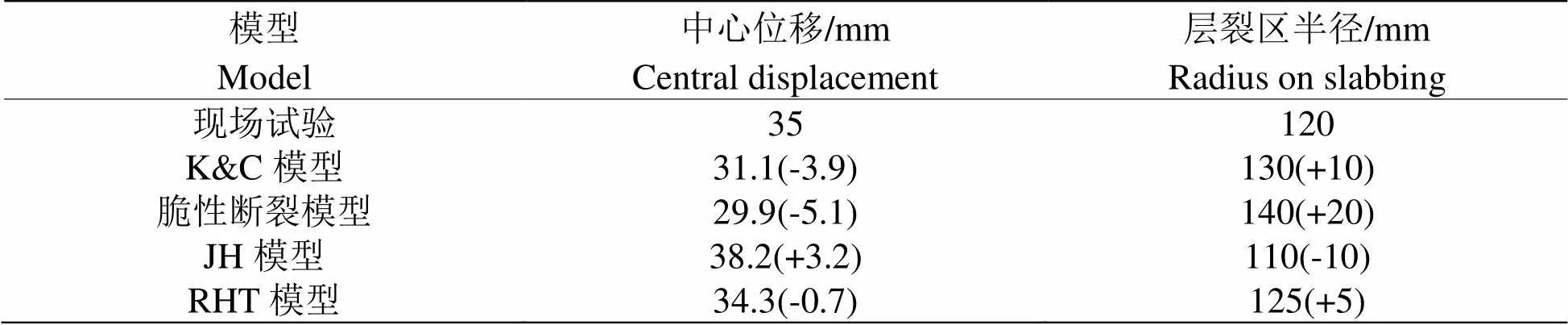
表 4 TNT炸药为0.46 kg的数值结果与试验结果对比
通过表4可以看出,从中心位移和层裂区半径的角度进行对比,RHT模型的钢筋混凝土面板数值模拟结果与现场试验结果最为相似。
综合图11至图14可以看出,RHT模型模拟的钢筋混凝土面板在0.31 kg和0.46 kg的TNT炸药爆炸荷载下的层裂区半径、裂纹分布和走向情况,与试验结果更为相符。K&C模型、脆性断裂模型和JH模型虽然能一定程度上模拟出钢筋混凝土面板的破坏形态,但存在明显不足,与现场试验结果相符度不高。K&C模型不能模拟出裂纹的走向和扩展情况,脆性断裂模型得到的固定边界区域损伤过于严重且未能模拟出裂纹扩展,JH模型得到的损伤分布则是过于散乱,未形成集中连片的层裂区。
综合表3和表4可以看出,无论是从中心位移还是从层裂区半径方面进行比较,RHT模型都是最能反映钢筋混凝土面板在爆炸荷载下的动力响应情况。与试验结果进行对比,K&C模型、脆性断裂模型和RHT模型得到的中心位移结果偏小,但是层裂区半径却偏大,这主要是因为现场试验中钢筋混凝土面板是采用塞木板的方式进行固定,故钢筋混凝土面板约束端并未按照试验描述进行全约束,木板的振动及木板本身的材料属性会消耗和吸收一部分能量。在数值模拟中钢筋混凝土面板两侧则是采用全约束的方式进行固定,面板未与除空气外的任何物质相接触,故钢筋混凝土面板内能量的散发少了一条途径,钢筋混凝土面板的损伤也必然会有所增加。
3.3 原因分析
对于K&C模型,其采用了与RHT模型不同的应变率提高因数,从总体上比较,RHT模型所采用的应变率提高方法比K&C模型所采用的径向应变率提高方法更为合理。
对于脆性断裂模型,其更适用于混凝土的破坏形式以拉伸破坏为主的情况。脆性断裂模型采用偏应力张量的第二不变量来描述混凝土的抗压破坏,但是当混凝土遭受到高应变的爆炸荷载时,则显然对混凝土抗剪强度的提高情况描述不够确切。
对于JH模型,其认为混凝土抗拉强度与抗压强度的提高因数大小是相同的,这显然不能准确反映出混凝土在高应变率时的真实动力响应情况。
与K&C模型、脆性断裂模型和JH模型相比,在RHT模型中引入了相对独立的断裂强度面概念,其不受弹性极限面和残余面的干扰,且将偏应力张量的第三不变量、应变强化、混凝土应变率相关性以及静水压强考虑在内,所以能够较好模拟出混凝土的软化过程。
综合上述的分析以及本文中所研究的钢筋混凝土面板在爆炸荷载下的动力响应情况可以得出:相对于K&C模型、脆性断裂模型和JH模型,采用RHT模型进行爆炸荷载下混凝土动力响应情况的数值模拟研究得到的结果相对更为合理,故RHT模型最能反映出钢筋混凝土面板在爆炸荷载下的动力响应情况。
4 结论
本文中详细介绍了K&C模型、脆性断裂模型、JH模型和RHT模型的材料本构和特点。利用LS-DYNA程序对钢筋混凝土面板在0.31 kg和0.46 kg的TNT炸药爆炸荷载下的动力响应与损伤状态进行了数值模拟研究分析,并与试验结果进行对比。在数值模拟过程中,充分考虑了混凝土和钢筋的应变率相关性,采用任意拉格朗日-欧拉算法对钢筋混凝土面板与空气、炸药进行流固耦合。
从数值模拟结果来看,随着炸药量的增加,钢筋混凝土面板的迎爆面损伤范围明显扩大,裂纹深度明显加深,沿对角线走向的散射裂纹扩展到面板边界处,钢筋混凝土面板的背爆面半径扩大的层裂区。
将K&C模型、脆性断裂模型、JH模型和RHT模型得到的数值模拟结果与现场试验结果进行综合对比可以发现,无论是从纵向、环向和散射裂纹方面,还是从中心位移和层裂区半径方面进行比较,RHT模型的钢筋混凝土面板数值模拟结果与现场试验结果最为相似,最能反映出钢筋混凝土面板在爆炸荷载下的动力响应情况。
[1] Pan YG, Louca LA. Experimental and numerical studies on the response of stiffened plates subjected to gas explosions[J]. Journal of Constructional Steel Research, 1999,52(2):171-193
[2] Low HY, Hao H. Reliability analysis of reinforced concrete slabs under explosive loading[J]. Structural Safety, 2001,23(2):157-178
[3] 陈万祥,卢红标,候小伟,等.高强钢筋加强混凝土板抗爆性能试验研究[J].振动与冲击,2015,34(10):135-141
[4] Zhou XQ, Kuznetsov VA, Hao H,. Numerical prediction of concrete slab response to blast loading[J].International Journal of Impact Engineering, 2008,35(10):1186-1200
[5] 周立江,范进,丁建国.气云爆炸下钢筋混凝土板毁伤的数值分析[J].爆破,2017,34(4):143-148
[6] Nam JW, Kim HJ, Kim SB,. Numerical evaluation of the retrofit effectiveness for GFRP retrofitted concrete slab subjected to blast pressure[J]. Composite Structures, 2010,92(5):1212-1222
[7] 李忠献,师燕超,史祥生.爆炸荷载作用下钢筋混凝土板破坏评定方法[J].建筑结构学报,2009,30(6):60-66
[8] Tai YS, Chu TL, Hu HT,. Dynamic response of a reinforced concrete slab subjected to air blast load[J]. Theoretical and Applied Fracture Mechanics, 2011,56(3):140-147
[9] Lin X, Zhang YX, Hazell PJ. Modelling the response of reinforced concrete panels under blast loading[J]. Materials & Design, 2014,56(4):620-628
[10] 高琴.高强钢筋混凝土板在爆炸载荷下的动态响应研究[D].武汉:武汉科技大学,2019
[11] Alok D, Abass B. Assessment of reinforced concrete slab response to contact explosion effects[J]. Journal of Performance of Constructed Facilities,2020,34(4):04020061
[12] Wang W, Zhang D, Lu F,. Experimental study and numerical simulation of the damage mode of a square reinforced concrete slab under close-in explosion[J]. Engineering Failure Analysis, 2013,27(1):41-51
[13] 汪维,张舵,卢芳云,等.方形钢筋混凝土板的近场抗爆性能[J].爆炸与冲击,2012,32(3):251-258
[14] Zhao CF, Chen JY. Damage mechanism and mode of square reinforced concrete slab subjected to blast loading[J]. Theoretical and Applied Fracture Mechanics, 2013,63-64(1):54-62
[15] Li J, Hao H. Numerical study of concrete spall damage to blast loads[J]. International Journal of Impact Engineering, 2014,68(3):41-55
[16] Mohamed AK. Modified settings of concrete parameters in RHT model for predicting the response of concrete panels to impact[J]. International Journal of Impact Engineering, 2019, 132:103312
[17] Bischoff PH, Perry SH. Compressive behaviour of concrete at high strain rates[J]. Materials and Structures, 1991,24(6):425-450
[18] 周清,齐麟.LS-DYNA软件中5种常用抗爆混凝土材料模型的分析与比较[J].混凝土,2019(11):43-49
[19] Malvar LJ, Ross CA. Review of strain rate effects for concrete in tension[J]. Materials Journal, 1998,95(6):735-739
[20] Malvar LJ. Review of static and dynamic properties of steel reinforcing bars[J]. ACI Materials Journal, 1998,95(5):609-616
[21] Holmquist TJ, Johnson GR. A computational constitutive model for glass subjected to large strains, high strain rates and high pressures[J]. Journal of Applied Mechanics, 2011,78(5):051003
[22] Tu Z, Lu Y. Evaluation of typical concrete material models used in hydrocodes for high dynamic response simulations [J]. International Journal of Impact Engineering, 2009,36(1):132-146
[23] Wang W, Zhang D, Lu F,. Experimental study on scaling the explosion resistance of a one-way square reinforced concrete slab under a close-in blast loading[J]., 2012,49(2):158-164
[24] 周清,张云海,齐麟.LS-DYNA软件中4种不同爆炸荷载施加方法的比较[J].兵器装备工程学报,2021,42(2):216-221
[25] 刘晓蓬.爆炸荷载和地震作用下混凝土坝动力破坏及防护措施研究[D].大连:大连理工大学,2018
Analysis of Constitutive Model of Dynamic Response of Reinforced Concrete Slab under Explosive Loads
LIU Xiao-peng1, CHEN Jian-yun2, ZHOU Jing3, DUAN Xu-yi4, XU Qiang2
1.271018,2.116023,3.271000,4.262500,
Concrete is the main material in construction engineering, and it is a new trend to use numerical methods to simulate the dynamic response of concrete structures under explosive loads. This paper introduces the constitutive characteristics of K&C model, brittle damage model, JH model and RHT model. Considering the strain rate effect and dynamic amplification factor of concrete, and based on the LS-DYNA software, the dynamics of reinforced concrete slab under the explosive loads of 0.31kg and 0.46kg TNT explosives are numerically simulated and calculated respectively. The comparative analysis of the numerical simulation results and the field test results shows that, whether it is from the longitudinal, circumferential and scattering cracks, or from the center displacement and spall zone radius, the numerical simulation results of the RHT model are most similar to the experimental results, and can best describe the dynamic response of reinforced concrete slab under explosive loads.
Blast loads; reinforced concrete slab; constitutive model
TU528.571
A
1000-2324(2022)04-0640-11
10.3969/j.issn.1000-2324.2022.04.022
2021-12-28
2022-02-24
国家自然科学基金(51679030);“十三五”国家重点研发专项(2017YFC0404900)
刘晓蓬(1988-),男,博士,讲师,研究方向:结构抵抗极端荷载能力研究. E-mail:liuxiaopenglw@sdau.edu.cn

