基于多机器学习模型的逐小时PM2.5浓度预测对比
陈建坤,牟凤云,张用川,田 甜,王俊秀
(重庆交通大学智慧城市学院,重庆 400074)
随着工业化进程的发展,空气污染已成为全球性公共卫生问题。在主要的大气污染物中,粗颗粒(PM10)和细颗粒(PM2.5)对空气质量、大气能见度以及全球气候变化的负面影响最严重[1-2]。已有研究表明,空气污染是造成人体多种疾病的主要环境因素[3],在全球范围内,约3%的心肺疾病和5%的肺癌与PM暴露有关[4],高PM2.5浓度与多种急性和慢性疾病密切相关[5-7]。因此,对PM2.5浓度进行预测极为重要。
当前PM2.5浓度预测方法主要有确定性模型和数据驱动模型两类[8]。确定性模型依赖于排放源数据和各类历史气象数据,通过大气污染物扩散和物质的物理化学过程模拟污染物的形成[9-10]。确定性模型运用广泛,高斯模型(AERMOD、PLUME等)、欧拉模型和化学迁移模型[11](GEOS-Chem,CMAQ,WRF-Chem等)是最常用的物理过程模型,但地形和土地利用某些方面的复杂性一定程度上限制了这些模型的应用[12]。有研究发现,传统的确定性模型难以描述污染物浓度、气象、土地利用以及排放和扩散源之间的非线性关系[13]。近年来,依托算法模型研究的不断深入和计算机硬件性能的不断提升,使得以机器学习算法为代表的数据驱动模型已成为许多学科研究的首选方法。在PM2.5预测研究领域内,郑毅等[14]和曲悦等[15]采用神经网络方法对PM2.5浓度进行模拟预测,结果表明神经网络能够较好地预测PM2.5浓度,LSTM模型预测准确率较高,但存在容易因为网络调试问题陷入局部最小化、训练时间长的问题;李建新等[16]和宋国君等[17]基于改进的支持向量机模型在一定程度上能提高PM2.5浓度的预测精度;康俊锋等[18]在预测PM2.5浓度时构建了6个机器学习模型,从不同方面对比分析了模型的预测性能。
综上所述,基于机器学习模型预测PM2.5浓度已有不少研究成果,但大都聚焦于单一算法模型或对模型的简单改进,较少涉及多个算法模型的对比分析。此外,在预测模型的输入特征变量选择方面,较多研究选择与PM2.5直接相关的空气污染数据或者只选用气象数据,结合两者来预测PM2.5浓度的研究鲜见报道。但气象因子对PM2.5浓度变化影响较大[19],因此,本研究尝试使用空气污染监测数据和气象监测数据构建基于机器学习的PM2.5预测模型。由于多个特征之间存在信息冗余,需要对10个监测指标进行降维处理。已有学者使用相关系数法[20]和主成分分析[21]进行特征子集选择,但相关系数法要求各个特征相互独立,主成分分析方法主要适用于线性问题,而监测指标之间通常存在非线性关系[22],笔者采用最大相关最小冗余算法(MRMR)选择最优特征[23],并构建XGBoost模型、随机森林模型(RF)、LightGBM模型、K最近邻模型(KNN)、决策树模型(DT)、长短期记忆神经网络(LSTM)6种机器学习模型,进行PM2.5浓度预测。
1 材料与方法
1.1 数据预处理
采用重庆市合川区(105°58′37″~106°40′37″E,29°51′02″~30°22′24″N)7个空气质量监测站点的空气质量监测小时数据(PM10、SO2、NO2、CO、O3)和气象因子监测数据(气温、湿度、风速、风向、气压)对大气PM2.5浓度进行预测。所有数据均为站点监测小时数据,每个站点每天产生24条数据(表1所示为2020年1月23日逐小时监测数据);研究数据覆盖的时间范围为2020年1月18日至2021年1月30日。

表1 站点逐小时监测数据样本
数据采集过程中由于监测设备和其他外界因素的影响,监测数据中存在部分缺失数据和异常数据,需要对原始数据进行数据预处理操作,控制数据质量。具体包括:①剔除气象站点监测历史数据中的异常值和缺失值,且如果监测数据中的某一项值为缺失或者异常,则该小时所有数据全部剔除。②在剔除原始数据异常值的同时,对PM2.5质量浓度(浓度)小于0 μg/m3和大于1 000 μg/m3的异常数据也进行剔除处理。③通过数据质量控制后,最终选用数据共62 780条。采用train_test_split随机划分数据集。测试数据集占比设置为20%。另外,特征缩放可以消除各维数据之间的量级差别,提升分类算法和优化算法的性能。特征缩放的主要方法有归一化和标准化,其中,标准差标准化方法使得特征值呈正态分布,利于训练阶段的权重更新;同时标准化方法还可以保持异常值的信息,进一步减少异常值对算法的影响。在机器学习模型训练之前对样本数据(x)进行标准差标准化,公式如下:
(1)
式中:x*为标准化数据,μ为所有样本数据的均值,σ为样本数据的标准差。
1.2 预测模型及参数选择
1.2.1 6种模型的特征
选取的6个机器学习模型及最终确定的模型参数如表2所示。
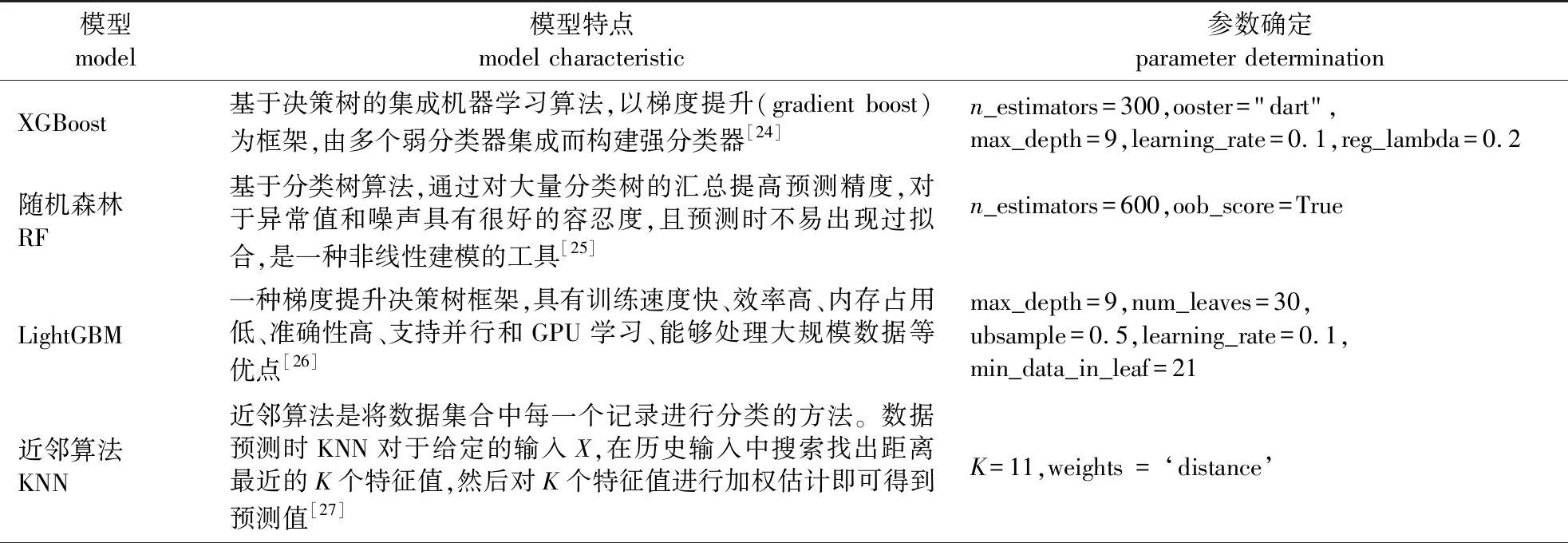
表2 6个预测模型及其参数确定

表2(续)
1.2.2 基于互信息的最大相关最小冗余算法(MRMR)的最优特征选择
考虑到PM2.5浓度与各个影响因素之间为非线性关系[22],且变量之间存在较强的相关性,对多个监测指标必须考虑其数据之间的冗余性。因此本研究引入了基于互信息的最大相关最小冗余算法(MRMR)[30]选择最优特征,该算法可以最大化特征与目标变量之间的相关性,同时最小化特征之间的相关性。给定的两个随机变量X与Y之间的互信息定义为:
(2)
式中:p(X)和p(Y)分别是X和Y的概率密度函数;p(X,Y)为X与Y的联合概率密度函数。
令Ω=Ωs∪Ωt表示整个特征集,其中Ωs表示m个已选择的特征,而Ωt包含n个待选择的特征。可以通过以下公式计算特征f(以Ωt为单位)与目标c的相关性D:
D=I(f,c)。
(3)
此外,以Ωt为单位的特征f和所有以Ωs为单位的特征冗余度R可以通过以下公式计算:
(4)
结合上式可以给出具有最大相关性和最小冗余度的以Ωt为单位的特征fj:
(5)
对于具有N个特征的特征集,特征排名将连续N个回合。在对特征进行排名之后,将通过MRMR方法获得新的特征集S:
(6)
本研究基于10个特征维度的数据,计算出了PM2.5浓度与10个特征之间的互信息值(表3)。互信息的大小表明了特征之间的相关性强弱,最优特征子集选择时既要考虑特征之间相关性强弱,也要考虑冗余度的大小。经MRMR算法选取出的最优特征子集包括:PM10、NO2、O3浓度和气温、风向、气压,即以选取的6个特征作为模型的输入。CO和湿度与PM2.5相关性较高,但并没有入选最优特征子集,这印证了MRMR算法确实考虑了特征之间的冗余信息,从而选取最优的特征子集。

表3 PM2.5浓度与特征之间互信息
1.3 模型评价方法
采用决定系数R2、均方差RMSE(式中记为σRMSE,下同)、平均绝对误差MAE(σMAE)、平均绝对百分比误差MAPE(σMAPE) 4个指标[31]对模型进行评估,评价指标的计算方法如下:
(7)
(8)
(9)
(10)
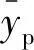
2 结果与分析
2.1 6种模型的PM2.5浓度预测结果及精度比较
6种模型使用同样的训练集与测试集,用训练数据集测试模型,再将测试数据集输入模型进行PM2.5浓度的预测,预测值与实测值的对比情况如图1所示。
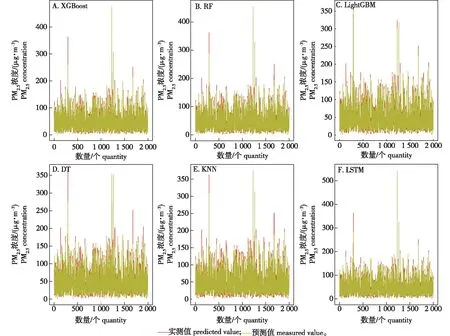
图1 PM2.5浓度的预测结果与实测结果Fig.1 Predicted and measured results of PM2.5 concentration
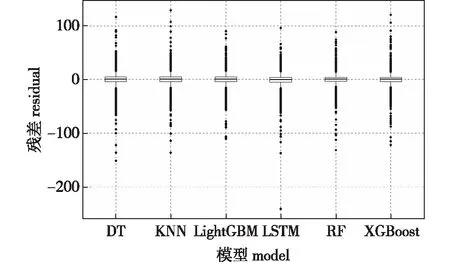
图2 预测模型残差Fig.2 Prediction model residual
结合预测结果与实测结果对比图(图1)以及各模型预测残差图(图2)可知:当PM2.5浓度处于20~70 μg/m3时,各模型的预测精度较高,预测值与实测值重合度高;当PM2.5浓度大于100 μg/m3时,模型预测值与实测值差异变大;当PM2.5浓度持续增大超过150 μg/m3后,预测值与实测值之间的差异较大,预测效果不理想。总体而言,当PM2.5浓度实测值较小或过大时,模型预测值与真实值之间相差较大。XGBoost、RF、LightGBM、LSTM模型的预测效果优于DT和KNN模型,其预测值与真实值更接近,LSTM模型对于实测值较大的数据预测效果更好。
基于PM2.5浓度实测值与模型预测值,做出6个预测模型的回归散点图(图3),并计算实测值与预测值的R2、RMSE、MAE、MAPE等指标。总体而言,6个机器学习模型均有R2>0.92,这表明选择的最优特征子集能较好地预测PM2.5浓度。其中XGBoost、RF、LightGBM 等3个模型的R2>0.94,DT、KNN、LSTM模型的R2在0.922~0.937之间;各模型的RMSE处于8.168~9.543之间,XGBoost模型的RMSE最小、DT模型的RMSE值最大为9.543。对比MAE,则DT模型的MAE值最大,值为6.168,其余5个模型的MAE值均小于6;最小值为XGBoost 模型的5.218,其次为RF模型的5.376和LightGBM模型的5.62。比较MAPE指标,则XGBoost模型的仍是所有模型中最小,为16.669%,其次为RF模型的16.684%,整体而言所有模型的MAPE值均小于20%,其中KNN模型的最大,为19.056%。综合对比6个机器学习模型,XGBoost模型的预测性能最好,其次是RF和LightGBM模型,DT模型的预测性能相对较差。
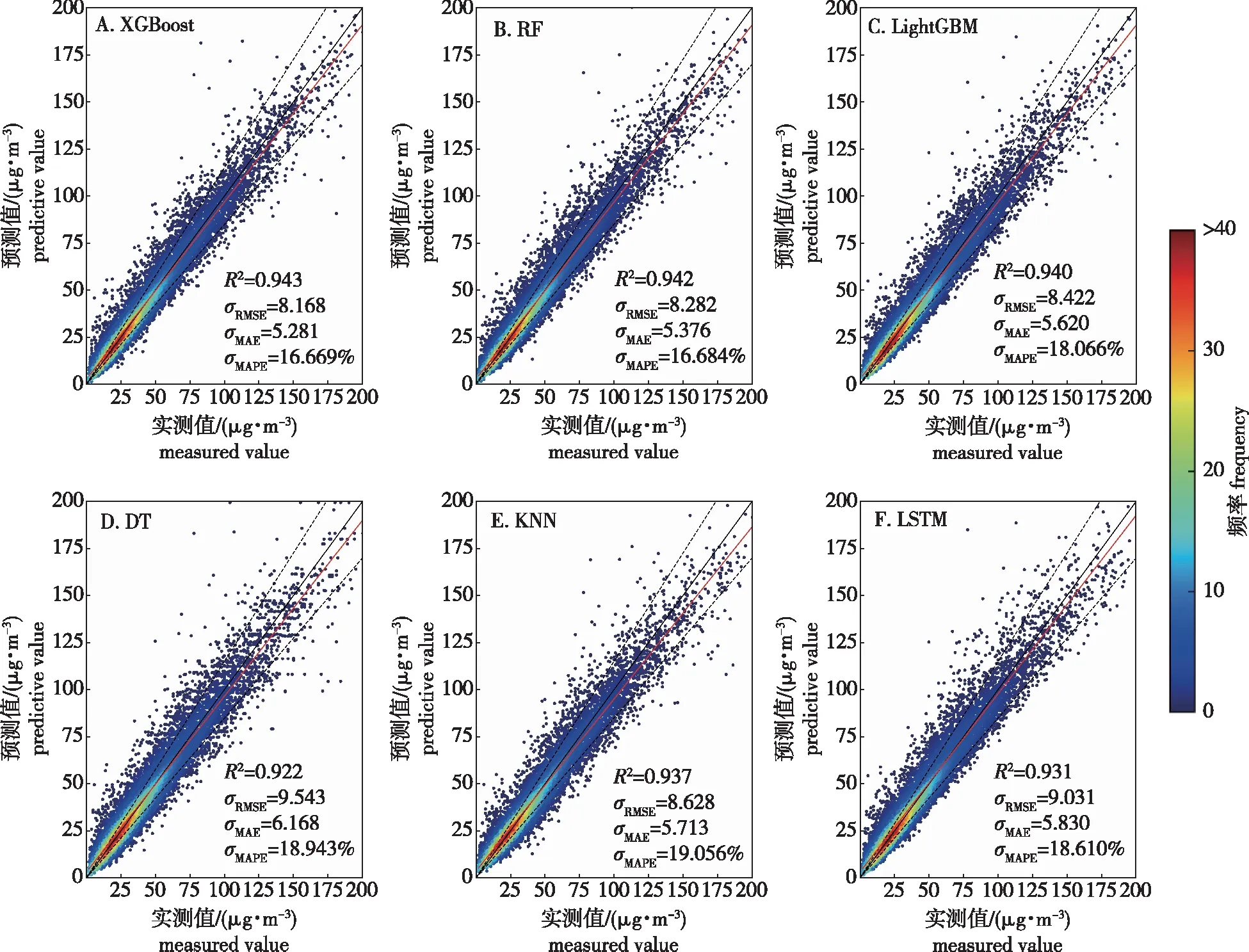
图3 6种模型预测回归对比Fig.3 Comparison of six models for prediction and regression
2.2 6种模型预测等级分析
根据国家环境保护标准空气质量指数规范[32],对研究区(合川区)PM2.5浓度实测数据和模型预测数据进行等级划分(表4)。从实测数据看,合川区污染等级主要集中在1~4级,重度污染(5级)和严重污染等级(6级)数量相对较少。从各模型预测结果看,KNN模型1级污染数据数量最多,其次为RF模型,最少的是LSTM模型,是6个模型中1级预测数据量唯一少于实测值的模型;2级污染数据中,LSTM模型数量最多,KNN模型数量最少。总体上各模型预测等级数量与实测值数量相差较小。
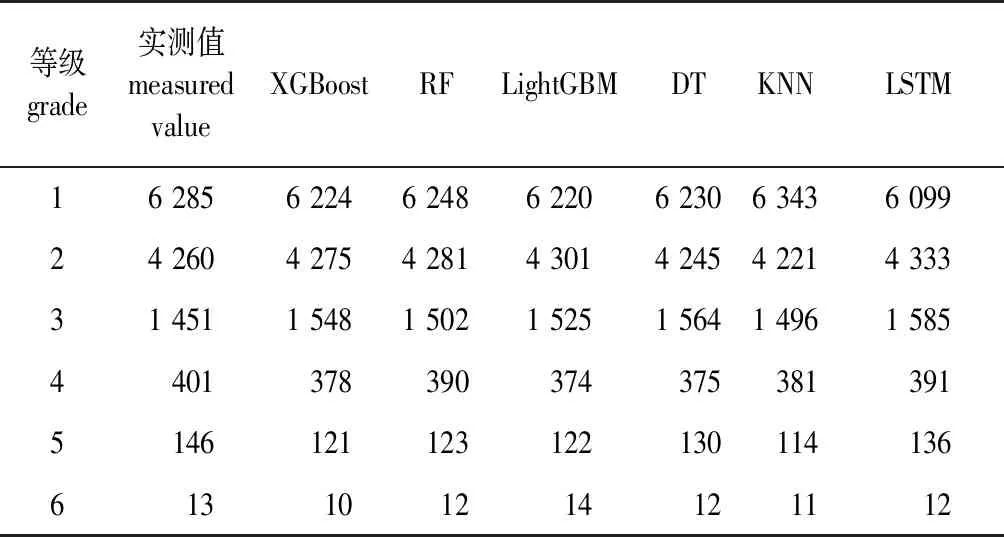
表4 6种模型对合川区PM2.5污染等级预测对比
2.3 不同季节各模型预测精度的对比分析
考虑到不同季节空气污染物来源差异[33],且重庆市四季气候变化大,不同的气候条件下气象因子也会对PM2.5浓度产生影响,因此以季节为监测时间单位,探究不同季节下(季节划分为:3—5月为春季,6—8月为夏季,9—11月为秋季,12月至次年2月为冬季[34])各模型的预测性能差异,结果见表5。
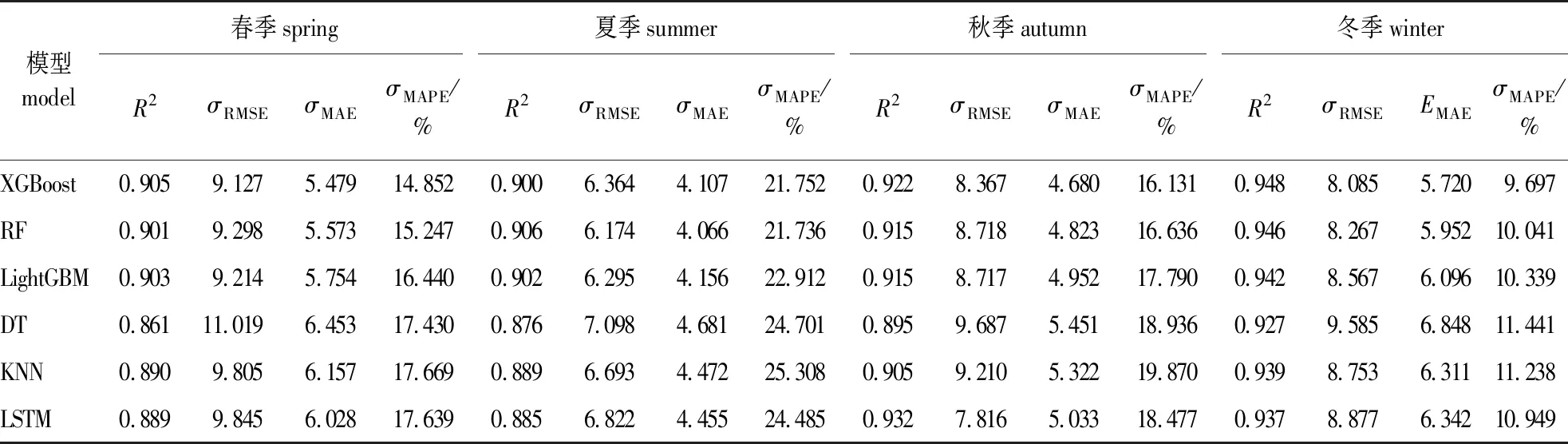
表5 不同季节各模型预测结果
由表5可知,6个模型对PM2.5浓度预测整体上呈现秋季和冬季预测结果更好,春季和夏季预测结果较差。结合重庆合川区PM2.5浓度季节性变化看,秋冬季节PM2.5浓度高于春夏季节,这说明模型在污染等级较高时预测值更稳定,性能更好。对比模型预测精度,DT模型预测结果较差,R2在春季、夏季、秋季均小于0.9,其春季预测结果是所有预测结果中最差的(R2=0.861,RMSE为11.019,MAE为6.453,MAPE为17.430%)。XGBoost模型预测结果最好,R2在4个季节均大于0.9,其冬季MAPE值仅为9.7%,是所有模型中唯一小于10%的。整体而言,XGBoost、LightGBM、RF模型预测结果优于其他3个模型,在不同季节预测结果中R2均大于0.9,XGBoost模型预测性能略优于其余两个模型。LSTM模型预测效果稍逊于3个集成学习模型,但明显优于KNN和DT模型。预测结果的差异可能与机器学习模型算法的内部特性有关,还可能与不同季节下污染物和气象因子的变化有关。为了进一步探讨模型在不同季节下预测结果差异性的原因,分析了PM2.5浓度与特征变量之间的相关性,结果如图4所示。
PM10浓度是4个季节中与PM2.5浓度相关性最大的变量,相关性在4个季节中基本保持不变。NO2在夏季相关性小于其他3个季节;O3与PM2.5浓度呈负相关,且夏季相关性最小;气温与PM2.5浓度呈负相关,且呈现出春夏季节相关性大于秋冬季节;风向与PM2.5浓度相关性最小,在春季表现为负相关,其他3个季节为正相关;气压在春季与PM2.5浓度相关性最强,且呈负相关,而在其他3个季节呈正相关。对比分析可知秋冬季节气象因子与PM2.5浓度相关性明显小于春夏季节,这种相关性的变化会影响预测模型季节性预测的误差。
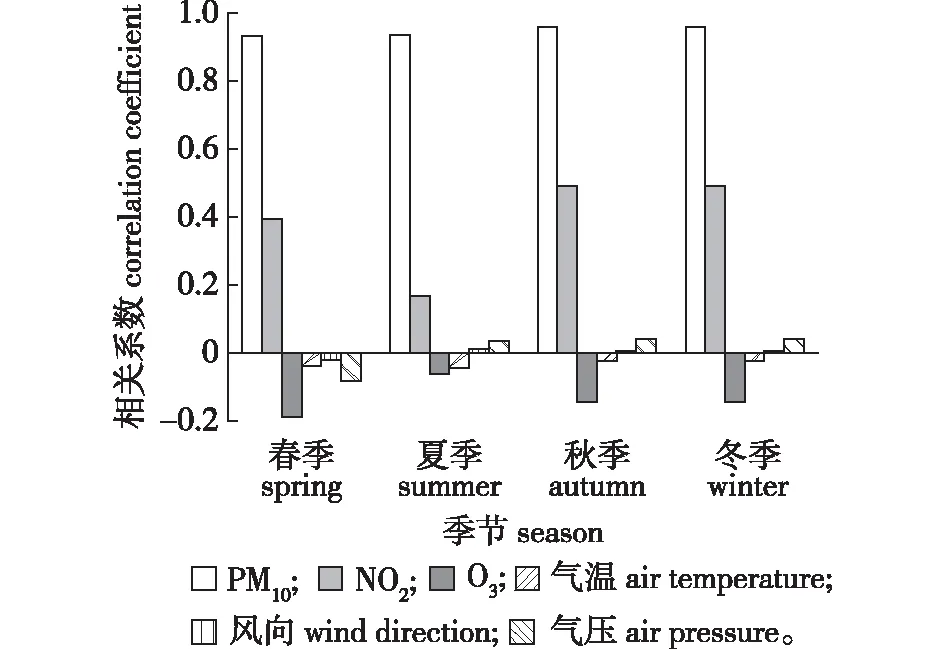
图4 各季节下PM2.5浓度与特征变量的相关性Fig.4 Correlation between PM2.5 and characteristic variables
2.4 6种模型运行效率及特征变量重要性比较
模型构建完成后,计算各模型运行时间和内存占用大小,结果见表6。如表6所示,RF模型是所有模型中内存占用最大且运行时间最长的模型,DT模型是所有模型中内存占用最小的,其运行时间也最少,其余模型在内存占用大小上相差不大;LSTM模型运行时间为46.5 s仅次于RF模型,但远小于RF运行时间。结合模型预测性能对比分析可知:LightGBM模型和XGBoost模型预测性能相差不大,但LightGBM模型在内存占用大小和运行时间上都能减少,LightGBM模型在运行时间上相较XGBoost模型减少了一半,这也证实LightGBM可在保证预测精度的条件下,减少内存占用和运行时间。
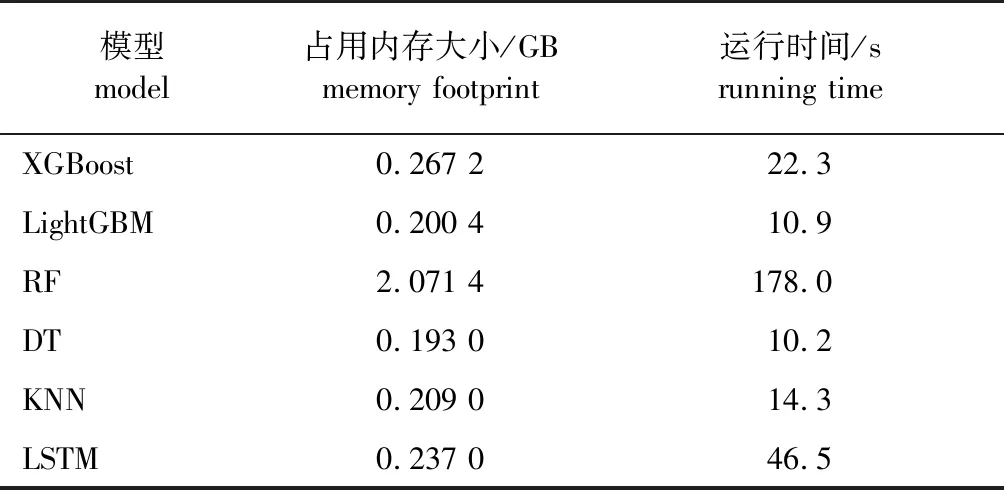
表6 模型内存占用大小和运行时间
综上可知,XGBoost、RF、LightGBM模型在PM2.5浓度预测中表现出了较好的性能,对保存好的模型进行变量重要性分析,各个特征变量相对重要性如图5所示,XGBoost模型和RF模型中特征变量相对重要性顺序一致,重要性顺序为PM10浓度、气温、气压、O3、风向、NO2。LightGBM模型中NO2重要性略大于风向,其他变量相对重要性与其余两个模型一致,可以看出PM10浓度、气温、气压对于PM2.5浓度预测较为重要,O3、风向、NO2对于PM2.5浓度预测重要性相对较弱。
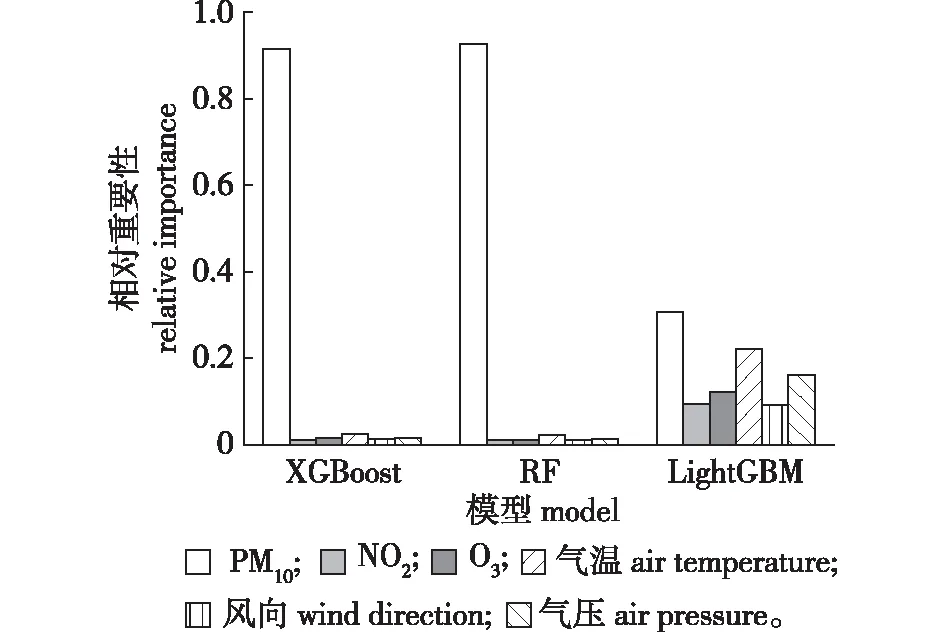
图5 特征变量重要性Fig.5 Importance of feature variables
3 讨 论
本研究以重庆市合川区为研究区,结合空气污染数据和气象监测数据基于最大相关最小冗余算法(MRMR)选取最优特征子集,选择6个机器学习模型进行PM2.5含量预测,对比分析了各模型的预测性能,包括模型预测的总体精度、不同季节条件下的预测能力、模型运行效率等。结果认为:基于MRMR算法选取的最优特征子集作为模型输入可以很好地预测PM2.5浓度,预测结果较理想。6种模型预测性能整体较好,3种树模型预测性最好,LSTM模型次之,DT模型最差。对比不同季节下各模型预测结果发现,6个机器学习模型在秋冬季节污染物含量较高的情况下,预测性能优于春夏季节。分析各季节下PM2.5浓度与各特征变量之间的相关性可知,秋冬季节气象因子与PM2.5浓度相关性明显小于春夏季节,这是导致模型不同季节预测性能差异的原因。对比各模型的运行时间和内存占比发现,RF模型内存占用和运行时间最大,DT模型运行时间和内存占用均最小。另外,XGBoost、RF、LightGBM模型中各个特征变量的相对重要性顺序基本一致,即PM10浓度、气温、气压重要性高,O3、风向、NO2重要性相对较弱。相较于XGBoost模型,LightGBM模型可以在保证性能的条件下大幅缩短模型运行时间。
采用MRMR算法对研究区(合川区)全年数据进行数据降维,进而构建多机器学习模型对PM2.5浓度预测。实验证明,该方法能取得较好的预测精度,可以为环境部门进行PM2.5浓度短时精确预测和PM2.5浓度预警提供参考,但研究还有进一步提升的空间:气象数据(气温、湿度、风速、风向、气压)为站点逐小时监测数据,没有选用能见度数据,一方面是由于监测站点并未采集到对应时刻的能见度数据;另一方面考虑到其他渠道获取的能见度数据在时间和空间上并不能完美契合该时刻的其他数据。当然如果能获取对应的能见度数据,可以考虑作为输入特征进行进一步实验。另外,本研究未深入探讨PM2.5浓度变化与气象要素和污染数据变化之间的内在联系,未对其他特征子集预测效果进行试验,今后的研究可以尝试补充其他合适的特征变量进行预测。在模型构建方面,本研究主要进行多模型预测对比分析,今后可以致力于模型改进与多模型融合,进一步提高模型的预测性能。

