基于鲁棒优化的保险资金投资组合模型*
张 梦 媛
(北京邮电大学理学院,北京 100876)
0 引 言
现代保险公司披露的利润表显示其利润主要来源于保费收入和投资收益.保险业发展日益成熟,保险公司承保业务遇到瓶颈,其利润不断下降;疫情爆发经济下行,公司原保费收入增速同比明显减缓,而保险资金运用余额增速未受影响.因此,投资业务逐渐成为支撑保险公司持续发展的重要业务.此外,保险资金投资渠道和投资比例进一步放开,为保险资金运用创造了更好的发展环境.
保险资金指保险公司在日常经营工作中所能用的各类资金总和,主要包括资本金(保险公司的开业资金)和保险业务的准备金等.保险公司可以利用暂时闲置的资金进行投资,从而实现资金的保值增值,这种经济活动即为保险资金投资,或为保险资金运用.与其他投资一样,保险资金投资遵循安全性、盈利性和流动性3个原则,然而保险行业的特殊性还决定了其自身独特的投资特点.如保险公司要保证发生事故和灾害时能对客户进行足额偿付,所以为保障资金的安全性,需要限制保险资金投资风险资产的比例.
由以上分析知,在中国银行保险监督管理委员会(简称银保监会)监管要求下,保险公司有必要制定合理高效的保险资金投资组合,从而能更好地抵御风险,提高收益来保障偿付能力.Cramer[1]最早开始研究保险资金组合;Markowitz[2]首次建立了均值方差模型,并界定了理性投资者的概念;Lobo等[3]考虑到投资组合中的参数不确定性问题,提出了用鲁棒优化方法解决;Nemirovski和 Ben-Tal[4]综述了鲁棒优化在不确定线性规划和二次曲线规划中的主要应用结果;Ben-Tal和 Ghaoui[5]介绍了鲁棒优化基本模型的构建以及涉及到的概念;Reddy[6]认为保险公司面临的投资风险与投资收益成正相关,即投资风险越大,投资收益越高;Bertsimas和 Sim[7]提出将一般圆锥规划转化成鲁棒对等的方法,可以保证鲁 棒解的可行性;Quaranta 和 Zaffaroni[8]用鲁棒优化技术代替随机规划来处理不确定性,以此最小化股票投资组合的条件风险值;Olivares-Nadal和DeMiguel[9]证明数据驱动的投资组合问题在收益和交易成本之间可达到最优平衡;许仨[10]采用效用函数和在险价值等因素,建立了保险投资最优模型;赵庆[11]综述了鲁棒优化在不同投资组合模型中的应用;刘小东[12]基于均值方差模型的保险资金投资组合,进行了实证研究;高莹等[13]结合线性矩阵不等式和鲁棒优化方法,解决了均值方差模型结果容易因参数变动而变得不可行的问题;安晓敏[14]建立了势不确定集下的鲁棒投资组合决策模型.受现有研究启发,本文利用已有的均值方差模型和鲁棒优化方法,致力于构建基于鲁棒优化的保险资金投资组合模型,并选取近几年保险投资数据进行实证分析,确认鲁棒优化在投资组合中是否具有良好性质.
1 基于均值方差模型的保险投资组合策略
1.1 假设条件与模型构建
早在 1952年,美国著名经济学家 Markowitz[2]提出只用收益(均值)和风险(方差)2个变量就能研究投资组合问题,由此建立了均值方差模型,模型基本假设条件为:投资收益水平可以用期望收益率衡量;投资风险水平通过收益率的方差度量;理性投资者行为具有“风险规避性”和“追求收益性”,即投资者在收益既定时选择风险最小组合,在风险既定时选择收益最大组合;投资组合杜绝卖空现象,即组合中各类资产比例非负.在基本假设条件下,建立保险资金投资组合模型的假设如下:

假设2 据银保监会规定,保险资金投资各类资产的金额受一定比例限制,设为 αi≤ wi≤ βi,i=1,2,…,n.
假设3 各类资产的收益率向量和标准差向量均 为 常 值 ,分 别 表 示 为 R=(r1,r2,…,rn)′和 Ω =(σ1,σ2,…,σn)′,则投资组合收益率 rp为各类投资资产收益率的加权平均值,即

用投资的n种资产收益率的协方差矩阵C来表示投资组合的风险水平,即

式中 :C=cov(ri,rj)= σiσjρij,ρij是ri和rj的相关系数.
假设4 投资者进行理性投资,在达到最低预期收益前提下要求风险最小.
基于均值方差模型的基本条件和上述假设1~4,可以建立如下保险资金投资组合的均值方差模型,模型目标是满足最低预期收益率时最小化投资风险:
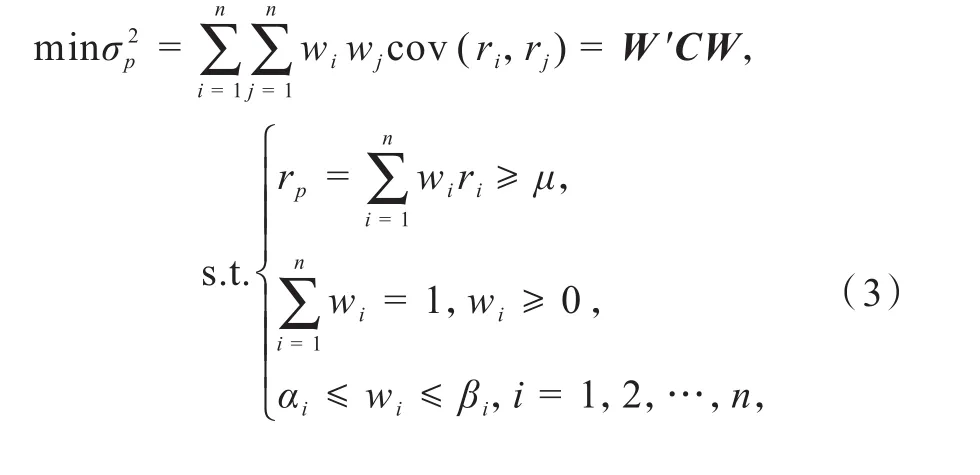
式中:αi和βi分别代表银保监会规定的投资第i类资产权重的下限和上限;第一个约束条件代表保险公司的预期收益率最低为μ.
1.2 实证分析与模型求解
1.2.1 样本数据选择
根据2018年银保监会发布的《保险资金运用管理办法》[15],保险资金运用限于银行存款、债券、股票、基金、不动产和境外投资等形式.因此,本文选取以上6种形式来配置保险资金投资组合,选择2015年1月1日—2019年12月31日作为研究区间,相应的研究数据主要有银行存款利率、债券收益率、股票回报率、基金收益率、不动产和境外投资收益率,数据来源于中国人民银行网站、中证指数有限公司官网和恒生指数有限公司官网.本文认为保险公司投资银行存款无风险,而债券、股票、基金、不动产和境外投资均有风险,以下按投资是否有风险分类确定所投资的各项资产收益率.
(1)无风险资产收益率.保险资金投资的银行存款主要包括定期存款和活期存款,因此,选取1年定期存款利率和活期存款利率,以二者的平均值当作无风险资产收益率.由中国人民银行网站公布的利率数据可知,2015—2019年活期存款利率均为0.003 5,1年定期存款利率均为0.015 0,取二者均值可得无风险资产收益率为0.009 3.
(2)风险资产收益率.对于债券、股票和基金,本文以中证全债指数、上证综合指数和上证基金指数为基准来分别计算各自收益率.首先,利用对数差分算出月收益率为

式中:Mt代表各指数在t月的收益率,Pt表示各指数在t月的数值.加和月收益率得到年均收益率为

对于不动产,主要指投资的土地、建筑物等,本文以地产指数为基准,计算保险资金投资此资产的收益率,方法同上.
境外投资,我国保险资金的境外投资活动主要在香港市场进行,以香港恒生指数计算境外投资收益率,方法同上.
通过上述方法,得到2015—2019年各风险资产收益率,详细列于表1.各资产投资比例限制:为防范系统风险,银保监会在2014年发布了《关于加强和改进保险资金运用比例监管的通知》,针对保险公司配置各类资产的份额进行限制:投资股票和基金的账面余额,合计不能超过本公司上季末总资产的30%;投资于不动产的账面余额不高于公司上季末总资产的30%;境外投资余额合计不高于本公司上季末总资产的15%.

表1 2015—2019年风险资产收益率
1.2.2 模型求解
由样本数据确定式(3)中,投资总资产种类n=6;r1、r2、r3、r4、r5和r6分别为银行存款、债券、股票、基金、不动产和境外投资的收益率,分别为0.009 3、0.031 5、0.023 6、0.053 9、0.278 1和 0.042 6;w1和w2为银行存款和债券的投资比例,银保监会未对其作上限要求;w3、w4、w5和w6分别为股票、基金、不动产和境外投资的投资比例,取值范围为w3+w4≤30%、w5≤ 30%、w6≤ 15%.
根据各类风险资产的收益率,计算出协方差矩阵为

将以上数据代入保险资金投资组合均值-方差模 型(3)得:

第一类投资资产银行存款为无风险资产,故目标函数中W=(w2,w3,w4,w5,w6)′.
令μ取不同值,代表公司能接受的不同最低收益率,利用MATLAB编程求解.得到满足最低收益率时,风险最小的投资组合(表2).可知,随着保险公司所能接受最低预期收益率μ增加,公司所面临的资金投资组合总风险σ2p逐渐变大,得到的收益率rp也随之增加,符合市场规律.参考此表,不同保险公司可根据自身所能接受的最低收益来制定风险最小的投资组合.
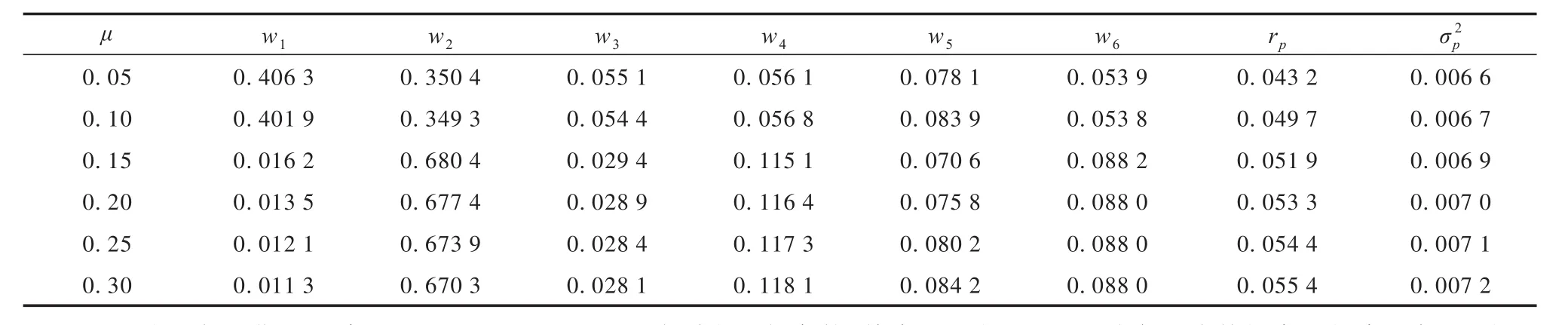
表2 满足最低收益率时的最小风险组合
保险公司在制定投资组合策略时,经常会有很多现实约束,一个重要原因是在均值方差模型中,参数比如投资组合的期望收益率和协方差矩阵通常都用统计方法估计而定,这是不准确的.因此,当参数发生一个很小的波动时,就有可能导致解变得不可行.所以,有必要对模型进行改进,找到一种有效的手段来处理参数的不确定性给投资决策带来的问题.
2 鲁棒约束下的保险投资组合模型
鲁棒优化是一种有效应对优化问题中参数不确定性的优化方法,具体而言,鲁棒优化方法是将参数的不确定性处理成能直接描述且较为简单的几何形式(如矩形和椭球形),由此把原规划问题转化成确定优化问题,使最终解在输入任何一个可能参数时,都能一定程度上达到最优.因此,可用鲁棒优化来解决上述模型中投资组合收益率不确定问题.
2.1 基于线性矩阵不等式的鲁棒优化模型
近年来,线性矩阵不等式(linear matrix inequality,LMI)已经成为构建鲁棒优化模型的一种重要方法.原因之一为MATLAB中推出的LMI工具箱[13],使得用此方法进行鲁棒优化变得更加直接、可操作性更强.因此,为解决均值方差模型中参数不确定性问题,首先将其转化为目标函数确定、约束条件为LMI的鲁棒优化模型,即

此模型中具有ζ和W这2个决策变量:W表示所投资资产组合的金额比例权重向量;ζ表示投资资产组合的最大方差,ζ=max=maxW′CW.模型的目标函数旨在求得ζ最小时的投资组合权重向量W,其经济意义是当保险公司面临市场上最大风险ζ=max时,选择合适的投资策略W,使得保险资金投资组合收益波动最小mWinζ.
式(3)~(5)的本质是目标函数和约束条件的形式转化.式(5)中约束条件①是由ζ-W′CW ≥0根据Schur补性质[14]等价变换而来;其余约束条件所表示的含义与式(3)相同.
2.2 不确定集与鲁棒对等模型


2.3 实证分析
2.3.1 鲁棒优化模型求解步骤
通过LMI解决保险资金投资组合鲁棒优化问题的具体步骤框架[16]如图1所示.第1步,确定保险公司投资能接受的μ;第2步,根据历史数据设出投资资产的收益率变动情况,给出如式(6)类型的收益率不确定集UR,并据此计算相应的协方差矩阵;第3步,根据模型用MATLAB求解,得出各投资组合的最大方差,再求出最小风险的鲁棒解;第4步,令μ取表2中所有设的μ值,重复第2和3步,由此得到具有鲁棒性的最小风险组合.

图1 基于鲁棒优化的保险资金投资组合问题框架[16]
2.3.2 仿真计算
选取2015—2019年研究区间中数据进行实证,并将实证部分中的收益率和协方差作为基准收益率R1、基准协方差C1.
据本文所选数据,一般假设无风险资产收益率不变,风险资产收益率变动幅度≤20%,故设风险资产为使结果具有代表性且方便计算,选取不确定集中收益率的下限Ra和上限Rb,其分别对应的协方差矩阵为Ca和Cb.
由上文数据可知,当收益率取Ra=0.8R1时,协方差矩阵Ca为

当收益率Rb=1.2R1时,协方差矩阵Cb为

将Ra、Rb的取值及矩阵Ca和Cb代入投资组合鲁棒优化模型,在μ取表2中所设的μ值时,求出具有鲁棒性的结果(表3).可知,随着保险公司可接受的预期收益率最低值增加,保险资金投资组合的风险增加,最终获得的组合收益也增加,仍然符合市场规律.

表3 具有鲁棒性的最小风险组合
3 结果比较与经济意义解释
为了更加直观地对比保险资金投资组合均值方差模型和鲁棒优化模型的绩效情况,当预期收益率最低值μ相同时,即保险公司进行投资活动前对投资组合的最低预期收益率相同时,2个模型投资组合实际获得的投资收益率和承受风险的比较如图2所示.在不同保险资金投资组合模型下,实际收益率随着最低预期收益率变动均呈上凸图形,见图2(a),说明在均值方差模型和鲁棒模型中,投资收益率都是随最低预期收益率先快速增长后缓慢增长,且鲁棒优化模型具有较高且稳定的收益.分析可知,此现象是由于当保险公司能接受一个较低预期收益率时,公司可能正处于发展上升期,实际收益增长迅速;而当预期收益率达到临界值,并且还在提高,说明公司发展已较为成熟,投资资金增多,面临的风险增加,投资收益总量较之前提高,但增速不如之前快.在不同保险资金投资组合模型下,承受风险随最低预期收益率变动均呈递增趋势,见图2(b),这说明不论是哪种保险资金投资组合模型,预期收益率增加时,公司需要承担的风险必然增加,符合市场规律.然而在保险公司能接受的同一最低预期收益率下,鲁棒约束的保险资金投资组合模型需要承受的风险恒小于基于均值方差的保险投资组合模型所需承受的风险,很好地体现出了鲁棒优化模型较为保守的特点,即具有相同预期收益率时,其承受的风险较小.

图2 均值方差模型与鲁棒优化模型对比(a)收益率;(b)风险
4 结束语
本文主要研究了鲁棒约束下制定保险资金投资组合策略问题.在均值方差模型的基础上,增加了保险资金投资各项资产比例的约束条件,建立了保险投资组合均值方差模型.此外考虑到模型中参数不确定性问题,运用鲁棒优化方法对模型进行了扩展,构建了鲁棒约束下的保险投资组合均值方差模型.同时选取2015—2019年的市场数据,对基本模型和扩展模型进行了实证研究,得到了相同预期收益率下各自的最优投资组合;并且比较分析了2个模型结果,表明鲁棒优化模型得到的投资组合具有更高收益且更加保守,在预期收益率相同时面临更小的风险,这为保险公司进行资金投资活动提供了新思路.

