基于粒子群算法优化极限学习机的供热管网负荷预测研究

城市供热系统的负荷预测已经有许多人提出了各种预测方法，包括基于统计模型的负荷预测以及基于诸如神经网络的机器学习算法的负荷预测。基于统计模型的负荷预测方法主要是把以气象要素为基础，这样的解决方案即包括相对简单的线性特征的处理方法，也包括更复杂的真实物理系统与综合统计学的处理方法[1-2]。有些方法以供热网络的物理知识作为基础，结合统计模型对系统参数进行辨识，其中 Box-Jenkins 方法被应用于自回归滑动平均模型（ARMA）。基于统计学模型的负荷预测还包括季节性差分自回归滑动平均模型（SARIMA），该模型通过卡尔曼滤波导出预测值[3-4]。

负荷预测的另一个主要路线是基于机器学习相关方法，如神经网络或支持向量机。这些方法在理论上可以增加解决方案处理数据中非线性和非稳态的能力，例如通过引入递归神经网络（RNN）来提高处理非稳态热需求的能力[5]。城市供热系统中有许多影响因素构成了总的热需求，并且实际上不可能做出这种需求的确切模型。正是因为这样，不需要精确的物理模型的统计模型和机器学习方法正好可以被用来解决供热系统负荷预测的问题[6]。

1 极限学习机基本原理

极限学习机是由前馈网络进行的优化和改良而成，它在监督与非监督学习问题方面显示了其高效、精确的特点[7]。极限学习机和普通的神经网络区别在于，普通神经网络应用梯度下降算法，而极限学习机可以预先设定参数值，这样就可以让给定的参数不再被后期训练过程改变，因此，该算法在整个学习过程中始终是不变的，与其他类型学习方式如单层次感知器和 Back Propagation(BP) 神经网络，在速度和泛化性能上都有明显的优越性。

目前大部分的神经网络都是通过梯度下降的学习方法来进行训练，但由于其具有不确定的学习效率，容易陷入局部最优化，从而导致了在训练时产生较大的预测误差。为了解决传统神经网络中的许多问题，极限学习机选择了不可微激活函数，并利用某些参数保持不变来减少模型的复杂性，从而使学习速度得到了明显的改善。在极限学习机训练中，根据要求预先设置了一个不确定的量，即隐藏层的结点数目，而在权值的求解中，极限学习机只求解一个广义逆矩阵，而且，在极限学习机开始训练之前，它的关键参数是随机生成的，不需要进行任何的动态调节，从而大大降低了训练的时间。极限学习机的拓扑结构如图1 所示。

图1 极限学习机拓扑结构

其最大创新点如下。

（1）输入层与隐藏层之间的链接权值和隐藏层的阈值可以任意设置，设置完成后无需进行任何的调节。算法不同于 BP 神经网络，它必须时刻逆向地调节权重和阈值，如此一来，计算的工作量就会降低一大半。

（2）在不用迭代法调节的情况下，隐藏层与输出层的连接权系数可以一次求解。

结果显示，该方法具有较好的泛化能力和较快的运算速率。

设置序列x＝[x1,x2,...,xn]T，xi∈Rn，y＝[y1,y2,...,yn]T，yi∈Rn为给定序列的标签，假定该模型具有隐藏层结点数为l，激活函数设定为g(x)，可以用如式（1）来表示极限学习机模型。

式中：ωi—激活函数的第i个权重值，i＝1,2,3,...,l，权重值具体表示为ωi＝[ωi1,ωi2,...,ωim]；

bi—激活函数的第i个阈值；

βi—极限学习机隐含层第i个节点的权重值，具体表示为：βi＝[βi1,βi2,...,βim]。

可以用式（2）表示。

式中：H—输出矩阵，由激活函数等构成。

输出层权值的具体计算公式如式（3）所示。

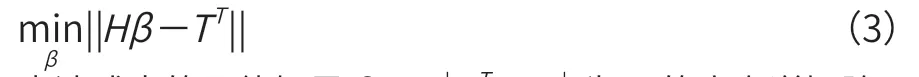
表达式中的具体解是β＝H+TT，H+为H的广义逆矩阵。

2 粒子群算法优化极限学习机（PSO-ELM）过程

粒子群优化算法(Particle Swarm Optimization, PSO)是一种基于信息分享原理的启发式优化方法[8-9]。利用资源分享原理使粒子从随意运行到有序的探索，该方法将鸟类视为理想的颗粒，故得名粒子群，采用粒子群方法建立鸟类的寻找食物行为，建立了相应的约束条件。

针对目前城镇供暖系统存在着较大的随机性和预测精度不高的问题，对其提出了一种改进极限学习机的供热系统热负荷预测方法[10-11]。

粒子群算法优化极限学习机的供热系统热负荷预测操如下。

（1）收集以往的供热系统运行负荷数据和相应的天气温度等数据，如表1 所示。

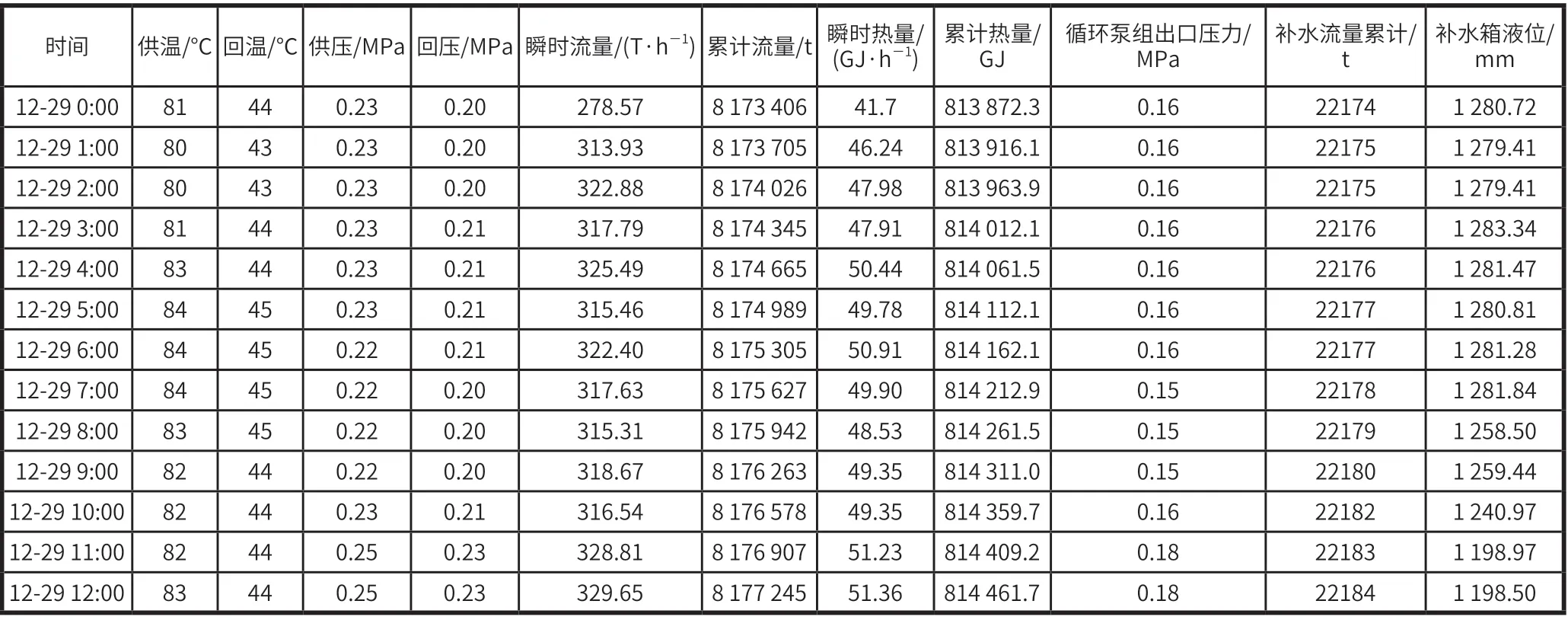
表1 供热管网实际运行数据表

利用最大最小值方法以及插值方法对数据中的异常值进行剔除和校正，并将全部数据做无量纲处理。

采用平均值内插方法填补丢失的数据，其表示如式（4）。

式中，xi—丢失数值补足后的值；

xi-1—丢失数据之前时间的原始数据值；

xi+1—丢失数据之后时间的原始数据值。

采用极大极小法对数据进行无量纲操作，其表示如式（5）。

式中：y—经过无量纲操作之后的数据；

x—原始数据顺序数；

xmin—原始数据顺序最小值；

xmax—原始数据顺序最大值。

（2）利用皮尔逊相关系数与相互信息技术，结合供热区域内的气温，管网瞬时流量、一次侧供回水温度数据作为主要影响因子，以历史热负荷数据共同作为预测模型的输入量，建立极限学习机热负荷预测模型[12]。

（3）应用 PSO 优化算法，对极限学习器的关键参数优化调节。

（4）通过对样本进行适当地分割，建立预测模型的训练集合以及测试集，并采用 PSO-ELM 算法对测验集训练，以获得合适的连接权值和阈值等至关重要参量[13-15]。

（5）运用构建的 PSO-ELM 热负荷预测模型和第四步中对重要参数优化的值，对测验数据实行预测，从而获得相关的预测数据。

（6）为了对预测的结果做出正确的评价，本文选择了三个主要的误差评价指标进行评估，并给出了相应的计算公式。

①平均绝对误差公式见式（6）。

式中：xi—预测数值；

yi—初始数值；

m—数据量。

②平均绝对百分比误差公式见式（7）。

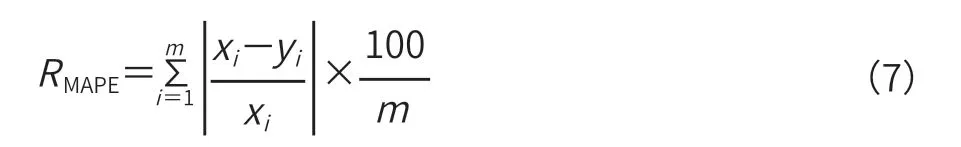
③均方根误差公式见式（8）。

基于 PSO 算法优化极限学习机的短期负荷预测具体流程如图2 所示。

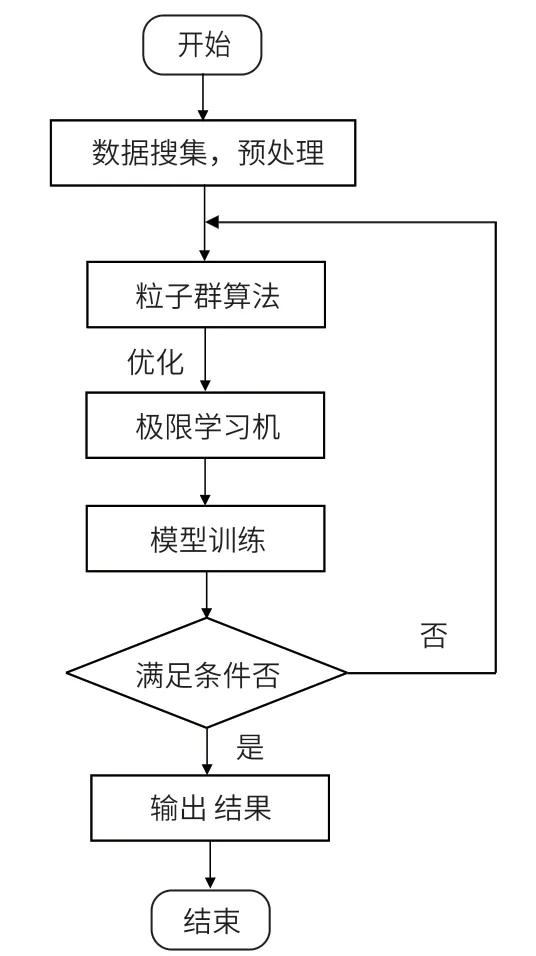
图2 PSO 算法优化极限学习机的短期负荷预测具体流程图

3 仿真试验

该部分采用 MATLAB 软件对本文所提及的机器学习方法进行计算操作，比较了各种评估指数下 BP 神经网络算法、ELM 算法和 PSO-ELM 算法的优劣。

本文以天津某换热站集中供热系统真实运行数据为基础进行预测方法比较，所涉及数据采样时间间隔为 1 h，一天共计 24 个数据并与对应时间的气象温度结合，选择了 2020 年 12 月 26-30 日 5 个供热系统正常运行的数据，将前 3 日数据做为训练数据进行供热系统热负荷预测模型的训练，其余两日则做为测验数据的预测效果。供热数据设计参数类型有一次侧回水温度、瞬时负荷、一次侧供回水流量和累计负荷。

通过仿真与其它传统预测算法比较，本文提出的预测模型曲线拟合度较高，尤其是在热负荷发生突变时刻表现得更为突出，能够较好的模拟出真实的热负荷表动情况。不同预测方法误差结果如表2 所示。

由表2 可以看出，与其它预测算法比较，PSO-ELM 的各误差评价指数明显下降。与传统的 BP 神经网络比较，该预测方法平均绝对误差下降了 0.145 01；相对于 ELM 预测方法，该方法的平均绝对误差下降 0.096 69，说明粒子群算法能较好的解决极限学习机的参数优化问题。

表2 负荷预测误差结果比较

4 结 语

本文先是简述了供暖系统热负荷预测的重要意义，并对极限学习机算法理论知识进行了简要的阐述，接着，介绍了 PSO-ELM 优化算法过程，最后应用 PSO 方法优化极限学习机进行预测模型建立，以某集中供热系统实际工况运行数据以及数据对应的气象数据作为输入进行了热负荷短期预测，提出的预测算法与其他传统预测方法结果相比，在四个主要的误差指数上都有较明显的下降。对热负荷的精准预测是实现供暖系统更加经济节能运行的基础。