多普勒雷达与L波段雷达垂直风廓线对比分析
祁凯 吴林林 张庆奎
(1 安徽省阜阳市气象局,安徽 阜阳 236000;2 安徽省人工影响天气办公室,合肥 230000)
引 言
多普勒天气雷达能够测量其探测范围内任意点相对于雷达的径向速度,通过速度方位显示(Velocity Azimuth Display,VAD)算法[1-4]可以计算出风的垂直廓线(Vertical Wind Profile,VWP),由于算法的固有误差和多普勒雷达探测的自身局限,如果少于25个数据点时或者均方根误差超过5 m·s-1时,就没有测风数据,所以VWP产品的可靠性和适用范围仍是一个值得研究的课题[5-6]。
L波段雷达通过跟踪自由上升探空气球携带的探空仪,测得每秒钟探空仪相对雷达的仰角、方位和斜距,然后根据气球在某时段内的位置变化,计算出相应大气层中的平均风向风速[7];而多普勒雷达VAD风测量的是以雷达为中心半径30 km左右的平均风[8],且时间经过一定的平滑处理,测风原理不同会使两者之间产生测风偏差。由于长期以来业务上以探空测风作为高空风的标准[9],因此依据L波段雷达测风检验与多普勒雷达VAD方法反演风之间的差距,对比分析两者测风的系统偏差。杨梅等[10]利用2002—2005年4—6月37次多普勒雷达风廓线资料与探空资料进行相关性分析,得出两者具有较好的相关性。黄祖辉等[11]以一次天气过程为例分析多普勒雷达与L波段雷达的测风误差,讨论了误差的来源。裴丽丝等[12]利用2004—2007年的天气雷达风廓线资料和利用其他探空站通过多项式插值法计算得到本地探空资料进行相关性分析。薛双青等[13]利用15个相近的雷达站与探空站2009年6月的资料进行偏差分析,得到风向偏差为23.0%,风速偏差为51.6%。以上分析的测风数据样本都较少,或通过插值计算出测风数据,也仅进行了相关性和偏差分析,对两者测风数据差异的系统性分析依然不够。本文采用2012—2017年阜阳多普勒雷达与L波段雷达风廓线资料进行相关性和误差分析,将两者测风数据在不同高度、不同天气过程、不同速度区间和不同季节的方法进行对比,分析误差原因,检验多普勒雷达与L波段雷达测风的系统性偏差。
1 测风资料的选取与匹配
1.1 多普勒雷达和L波段雷达站点选取
为了保证检验资料可靠性,站点选取尽量满足相同位置、相同时间、相同高度的原则[13]。相同位置:本研究选择的资料来源于阜阳国家高空气象观测站和阜阳多普勒雷达站,两者相距8 km,间距小于30 km。相同时间:阜阳高空站每天观测时间为07时15分(北京时,下同)和19时15分,而多普勒雷达的资料每6 min一组数据,将对比测风数据采用靠近法进行匹配时,两者在同一测风高度的时间尽量保持一致(时间差阈值后面作具体分析)。相同高度:阜阳L波段雷达天线海拔高度为44 m,阜阳多普勒雷达天线的海拔高度为67 m,高度差较小。综上所述,选取阜阳探空站和多普勒雷达站基本满足对比要求。
1.2 测风资料的匹配
通过探空业务数据处理软件导出阜阳高空气象观测站2012—2017年测风秒数据,包含全部对比高度层的测风数据和对应测风时间(精确到秒)。对阜阳S波段多普勒雷达2012—2017年VWP原始风廓线数据读取,获取在固定高度层(30层)的风向风速数据。将获取的多普勒雷达VWP数据在某一高度上(0.3~15.2 km)的风向风速与L波段雷达测得同一高度的风向风速按时间因子匹配。由于多普勒雷达数据为每6 min一组,两者同一高度的测风时间不能完全一致;测风数据匹配的规则按照时间差小于设定的阈值,从表1可以看出不同时间差匹配的数据对样本数量影响较大,对分析结果影响较小,故这里选择的匹配时间差阈值为3 min,在不影响对比结果的情况下可以获得更多的对比样本。
2 测风数据对比
2.1 未剔除与剔除较大偏差测风对比
当两者风向方位角区间越过0°时,会出现风向差值绝对值大于180°的情况,会严重影响统计结果(例如风向分别为359°和1°的差值为358°,与实际2°的差值差距较大),故在匹配时作剔除处理[12],其剔除率为3.2%。通过上述方法匹配的测风数据对还存在一些较大偏差的离群值,Weber,et al[14]、吴蕾等[15]、王栋成等[16]在测风对比中将误差阈值确定为“三倍标准差”,将大于三倍标准差的测风数据作剔除处理。由于获取的L波段雷达测风资料是未经过气象资料业务系统质控的原始探空数据,其测风数据会由于雷达旁瓣跟踪、探空仪回答信号弱、频率失谐、电磁干扰和雷达故障等多种原因引起测风斜距不能正常跟踪[17],导致部分测风数据会出现较大偏差和疑误数据;并且获取的多普勒雷达测风数据是通过PUP软件回放雷达原始基数据得到的垂直风廓线产品,其中包含非线性风场、速度模糊数据、基数据含有超折射回波和噪声干扰等数据,会导致垂直风廓线产品出现较大误差,这些较大偏差和疑误数据不能反映多普勒雷达和L波段雷达测风的系统误差,故在匹配两者风向、风速时,将差值大于三倍标准差的测风数据作剔除处理,下文中没有标注未剔除的图表默认为剔除的测风对比。经过剔除后分别获得有效风向、风速对比数据为15 513对,其剔除率为3.58%。经计算剔除部分的测风数据,其风向标准差为97.07°,风速标准差为10.59 m·s-1,多普勒雷达风速平均值为6.36 m·s-1,L波段雷达风速平均值为10.55 m·s-1。
将未剔除和剔除大于三倍标准差的测风数据分别绘制散点密度如图1所示,剔除后风向、风速相关系数分别从0.95和0.90提高到0.97和0.94;风向、风速平均差分别由15.78°和2.23 m·s-1降低到13.15°和2.03 m·s-1,风向和风速标准差分别从27.05°和3.34 m·s-1降低到19.5°和2.65 m·s-1;平均差和标准差明显降低是由于剔除了较大误差的测风数据,剔除后得到的差值主要是由于两者测风原理不同和测量误差造成的。

图1 (a、b)未剔除三倍标准差和(c、d)剔除三倍标准差风向和风速散点密度:(a、c)风向(单位: °);(b、d)风速(单位: m·s-1)
2.2 按高度变化测风对比
由图2a可以看出,两者风向标准差在7 km以下随高度增加呈降低趋势,在7 km左右标准差最小,8 km以上有小幅度增加趋势。主要原因是由于大气高层比近地层较为稳定均匀,随着高度升高和风速增大,L波段雷达测风精度也会降低[18](表2),并且随着探空气球的水平漂移距离增大(华东地区探空气球上升高度达到12 km左右时水平漂移距离在冬季会超过30 km)[19],导致两者测风采样时空差异增大,故在8 km以上风向标准差增大。如图2b所示,风速标准差随着高度的增高呈增大趋势,主要是由于随着高度的增高风速值增大,L波段雷达的测风误差增大,并且随着探空气球水平漂移距离增大,两者测风采样时空差异也增大,导致其标准差增大;风速标准差在10 km以下均值为2.58 m·s-1,10 km以上均值为3.41 m·s-1。
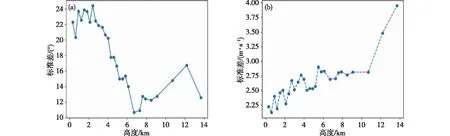
图2 (a)风向和(b)风速标准差随高度变化(风向单位: °; 风速单位: m·s-1)

表2 L波段雷达测风精度
如图3a所示,风速差值随高度增加呈递增趋势,总体风速差值平均为2.21 m·s-1。风速相对偏差在8 km以下呈递减趋势,8 km以上呈递增趋势,在8 km左右差值最低,总体风速相对偏差平均为24.48%。由图3b可知,风向具有较好的相关性,风向相关系数均较高且随高度变化幅度较小,其均值为0.97。风速相关系数随高度增加基本呈增大趋势,相关系数除近地面偏低以外,其他高度相关系数均较高,均值为0.94。主要原因是近地面受中小尺度扰动或下垫面影响较大,多普勒雷达VAD算法计算的平均风与实际风存在较大误差[20-21],导致近地面风速相关系数偏低。

图3 (a)风速差值和相对偏差与(b)风向、风速相关系数随高度变化
2.3 测风对比差值分布
风向和风速差值直方分布(图4)表明,多普勒雷达与L波段雷达的风向、风速差值分布基本呈正态分布,风向和风速差值分布与正态分布的拟合度分别达到97%和94%。多普勒雷达与L波段雷达风向风速总体差值平均分别为-0.48°和-0.72 m·s-1,总体上多普勒雷达风速小于L波段雷达,其中风向差值91%集中在-30°~30°,风速差值90%集中在-4~4 m·s-1。

图4 (a)风向和(b)风速差值分布直方分布
2.4 按风速分组测风对比
将测风按风速大小分成4组分别计算两者相关系数、平均差和标准差,如表3所示。风向相关系数在风速大于30 m·s-1时偏低,其他速度区间均较高;风向平均差和标准差随风速增大显著减小。风速相关系数随着风速增加相关系数呈增大趋势;风速平均差随速度增加也呈增大趋势,风速标准差在小于10 m·s-1时最低,其他速度区间均偏高。

表3 按风速分组多普勒雷达与L波段雷达测风对比
2.5 按降水与非降水分组测风对比
依据阜阳国家基本气象站2012—2017年每日累积小时降水量(基本气象站与多普勒雷达站直线距离500 m),将匹配的测风数据分为降水和非降水时段分别进行对比。由表4可知,风向、风速相关系数在非降水期间略有降低;风向在降水期间的平均差和标准差比非降水期间分别偏低21.7%和19.3%;风速在降水期间的平均差和标准差比非降水期间的分别偏低16.3%和16.4%。

表4 按降水与非降水分组测风对比
2.6 按季节分组测风对比
将剔除和未剔除大于三倍标准差的测风数据季节分布如图5所示,可见,风向和风速的四季相关系数均较高,其变化趋势不明显,剔除较大偏差数据后风向和风速相关系数略有增加。风向标准差在春、冬季较低,在夏、秋季较高,在剔除大于三倍标准差数据后总体风向标准差平均减少7.55°;风速标准差在夏季最低,剔除大于三倍标准差数据后总体风速标准差平均减少0.59 m·s-1。

图5 按季节分组测风对比:(a)风向相关系数;(b)风速相关系数;(c)风向标准差(单位: °);(d)风速标准差(单位: m·s-1)
3 结论
(1)为了更真实的反应多普勒雷达与L波段雷达的系统偏差,不受疑误和较大偏差数据的影响,将差值大于三倍标准差的测风数据剔除后,得到多普勒雷达与L波段雷达风向、风速相关系数分别为0.97和0.94,平均差分别为13.15°和2.03 m·s-1,标准差分别为19.5°和2.65 m·s-1。其中相关系数优于杨梅等[10](风向风速相关系数分别为0.74和0.75)、裴丽丝等[12](风向风速相关系数分别为0.787和0.788)和薛双青等[13](风速相关系数0.61)的计算结果。
(2)风向标准差在7 km以下呈递减趋势,8 km以上有小幅增加趋势。风速标准差随高度增高呈增大趋势,风速差值随高度增加呈递增趋势,总体风速差值平均为2.21 m·s-1。风速相对偏差在8 km以呈递减趋势,8 km以上呈递增趋势,在8 km左右达到最低,总体风速平均相对偏差为24.48%,低于薛双青等[13]计算的15个站点总体风速平均相对偏差51.6%和阜阳单站相对偏差36.2%;其中风速差值随高度变化趋势与裴丽丝等[12]计算结果基本一致。
(3)多普勒雷达与L波段雷达的风向与风速总体差值平均分别为-0.48°和-0.72 m·s-1总体上多普勒雷达风速小于L波段雷达,与薛双青等[13]分析结果一致。
(4)风向平均差和标准差随风速增大显著减小;风速平均差随速度增加呈增大趋势,风速标准差在小于10 m·s-1时最低为2.36 m·s-1,其他速度区间均偏高。
(5)多普勒雷达VAD风廓线数据在降水期间的测风偏差小于非降水。风向在降水期间的平均差和标准差比非降水分别偏低21.7%和19.3%;风速在降水期间的平均差和标准差比非降水期间的分别偏低16.3%和16.4%。

