两种面向数值同化的风廓线雷达资料质量控制方法比较分析
汪学渊 林银杰 刘德强 林立峥
(1 厦门市气象局 海峡气象开放实验室,福建 厦门 361012;2 福建省灾害天气重点实验室,福州 350001;3 福建省大气探测技术保障中心,福州 350001;4 福建省南平市气象局,福建 南平 353000;5 福建省气象台,福州 350001)
引 言
风廓线雷达是利用大气湍流对电磁波的散射作用进行探测的遥感设备,可以提供探测高度范围内的大气水平风速、风向、垂直气流、大气折射率结构常数等气象要素的观测,具有较高的时空分辨率,弥补了常规探空观测时空密度不足的缺陷。目前,风廓线雷达数据在监测预警、预报和数值同化中应用较为广泛,且取得了丰硕的成果。美国和日本的业务应用表明:风廓线雷达资料的同化对于数值模式0~12 h,尤其是3~6 h的预报具有正效果[1-2];北京、广东等地都初步开展了一些同化应用的个例试验,结果表明:在同化了经过质量控制处理的风廓线资料后,区域模式的预报效果取得了显著的改善,其中完善的质量控制流程则是资料得到有效同化应用的关键[3-5]。
近年来,中国气象局气象探测中心建立了完善的风廓线雷达资料质量控制和评估业务,分为台站级和国家级质控体系,台站级主要对功率谱资料进行质控,国家级主要对径向数据质控,为风廓线雷达资料的同化应用奠定了基础。采用变分方法进行资料同化时,观测误差和模式背景误差都必须要满足高斯分布的假设[4]。因此,在同化应用之前,必须识别和消除观测数据中不可靠或包含不能满足数据同化要求的离群值,确保观测场与背景场的差值(观测增量)近似与高斯分布相一致。
大气中的各气象要素基本上都是一维观测向量,目前针对单一要素(如温度、湿度等)的质量控制普遍采用了双权重标准差(Biweight Standard Deviation, BSD)方法,它通过给定的阈值来剔除离群值,质控效果较好[6-8]。然而,对于水平风场(u/v)而言,BSD方法无法实现对二维观测向量的同时质控。迭代加权最小协方差行列式(the Iterated Reweighted Minimum Covariance Determinant,IRMCD)[9]是在最小协方差行列式(MCD)[10-11]基础上发展起来的方法。MCD是应用稳健统计中最早的仿射同变和高鲁棒性多元离群点检测规则之一。自从引入计算效率较快的fast-MCD算法以来[12],MCD已被应用于医学,金融,图像分析和化学等领域。然而,由于传统MCD方法在检测离群值时存在一定量的误判,Cerioli[9]在其基础上引入了防“假阳性”机制以减少误判,应用于多元变量离群点检测。IRMCD可以对多维向量同时进行处理,ZHANG, et al[13]将IRMCD方法用于风廓线雷达水平风离群值检测发现:IRMCD对于二维风廓线雷达水平风观测资料的质控效果要好于BSD方法。研究从实际应用角度加深了对这两种质控方法的认识。然而,由于IRMCD依赖于形状分布参数,这些参数随数据集的大小而变化,ZHANG, et al[13]没有就这些参数对于质控效果的影响进行深入讨论。此外也没有给出晴雨条件下两种方法质控效果的对比研究。
为了进一步全面深入考察两种方法的差异性,本文将从统计指标、波形指标、概率密度分布、离群值分布多方面对IRMCD和BSD方法处理风廓线雷达资料离群值的能力和效果进行更深入的对比分析,揭示两种方法的差异性和优异性。
1 资料和方法
1.1 资料
风廓线资料挑选了福建省运行比较可靠的9部CFL-06型号的雷达资料,分别是:建瓯(58737)、建宁(58822)、罗源(58845)、连城(58912)、武平(58917)、德化(58935)、秀屿(58938)、平和(59125)和翔安(59140)。由于本文的重点在于考察IRMCD方法与BSD方法在混合雷达站点资料处理离群值过程中的性能和效果,所以将生成的风场小时数据作为原始观测数据。前期关于台站级和国家级质量控制有关部门和学者已做了大量研究,并取得了积极的研究成果,不再赘述。
利用9部风廓线雷达2018年2月2—11日10 d的小时风场数据作为原始观测数据,将观测数据分为降水和非降水天气,在这里降水和非降水的判定准则按照风廓线雷达垂直速度w≥2 m·s-1判定为降水,获得了65 000个非降水观测数据并在其中随机抽取5 000、10 000、30 000、60 000个观测数据;同时也获得了12 750个降水观测数据并在其中抽取5 000、12 750个观测数据,以考察IRMCD方法和BSD方法处理不同天气情况下不同观测样本量在统计指标和波形指标上是否有较大差异。
模式背景场数据选取了欧洲数值预报中心(ECWMF)哥白尼CS35数据库中高空u/v分量的小时再分析数据,并对模式背景数据在垂直和水平方向进行了插值处理,以获得与观测数据相同高度的背景场u/v分量,因此,u/v分量观测增量可以定义为:
ombu(i)=obsu(i)-mu(i),
(1)
ombv(i)=obsv(i)-mv(i),
(2)
其中:i=1,2,....n,n表示风观测数据总量;u,v分别表示风在水平方向两个分量。ombu(i)表示u分量的观测增量;ombv(i)表示v分量的观测增量;obsu(i)表示u分量的观测值,由OOBS产品文件中的风速V和风向θ根据-V×sinθ计算公式获得;obsv(i)表示v分量的观测值,由OOBS产品文件中的风速V和风向θ根据-V×cosθ计算公式获得;mu(i)表示u分量的模式背景值,mv(i)表示v分量的模式背景值。以下所有指标和参数的计算都是基于u/v分量的观测增量进行运算,如果观测增量判定为离群值,那么对应的原始观测数据定义为离群值。
1.2 迭代权重的最小协方差矩阵方法(IRMCD)
假设n个样本p个维度的数据集可以表示为:
Y=[y(1)......y(n)]T,
(3)
那么y(i)=(yi1......yip)T为第i个样本点,矩阵Y的平均值μ和协方差矩阵∑,如果Y中存在离群值,那么μ和∑已经被离群值污染。本文应用稳健统计分析方法,通过检测每个观测值鲁棒距离的平方与χp,1-α分布相差较大的距离定义为Y中的离群值,可以得到μ和∑的稳健估计值。其中1-α为χ分布的分位数,α一般取0.025。IRMCD是一种基于重加权MCD估计值而发展起来的稳健估计方法[14-15]。对于有限样本离群值检测的IRMCD方法的步骤如下:
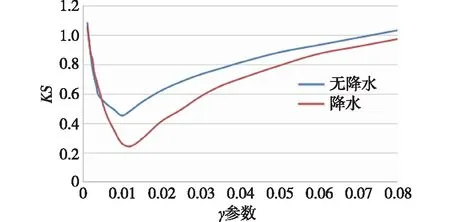
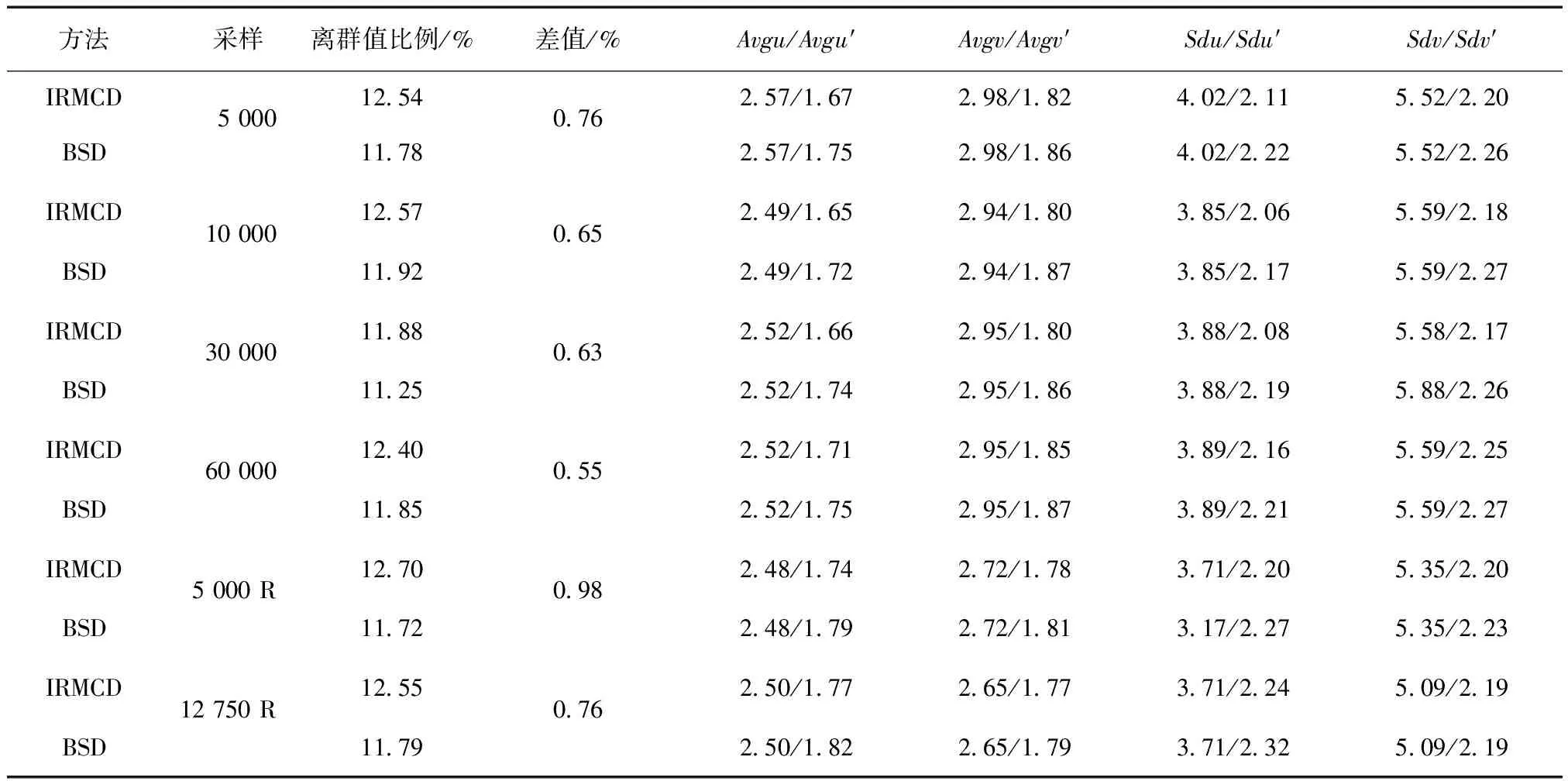
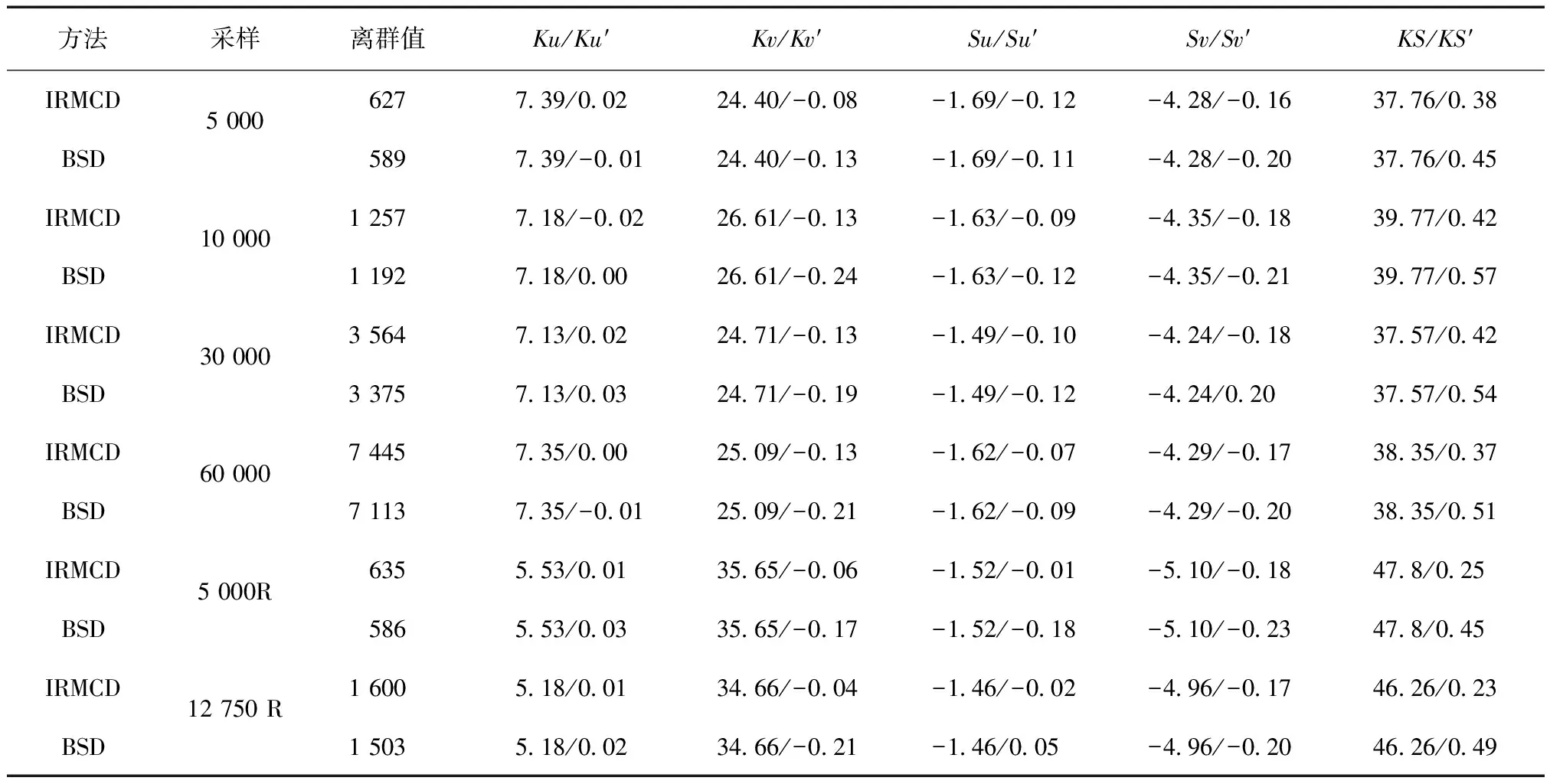
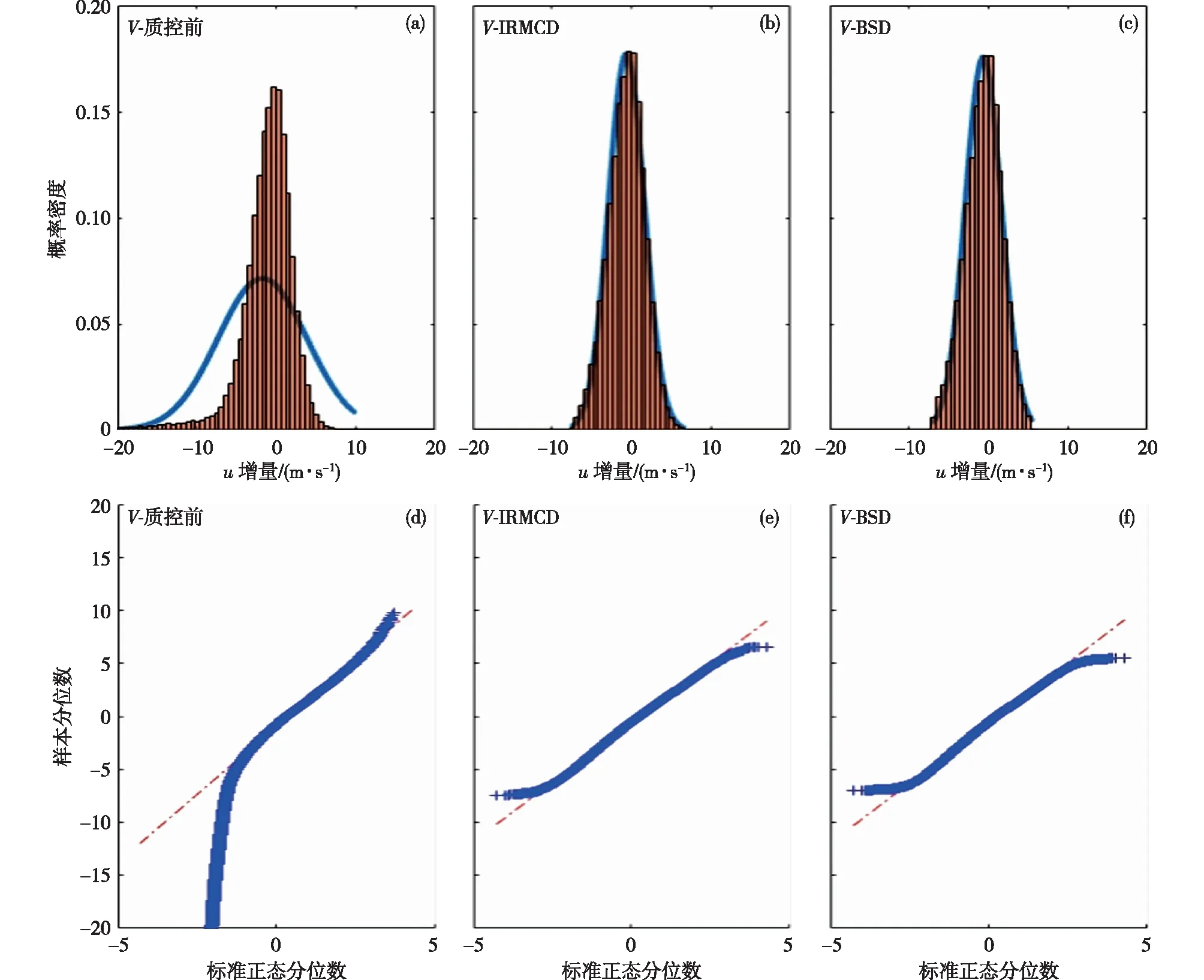
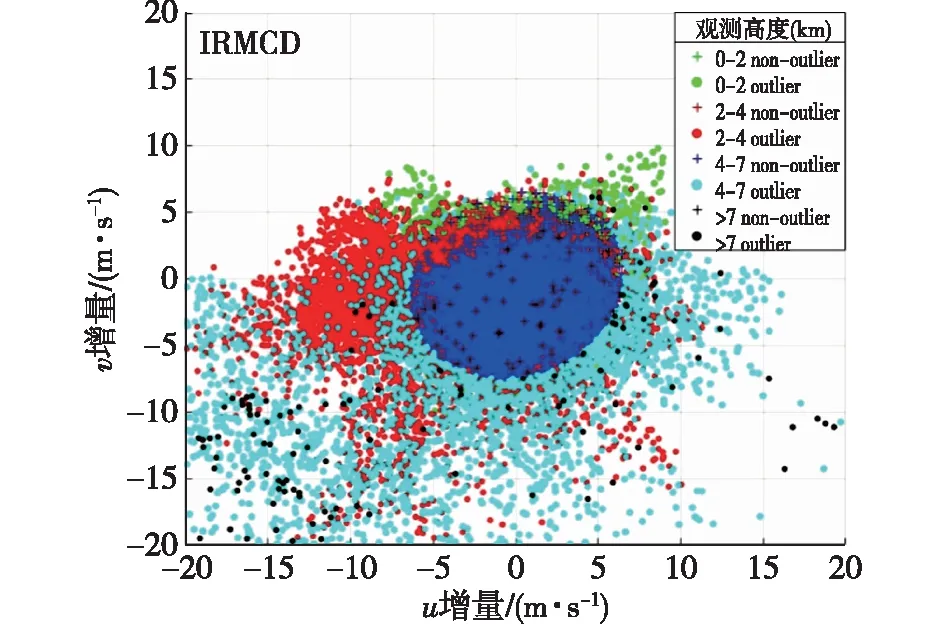
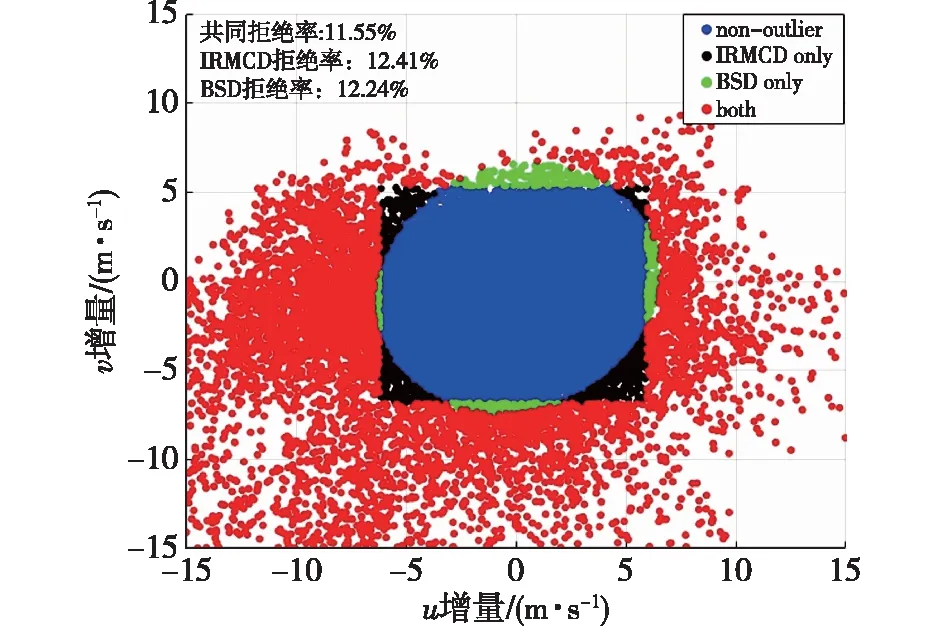
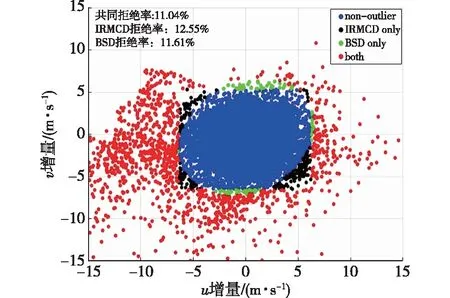
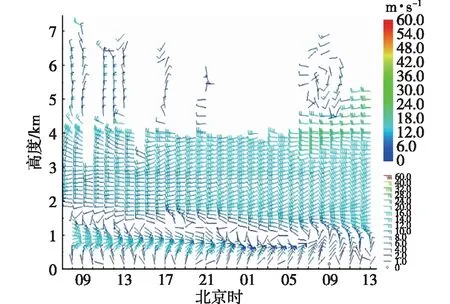
(1)在样本Y中,如果h(n/2≤h (4) 协方差估计为: ,(5) 其中:C0为比例常数[9]。 (2)在Y中,y(i)的鲁棒距离的平方可以定义为: ,(6) 它测量了观测值到假定非离群值的中心位置的距离。样本Y中所有观测值的权重系数可以通过DIS的值确定: (7) (3)为了增强效率,对y(i)进行加权步骤: (8) [y(i)-μRMCD]T, (9) 那么重新加权后鲁棒距离的平方为: (10) (4)参考文献[9]中, (12) 那么数据集Y中没有离群值。 按照上述步骤,使用预设的γ值,可以检测多变量数据集Y中的离群值。 双权重离群值判别计算方法(简称双权重标准法,又称 Z-Score 法)如下:设有n个样本(xi,i=1,2,...n) (1)计算每个样本量xi(i=1,2,..,n)的权重函数: (13) 其中:C为“敏感参数”,取C=7.5,当|wi|>1.0时,设定wi为1,M为样本量的中位数,MAD为绝对偏差中位数,即|xi-M|的中位数。 (14) 计算双权重标准差(BSD): (15) 对每一个xi计算Z-Score值: (16) 如果Zi>Zthresh,那么xi被认定为离群值[16],Zthresh为设定好的阈值,一般取2~4。 这里引入了峰度和偏度两个统计指标来形容观测增量数据的波形是否符合正态分布情况,峰度(Kurtosis)是描述总体中所有取值分布形态陡缓程度的统计量,峰度为0表示该总体数据分布与正态分布的陡缓程度相同;偏度(Skewness)是统计数据分布偏斜方向和程度的度量,当偏度接近0则可认为分布对称。两个指标都是以接近0值为最优值,因此可以组合峰偏值KS指标,表示如下: KS=|Ku|+|Kv|+|Su|+|Sv|, (17) 其中:Ku,Kv表示u,v分量的峰度;Su,Sv表示u,v分量的偏度。 那么当IRMCD和BSD方法分别取不同的参数γ和Zthresh时,质控后的观测增量的KS值应该具有最小值,KS取最小值所对应的参数γ和Zthresh值就是两种方法的最优解,就是本文所需要的最优观测增量数据。在以往的研究中,γ参数的典型取值为0.025[17-18],表示在样本集中期望2.5%比例的离群值,本文设定γ范围为0.080~0.001[13],每0.001的间隔考察KS值是否达到最小值,KS最小值所对应的γ值就是IRMCD处理此次观测样本增量的最优解;以同样的方式对Zthresh的取值范围设定在4.0~1.0,每0.01的间隔考察KS值是否达到最小值,KS最小值所对应的Zthresh值就是BSD处理此次观测样本增量的最优解。从总样本中随机抽取了无降水样本60 000个和降水样本12 000个,分别绘制了KS值随γ参数和Z阈值变化曲线(图1、2),无降水样本用蓝色表示,降水用红色表示,γ参数以0.001的间隔在0.080~0.001取值对应一个KS值,从图1中可以看出,KS值的变化曲线呈现不规则抛物线形状,有且仅有一个最低点,所对应γ参数就是IRMCD方法所需的最优解,当然对于不同的数据集KS最小值以及γ参数都会有所不同;同样,Zthresh以0.1的间隔在4.0~1.0取值对应一个KS值,从图2中可以看出,KS值的变化曲线同样呈现不规则抛物线形状,总能找到KS最小值,所对应Zthresh就是BSD方法所需的最优解。这说明所制定的通过峰偏值KS指标判定数据达到最优正态分布的合理性。 图1 KS值随γ参数变化曲线 图2 KS值随Z阈值变化曲线 从样本数据中随机抽取5 000、10 000、30 000、60 000个非降水观测数据和5 000和12 750个降水观测数据,分别利用IRMCD和BSD两种方法通过调整γ和Zthresh使KS值达到最小值,各个参数值如表1所示,其中Ku表示原始观测u分量增量数据峰度指标,Ku′表示经过IRMCD或BSD方法质控后的u分量增量数据峰度指标,以此类推。从峰度和偏度指标来看,在非降水样本中u分量的峰度Ku值保持在7.2左右,经过质控后Ku′下降到0.01左右,v分量的峰度Kv值保持在25左右,经过质控后Kv′下降到0.15左右;u分量的偏度Su值保持在-1.6左右,经过质控后Su′下降到0.1左右,v分量的偏度Sv值保持在-4.3左右,经过质控后Sv′下降到0.2左右。从波形指标上看,两种方法都起到很好的质控效果,在降水天气下峰度和偏度指标有着类似的趋势。但是从KS指标和离群值的数量来看,IRMCD始终比BSD方法的质控效果更好。图3展示了KS指标在不同样本下的变化曲线,IRMCD方法始终在0.4左右,而BSD方法始终在0.5左右,两者之间相差0.1,说明IRMCD方法质控后的数据更符合高斯或正态分布;从离群值的数量上来看,IRMCD方法始终比BSD方法判断的离群值要多,由表2可见,两种方法能够判别离群值占总样本的比例在11%~13%之间,但前者比后者要多0.6%,Avgu和Sdu分别代表u分量的绝对平均值和标准差,以此类推,经过两种方法的处理后,相对于原始数据都有极大的改进,质控后的Sdu基本保持在2.1~2.3,总体上IRMCD在绝对平均值和标准差指标都优于BSD方法。说明IRMCD方法无论在波形指标、统计指标和离群值数量上都优异于BSD方法,而且两种方法在样本的数量多少以及是否降水天气都不影响各自离群值判断能力。 表2 IRMCD和BSD不同采样统计指标表 图3 两种方法的KS指标对比曲线 一般来说,IRMCD和BSD方法在判定离群值的本质上是等价的:给定一个稳健的均值和标准差,数据集向量Y中的离群值通过它们与稳健拟合存在较大距离来识别。以非降水天气下60 000样本为例,图4、5分别为u/v分量的观测增量在不同方法处理后的概率密度和分位数—分位数(Q-Q)图,其中U-质控前表示u分量原始观测增量;U-IRMCD表示u分量观测增量经过IRMCD质控后的观测增量;U-BSD表示u分量观测增量经过BSD质控后的观测增量,以此类推。这能反映观测增量数据的分布情况,U-质控前和V-质控前的概率密度分布类似于高斯分布,但不是严格的高斯分布,可以看出陡峭的峰值和左右两侧分布的不对称存在异常值。更准确地说,在相对应Q-Q散射的两端存在较大差异,与其相对应的u/v观测增量的峰度值分别为7.35/25.09以及偏度值分别为-1.62/-4.29都说明原始观测增量数据分布严重偏离正态分布。从U-IRMCD和V-IRMCD的概率密度分布和Q-Q散点可以看出质控后的概率密度分布更接近于标准正态分布,Q-Q散点几乎以直线收敛,表明几乎所有离群点已被剔除,从相对应u/v观测增量的峰度值分别为0.0/-0.13以及偏度值分别为-0.07/-0.17,从数值上也说明质控后的数据逼近标准正态分布。同样的U-BSD和V-BSD的概率密度分布和Q-Q散点以及相对应的峰度值分别为-0.01/-0.21以及偏度值分别为-0.09/-0.20能得到相同的结论,说明两种方法在剔除离群值后都具有较好的正态分布,但是从峰度值、偏度值、峰偏值和标准差的指标对比来看,明显IRMCD方法的指标优于BSD方法,从概率密度直方图的底部两侧还是能看出IRMCD比BSD来得更加平缓;Q-Q散点两侧IRMCD比BSD更加靠近中线位置。值得注意的是,表1的两种方法的v分量偏度值始终保持在0.2左右,仍然需要最后的偏倚校正[13]。 表1 IRMCD和BSD不同采样数量波形指标表 图4 u增量概率密度直方图和相对应的Q-Q分布 图5 v增量概率密度直方和相对应的Q-Q分布 图6、7为u/v分量离群和非离群值散点分布,将进一步理清两种方法的差异之处。其中“+”表示非离群值,“.”表示离群值,并以不同的颜色代表观测值所在的高度,为了更加清晰地表示离群值和非离群值,在4~7 km的非离群值用蓝色表示,4~7 km的离群值青蓝色表示,可以看出0~2 km的离群值以绿色实心圆分布,表明v分量的观测值大于模式值,4~7 km的离群值以青蓝色实心圆分布,表明v分量的观测值小于模式值为主,在所有的离群值中4~7 km占据了一半以上,这是因为2月的温度与湿度低造成风廓线雷达的有效探测高度在6 km以下,在有效探测高度以上信噪比越来越弱,生成的风场可靠性降低,造成大量的离群值,同时也可以看到7 km以上存在很少的离群值,因为2月探测高度很少能达到7 km以上。从整体上来看,很明显,IRMCD和BSD两者最大的不同在非离群值聚集的形状上,BSD的非离群值更趋向于“方形”,而IRMCD的非离群值更趋向于“椭圆形”,这是由各自的算法所决定,BSD方法只能处理单向量,根据观测点偏离标准差的倍数来决定是否为离群值,而IRMCD方法能同时处理二维向量,通过二维向量距离最小协方差矩阵中心的距离是否满足特定分布来判定是否为离群值,这也是IRMCD方法的优势所在。 图6 u/v增量BSD离群和非离群值散点 图7 u/v增量IRMCD离群和非离群值散点 为了更进一步地理清两种方法在判定离群值的不同之处,将两种方法进行对比(图8),在非降水情况下两种方法都判定为离群值用红色表示,都判定为非离群值用蓝色表示,仅仅IRMCD方法为离群值但BSD方法为非离群值用绿色表示,仅仅BSD方法为离群值但IRMCD方法为非离群值用黑色表示,可以看出,红色点离群值所占比例为11.55%,IRMCD方法判定的离群值所占比例为12.41%,BSD方法判定的离群值所占比例为12.24%,因此大部分离群值两种方法都能识别,不同的是仅IRMCD方法的非离群值分布更趋向于0值轴附近,在图8中用绿色部分表示,仅BSD方法判定非离群值分布更趋向于“方形”对角线附近,在图8中用黑色部分表示,明显看出黑色点在4个角处且必然存在着离群值,但是BSD方法并没有识别出来,造成对非离群值的污染,而IRMCD方法识别的非离群值显得更加的平滑,虽然IRMCD方法也有存在错误识别离群值的可能性,但是相对于离群值来说小得多,几乎可以忽略不计。在降水情况下,如图9所示,展示了如上所述相近的分布,仅仅BSD识别出的离群值聚集在“方形”的对角线附近,而仅仅IRMCD识别的离群值聚集在0值轴附近。 图8 u/v增量无降水BSD和IRMCD散点 图9 u/v增量降水BSD和IRMCD散点 为了更好地展示原始观测风场和质控后数据的变化,图10、11分别用风羽图展示了雷达站点(58944)的风廓线,2018年2月8日08时(北京时,下同)至9日14时共计30 h的原始风场和IRMCD质控后的小时水平风廓线,对比发现,原始数据最大探测高度在7 200 m,质控后探测高度在5 000 m,图11风场廓线显示明显比图10干净、整洁、有规律,可见离群值主要分布在高空(4.5~7.5 km)和低空(0~0.5 km),原因是风廓线雷达在4.5 km以上接收到的回波信号很弱,几乎淹没在噪声信号中,造成功率谱信号识别错误,就会生成错误的水平风;同时由于风廓线雷达低空接收到的回波信号容易受地物杂波的干扰,这些在零频位置很强地物信号完全将大气湍流回波信号淹没,因此生成的水平风风速很小,方向杂乱没有规律。从图11中可以看出,IRMCD方法剔除离群值的能力优异,这里不再展示BSD方法处理后的廓线,因为处理后几乎与图11一样,在这么小的样本情况下几乎只有2~3个点的区别,这也能从前面表1的指标也能看出。 图10 2018年2月8—9日风廓线原始小时水平风廓线 图11 2018年2月8—9日IRMCD质控后小时水平风廓线 因此,这两种方法在3个方面有所不同: (1)在双权重标准差检查中,Y必须是单变量数据集。当应用于多变量观测(如风数据)时,需要分别对u/v分量进行异常值检查,当其中一个向量被认定为离群值,则该样本二维向量被处理为离群值;另一方面,IRMCD作为一种多变量离群点检测方法,可以直接应用于多变量数据集Y,即可以同时检测u/v分量的离群点,在用于风廓线雷达小时观测增量数据后,从波形指标、统计指标和离群值数量上都表明IRMCD更有效。 (2)它们的稳健均值和标准差是以不同的方式计算的,它们的识别规则也是如此。在IRMCD中,通过比较稳健距离的平方与具有形状参数分布的参考值进行比较,这些参数随着应用IRMCD的不同数据集而变化,获得的非离群值的分布近似“椭圆形”。在双权重检查中,设定距离双权重标准差的预定倍数作为识别离群值的阈值,获得的非离群值分布近似“方形”,这其中必然存在一定量的误判,也表明IRMCD比BSD方法有优势。 (3)IRMCD具有防止假阳性的机制。在IRMCD中,测试的第四步(公式12)是专门设计来防止在任何好的数据集中出现错误判定离群值情况[9],因为误报是传统MCD规则的明显缺点。在没有步骤4的情况下,IRMCD相当于正常的有限样本重加权MCD,直接执行第五步会导致错误地识别正确的数据集,因此,传统MCD和双权重标准差都存在着同样的缺陷。即使对于一个完美的数据集,离群值也或多或少被错误地检测到。这一点在ZHANG,et al[13]中已经有所验证,但是在本次样本执行同样的过程发现,利用两种方法都能识别出的非离群值进行试验发现两种方法都不能再识别出额外的离群值,因此,并不能完全通过这种方式来说明IRMCD方法比BSD方法更有效果,对于不同的数据集可能会呈现不同效果。 本文选取了2018年2月2—11日福建9部风廓线雷达的小时水平风观测数据与相应的模式数据之差,即观测增量,利用IRMCD和BSD两种方法分别进行质量控制,并对质量控制结果以不同的形式进行比较分析。主要总结如下: (1)制定了IRMCD和BSD质控方法获得最优解的判定指标峰偏值KS,同时通过KS指标的大小判断两种方法的优劣性,IRMCD的KS指标明显小于BSD方法的KS指标,说明IRMCD比BSD方法更接近正态分布。 (2)IRMCD方法可以同时应用在多维变量的离群值检测,而BSD方法只能应用在一维变量的离群值检测中,BSD应用在二维变量离群值检测的时候必须分别进行离群值检测,对于具有相关性的两个变量是不利的。从波形指标、统计指标和离群值数量上都说明IRMCD比BSD更有优越。 (3)IRMCD和BSD的稳健均值和标准差是以不同的方式计算的,它们的识别规则也是如此。在IRMCD中,通过比较稳健距离的平方与具有形状参数分布的参考值进行比较,这些参数随着应用IRMCD的不同数据集而变化,获得的非离群值的分布近似“椭圆形”。在双权重检查中,设定距离双权重标准差的预定倍数作为识别离群值的阈值,获得的非离群值分布近似“方形”,这其中必然存在一定量的误判,同时IRMCD具有防止假阳性的机制,这也减少了离群值的误判,也表明IRMCD比BSD方法有优势。 从多个方面都表明了IRMCD的在风廓线数据质量控制的优势,特别是对于二维向量离群值检测具有普遍意义,也可以应用在激光测风雷达、探空雷达、天气雷达等设备的风场离群值检测。也将为下一步在同化业务应用中提供了依据,同时今后也将该方法质控后同化应用于福建区域数值预报模式中,是否能改进数值预报效果,也是下一步的工作目标。




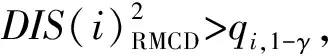
1.3 双权重标准差方法(BSD)

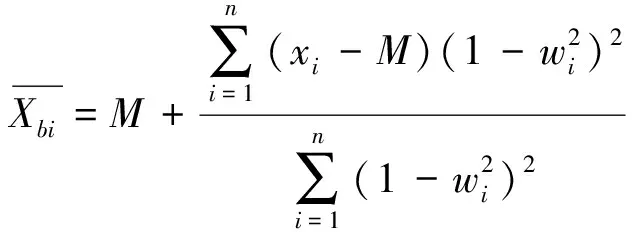
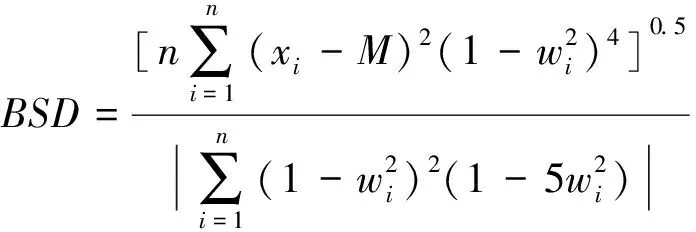
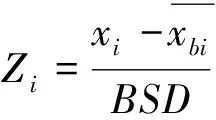
2 结果分析
2.1 基于正态波形指标的最优参数判定准则和指标分析


2.2 两种方法的概率密度和散点分布差异


2.3 IRMCD方法质控前后风场变化

3 结论

