棒-棒长空气间隙击穿电压的智能计算与分析

杨冰雪，姚修远，苏宇，丁玉剑*

(1.华北电力大学，北京 昌平 102206；2．中国电力科学研究院有限公司，北京 海淀100192)

特高压输变电工程的高压电气设备外绝缘介质大多由空气充当，长空气间隙的击穿特性是高压电气设备外绝缘设计的重要依据，而间隙结构和气象条件的改变都会对其造成较大的影响[1-3]。作为典型电极结构之一，棒-棒空气间隙击穿电压有效计算方法的提出对空气间隙放电特性研究具有重要意义。

数十年来，国内外学者开展了大量空气间隙放电真型试验，积累了一些实用的经验公式，但这些经验公式大多是基于统计回归的单参数模型，不能给出不同大气条件下空气间隙的击穿电压数值[4-8]。空气间隙的击穿电压与间隙结构、电压波形、大气条件等多种因素之间存在复杂的多维非线性关系，传统回归分析和统计方法难以对其进行有效的分析[9]。而神经网络、随机森林、支持向量机（SVM）等机器学习算法能够很好地处理这种多维非线性关系[10-11]，利用合适的机器学习算法建立不同气象条件下不同距离棒-棒长空气间隙击穿电压预测模型可以有效解决传统计算方法存在的不足。

早期研究者主要应用BP神经网络、自组织神经网络等人工神经网络算法构建空气间隙击穿电压预测模型，并在小范围测试集上取得了较好的预测效果[12-14]。然而，神经网络的参数较多，训练一个准确率高的神经网络往往需要较多的数据量和训练时间，其在小样本数据上的表现往往不如SVM[15]。支持向量机基于结构风险最小化原则训练模型，通过引入正则项可以有效避免过拟合现象，其在高维、非线性、小样本数据的分类和回归上表现良好[16]。近年来，基于SVM的空气间隙击穿电压预测方法越来越多地被提出[3,17-18]。由于空气间隙放电真型试验成本较高，研究者们往往只能得到少量放电数据，所以空气间隙放电数据是多维非线性的小样本数据，而SVM可以针对这样的数据建立精度较高的预测模型。目前空气间隙的智能计算模型大多都是针对较短间隙，而实际工程应用中长空气间隙才是常用的绝缘形式。对长空气间隙的击穿电压预测研究也大多只针对棒-板间隙，其他典型电极结构间隙则很少被涉及。

中国电力科学研究院在国家电网特高压直流试验基地的不同气象条件下得到了71组棒-棒长空气间隙操作冲击试验数据。本文选取棒-棒间隙距离、气压、干温和绝对湿度4个特征作为建模的输入变量，以棒-棒长空气间隙正极性操作冲击击穿电压作为输出，首先将数据归一化，以排除各变量数量级和量纲不同的影响，然后对4个变量进行灰色关联分析，计算出4个输入变量与击穿电压之间的灰关联度，定量分析其对棒-棒长间隙放电的影响。然后基于去量纲处理后的样本建立基于BOA-SVR的棒-棒长空气间隙正极性操作冲击击穿电压预测模型，在测试集上测试该模型的预测精度，验证这种计算方法的可行性。最后，利用该预测模型对特高压直流试验基地极端温湿度下的棒-棒间隙击穿电压进行了计算。

1 算法原理

1.1 灰色关联分析

灰色关联分析是一种通过系统各因素变化曲线几何形状的相似程度确定因素之间关联性的算法，以灰色关联度定量刻画不同因素间的关联性[19-20]。其基本步骤如下：

第一步，将原始数据进行归一化（或标准化等）。

第二步，确定参考序列：x0={x0(k)|k=1,2,…,n}；比较序列：xi={xi(k)|k=1,2,…,n}(i=1,2,…,m)。

第三步，计算参考序列与比较序列每个对应点的点关联系数：

第四步，计算参考序列与比较序列的灰色关联度γ(x0,xi)：

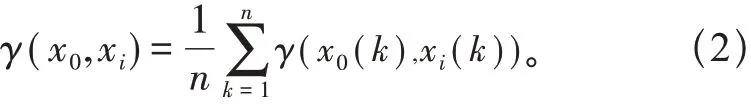
1.2 支持向量回归

SVR是一种监督式学习的方法，其主要思想是通过核函数将输入变量映射到高维空间，然后在这个高维特征空间中进行简单的多元线性回归[21]。

给定训练样本(x1,y1)，(x2,y2)，…，(xn,yn)，希望学得一个超平面使得f(x)与y尽可能接近：

式中：ω为回归系数，b为偏值项；给定一个小的正数λ，若有：

则可以认为f(xi)对yi的回归是无损的，即，支持向量回归允许有一定偏差，当偏差小于等于λ时可以忽略，反之则要计算损失。则SVR问题可形式化为

式中：C为正则化常数；lε为ε-不敏感损失函数：

引入非负松弛变量ζi、ζi和拉格朗日乘子

对ω、b、ζi和ζi'求偏导，令其等于0，将原问题转化为其对偶问题，然后引入核函数，将其原始数据映射到一个高维平面，求解后得到超平面表达式：

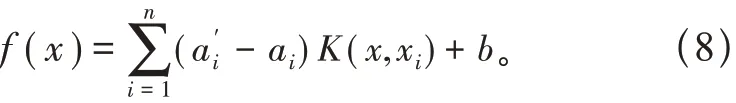
核函数的作用是避开高维空间中向量内积计算困难的问题，选择适当的核函数使构造一个高性能SVR模型的关键之一。常用的核函数有线性核、多项式核、径向基核函数（RBF）等，其中RBF是应用最广的一个。RBF是一种局部性强的核函数，在大样本和小样本数据上都有较好的性能，且参数较少，对噪声有较强的抗干扰能力。因此本文选取RBF作为SVR的核函数：

从上文的推导中不难发现有3个参数的值不能直接通过样本得到，需要人为选取，即：损失函数参数ε，正则化常数C和核函数参数γ。其中，ε影响着支持向量的数目，ε越小则支持向量越多，同时也能在训练样本上取得更高的回归精度，但会一定程度降低模型泛化能力。因此ε不能太小，一般取0.01较为合适，故本文选取ε=0.01，而C和γ的选取则通过参数寻优算法实现。正则化常数C反映了算法对超出软间隔的样本惩罚程度，若C过小会导致训练误差较大，过大则会导致泛化能力较差。而核函数参数γ反映了支持向量间的相关程度，γ过小会导致支持向量间相关度较低，泛化能力较差，而过大时会导致支持向量间的相关度较高，使得训练误差较大。因此C和γ都不宜取得过大或过小，本文设置其寻优范围为[0,50]。

1.3 贝叶斯优化

常见的参数寻优方法包括网格搜索、随机搜索和贝叶斯优化3大类。其中，网格搜索算法通过穷举的方式在一定范围内按照给定步长将待定超参数进行排列组合，然后计算比较不同组合训练的模型损失从而选取最优组[22]。这种方法的计算开销大，而SVR算法本身计算复杂度较高，使用网格搜索算法寻优效率较低。近年来，以一系列群智能优化算法为代表的随机搜索方法被广泛应用与机器学习模型的超参数选择中，然而，随机搜索算法往往容易陷入局部极小值，缺乏较强的全局搜索能力[23]。而贝叶斯优化（Bayesian optimization algorithm，BOA）是一种十分有效的全局优化算法，能够充分利用之前观测到的先验信息进行下一次优化，极大提高了搜索效率与全局搜索能力[24]。因此，本文将5折交叉验证的SVR均方误差作为优化目标，采用贝叶斯优化算法寻找最优的C和γ。

贝叶斯优化使用代理函数代替目标函数，在采集点的过程中不断拟合更新该代理函数，使之逐渐逼近真实目标函数，根据拟合结果主动选择最有潜力的评估点进行评估，避免不必要的采样[25]。其基本流程如下：

（1）选取一个数据点x使得采集函数最大；

（2）将x输入目标函数得到其对应的目标值y；

（3）使用新数据（x,y）更新代理函数；

（4）重复上述3个步骤直至达到迭代停止条件。

本文中，代理函数为TPE（tree parzer estimator），采集函数根据代理函数的后验概率分布构造而来[26]。

2.4 误差分析方法

本文采取以下两种指标分析模型在测试集上的误差。

绝对误差百分比（absolute percentage error，APE）

平均绝对误差百分比（mean absolute percentage error，MAPE）

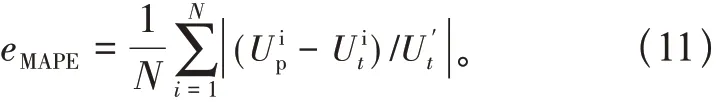
式中：Ut和Up分别为样本的试验值和预测值，N为预测样本个数。

1.5 方法流程图

基于贝叶斯优化支持向量回归算法，本文提出的棒-棒长空气间隙击穿电压预测方法流程图如图1所示。

图1 基于BOA-SVR算法的击穿电压预测流程

2 模型构建与分析

2.1 基于BOA-SVR的棒-棒长间隙击穿电压预测模型

本文以不同气象条件下的71组棒-棒长空气间隙操作冲击试验数据作为样本，选取棒-棒间隙距离d（m）、干温t（℃）、气压p（kPa）和绝对湿度h（g/m3）4个特征作为建模的输入变量，构建基于BOA-SVR的棒-棒长空气间隙正极性操作冲击击穿电压预测模型。基于试验数据的样本分布情况，选取涵盖2～7.24 m间隙距离的15组数据作为测试集，其余数据作为训练集。训练集和测试集的特征取值范围如表1、表2所示。

表1 训练数据输入特征范围

表2 测试数据输入特征范围

首先，对归一化后的全部样本进行灰色关联分析，取参数ζ=0.5，得到4个特征与击穿电压的灰关联度如图2所示。

由图2可知，上述4个灰关联值均大于0.55，表明4个因素均对棒-棒间隙放电有不可忽视的影响，选取它们作为击穿电压预测模型的输入变量是合理的。其对放电的影响力由高到低排序为：间隙距离、气压、温度、绝对湿度。其中间隙距离与击穿电压的灰关联度显著高于气象因素，而气象因素中气压的影响力高于温湿度。

图2 4个影响因素与棒-棒间隙击穿电压的关联度

将5折交叉验证的均方误差作为适应度函数，通过贝叶斯优化算法搜索SVR的最优参数。BOA的参数设置为：迭代次数=1000，代理函数为TPE，C和γ的寻参范围为[0,50]。输入训练集，得到最优参数：C=38.38，γ=0.09。寻优过程中，模型损失随两参数变化的情况如图3、图4所示。

图3 模型损失随惩罚系数变化情况

图4 模型损失随核函数系数变化情况

在得到的最优模型下，测试集的预测结果如表3所示。结果表明：测试样本的最大绝对误差百分比为8.5%，平均绝对百分比误差为3.2%。15个测试样本中，模型预测的绝对误差百分比在5.5%以下的有13个，表明该模型预测效果良好。将预测与试验结果绘制到同一张图上，并使用幂函数拟合试验数据得到相应曲线，如图5所示。由图5可知模型预测结果与试验值相近，且预测值更接近拟合的曲线，验证了本文所提出的棒-棒长空气间隙击穿电压智能计算模型的有效性。

图5 测试集试验值和预测值对比

表3 BOA-SVR模型预测结果

3.2 极端温湿度环境下棒-棒间隙的击穿电压计算

综合考虑北京市气象参数的变化范围和棒-棒间隙50%击穿电压预测模型中训练数据的气象参数变化范围，由于训练模型中缺少高温干燥条件的数据，所以本文选取了高温高湿、低温高湿、低温干燥3种极端气象条件下的气象参数如表4所示。对表4中的3种极端温湿度条件下的棒-棒间隙50%击穿电压进行计算，计算结果如图6所示。通过对3种极端温湿度条件下的棒-棒间隙50%击穿电压计算结果进行分析，发现：高温高湿条件下的棒-棒间隙50%击穿电压最小，而低温干燥和低温潮湿下的棒-棒间隙50%击穿电压差距不大，可能是因为这两种条件下的绝对湿度相差仅有1.8 g/m3，而模型代表湿度的输入是绝对湿度而不是相对湿度，因此导致这两种情况的预测值极为相似。另外，在间隙距离为2 m时，不同气象的击穿电压最高相差22.0%，而在10 m时，不同气象的击穿电压最高相差降为9.1%，表明随着间隙距离的增大，气象因素对放电的影响占比更小，这正与试验得到的结论相符。

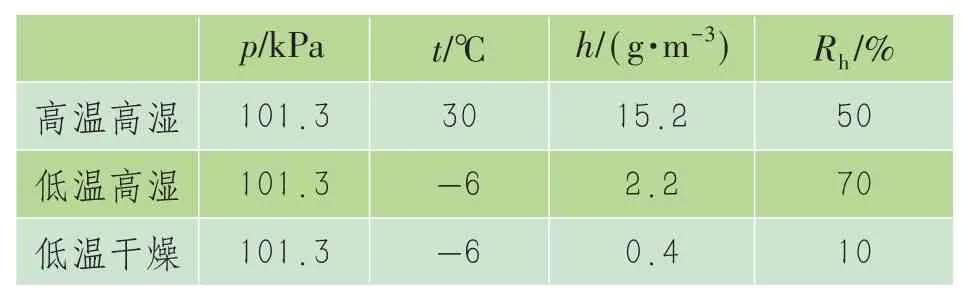
表4 不同极端环境的参数选择

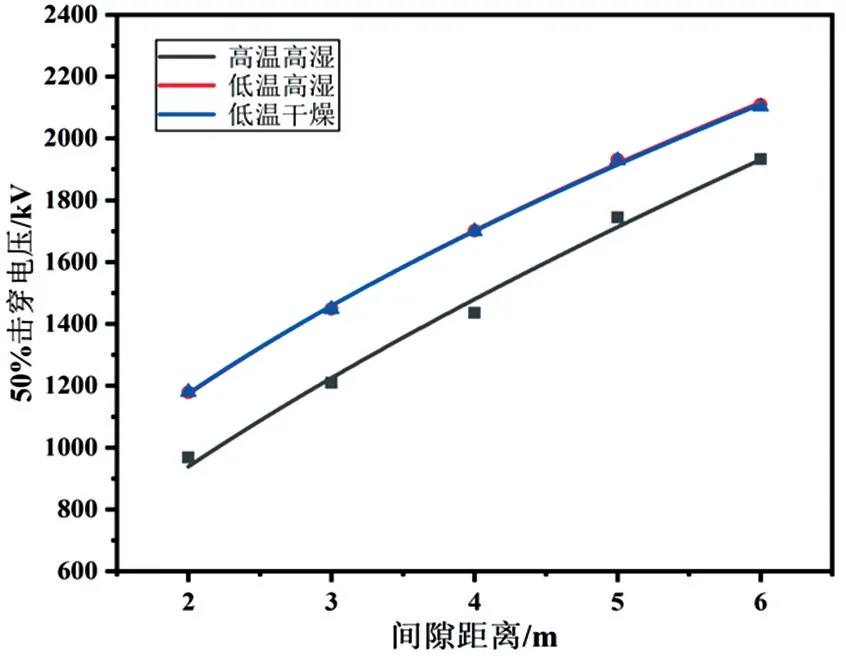
图6 极端环境下的棒-棒间隙放电特性曲线预测

4 结论

本文以棒-棒间隙距离、气压、干温、绝对湿度作为输入变量，构建了基于BOA-SVR算法的棒-棒长空气间隙50%击穿电压预测模型，得到如下结论。

棒-棒间隙50%击穿电压的影响因素与其的灰关联度排序从高到低依次为：间隙距离、气压、空气温度、湿度。

构建了基于BOA-SVR算法的棒-棒长空气间隙50%击穿电压预测模型，模型在测试集上的最大绝对误差百分比为8.5%，平均绝对百分比误差为3.2%。15个测试样本中，模型预测的绝对误差百分比在5.5%以下的有13个，验证了本文算法的有效性。

基于构建好的棒-棒长空气间隙50%击穿电压预测模型，对高温高湿、低温干燥、低温高湿3种极端温湿度条件下的棒-棒间隙50%击穿电压进行计算，结果与试验得到的规律基本一致。