2维地震波场的精确解及其无网格数值模拟

曹艳华,朱挺欣,王 军

(华东交通大学理学院,江西 南昌 330013)

0 引言

地震波传播理论是地震波场正演模拟的基础，而地震波场的正演模拟又是在地震科学中一项非常重要的技术手段，它被广泛应用于地震勘探和天然地震中，在采集、处理和解释地震数据的过程中起着不可或缺的作用[1-3].

地震波场的正演模拟主要有积分方程法[4]、波动方程法[5-6]、射线追踪法[7]等.波动方程法又可分为有限差分法、有限元法和谱方法等.本文首先通过升降法求出2维地震波场的精确解，再利用有限差分法和无网格方法对其进行数值模拟，进而对地震波场的运动状态、动力学特征进行详细分析.

传统的有限差分法是最早应用于微分方程的数值模拟方法，该方法的基本原理是利用差商近似代替在方程中的微商而得到的，该方法具有计算效率高、占用内存相对较小的优点，是在勘探地震学中应用最广泛的数值计算方法.汪勇等[8]在求解2维声波问题时基于频散关系分析思想，采用最小二乘法建立误差目标函数，再利用拉格朗日乘子法对目标函数进行求解，得到了优化后具有4～10阶精度的有限差分格式，将2阶导数的五对角紧致差分格式扩展到2n阶精度.Peng Chong等[9]针对颗粒流采用由泰勒展开和重整化方法得到的2阶一致空间格式提出一种新的拉格朗日差分动力学(LDD)方法.尽管传统的有限差分法在某些方面得到了改进，但是它只能对规则区域进行求解，非常依赖于网格的剖分，具有严重的数值频散性等缺点.

不同于传统的网格类方法，近年来发展起来的无网格方法是根据计算节点来近似而不需要网格连接的计算方法，该算法适用于各种规则和不规则区域的数值模拟，能够有效地解决网格类方法难以解决的问题.到目前为止，无网格方法已成功应用于Helmholtz方程[10]、微生物驱动数值模拟[11]、凹凸边界形状热弹性问题[12]、中心刚体-旋转柔性梁的动力学问题[13]等的研究中，这充分显示了无网格方法在求解相关问题时的优势.曹艳华等[14]提出的多项式特解法在求解微分方程时具有较高的数值精度，且算法极其稳定.Wu Shaowei等[15]针对带修正的Dirichlet-to-Neumann边界条件水下声辐射问题,提出一种改进的无单元Galerkin插值(IIEFG)方法.王珊珊等[16]利用Laplace方程的基本解和径向基函数(RBFs)提出一种求解多连通域的Poisson方程柯西问题的无网格数值方法.曹艳华等[17]将多项式特解法与Houbolt方法相结合，提出一种发展方程的混合方法，该方法在初始时刻采用高精度的时空多项式特解法对发展方程进行求解，获得的高精度数值解作为Houbolt方法的初值.田巧娴等[18]提出了数值求解3维热传导方程的一种无条件稳定的高精度半显式差分方法.M. Hussain等[19]对变系数的时间分数阶高阶扩散波方程(TFHODWEs)提出基于隐式时间步进算法的无网格谱插值方法，通过径向基函数(RBFs)和点插值方法(PIM)得到无网格形函数，对微分方程进行求解.李订芳等[20]提出了一种基于截断奇异值分解(TSVD)的正则化和径向基函数(RBF)的改进的无网格方法.

本文讨论如下2维地震波方程:

(1)

其中Δu=uxx+uyy.采用升降法推导出2维地震波场的精确解,采用无网格方法对2维地震波场进行了数值模拟，并对模拟的结果与传统的有限差分法进行比较.本文的无网格方法具体采用改进的时空多项式特解法，该算法将原来空间上的d维问题转换为时空域上的d+1维问题，并结合多尺度技术减少特解法生成矩阵的条件数,使得多项式基函数在多项式基阶变高时是稳定的.

1 2维地震波方程的精确解

本部分讨论初值问题(1)的精确解.下面给出一些定义及引理.

(2)

其中B(l,r)是以l为圆心、r为半径的圆,∂B(l,r)为圆周,U(l;r,t)为在圆周∂B(l,r)上函数u(·,t)的平均值.

定义2[19]类似地,令h(m)=h(x,y)=0,g(m)=g(x,y)=x2(x+y),定义

(3)

(4)

引理1[19](欧拉-泊松-达布方程) 令(x,y)∈R2,且u(x,y,t)满足方程(1).不妨设a=1,则U(l;r,t)满足

(5)

证令m=l+rz,有

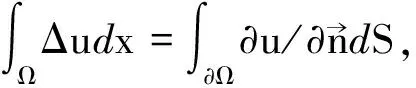
(6)

其中α(n)表示n维单位球的体积，这里n=2.因此,

所以

接下来求3维问题的解.同样,不妨令a=1.当n=3时,式(5)变为

Utt(l;r,t)-Urr(l;r,t)-2Ur(l;r,t)/r=0,(r,t)∈R+×(0,∞).

下面消去2Ur(l;r,t)/r.令

(7)

(8)

(9)

事实上,因为

(10)

由式(2)可知

其中l=(x,y,z).再由式(3)～(4)、(7)～(8)、(10)可得

于是,

(11)

式(11)表示的是3维空间变量l=(x,y,z)的解.下面采用降维方法求出2维空间变量l=(x,y)的精确解.所谓降维法是指若方程

的解与z无关,则u=u(x,y,z,t)满足2维波动方程.

事实上,当n=2时,假设u(x,y,t)是方程(1)的解,记

(12)

那么方程(1)变成

(13)

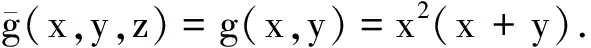
(14)

化简式(14)得到方程(1)的精确解为

u(x,y,t)=x2(x+y)+a2t2(3x+y).

(15)

取a=1,当t=0时,精确解为u(x,y)=x2(x+y)(见图1).当t=1时,精确解为u(x,y,1)=x2(x+y)+3x+y(见图2).

图1 当t=0时的精确解

图2 当t=1时的精确解

2 2维地震波方程的数值解

2.1 有限差分法

本节讨论方程

(16)

为了衡量数值算法的精度,定义如下误差:

xi=ih,yj=jh,0≤i,j≤m,

tk=kτ,0≤k≤n,

其中h=1/m为空间步长,τ=T/n为时间步长.定义在该矩形网格上的网格函数为

第2步:微分方程离散化.利用泰勒级数展开得到

(17)

(18)

(19)

代入方程(16),得到

(20)

因此,建立的差分格式为

(21)

其中r=τ/h为网格比,局部截断误差为O(τ2+h2).

2.1.2 数值结果 取空间步长h=0.1、时间步长τ=0.001并代入式(21)中，则当t=0.1时近似解在格点上的绝对误差如图3所示，均方根误差为0.009 3.当t=1.0时近似解在格点上的绝对误差如图4所示，均方根误差为0.671 9.在本算例中，网格比r=τ/h=0.01,因此3层的差分格式收敛，但计算精度整体不高，故简单的有限差分格式不适合解此类发展方程.

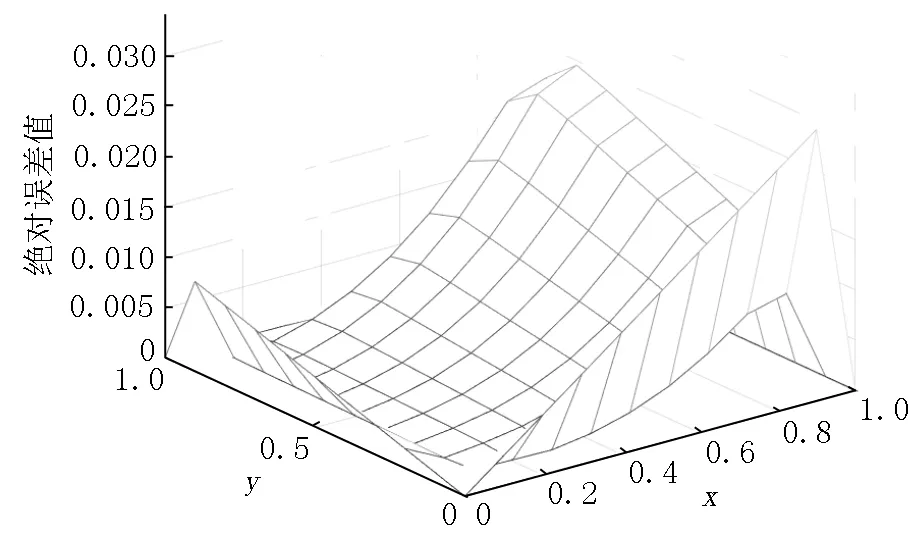
图3 当t=0.1时的近似解绝对值误差

图4 当t=1.0时的近似解绝对值误差

2.2 无网格方法

2.2.1 时空多项式特解法 本节简要介绍运用时空多项式特解法求解2维地震波动方程的初边值问题的一般步骤.

考虑如下的2维地震波方程:

(22)

其中函数f(x,y,t)、u0(x,y)、u1(x,y)和g(x,y,t)为给定函数.

假设方程(22)的解u(x,y,t)可以通过一组线性无关的特解多项式Φijk(x,y,t)的线性组合来近似

(23)

其中Φijk(x,y,t)为满足LΦijk(x,y,t)=xiyjtk的多项式,微分算子L=∂tt-(∂xx+∂yy)+I.

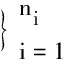
将求出的待定系数{aijk}代入式(23),得到方程(22)的近似解.引理2提供了求特解多项式Φijk(x,y,t)的方法.

引理2[21]对于一般的3维2阶常系数微分方程，令(w1,w2,w3)=(x,y,t)

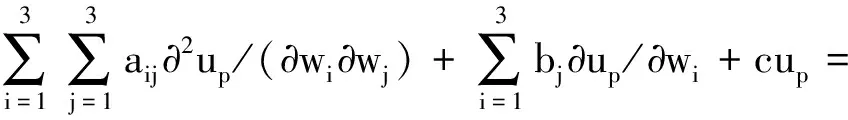
(24)

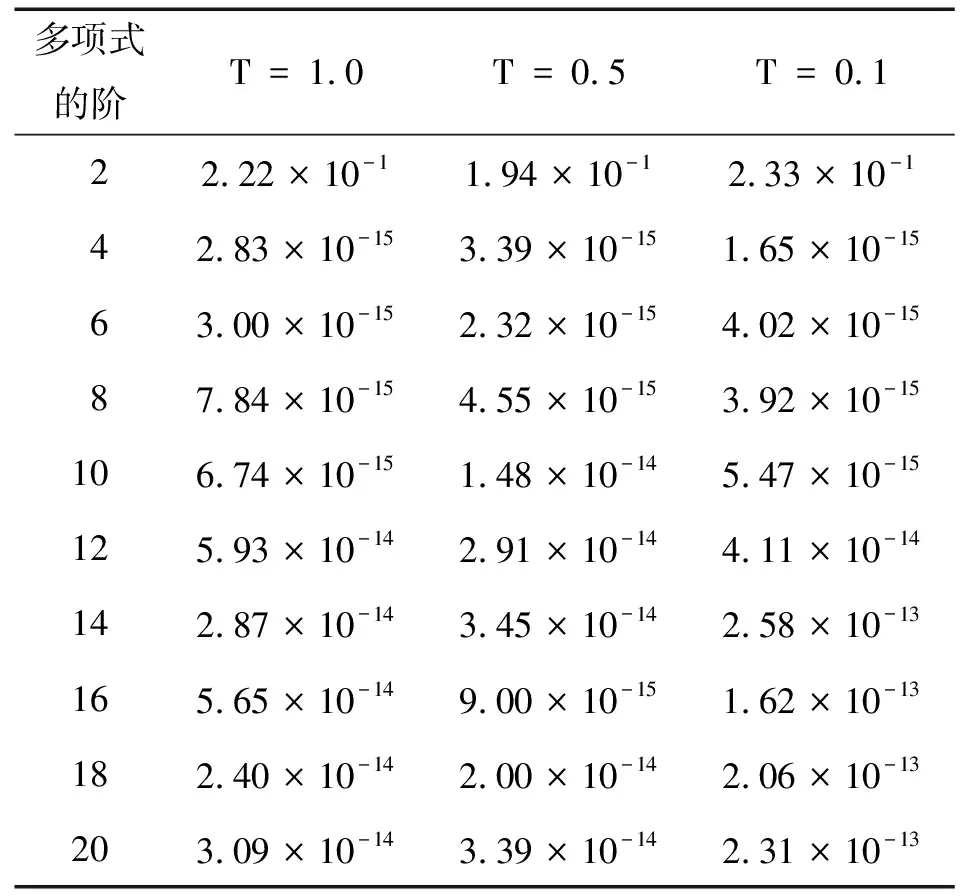
表1 时空多项式特解法求得的近似解的均方根误差

多项式特解的阶

3 结论

本文主要使用升降法研究2维地震波场的精确解及其数值模拟.当采用有限差分法求解此类方程时算法精度不高.当采用无网格类方法的时空多项式特解法时算法的精度很高，接近机器精度，而且算法的稳定性极好.但基于配点法的无网格类方法需要一定数目的配点，所得的系数矩阵为稠密矩阵，随着多项式特解阶的提高，系数矩阵的条件数增长较快.下一步的工作是研究局部多项式特解法，以期得到的系数矩阵为稀疏矩阵.