简述数形结合思想在初中数学教学中的渗透
文/李 敏
引 言
初中数学知识体系主要分为三大类:一是关于数字的知识,如实数、代数、方程及方程组、不等式及不等式组等;二是关于图形的知识,如平面几何、立体几何;三是数形结合的知识,主要体现在解析几何上。数形结合思想本质上是将直观的图像和抽象的数学语言相结合,在图形问题和代数问题之间相互转化,实现代数问题几何化,几何问题代数化[1]。随着教学理念的转变和教学方法的创新,近年来数形结合思想在初中数学教学中的应用越来越广泛,已经成为解决实际问题的一种重要方法。以下笔者结合实践经验,针对数形结合思想在初中数学教学中的应用和渗透进行探讨。
一、数形结合的使用原则和常用方法
(一)数形结合的使用原则
1.等价性原则
数形结合并不是在所有数学问题中均可以应用,而是当代数和几何具有等价性时,才能实现两者的转化。一些图形的表达方式有局限,提供的信息量少,盲目采用数形结合,会导致解题不严谨。以数轴为例,数轴上的点和实数是一一对应的关系,这两者具有等价性,因此可以采用数形结合思想。
2.双向性原则
对于一些数学问题,如果只进行代数分析或几何分析,都不能明确知识的内在联系,此时便可采用数形结合,实现图形和代数的双向转化。以平方差公式、完全平方公式的推导为例,基于双向性的数形结合思想,一方面是利用多项式的乘法法则,从数的角度进行推导;另一方面是利用四边形面积的变化,从形的角度进行推导[2]。如此便可将数字问题直观化、图形问题逻辑化,方便学生理解。
3.简单性原则
针对不同的数学问题,采用的解题方法也不同,而且解题方法可能不止一种。有些问题采用图形法更加简单快捷,有些问题则需要精准计算。在应用数形结合时,学生应找到最简单的解题方法,而不是机械性地将数与形结合,应对复杂问题进行简单化处理,以形成清晰的逻辑和解题步骤。
(二)数形结合的常用方法
1.以形助数
以形助数有利于学生直观理解抽象问题,帮助学生形成清晰的解题思路。初中生的阅历少,而且思维容易受到多方面因素的影响,理解抽象知识时有难度。以形助数,就是利用简单的图形来理解复杂的数学问题,形成一定的解题技巧。
2.以数解形
以数解形有利于分析图形结构特点,实现从几何到数量的有效转化。学生掌握几何中的数量关系后,结合图形的结构特征,将两者整合起来就能形成解题思路,为解答更复杂的数形结合问题打下基础。初中数学教材中有很多使用字母或数字表示的公式,在教学这些公式时,教师可以采用数形结合。教师在教学中渗透这一思想时,应注重培养学生的信息筛选能力,引导学生对数量关系进行深入理解,从而使其掌握相应的图形结构[3]。
3.数形互变
数形互变有利于把握数与形的关联,在解题中实现数形互助。教学时,教师应引导学生从已经掌握的数学知识和结论入手,探究数和形之间的变化,使其深入挖掘这两者的内在联系,更好地感知数字与图形。
二、数形结合思想在初中数学教学中的重要价值
(一)激发学生的学习兴趣
和小学数学相比,初中数学涉及的知识体系有所扩大,学习难度也有所提高。初中生的思维方式正处于过渡时期,他们对理论知识的学习兴趣不浓,学习效率低下。在教学过程中,教师采用数形结合思想可以改变这一现状,图形和数字的结合、转化、互变,能为学生创设一个真实的学习情境,有助于激发学生学习兴趣,提高学生学习积极性,使其自觉参与到课堂活动中。
(二)强化知识记忆能力
数学是一门工具性学科,要想学好数学、用好数学,学生首先要牢牢记忆概念、特征、定理、公式等基础知识,如此才能在解决问题时选用相应的知识点。学生在采用数形结合思想记忆数学知识时,能在脑海中形成具象的画面,不但记得准确,而且记得时间更长。如此,在面对真实的数学问题时,学生才能做到“下笔如有神”。
(三)培养学生的数学思维
数学知识源于生活,同时又为实际生活服务。从生活中提炼数学元素,有助于培养学生的数学思维,使其真正做到学以致用[4]。在学生采用数形结合思想解决抽象问题时,教师要引导学生观察、联想、分析,拓展学生思维空间。学生掌握数形结合思想,又能反作用于学习过程,将不同知识点融会贯通,建立属于自己的知识体系。
三、数形结合思想在初中数学教学中的应用
以下结合例题,介绍数形结合思想在实数、整式运算、坐标系、函数、方程中的应用情况。
(一)实数
例题1:如图1,数轴上有A、B、C、D四个点,根据它们各自的位置,判断哪一个点最接近
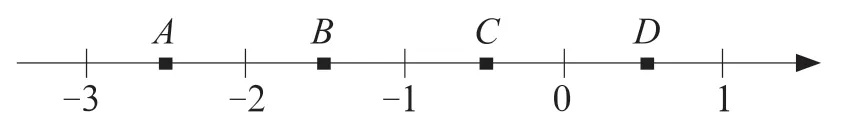
图1
数轴上的点和实数一一对应,利用数轴可以进行实数加减,也能表示相反数、绝对值、不等式的解集等。例题1 本质上是求解11-的大小,可按照以下步骤进行:先计算,再计算,最后计算11-。解题过程如下。
(二)整式运算
例题2:图2是由4 个全等的长方形拼成,根据中间空白部分面积的不同表示方法,写出一个关于a、b关系的恒等式。

图2
图形比较形象直观,但定量计算时要依靠代数。对于复杂的图形,学生应从不同角度观察图形的特征,从而发现隐藏条件,用数量正确表示图形。针对例题2,可以采用以数解形法,解题过程如下。
观察图形,中间空白部分的面积有两种表示方法:①先得出中间正方形的边长,然后根据面积公式计算面积,即中间正方形的边长是(a-b),面积表示为(a-b)2。②先计算大正方形的面积,然后减去周边4个长方形的面积,大正方形的边长是(a+b),面积表示为(a+b)2;1 个长方形的面积是ab,4 个长方形的面积之和是4ab;因此中间小正方形的面积是(a+b)2-4ab。即根据图2得到a、b关系的恒等式是:(a-b)2=(a+b)2-4ab,刚好是完全平方公式的推导过程。
(三)坐标系
例题3:如图3,已知正方形OABC的边OA在x轴正半轴上,边OC在y轴正半轴上,边AB上有一点D坐标是(4,3)。当△CBD绕着点C旋转90°,那么旋转后点D对应的点D’坐标是( )。
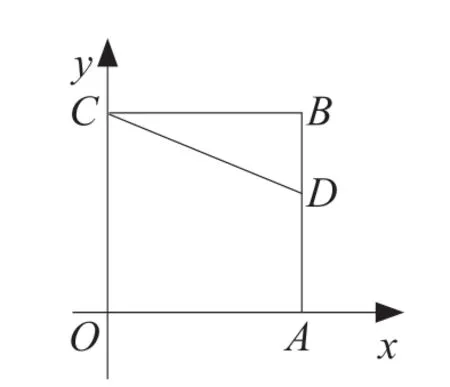
图3
A.(1,8) B.(-1,0)
C.(8,1)或(-1,0) D.(1,8)或(-1,0)
该题考查的是在平面直角坐标系中,坐标点位和图形变换的关系。围绕已知条件,解题时重点有两个:一是△CBD旋转90°分顺时针和逆时针两种情况;二是根据图形特征计算点D’的坐标。解题过程如下。
因为点D(4,3)在边AB上,可得BC=OA=4,AD=3,BD=1。①当△CBD顺时针旋转90°,点D’在x轴上,此时OD’=1,即D’坐标是(-1,0)。②当△CBD逆时针旋转90°,点D’到x轴、y轴的距离分别是8 和1,即D’坐标是(1,8)。综上,点D’的坐标是(-1,0)或(1,8),答案选择D。
(四)函数
例题4:已知一次函数y1=kx+b和y2=x+a的图像如图4,对于以下结论:①k<0;②a>0;③当x<3时,y1<y2,正确的数量是( )。
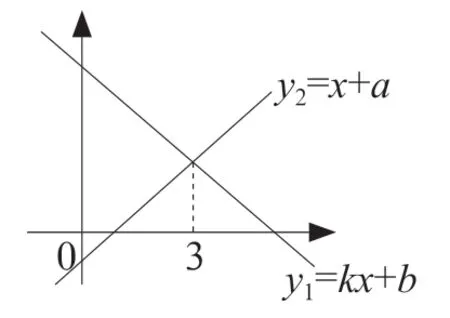
图4
A.0 B.1 C.2 D.3
数形结合思想在函数中的应用具有代表性,因为函数不仅有表达式,还有对应的图像[5]。表达式和图像的相互转化,能提供全面的信息,这些信息就是解题关键,解题过程如下。
分析图像可知:①y1=kx+b的图像呈下降趋势,和y轴相交于正半轴,说明k<0,b>0。②y2=x+a的图像呈上升趋势,和y轴相交于负半轴,说明a<0。③两个函数的交点横坐标是3,从图像位置关系看,x<3 时,y1的图像在y2上方,说明y1>y2。因此,正确结论只有1 个,答案选择B。
(五)方程
例题5:如图5,已知某花园是长方形ABCD,长度为50m、宽度为30m,规划在内部修建3 条宽度相同的道路,其中两条和边AB平行,另一条和边BC平行,其余部分种植花草,每一块草地的面积是50m2,问道路宽度是多少?

图5
方程及方程组是解决几何问题的有效方法,根据已知条件和图形特征列出方程然后进行计算,可以减少计算量,是数形结合思想的重要体现。本例题考查的知识点是一元二次方程,解题过程如下。
假设道路宽度为x,结合图形将6 块草地平移后组成一个长方形,那么它的长是50-2x,宽是30-x。已知每块草地的面积是50m2,6 块草地的面积之和是300m2,可列出方程(50-2x)(30-x)=50×6,化简可得x2-55x+600=0,求解得到x1=15,x2=40,结合题目将x2舍去,最终得到道路宽度为15m。
四、如何在教学中更好地渗透数形结合思想
(一)模仿实践,初步感受数形结合思想
数形结合思想刚开始应用在教学中,应该从简单的案例入手,让学生直观感受。例如,数轴可以描述有理数的绝对值,教师可以提出问题:互为相反数的两个数,它们的绝对值有什么关系呢?对于这个问题的解答,教师可以利用数轴上的点表示数,然后让学生模仿和实践,从而发现它们距离原点的距离相等,即绝对值相等。
(二)对比运用,深化理解数形结合思想
初步感受数形结合思想后,教师可在教学中运用对比方法,让学生进行深入理解。以函数为例,一次函数比较函数值的大小,通常结合函数的增减性即可做出判断。但是,反比例函数的图像不连续,是由两条曲线组成的。这时,教师可以让学生自己尝试,画出反比例函数的图像,然后区分象限进行考虑;如果在同一个象限,可利用增减性比较函数值大小。教师让学生对比尝试,借助图形解决问题,能加深其对数形结合思想的理解,以便其解题时灵活运用。
(三)独立思考,充分掌握数形结合思想
当学生对数形结合思想有了深入了解后,教师应作为引导者和管理者,发挥学生的主体作用,让他们通过独立思考,充分掌握数形结合的应用方法。一方面,教师可以利用一连串具有相关性的问题,引导学生培养观察、猜想、归纳能力,通过由数到形、由形到数的转化,提高数形结合思想的运用能力。另一方面,学习数学知识是为了解决实际问题,教师还应为学生创设真实的生活情境,让学生学会采用数形结合的思想去解决实际生活中的问题,从而简化解题步骤,提高解题效率[5]。
结 语
综上所述,数形结合是一种重要的数学思想,能激发学生的学习兴趣,提高学生知识记忆能力,培养学生数学思维。文章以实数、整式运算、坐标系、函数、方程等课程知识为例,结合例题介绍了数形结合思想在解题中的应用。在实际教学过程中,教师应考虑学生的实际情况,合理设计教学方案,让学生循序渐进地感受、理解、掌握数形结合思想,实现预期教学目标。

