一种水声弱信号奇异熵特征提取方法

叶博源，梁 喆，刘文帅，吕孟婷，宋建强

(大连测控技术研究所，辽宁 大连 116013)

0 引 言

在舰船目标识别的过程中，通常采用高阶谱、LOFAR谱分析等功率谱分析方法反映舰船目标的物理特性；采用ARMA模型法等现代信号处理方法提取舰船辐射噪声特征。由于海洋信道的复杂性，水声信号具有非高斯性、非线性、非平稳性的特点。因此，传统的信号处理方法不适用于水声信号处理。

HHT(Hilbert-Huang Transform)以傅里叶变换为基础，能自适应性地对线性稳态信号和非线性非稳态信号进行分析。

利用EMD方法的自适应分解特性可以得到多阶带宽不同的IMF，但如果按常规方法没有筛选的将前几阶高能量IMF分量直接重构后解调，可能因为被测舰船距离较远，辐射噪声掩蔽在环境噪声下，导致无法从能量较高的背景噪声中提取出有用的舰船辐射噪声。

本文基于EMD方法将信号分解后得到的多阶IMF经过熵值筛选后重构信号，将重构信号解调分析得到被掩盖在背景噪声中舰船辐射低频特征信号，改善对舰船远距离探测识别效果。

1 希尔伯特黄变换（HHT）

1.1 经验模态分解

设原始信号() ，首先确定()上所有的极值点，采用三次样条函数曲线对所有的极值点进行插值。从而拟合出原始信号() 的上包络线()及下包络线() 。取上包络线和下包络线的均值得到()：

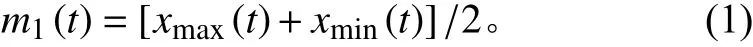
用原始信号减去均值得到()，即

重复计算式（2），直至第次提取出的信号()满足IMF条件，即

定义为第一阶IMF，即

将周期较短的IMF分量从原始信号中分离出来：

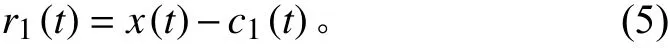
将余量()作为新的信号重复以上步骤，最终原信号可以表示为：

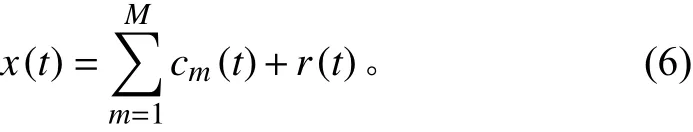
式中：c() 表示阶I M F分量，()为剔除所有IMF分量后的余量，为IMF总阶数。定义IMF终止门限为：

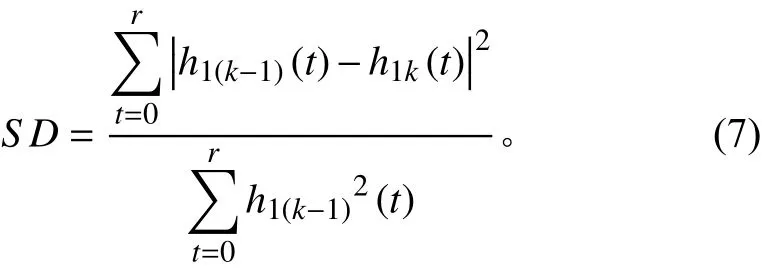
当0.2≤≤0.3时，停止筛选IMF分量。

1.2 解调谱分析

DEMON（detection of envelope modulation on noise）分析算法被广泛地应用于水声声呐信号分析过程中，其对接收的宽带信号采用平方解调、希尔伯特变换等方法以计算低频解调谱，包络信号为其解调后的低频时域信号，DEMON谱为其功率谱。

舰船螺旋桨在非均匀尾流中转动，会出现调制现象，通常将调制信号写为：

式中：为信号幅值，为调制幅度，ω为载波频率，Ω为调制频率。

一般来说，在各频带调制度相同的情况下，使用带宽越宽越有利于提高调制谱线谱的信噪比。但并不是使用宽带解调效果一定比使用窄带效果好，为了兼顾运算速率与解调谱的信噪比，通常在解调制运算前选取合适的带宽进行带通滤波，根据舰船特点，把宽频带分解成个子频带分别解调。但在识别系统中，目标通常处于未知状态下，常用的子频带分解经验不能有效地满足解调制谱运算需求。此时可以利用EMD方法的自适应特性，将原始信号分解得到多阶IMF分量，对IMF分量进行信号重构能得到合适的解调带宽。

图1 解调谱分析流程Fig. 1 Spectrum of demodulation on frequency analysis process

2 基于信息熵筛选IMF分量

常规的HHT方法中，通常默认前3阶IMF分量为能量较高且包含待测目标信息的信号，并直接采用前3阶IMF分量重构信号进行分析，但在实际实验中发现，当目标舰船距离较远时，信号的能量不一定集中在前3阶，且由于高频声衰减较快和EMD由高频向低频分解信号的问题，前几阶信号含有大量背景噪声，如果按常规方法没有筛选地将前几阶IMF分量直接重构后解调，辐射噪声会掩蔽在环境噪声下，导致无法从能量较高的背景噪声中提取出有用的舰船辐射噪声，降低舰船目标识别率。

信息熵是对信息进行量化的一个定义。观测系统越是混乱，信息熵就越高；观测系统越是有序，信息熵就越低。在一个无外部能量干扰的封闭系统中，熵总是增大，直至最大，因此必须有外部能量的干预才能使系统的熵减小。国内外已有大量将信息熵算法应用于机械故障诊断研究。

基于信息熵的特性，理想情况下把无舰船辐射噪声干扰的海洋背景噪声视为封闭系统，则水听器接收的信号为无序的白噪声，信号中包含信息量趋近无限，此时信息熵取最大值。当背景中加入船舶辐射噪声等人为机械噪声时，信号的无序性降低，信息量减少，信息熵的取值下降。将EMD分解得到的多阶IMF分量进行信息熵的计算，设置阈值，当熵值高于阈值，认为该阶IMF分量中存在大量无序噪声，即背景噪声过大，难以提取出舰船噪声特征。当熵值低于阈值，则认为舰船噪声特征占主要成分。

2.1 奇异谱熵

奇异值是矩阵酉对角化的扩展，比较稳定，在模式识别中有广泛应用。将声信号表示为可以反映原信号基本特征的奇异值集合，然后从该奇异值集合中提取信息熵，作为描述次声信号复杂程度的量度标准。奇异谱熵反映了在奇异谱划分下时间序列的分布模式，在信号信息量的评估及信息成分的分析等方面具有优良性能。

对采样信号x进行加窗处理，窗的长度为，设分析窗口的时延长度为1，通过加窗把信号序列x拆分成段序列，从而构造 (-)·维的轨迹矩阵。

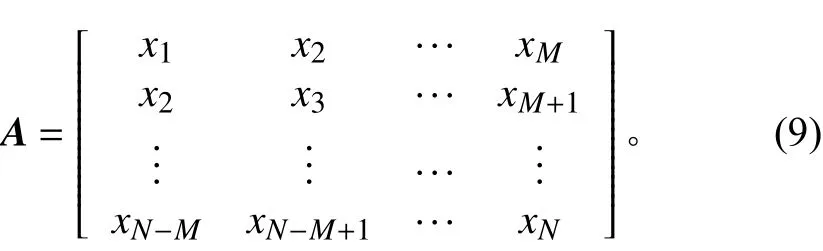
对矩阵进行主成分分析，得到一组奇异值δ≥δ≥···≥δ，将其组成向量δ，计算模式比为：

奇异谱熵值为：

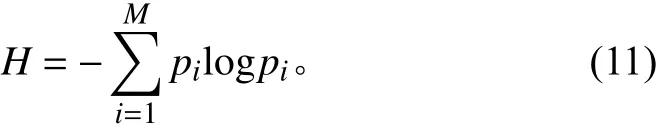
2.2 基于奇异谱熵值筛选IMF分量的重构信号

采用一段实验获取的舰船噪声信号进行分析，已知该船推进系统为单轴三叶桨，转速520 r/min，轴频为8.6 Hz，被测舰船与测量系统距离为2.5 n mile，图2为原始信号。

首先将信号进行EMD分解，得到各阶IMF分量，前6阶IMF分量如图3所示。

计算各阶IMF分量的奇异熵，结果如表1所示。

经过多次实验发现，选取用于重构信号的IMF奇异熵并非越低越好。虽然熵值越低代表信号有序度越高，但同时也表示信号的复杂性越低，然而舰船声辐射特性并非单频信号而是多种噪声结合形成的信号，若选取熵值过低会导致损失大量特征信息，同时增大低频噪声，使重构信号中出现大量舰船特征中并不存在的噪声。如果选取熵值范围为5～9，对应选取该信号4～6阶IMF分量，重构信号如图4所示：

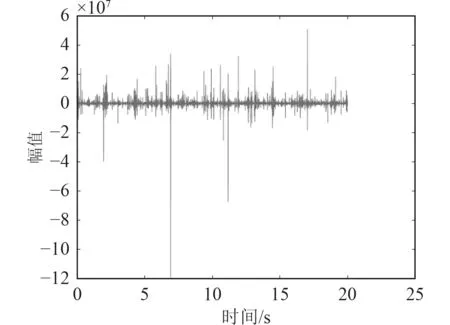
Fig. 2 Original signal

表1 各阶IMF分量的奇异值熵Tab. 1 Singular value entropy of IMF components of each order

对比图5中没有经过熵值筛选，直接选取能量较强的前3阶IMF分量重构信号，可以明显看出经过熵值筛选的IMF分量重构信号提取出了掩蔽在噪声下的8.6 Hz轴频信号。

对比图6中近距离对目标测量得到的高信噪比辐射噪声，可以看出经过熵值筛选的重构信号增强了由轴频及其谐波信号的基本特征线谱，相比图5中未经熵值筛选的信号，获得了更好的信噪比。

3 舰船目标识别试验

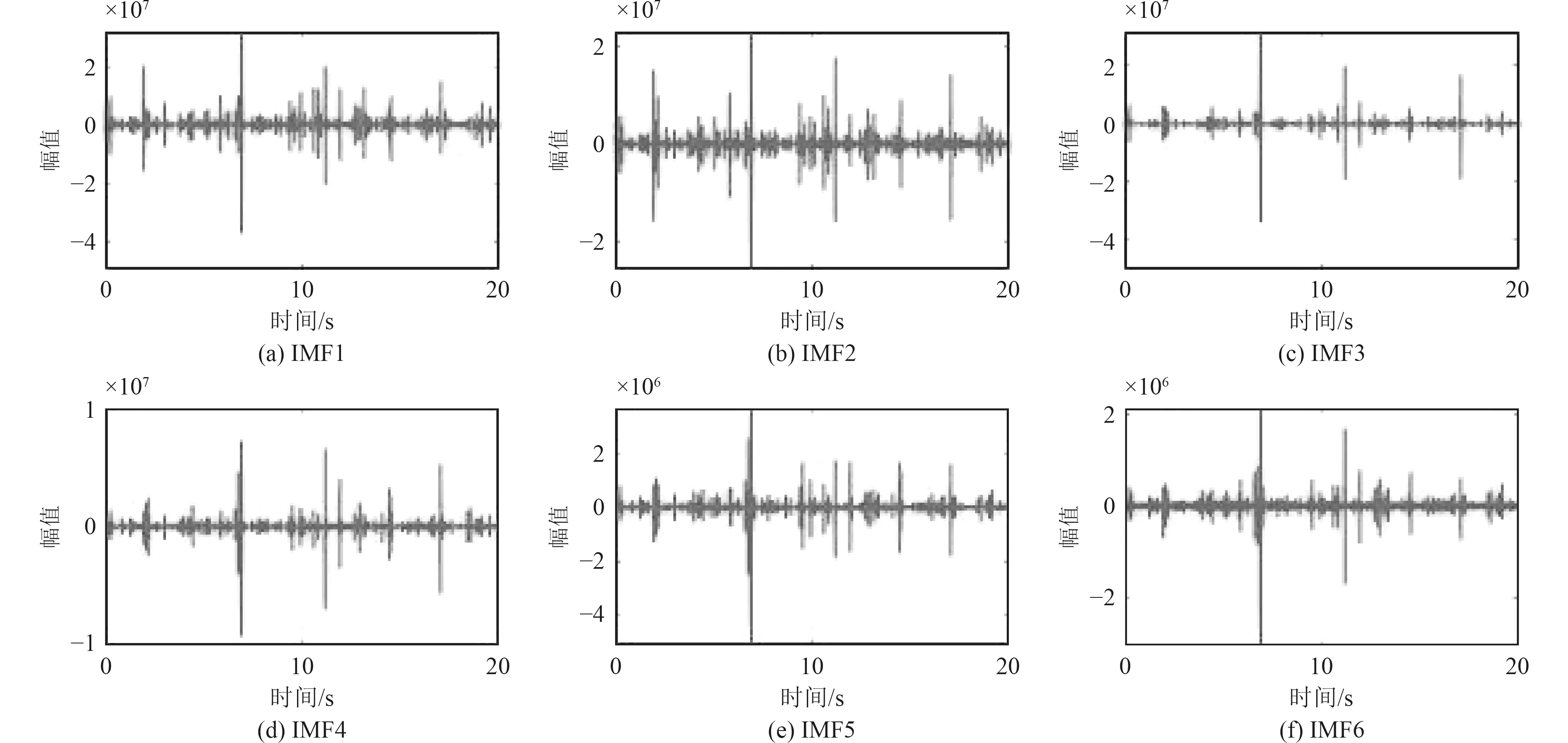
图3 各阶IMF分量Fig. 3 IMF components of each order

图4 4～6阶IMF重构信号Fig. 4 4～6 order IMF reconstruction signal

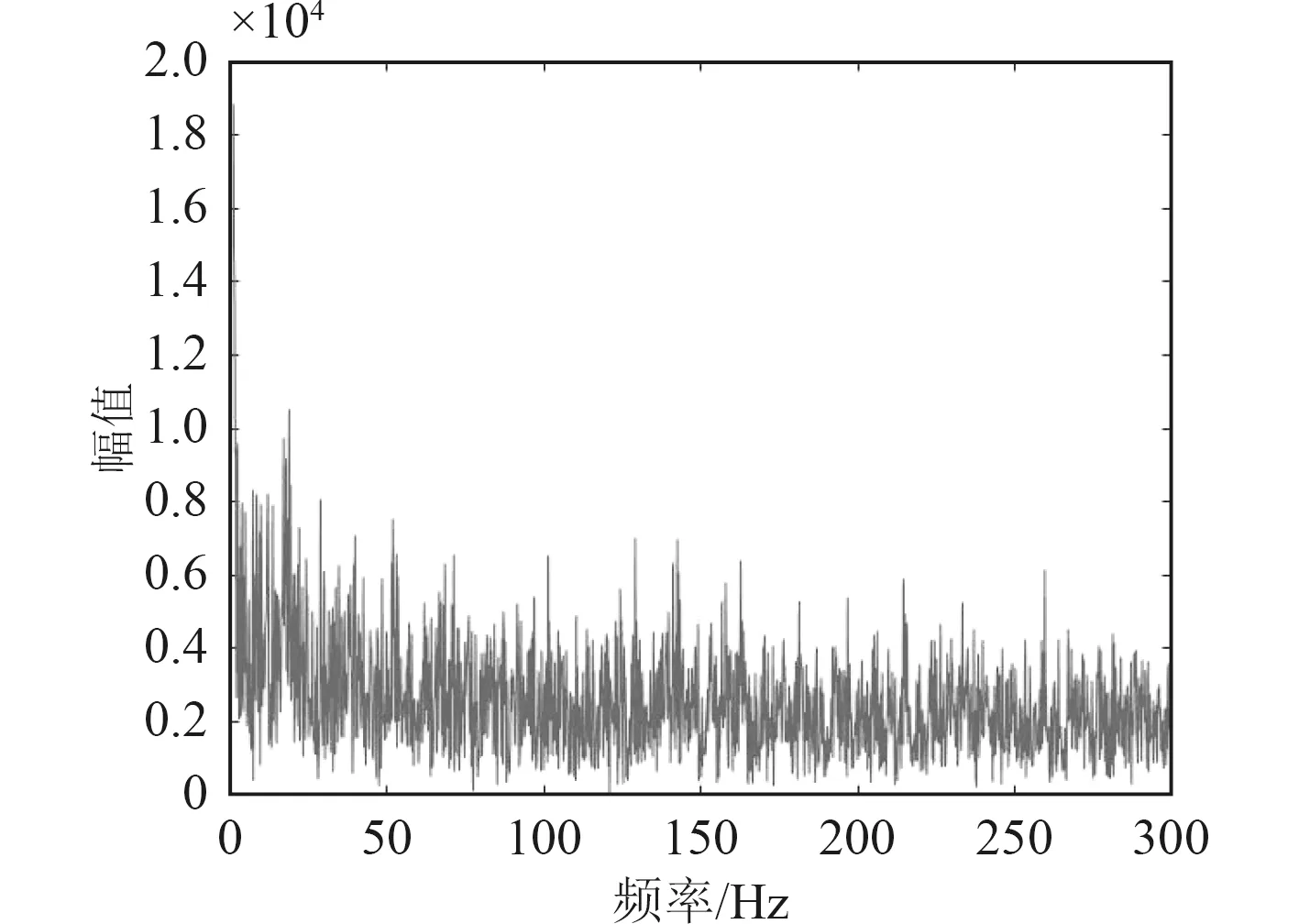
图5 1～3阶IMF重构信号Fig. 5 1～3 order IMF reconstruction signal

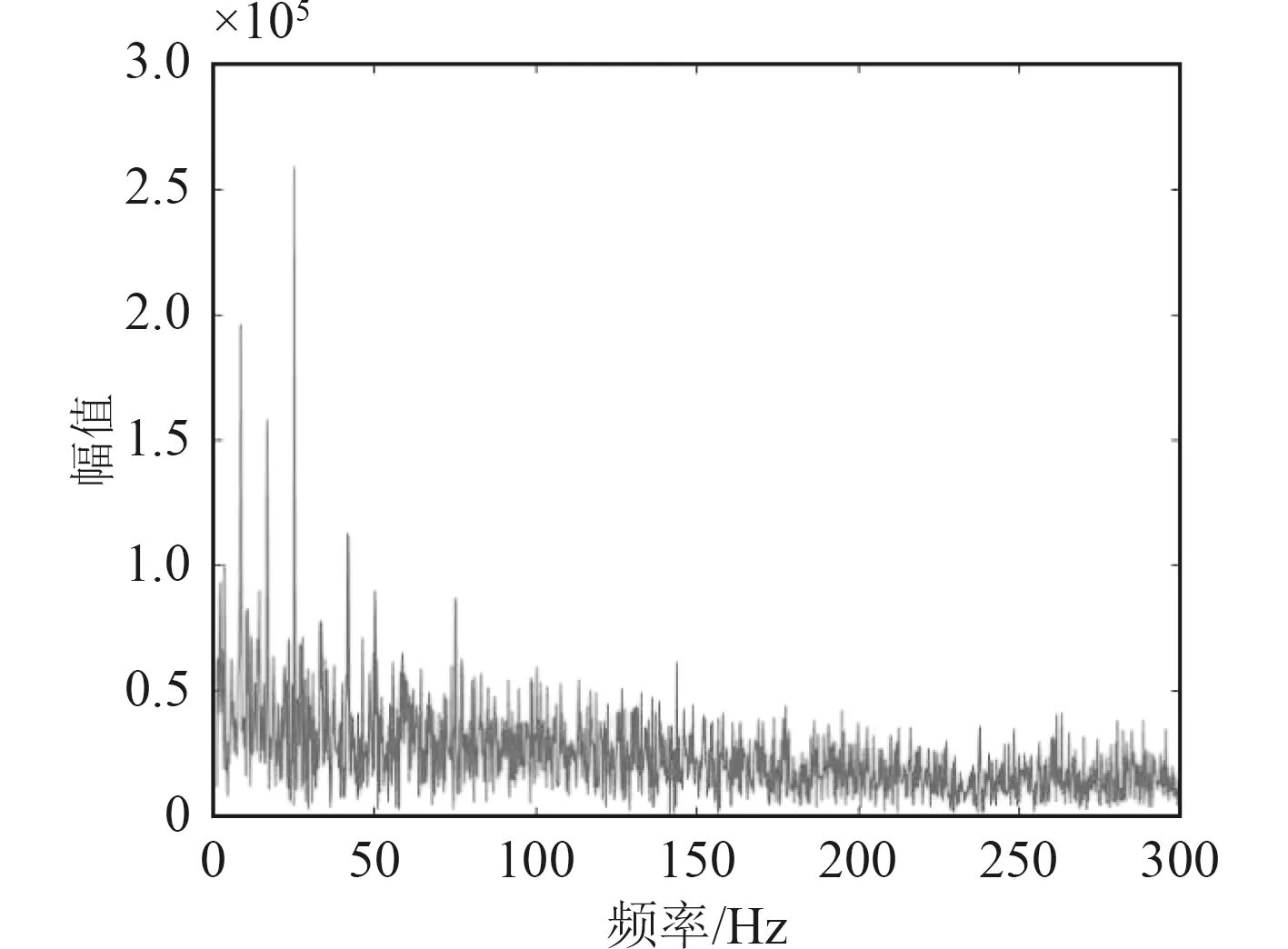
图6 近距离测量目标的辐射噪声特征Fig. 6 The measuring characteristics of radiated noise of targets at close range

实验采用一组目标舰船近距离测量得到的高信噪比特征数据作为训练组来训练BP神经网络，分别采用不对IMF进行筛选重构信号的常规方法和对IMF分量进行熵值筛选后重构信号的新方法，对100个距离为2.5 n mile匀速航行的目标信号和100个距离2.5 n mile转向机动的目标信号进行识别，得到识别结果如表2所示。

可以看出，将EMD分解得到的IMF分量经过熵值筛选后重构的信号可以提取出原本被掩蔽在环境噪声下的舰船特征信号，特别是目标处于远距离机动状态下，新方法对识别率的提升更为明显。

4 结 语

本文利用常用的HHT方法，对原始信号进行EMD分解得到各阶IMF分量，对各阶IMF分量进行熵值筛选后重构信号，再对重构信号进行希尔伯特变换，得到的结果用来作为对目标识别的输入信号。该方法提高了舰船辐射信号中一部分特征的信噪比，使其在神经网络中占据更大的权值，一定程度上提高了远距离对目标的识别率。但由于信息熵本身并非定量分析方法，难以从原理上分析得出最佳的熵值选择区间，由实验经验得出的结果容易导致应用范围较为有限。且实验中发现经过信息熵筛选的重构信号虽然对远距目标识别有提升效果，但目标处于近距离时，舰船辐射噪声的信噪比较高，高频部分衰减弱，对比远距声辐射总信息量增大，信息熵总体数值随之增大，如果继续以原数值范围进行筛选则会出现识别率无明显提升，甚至出现识别率下降等问题。后续将针对该问题继续研究不同工况和状态下舰船辐射噪声的熵值分布规律。

表2 对近距离目标的识别效果Tab. 2 Recognition effect on short-distance targets