基于混合粒子群算法的船用离心泵电机优化研究

付荣赫，邢吉生

(北华大学 电气与信息工程学院，吉林 吉林 132021)

0 引 言

离心泵作为船舶系统不可或缺的一部分，其在运行时起到了关键作用，进而对驱动电机的控制效果和性能等提出了很高要求。电机能否正常稳定运行，直接影响到离心泵能否稳定工作，进而影响到船舶各系统。因此，运用自动化技术和智能优化算法实现离心泵电机更加精确、稳定并快速的控制，提升离心泵的运行效率，具有非常重要的意义。

PID控制由于应用广泛，原理易懂，因而得到了普遍运用。PID控制器参数整定优化的结果对于离心泵电机的控制效果起决定作用，然而在传统PID参数整定过程中含有复杂棘手、难度大等缺点，传统方式很难在复杂系统中整定出理想的最优值，致使其控制效果不佳，不能满足系统的控制要求。

现如今，随着学者们对智能算法的深入研究，众多群智能算法被引入到PID参数整定优化问题中。但随着研究的深入，算法中的问题也逐步显现出来。比如PSO算法存在精度差、易陷入局部最优等问题。为此，本文提出一种将蝙蝠随机移动概念引入粒子群算法中来优化PID参数的方法，在保留算法简单、易实现的基础上，算法的精度、全局搜索能力等得到了显著提高，优化后的PID控制器能更好地达到系统的控制要求，且调节时间少、稳定性强，使得离心泵电机能够更加安全稳定运行。

1 PID控制

PID控制器由3部分构成，分别为比例、积分和微分等，一般形式下式：

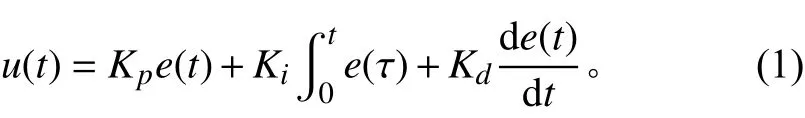
式中：为系统误差；K，K，K分别对应PID控制器中3个部分的系数，通过调整这3个系数，找到最优值，就能够得到最好的控制成果，达到改善控制性能的目的。PID的性能由这3个参数是否合理决定，所以，优化其参数具有重大意义。将式（1）转换为传递函数形式：

式中：T和T为其所对应的时间常数。

在众多的性能指标中，选用ITAE作为误差性能指标，一般形式如下式：

2 PID控制模型

2.1 船用离心泵电机研究

在船舶系统中，离心泵作为一种重要设备需向系统中输送水和油等液体，用于消防、抽水、排水等系统中，它是运用离心力的原理运行的，并将电机产出的机械能转换成被甩入液体的动能和势能。离心泵大致由泵体、叶轮、泵轴、轴承、密封环等构成，其结构如图1所示。

通电后电机获得电能并驱动离心泵运转，同时又要求电机在一定的环境下稳定工作。所以正确选择驱动电机是使得离心泵效率高并稳定运行的关键，需仔细探讨其性能和可靠性等因素。在实际使用中遭遇意外情况或故障时，对驱动电机的效率、调节时间等有着很高的要求，以达到能快速启停、增减速等效果。在众多的驱动电机中，永磁直流电机特点显著，因其损耗小，运行简便，便于控制，响应速度快，易调速等特性，将其用作船用离心泵的驱动电机。

图1 离心泵结构图Fig. 1 Structure diagram of centrifugal pump

2.2 电机传递函数

运用电机的机械特性和参数等，能简单并快速获取传递函数。与他励直流电机相比，永磁直流电机用永久磁体取代了励磁绕组，其电路图如图2所示。电磁转矩T和 感应电动势E是电机实现电能机械能之间相互转换的主要参数。电动机两端的电压值为U，R是电枢电路的电阻，电机的转速为，L是电枢回路的自感，M是粘性摩擦负载。

图2 永磁直流电机等效电路图Fig. 2 Equivalent circuit diagram of permanent magnet DC motor

永磁直流电机转速发生变化时，电磁转矩方程为：

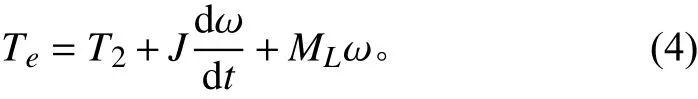
式中：T为电枢绕组在磁场中受力产生的电磁转矩；为输出转矩；为转动惯量；ω为角速度。

负载阻转矩方程为：

式中：C为 转矩常数；I为电动机电枢电流。

电枢电压方程为：

2.3 传递函数的确定

采用某型号永磁直流电机，将其参数代入式（7）中，可得传递函数为：

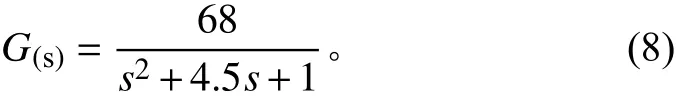
此系统为典型的2阶系统，对永磁直流电机控制系统的传递函数在Matlab软件中仿真，其在Simulink环境下其仿真图如图3所示。

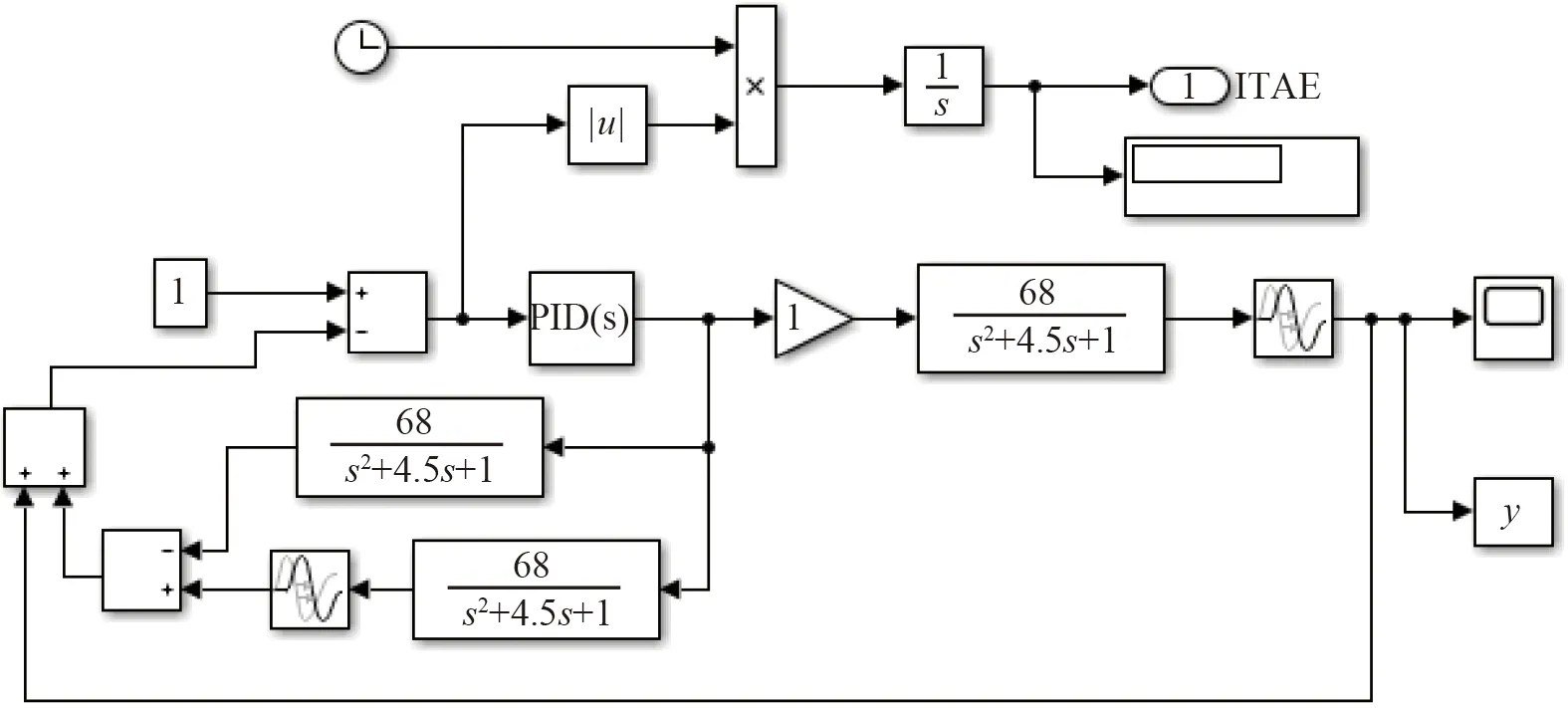
图3 Simulink环境下PID仿真图Fig. 3 PID simulation diagram under Simulink environment

3 智能算法

3.1 粒子群算法

粒子群算法（简称PSO）主要是运用粒子间的彼此配合，共享全局最优位置来搜寻待优化问题的最优解。该算法以所有个体的位置作为待优化问题的解，用适应度函数来计算粒子的适应值，通过将所有个体的适应值进行对照，判断粒子位置的好与坏。当所有个体在待优化问题解的空间中移动时，每次迭代中粒子的移动方向和距离由一个速度变量所决定。经过不断更新个体位置和最优位置，粒子在搜索空间中逐渐逼近最优位置。

粒子在搜索空间中的速度和位置由式（9）和式（10）来确定：

式中：为粒子位置，为粒子速度，为学习因子；,∈[0,1]， 其为随机数；ω为惯性因子，普遍取值为0.1～0.9；P为粒子的最好位置，为全体粒子群的最好位置。

运用PSO优化PID参数的大致流程如图4所示。

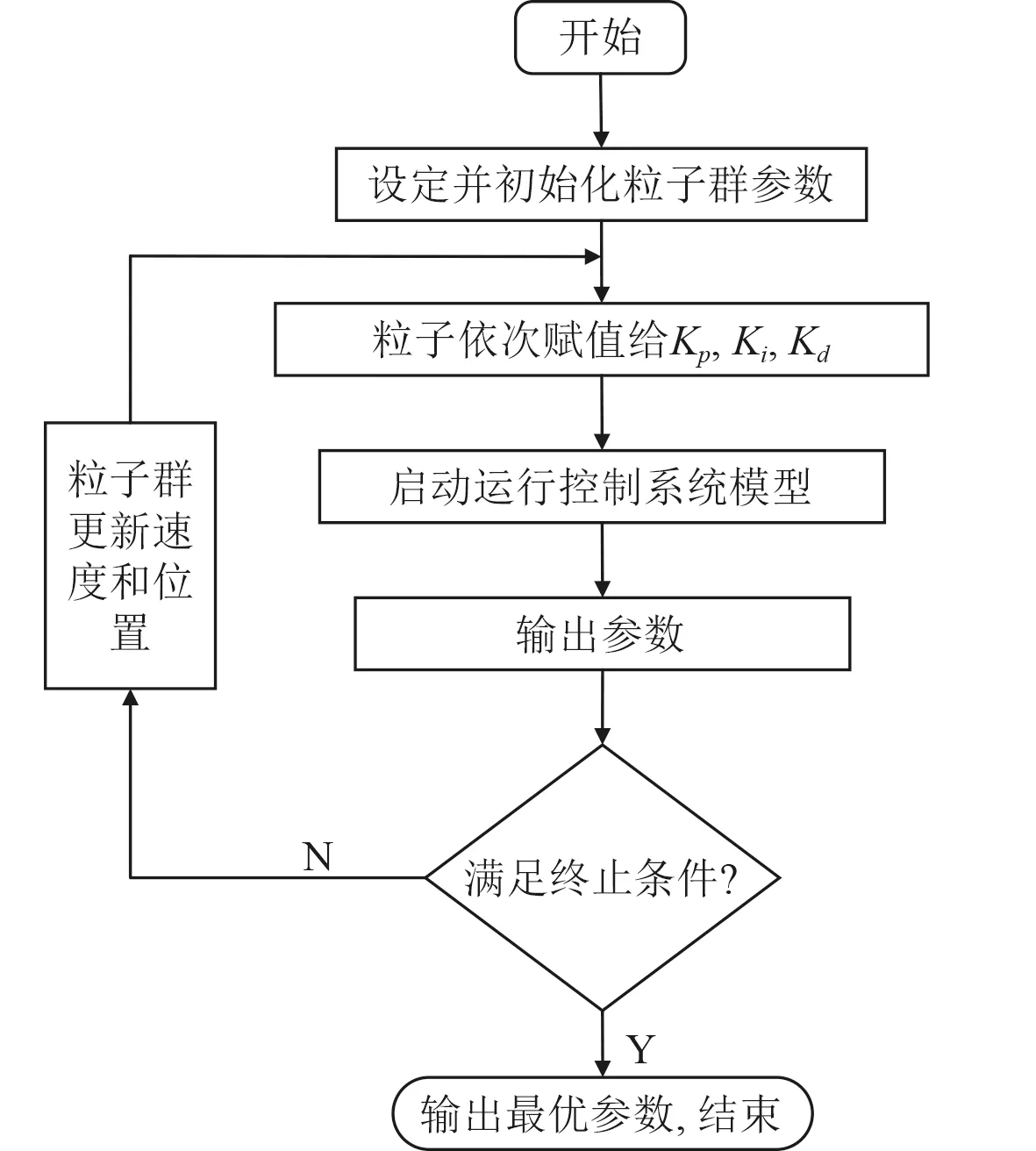
图4 PSO优化PID过程图Fig. 4 PSO Optimization PID process diagram

3.2 蝙蝠算法

蝙蝠算法（简称BA）是利用蝙蝠觅食时回声定位特性的一种群智能算法。其中，蝙蝠靠随机改变其速度、位置和超声波频率等来搜寻猎物。当它靠近猎物时，蝙蝠发出的超声波频率会加强，与此同时响度也会降低，表明距离猎物越来越近。效仿蝙蝠搜索猎物过程，运用式（11）更新其频率，运用式（12）更新其速度，运用式（13）更新其位置。

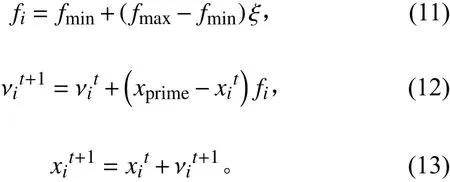
式中： ξ∈[0，1] ，为随机数；为频率变化的最小值，为频率变化的最大值；全局蝙蝠最优位置。

当确定了当下最优值后，每只蝙蝠按照式（14）做随机移动，进而产生一组新解。

式中：x为新的解位置，x为上一代的解位置；τ∈[-1，1] 为随机数；A为其响度在时刻均值。

3.3 混合粒子群算法（HPSO）

对于PSO存在容易陷入局部最优等问题，提出混合粒子群算法（简称HPSO）。将蝙蝠算法融入到PSO算法中，增强粒子多样性，并加强局部搜索能力。将蝙蝠算法里种群中的每个个体都可以描述成PSO中的粒子进行搜索，将算法里蝙蝠随机移动的概念引入到PSO中，对其位置进行更新，此方法可增强粒子位置的多样性。位置更新公式如下式：

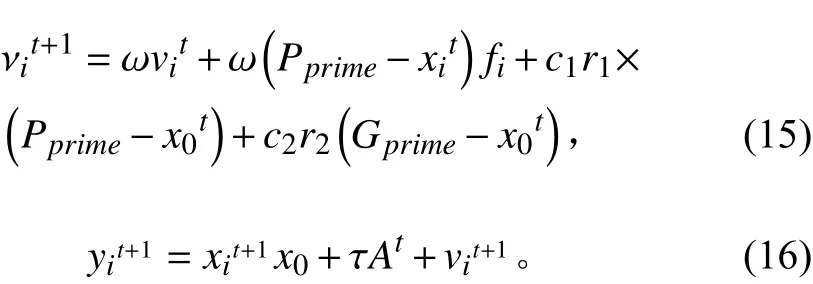
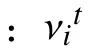
运用式（15）和式（16）进行反复迭代，通过反复更新粒子的位置，将其产生的新位置和目前的最优位置进行对比，找出最优解继续迭代，直至找出全局最优解，进而找到最佳参数值。

运用HPSO优化其参数的结构图如图5所示，其大致流程如下：

1 初始化参数。拟定粒子数目，K，K，K和惯性权重的范围，学习因子的值，音量参数值，设定最大迭代次数maxIter，然后将种群中所有个体的位置和速度初始化。

2 调用sim函数。把所有粒子的位置分量的值各自赋给K，K，K，启动系统仿真模型，得到性能指标，并输出每个粒子对应的适应值。

3 对粒子群的运动状态进行更新。运用式（8）重新更换其速度，运用式（9）重新更换其位置，判断其速度和位置是否越过了既定区域，若其越过，则用范围限值替换当前的速度或位置。

4 对于每个个体，把它的适应值和所有群体所经过的最佳位置的值相比，要是较好，便把它用作当前的。

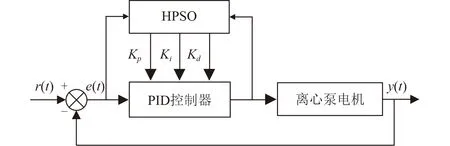
图5 HPSO整定PID参数控制图Fig. 5 HPSO tuning PID parameter control diagram

5 对于每个个体，把它的适应值和此粒子所经过的最佳位置P的值相比，要是较好，便把它用作当前的P。

6 引入BA算法中随机移动理念，运用式（15）和式（16）计算下一代的位置，更新和P。

7 判别其有没有达到结束要求。要是已达到，则输出最佳参数，即PID参数的最佳组合，要是没有达到，返回步骤3重新执行。

4 仿真结果与对比分析

分别选用HPSO，PSO和传统方法对系统进行PID控制器的参数优化。假设粒子数nop=30，迭代次数的最高值maxIter为100次，K，K，K位置搜索范围为[-10，10]，学习因子取值皆为2，惯性权重从0.9降低至0.2，音量参数为0.1，τ取值为1。

在图3的仿真模型中，其输入为单位阶跃信号，仿真时长设为10 s，采样时长d=0.001 s。多次迭代后其适应值收敛图如图6所示，输出其各参数如表1所示。

将3种方法优化所得的参数值代入离心泵电机控制系统的PID控制器中，并在Matlab中运行，得出响应曲线如图7所示。

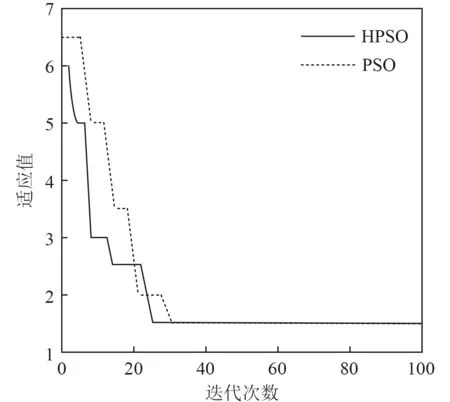
图6 适应值收敛曲线Fig. 6 fitness convergence curve

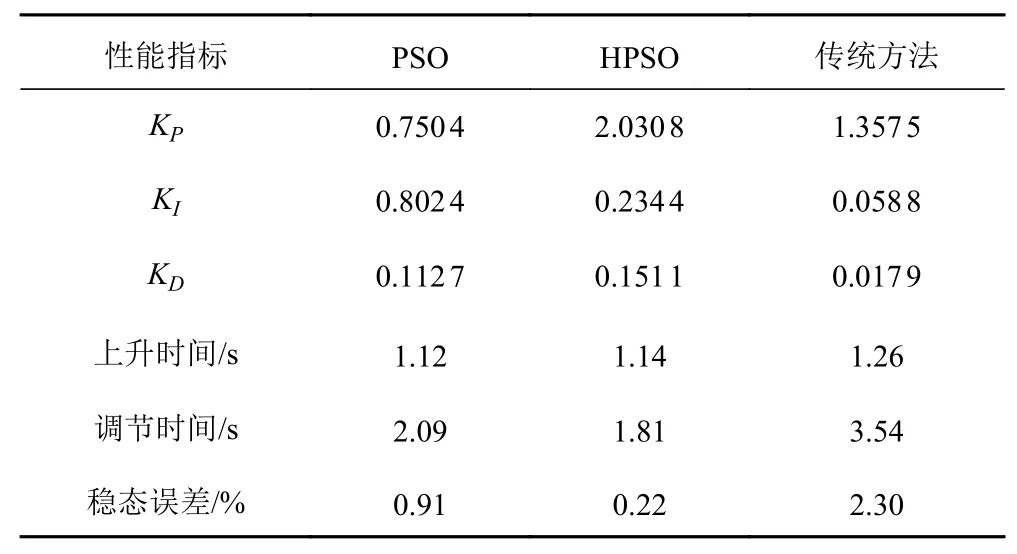
表1 PID整定优化结果Tab. 1 PID tuning optimization results

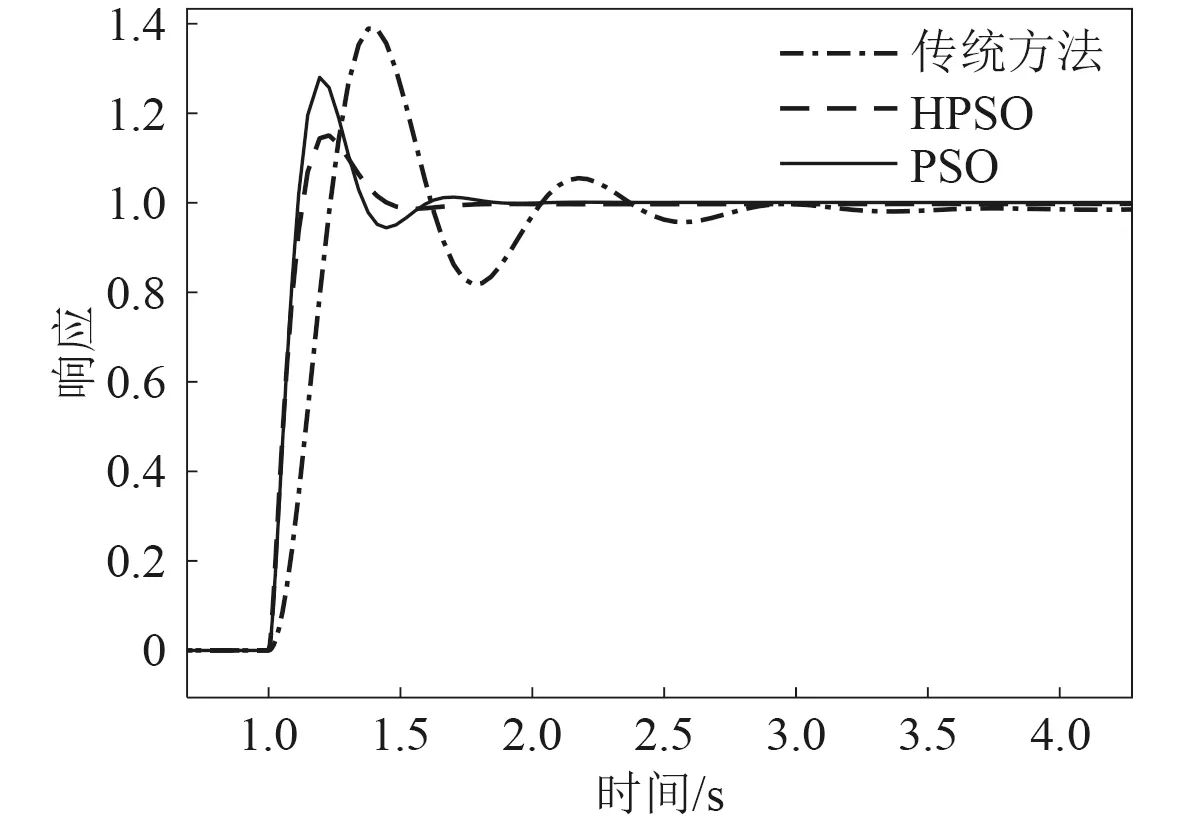
图7 系统阶跃响应输出曲线Fig. 7 System step response output curve

由图6可知，随着迭代次数的增加，HPSO在迭代次数为25次时适应值得到了收敛并得到了较高的精度，而PSO迭代到31次时适应值得到了收敛，因此HPSO展现出了收敛速度快、精度高等优势。由图7和表1可知，标准PSO的上升时间短，进而导致PSO的响应速度快于HPSO算法，但在超调量、稳态误差等方面HPSO明显更少。

HPSO到达稳定所用的调节时间为1.81 s，优于PSO稳定的调节时间2.09 s和传统方法的3.54 s，因此系统的调节速度更快，能很快达到稳定状态。经过HPSO优化的PID最佳参数，使其选出的3个值恰当，能够很好将调节时间和超调量等优化到尽可能少，使得系统能得到良好的控制效果，因而证明此方法的可行性。

5 结 语

本文以船舶离心泵电机为研究对象，常规PID控制存在稳定性能差、控制精度低等问题，提出运用HPSO优化PID参数的方法，并验证了引入蝙蝠随机移动概念后的HPSO算法通过增强粒子多样性能改善PSO易陷入局部最优等缺点的可行性。通过对比3种方法参数整定优化的结果，在控制效果、调节时间、性能指标和稳定性等方面，HPSO算法比其他2种方法效果更好，显著提高了系统的稳定状态，有效提升了离心泵电机控制系统性能和运行稳定性。