Toeplitz算子的双正规性和M-亚正规性

崔璞玉, 李 佳, 冯琳颖

(辽宁师范大学 数学学院，辽宁 大连 116029)

算子理论中正规算子的研究已经非常完备. 特别地, Toeplitz算子的正规性也有较完全的描述, 许多学者将正规性的概念推广得到拟正规性、M-亚正规性、双正规性等.

设H为无穷维复可分Hilbert空间,B(H)为H上一切有界线性算子所构成的Banach代数.T*表示T∈B(H)的共轭算子.如果T*T=TT*, 则T是正规的; 如果T*TT=TT*T, 则T是拟正规的; 如果T*TTT*=TT*T*T, 则T是双正规的; 若存在M>0, 使得对于所有的ω∈,f∈H有‖(T-ω)*f‖≤M‖(T-ω)f‖成立, 则称T是M-亚正规的.

在相关的文献[1-17]中, 可以看出大多是在Hilbert空间上研究双正规和M-亚正规算子的性质等相关内容, 在具体函数空间如Bergman空间和Fock空间上关于双正规和M-亚正规Toeplitz算子的符号特征的研究相对较少.

令η表示[0,1]上的概率测度.定义开单位圆盘上的测度v为记()为上的加权Bergman空间, 是由L2(,dv)中所有解析函数构成的空间, 显然有()是L2(,dv)的闭子空间.定义集合{τt}t∈[0,∞)为

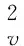
则其上的内积可以表示成

Tφ(f)=PB(φf),

其中,PB是从L2(,dv)到()的正交投影.

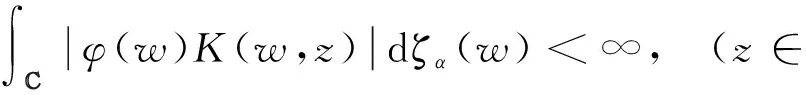
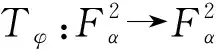
PF是从L2(,dζα)到的正交投影.

1 Bergman空间上Toeplitz算子的双正规性

定理1.1设φ(z)=eikθf(r)∈L∞(,dv), 其中,z=reiθ,k∈,f(r)是一个有界径向函数.Tφ为上拟正规的当且仅当满足以下条件:

(1)k<0,f=0;

(2)k=0;

(3)k>0, 且对任意n∈, 或者有f=0, 或者

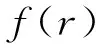
证对任意n∈, 有

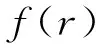
直接计算可以得到

另一方面,

设k<0, 当-k≤n<-2k时, 有

如果Tφ是拟正规的, 则有

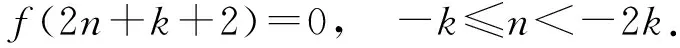
(1)

当n≥-2k时, 有

如果Tφ是拟正规的, 则

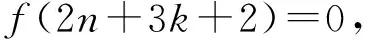
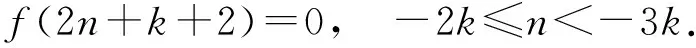
(2)

以此类推, 对任意n≥-k, 有

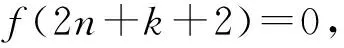
(3)

由式(3)可知f=0.

设k=0, 易得Tφ是正规的, 显然Tφ是拟正规的.

设k>0, 对任意n∈,

如果Tφ是拟正规的, 当且仅当

利用定理1.1中的方法可直接得到定理1.2.

定理1.2设φ(z)=eikθf(r)∈L∞(,dv), 其中，z=reiθ,k∈,f(r)是一个有界径向函数.Tφ在上是双正规的.

(1)n=0;

(2)n>0且a0=a1=…=an-1=0.

证首先证明充分性.若pn(z)=anzn, 则Tpn是单边加权移位算子, 则其一定是双正规的.

同样地，

对比上述两个多项式中z2n-1项的系数:

由此可见a0=0或a1=0.当a0≠0时, 继续依次对比各项系数

由此可见a1=a2=…=an=0与an≠0矛盾.

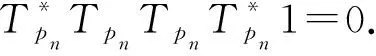
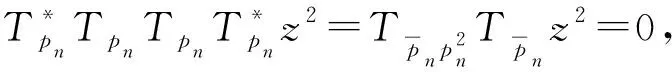
而

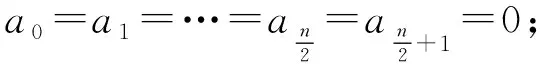
为了给出Bergman内函数与双正规Toeplitz算子之间的关系, 下面给出一个关于Bergman内函数的引理.

引理1.4设pn(z)=anzn+an-1zn-1+…+a0, 其中，n≥1,an≠0.则pn(z)为Bergman内函数当且仅当

证只需证必要性, 若pn(z)为Bergman内函数, 那么对任意zk,k≥1,〈pn(z),pn(z)zk〉=0.由计算可得

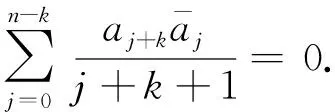
结合定理1.3和引理1.4可以得到下面的推论:

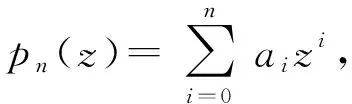
2 加权Bergman空间和Fock空间上Toeplitz算子的M-亚正规性

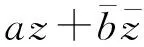
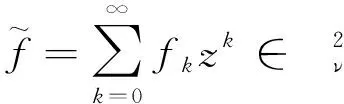
取f0=1,f1=0, 得

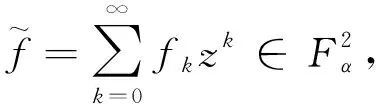
取f0=1,f1=0, 得