基于频繁子树模式的半结构化数据集聚类
李 巍,廖雪花,杨 军
(四川师范大学 计算机科学学院,四川 成都 610101)
0 引 言
大数据时代,基于海量数据的科学研究领域受到广泛关注并成为研究热点,例如大数据分析、深度学习和数据挖掘等[1]。大数据呈现出明显的半结构化特征,半结构化数据是使用树形Tree数据结构模型的各类数据总称,例如互联网HTML文档。半结构化数据具有自述性、标记性和动态性等特征而被广泛应用,Internet使用半结构化数据格式的HTML文档描述网页内容,并使用半结构化数据格式XML文档和JSON文档进行Web信息存储和信息交换,Microsoft公司使用半结构化数据格式Open XML存储Office办公软件docx、xlsx、pptx等文档,Redis和MongoDB等NoSQL数据库也使用半结构化数据格式存储Key-Value数据。
目前,半结构化数据聚类分析方法已经用于解决人们生产生活实际问题,例如,清华大学彭宗超等[2]在2020年新冠肺炎疫情期间基于网络大数据分析技术进行新冠肺炎疫情应急防控工作,Chitra等[3]使用XML聚类为Smarty Web搜索引擎建模等。
本文使用树形结构数据模型表示半结构化数据,提出一种以树形结构数据集频繁子树模式为特征的半结构化数据集聚类方法。首先,介绍树形结构数据集频繁子树模式挖掘方法和基于频繁子树为特征的聚类分析方法的理论背景。然后,本文提出一种基于模式增长策略的半结构化数据集频繁子树模式发现方法FSTPMiner,该方法使用编码树模型对树形模型数据进行线性编码,将树结构数据集频繁子模式挖掘转化为线性表频繁子模式挖掘,提高了树形结构数据集频繁模式挖掘效率。之后,使用频繁子树作为半结构化树形数据特征,基于余弦相似度Cosine Similarity计算方法和凝聚型层次文档聚类Hierarchical Clustering方法对半结构化文档数据集进行聚类。在ACM SIGMOD数据集、NASA数据集和人工生成数据集上进行对照实验,实验结果验证了本文半结构化文档数据集聚类方法在保证正确率的前提下,其聚类效率具有一定优势。
1 相关理论基础
1.1 含根有序标签树
半结构化数据文件由格式标记部分和文本内容部分共两个主要部分组成,可使用如文档对象模型DOM的含根有序标签树形模型表示,HTML文件的含根有序标签树DOM模型如图1所示。
树是一种非线性结构,是n个节点的有限集合,树的一般性定义如下:
定义1 树(Tree):树结构是无环连通图结构T={V,E,r}, 其中:V是有限非空节点集合,E是有限非空边集合,r是树的根节点。
根据树的不同特点和约束,可将树分为含根树和无根树、有序树和无序树、标签树和无标签树等:
(1)含根树与无根树:若树根节点r不为空,r∈V,即树含有一个可作为所有其它节点的祖先的根节点,称为“含根树”;若树根节点r为空,即无明确指定一个节点作为根节点,则称为“无根树”;
(2)有序树与无序树:若树中任意节点的孩子节点之间有顺序关系,这种树称为“有序树”。若树中任意节点的孩子节点之间没有顺序关系,则称为“无序树”;
(3)标签树和无标签树:若树中任意节点都带有一个标签Tag,标签Tag可用于区分不同的树节点,则称为“标签树”。若树中任意节点都没有标签,即不区分树中所有节点,则称为“无标签树”。
1.2 半结构化数据聚类方法
针对海量半结构化数据进行数据分析的基础工作是半结构化数据集聚类算法研究。由于数据集的半结构化特点,基于传统结构化数据集的聚类分析方法并不适用于半结构化数据集[3],所以很多研究集中在半结构化数据集高效聚类分析方法研究,这是很多领域需要解决的基础性研究问题。
半结构化数据集的聚类分析研究工作主要集中在两个问题的研究:第一是研究半结构化数据特征提取和半结构化数据间基于不同特征的相似性度量方法;第二是研究基于某种特征模式的半结构化数据集聚类分簇方法。国内外学者在半结构化数据集特征提取、相似性度量和聚类算法方面已经取得一些成果[4-6]。
在半结构化数据集频繁模式和特征挖掘方面,现有算法可分类两大类:
第一类是基于生成测试策略的方法,这种方法将半结构化数据频繁模式挖掘过程分为两个子过程,分别是候选子树集产生阶段和支持度产生阶段。例如Chen Y等[7]提出使用生成测试策略的基于Cuts检查树间包含关系的方法。
第二类是基于模式增长策略的方法,这种方法采用结果集增长策略并反复迭代直至结果集是频繁子树完备的。国内外学者在半结构化数据集聚类算法方面取得一些成果[8-12]。
2 半结构化数据集频繁子树模式挖掘
2.1 频繁子树模式挖掘策略
在半结构化数据集频繁子树模式挖掘过程中,关键内容和主要计算开销是半结构化树形结构数据之间的差异比较和相似性度量。半结构化数据的差异比较和相似性度量本质是图形结构数据Graph Structure Data的节点匹配问题。一般来讲,这类图形结构数据匹配问题涉及节点数量较大,图中路径较多,计算成本较大。以半结构化XML文档数据为例,根据X-diff算法[13],两个XML文档的差异比较算法的复杂度为式(1)
(1)
根据X-diff算法,两个半结构化数据之间的差异计算复杂度与树形结构的节点规模正相关。
因此,本文创新点在于提出并采用以下3个策略提高频繁子树模式的挖掘效率:
策略1:采用线性编码重建树结构数据。本策略的实现过程称为编码树构建过程,该过程采用线性编码树模型描述半结构化数据,通过增加额外编码信息,降低树形结构数据集的遍历计算开销,将复杂度较高的树形结构数据节点匹配和差异比较过程转换成线性表结构的差异比较过程,这样提高频繁模式挖掘效率。
策略2:降低半结构化数据集规模。本策略的实现过程称为数据集剪边过程,该过程在遍历已编码的树形结构数据集时,删除不可能在频繁子树集中出现的频度小于阈值的所有边。由于不频繁出现的边被删除,将会把一棵规模较大的树形结构数据拆分成多棵规模较小的树形结构数据。在该剪边过程结束中,如果出现单节点树结构,则将所有单节点树删除。
策略3:采用模式增长策略。本策略的实现过程称为数据集压缩过程,该过程基本思想是反复迭代遍历半结构化树形结构数据集,在每次遍历过程中,合并具有最大频繁度的相邻节点,直至满足停止条件。该策略优点是每次遍历都减小数据集规模,提高挖掘效率。
3棵示例半结构化数据建模的树形结构数据T1、T2和T3如图2所示,阐述在树形结构数据集中挖掘频繁子树模式的过程(FSTPMiner)。在频繁子树发现过程中,假设用户设定的最小频繁度阈值为2,也就是挖掘发现在数据集中出现次数大于等于2次的所有子树。
2.2 构建编码树
频繁子树挖掘FSTPMiner方法首先构建编码树,编码树是节点带有编码链信息的树形结构数据,编码链是一种链表结构,可以表示一颗含根有序标签树。

例如,图2中树T1的所有节点采用编码链结构表示后,如图3所示。
编码链本质是保存含根有序标签树频繁性质的链表结构,通过记录每个树节点在链表结构中的位置,以及其到父节点的距离,可与一棵含根有序标签树相互转换。通过编码链方法,可将含根有序标签树形结构数据集的频繁子树模式挖掘转化成线性表结构数据集的频繁子模式挖掘。
定义3 编码树(coding tree,CT):编码树定义为无环连通图CT={V,E,CL,L,F,r}, 其中V是树结构的节点Vertex非空集合、E是树结构的边Edge非空集合、r是树结构的根节点Root、CL是树结构的编码链非空集合、L是树结构的各个节点v到编码链cl映射的集合v→cl(其中,v∈V,cl∈CL)、F是遍历树时存储边频繁度的集合。
编码树是每个节点都带有编码链的树形结构,因为每个编码链都可表示一颗无序树,所以编码树可以被压缩,即将所有孩子节点压缩进编码链中。
根据定义2和定义3,将图2中树T1、T2、T3构建编码树后如图3所示。
2.3 剪边与压缩
构建编码树后,进行数据集剪边操作和迭代压缩操作。
定理1 在频繁模式集中,所有子模式树枝的频繁度都大于等于频繁度阈值。
证明:根据频繁模式定义,所有子模式出现的次数均大于等于预定义的最小频繁度阈值,所以所有子模式树枝的频繁度也大于等于预定义的最小频繁度阈值。证毕。
根据定理1,进行剪边操作。具体操作方法是将编码树中小于最小频繁度阈值的树枝删除,然后删除只有单节点的结构。
剪边操作后进行压缩操作。压缩操作具体方法是反复迭代数据集,在每轮迭代过程中,将当前数据集中出现次数最多的树枝进行压缩操作,压缩操作将树的两个节点合并成为一个点,同时,在这个合并后的节点的编码链上更新压缩后的内容。
图2中树形结构数据集T1、T2和T3经过构建编码树后,其2轮剪边与压缩迭代变换过程如图4所示。
经过第1轮迭代,剪边压缩后的数据集如图4(a)所示。此时,所有频繁度为3的边都已经被压缩,即 (3,4)(3,5)(3,6)和(3,7) 这4条边压缩成节点3141526374。经过第2轮迭代,剪边压缩后数据集如图4(b)所示,此时,所有频繁度为2的边也已经被压缩。每轮压缩后,都会将具有一定频繁度(即一定的出现次数)的边压缩进节点的压缩链中,例如,第1轮迭代压缩所有出现3次的边到编码链中,第2轮迭代压缩所有出现两次的边到编码链中。
因为用户设定的最小频繁度为2,所以经过两轮迭代剪边与压缩,最后得到的编码树就是频繁子树模式集,如图4(b)所示。之后,根据编码树定义,将图4(b)所示的所有编码树转换为含根有序标签树结构数据,最终得到的树形结构数据集就是出现次数大于等于阈值两次的所有频繁子树模式。
2.4 频繁子树模式挖掘方法
结合构建编码树过程和剪边压缩过程,半结构化数据集频繁子树模式挖掘过程方法FSTPMiner的伪代码描述如下:
频繁子树挖掘FSTPMiner算法
输入:半结构化树形结构数据集D={T1,T2,…,Tn}, 频繁度阈值e。
输出:频繁子树模式集F
(1) 为树集D构建压缩树集CD={CT1,…,CTn};
(2)MaxFrq=MaxE(CD); //将最大的边频繁度MaxE(CD)赋值给变量MaxFrq
(3) FOR 每个编码树CT=(V,E,CL,L,F,r)∈CD//步骤(3)为剪边操作
(4) FOR 每条边(x,y)∈E//E是树边集合
(5) IF EFrq(x,y) (6) IF 节点y是单节点 THEN 删除y; (7) ELSECD=CD∩以y为根的树; (8) IF |V|=1 THEN 在CD中删除CT; //V是树节点集合 (9) WHILEMaxFrq≥e; //压缩操作 (10) FOR 每个CT=(V,E,CL,L,F,r)∈CD (11) FOR 每条边(x,y)∈E (12) IF EFrq(x,y)=MaxFrqTHEN 压缩边(x,y); (13)MaxFrq=MaxFrq-1; (14)F←频繁FK项集对应的子树; //将频繁子树放入结果集F; 本文聚类过程将每个半结构化数据使用其包含的频繁子树作为特征,并组成相应的特征向量。然后使用余弦定理计算特征向量间的相似程度。最后的半结构化数据集聚类过程采用经典凝聚型层次聚类方法。 之后,使用余弦定理计算特征向量间的相似程度,设两个半结构化文档的特征向量分别为Fi和Fj,则Fi和Fj的相似度Sim(i,j) 计算方法如式(2)所示 (2) 最后,使用凝聚性层次聚类方法并根据半结构化文档数据集的特征向量进行聚类,过程如下: 基于频繁子树模式的半结构化数据聚类算法 输入:半结构化文档数据集D,最小频繁度e,层次聚类停止簇数阈值k 输出:聚类结果 (1) 计算半结构化文档数据集D的频繁子树模式集FP=FSTPMiner(D); (2) 对数据集D中每个半结构化文档构建特征向量 (3) 计算特征向量两两间的相似度并组成相似度矩阵Mm×m, 其中, 矩阵第i行第j列元素Mij值计算如下 其中,i=1,2,…,m-1,j=i+1,i+2,…,m; (4) 在Mm×m中查找具有最大值的元素Mij, 找到具有最大相似度两个簇i和簇j, 将这两个簇合并成新簇Cnew; (5) 计算新簇Cnew与其它簇的相似度, 更新相似度矩阵Mm×m; (6) IF 簇数量>kTHEN 执行步骤(4) ELSE return 簇信息; 本文相关实验均在主频为2.83 GHz 4 Core CPU、8 GB DDR4 2666MHz RAM的计算机上运行,操作系统为Fedora Core 6。 本文算法和其它相关对照算法均使用C++语言编写实现,在代码中使用C++ STL标准库容器和函数。解析XML文档DOM数据并处理树形结构数据使用TinyXML第三方开源库。 实验使用半结构化XML文档数据集,包括真实半结构化文档数据集和人工半结构化文档数据集。真实半结构化数据集来自ACM提供的SIGMOD标准XML文档聚类数据集和美国航空航天局NASA提供的航天飞机组播数据抽样半结构化数据集。人工数据集使用IBM XMLGenerator工具生成,共使用10个DTD文件,然后根据每个DTD文件随机生成100篇XML文档,因此人工数据集中共包含XML文档1000(10×100) 篇。 在上述软硬件实验环境中,实验过程分为两阶段: 第一阶段,基于人工生成的半结构化数据集,使用本文提出的半结构化数据聚类算法与刘昕等提出的基于局部密度的快速文本聚类算法[14]进行对照分析。该阶段实验目的是验证普通文本聚类方法在半结构化文档数据集环境中的适用程度; 第二阶段使用本文算法与其它已公开发表的半结构化文档数据聚类算法进行对照分析,对照算法包括Costa等提出的基于贝叶斯概率主题模型的XML文档聚类算法[9]、LIU等提出的ICQB算法[12]和Damalagas提出的经典半结构化文档聚类算法[10],这些算法是不同时期和不同应用环境下的半结构化文档数据集的代表性聚类分析算法。 在聚类实验过程中,频繁子树出现次数设定为3次(即频繁度阈值为3),所有凝聚型层次聚类过程停止条件阈值为k=10。 为测试普通文本聚类方法在半结构化文档数据集聚类环境中的适用程度,并验证普通本文聚类方法与针对树结构的聚类方法在半结构化数据集中的聚类效果,使用本文基于FSTPMiner的半结构化数据聚类算法与基于局部密度的快速文本聚类算法,基于人工生成的半结构化文档数据集,进行文本聚类对照分析。 聚类结果主要指标数据见表1。 表1 本文方法与文本聚类方法对照结果 分别使用基于FSTPMiner算法、Costa算法、ICQB算法和Damalagas算法对人工生成的半结构化XML数据集进行聚类,聚类结果正确率、召回率和聚类过程时间值见表2。 表2 人工数据集聚类结果 对于ACM SIGMOD真实数据集和NASA真实数据集,分别使用本文基于FSTPMiner算法、Costa算法、ICQB算法和Damalagas算法进行半结构化XML文档数据集进行聚类,聚类结果正确率和召回率见表3。 表3 真实数据集聚类结果 对于相同数据规模的半结构化数据集,使用聚类过程消耗的时间来衡量各个算法的聚类效率。在真实数据集对照实验中,本文基于FSTPMiner的算法、Costa提出的算法、ICQB算法和Damalagas提出的算法的运行时间见表4。 表4 真实数据集聚类时间 基于人工生成的半结构化数据集,经过本文针对半结构化树形结构数据聚类算法和普通文本聚类算法对照实验结果,可以得到以下结论: (1)本文针对半结构化数据树形结构特点设计的聚类算法,其聚类效果要优于普通文本聚类算法,在实验中,聚类结果的正确率提高25.3%,召回率提高20.5%; (2)半结构化数据聚类算法的聚类过程时间占用和内存空间占用要大于普通文本聚类算法,原因在于树形结构模型的解析和存储均大于文本线性模型。 对于各种半结构化数据集聚类算法,经过在真实半结构化数据集和人工生成半结构化数据集的各聚类算法对照实验运行结果,可得出以下基本结论: (1)本文基于FSTPMiner算法保证聚类结果正确率前提下,在半结构化数据集聚类效率方面具有优势。由于FSTPMiner算法使用半结构化数据集频繁子树模式作为数据特征进行聚类,这样①减少了数据集树节点总数,②避免了高时间消耗的树形结构数据差异比较过程,节省聚类时间,提高聚类效率,实验中相比于Costa算法,聚类效率提高39.97%; (2)根据各算法对照实验,基于FSTPMiner算法聚类结果的正确率和召回率略略低于Costa提出的算法,根据实验,在NASA数据集中,聚类结果正确率和召回率比Costa方法分别低0.2%和0.2%。原因是FSTPMiner算法仅使用半结构化数据集频繁子树模式作为特征进行相似度计算,虽然提高聚类效率,但忽略了非频繁模式的相似度信息。 综上所述,①一个含根有序标签树结构数据可以采用某种标签线性表结构表示,并且采用线性表结构的计算效率更优,该思想可以推广到其它树形结构数据的应用领域;②对于其它类型的树形结构数据,其线性化方法有待研究;③经典数据挖掘的剪边思想在半结构化数据挖掘领域依然有效。 为有效挖掘半结构化数据集频繁子树,本文提出频繁子树挖掘FSTPMiner算法,FSTPMiner算法基于编码树结构,采用剪边压缩动态策略在半结构化数据集中高效地挖掘频繁子树模式,进一步提出使用频繁子树为特征的、基于凝聚型层次聚类过程的半结构化数据集聚类方法,最后经过在真实半结构化数据集和人工生成半结构化数据集的对照验证实验结果表明:①与文本聚类方法相比,本文基于FSTPMiner方法聚类正确率等指标提高幅度较大;②与其它半结构化数据聚类方法相比,本文基于FSTPMiner方法在聚类结果基本不变的前提下能有效提高聚类效率。 下一步可以研究结合半结构化数据子结构和子内容的频繁子模式挖掘和聚类工作,也可以研究基于频繁子树模式的半结构化数据分类问题。3 相似度计算和聚类
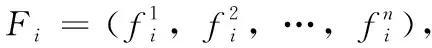
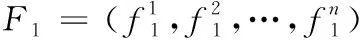
4 实验结果与分析
4.1 实验环境
4.2 实验过程
4.3 文本聚类算法对照实验

4.4 人工半结构化数据集实验结果

4.5 真实半结构化数据集实验结果


4.6 实验结果分析
5 结束语

