受迫振动法测量液体黏度

杨泽斌，洪玲儿,彭 力,2，刘朝辉

(1.华南师范大学 物理与电信工程学院，广东 广州 510006；2.华南师大(清远)科技创新研究院有限公司，广东 清远 511517)

测量黏度的方法有落球法[1]、旋转法、振动法等，其中振动法利用物体的振幅和周期的变化规律测量液体的黏度，该方法具有响应快[2]、测量方便等优点. 文献[3]利用小球在液体中做欠阻尼振动来测量液体黏度，但需找到与液体黏度适配的弹簧，否则会因欠阻尼数据不清晰而产生较大的拟合误差. 文献[4]用强迫振动扭摆法测量黏度较大的液体，但需先对已知黏度的标准样品进行标定后才能获得待测液体的黏度. 文献[5]用电机驱动钢球在待测液体中做受迫振动来测量液体黏度，但该方法受电机的限制，且在低电压时由于提供的驱动力变小，从而会导致测量误差变大.

本文利用磁动式扬声器提供周期性驱动力使小球做受迫振动，将实时图像采集和虚拟仪器测量技术相结合，测量液体黏度. 该方法操作简单，可一键生成实验结果，测量效率高. 通过该方法测量出甘油的黏度随温度以及质量浓度的变化曲线，并得到其经验公式.

1 基本原理

如图1所示，将小球通过轻质杆与劲度系数为k的弹簧相连，由于小球受重力作用，通过磁动式扬声器的驱动柱给予弹簧竖直向下的周期性驱动力F0cos (ωt)，由牛顿第二定律以及斯托克斯定律[6]可得小球的动力学方程为

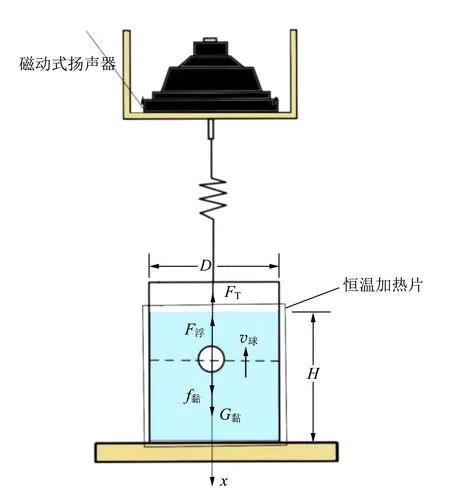
图1 测量原理图

(1)

该微分方程符合受迫振动动力学方程[7]，可解得：

(2)

其中，m为小球质量，d为小球直径，η为液体黏度，ω0和ωm分别为弹簧振子固有角频率和共振角频率.

考虑到斯托克斯定律的成立条件以及在小球振动过程中其周围流体会存在运动，可能出现湍流现象，需要对式(2)进行二级修正,最后可得待测液体的黏度为

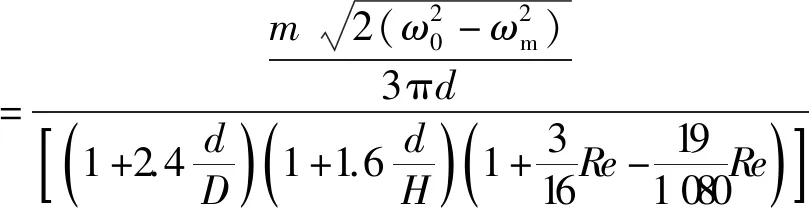
(3)

其中:D为容器直径，H为液体高度，Re为雷诺系数.

2 实验装置

图2为实验的整体装置图，由驱动装置和测量装置构成，通过驱动装置驱动小球在液体中做受迫振动，由测量装置对小球的运动进行追踪，得到小球在竖直方向上做受迫振动的相对位移-时间图像，分析图像可确定出液体的黏度.

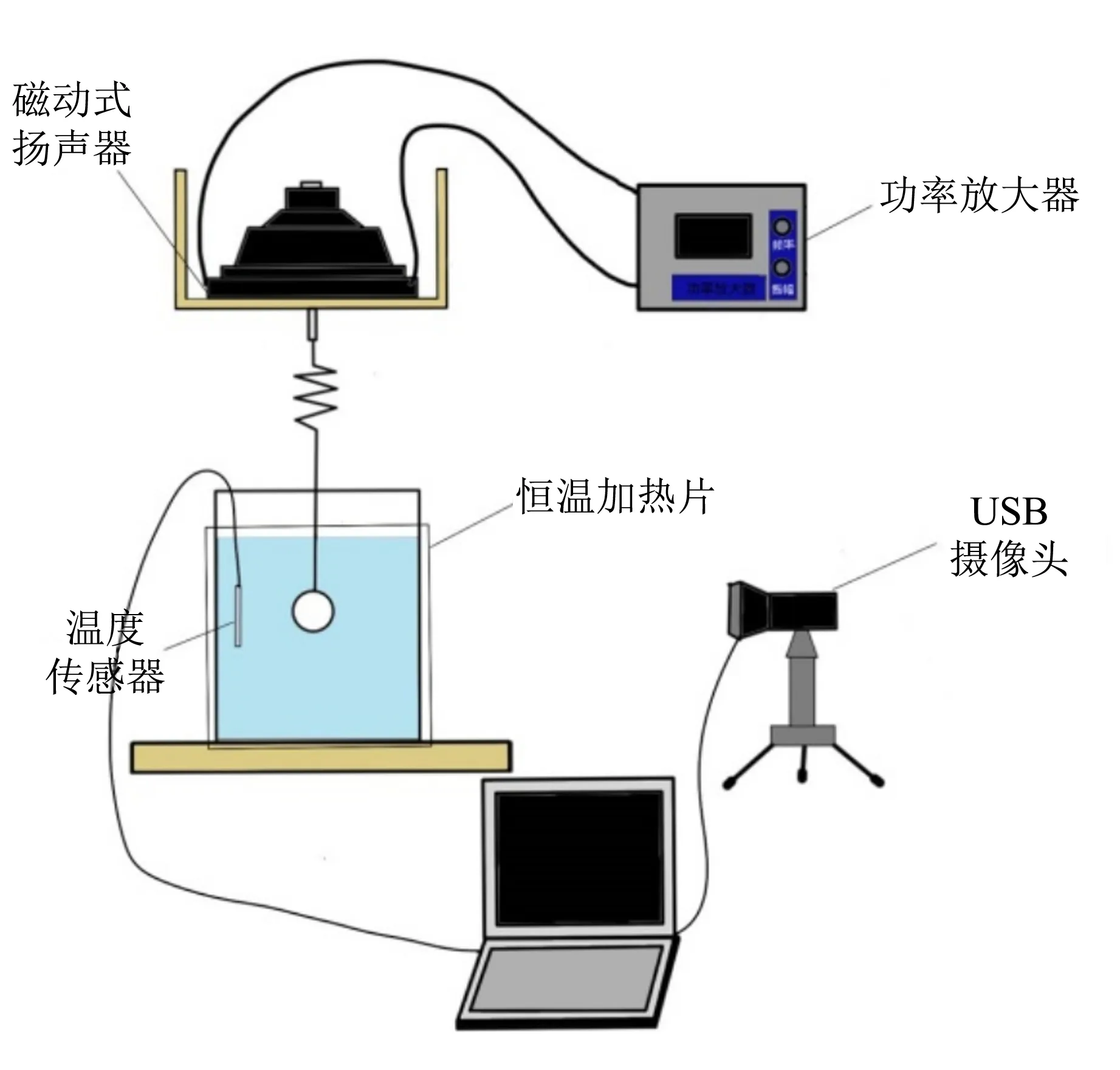
图2 整体装置图

2.1 驱动装置

驱动装置由功率放大器、磁动式扬声器和驱动柱组成. 功率放大器接通220 V交流电，可以为磁动式扬声器提供频率、振幅可调的正弦信号，磁动式扬声器通过驱动柱为弹簧振子提供竖直方向的周期性驱动力.

功率放大器有频率调节旋钮和振幅调节旋钮. 通过调节频率旋钮，可以使得弹簧振子达到共振状态. 调节振幅旋钮改变F0的大小，可以让弹簧振子的振动速度适合(既不会出现湍流现象，又利于摄像头采集图像)，从而减小实验误差. 由于没有湍流,对于式(3)可近似取Re=0.

图 3为实验测出的驱动柱在不同频率下的轨迹图，从图3可看出：当频率发生改变时，振幅基本不变. 因此，驱动柱可以提供较好的周期性驱动力.

图3 不同频率下驱动柱相对位移-时间图

2.2 测量装置

测量装置为USB摄像头，内置自主设计的测量程序. 将实时图像采集和虚拟仪器测量技术相结合，实现了数据测量、数据分析、数据处理一体化. 通过USB摄像头对小球的振动图像进行采集，通过测量程序进行图像分析和目标追踪，并实时显示出小球在竖直方向上的相对位移x和时间t的图像，再经过分析处理即可得出弹簧振子的振动角频率ωm. 图4所示为测量程序基本流程图.

图4 测量程序流程图

由于摄像头监测的灵敏度较高，并且通过目标追踪程序实时显示小球的运动情况，可以直观地获得小球的振幅，有效减少判断小球最大位移处所引起的偶然误差. 通过选择对应的小球振动周期即可一键显示小球的共振频率和待测液体的黏度.

3 实验结果

实验中选用小球质量m=0.015 95 kg，直径d=0.013 2 m，筒内直径D=0.200 0 m，甘油液面高度H=0.200 0 m.

3.1 测量弹簧振子的平均固有角频率

表1 弹簧振子固有角频率的测量结果

3.2 测量液体黏度

在程序中输入测定的弹簧振子的平均固有角频率、小球质量及直径，将小球作为追踪目标即可开始采集小球的运动轨迹. 调节驱动装置中的频率旋钮，观察实时显示的相对位移-时间图像，判断小球的运动状态. 当小球在竖直方向有最大相对位移时，弹簧振子达到共振状态. 待小球振动稳定后，停止采集，得到如图5所示的弹簧振子的共振图像.

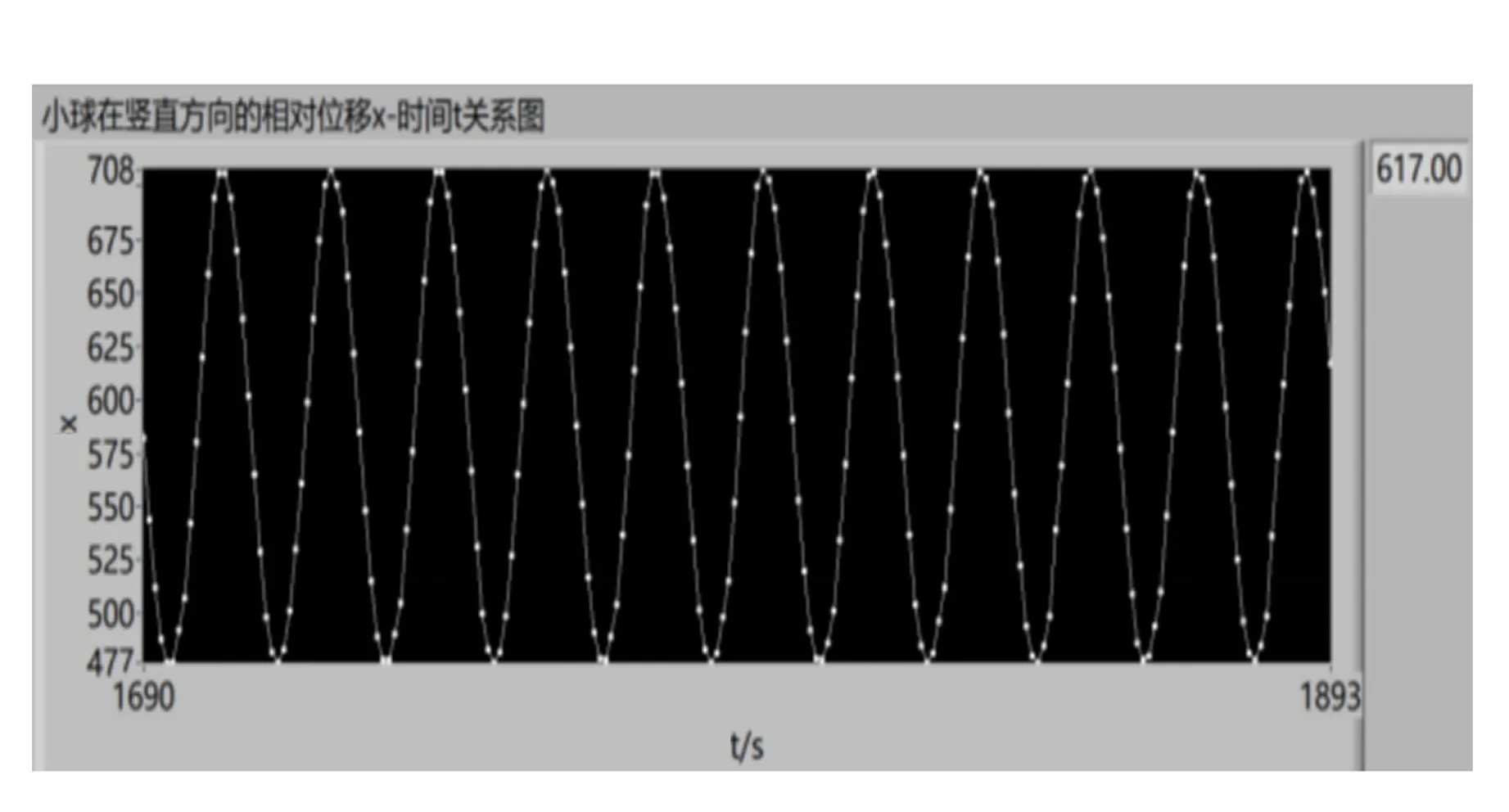
图5 弹簧振子共振图像

获得弹簧振子共振图像后，在测量面板上用区间选择线选定好共振图像中3个振动周期，点击面板“生成结果”键，可以测量出液体的黏度并显示在测量面板上，如图6所示.

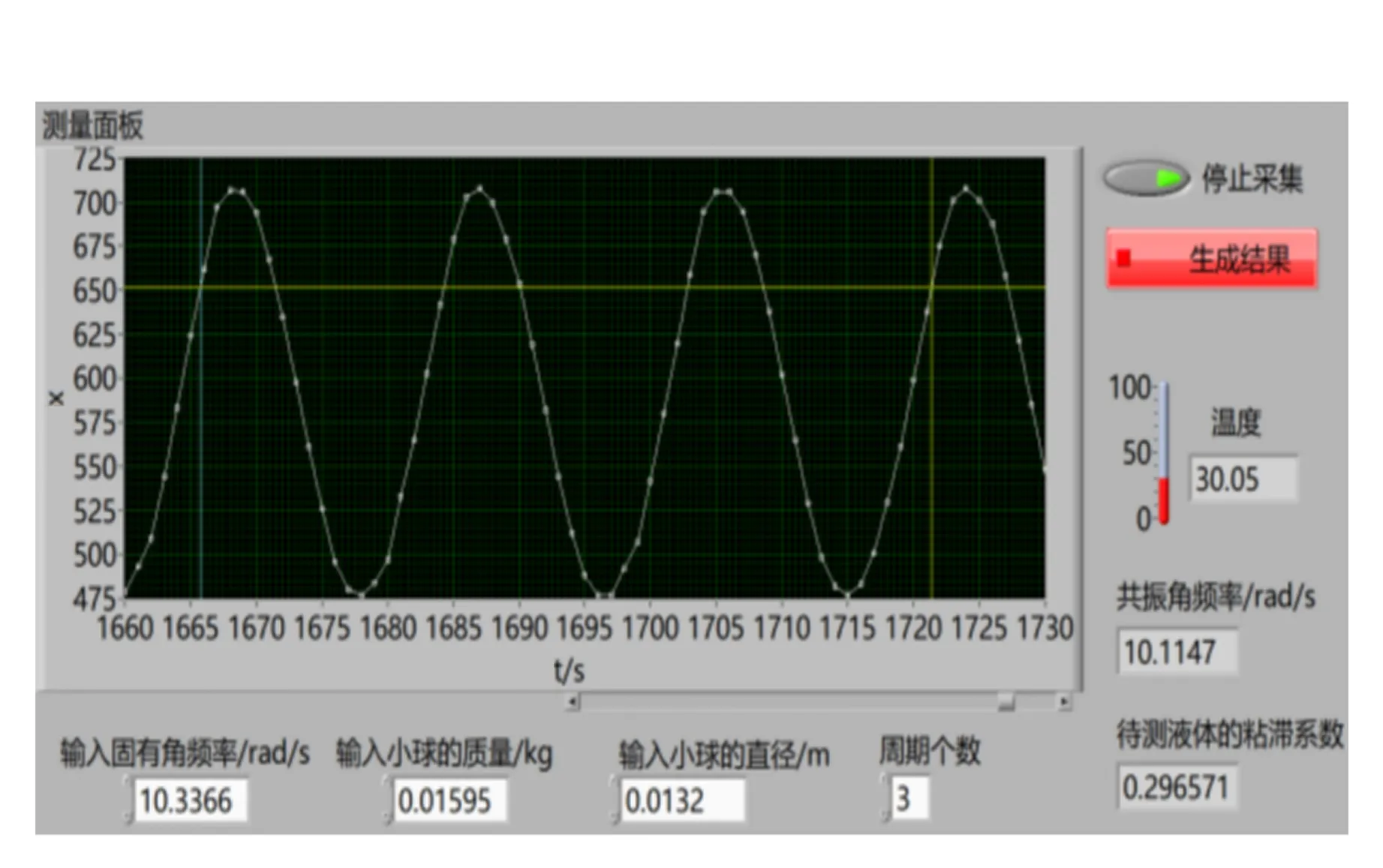
图6 测量结果图

测量温度为30 ℃，质量分数为96.0%的甘油黏度测量结果如表2所示，根据表中数据可得甘油黏度为η=(0.299±0.004) Pa·s，与文献[8]中参考值0.296 7 Pa·s相比较，Er=0.67%,测得的黏度较为准确.

表2 液体黏度测量数据

3.3 测量黏度随温度变化的曲线

利用恒温加热片为甘油加热，重复3.1和3.2中的操作步骤. 测量出不同温度下质量分数为99%的甘油黏度，所测数据如表3所示.

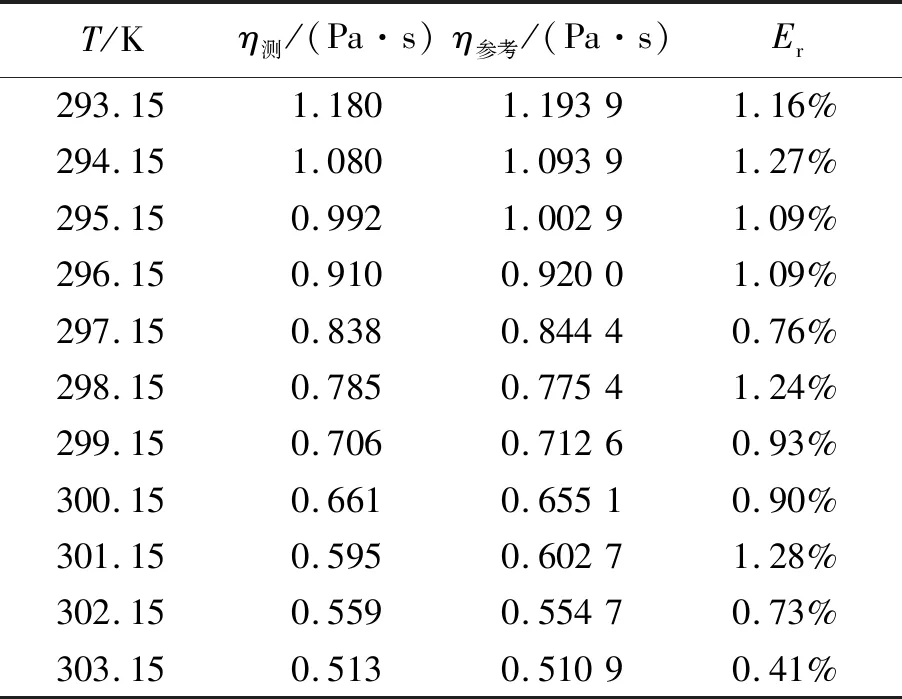
表3 不同温度下液体黏度测量数据

将所测数据与文献[8]中的数据进行比较，其相对偏差均小于2%，说明本文方法的测量较为准确，且可重复性高.

图7为利用Matlab软件拟合的甘油黏度参考值η参考和测量值η测分别随T-1的变化曲线. 2条变化曲线基本一致，均满足指数变化规律[9]. 得出甘油黏度η和温度T的经验公式为

图7 甘油黏度随温度倒数的变化曲线

与参考文献[8]中结论相符.

3.4 测量黏度随质量分数的变化曲线

用蒸馏水稀释甘油，配置出不同质量分数的甘油水溶液，测量出温度22.5 ℃下，质量分数为95%～99.5%甘油水溶液的黏度，测量结果如表4所示.

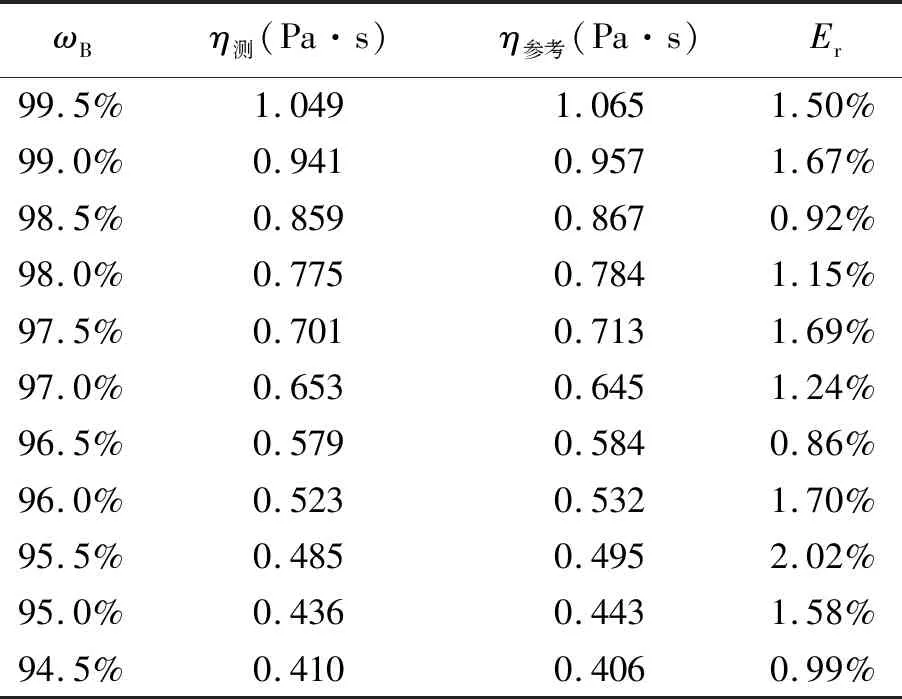
表4 不同质量分数下甘油黏度的测量数据

将所测数据与文献[8]中的数据进行比较，其相对偏差均小于2.1%. 图 8是利用Matlab软件拟合的甘油黏度参考值和实验值分别随质量分数ωB的变化曲线.

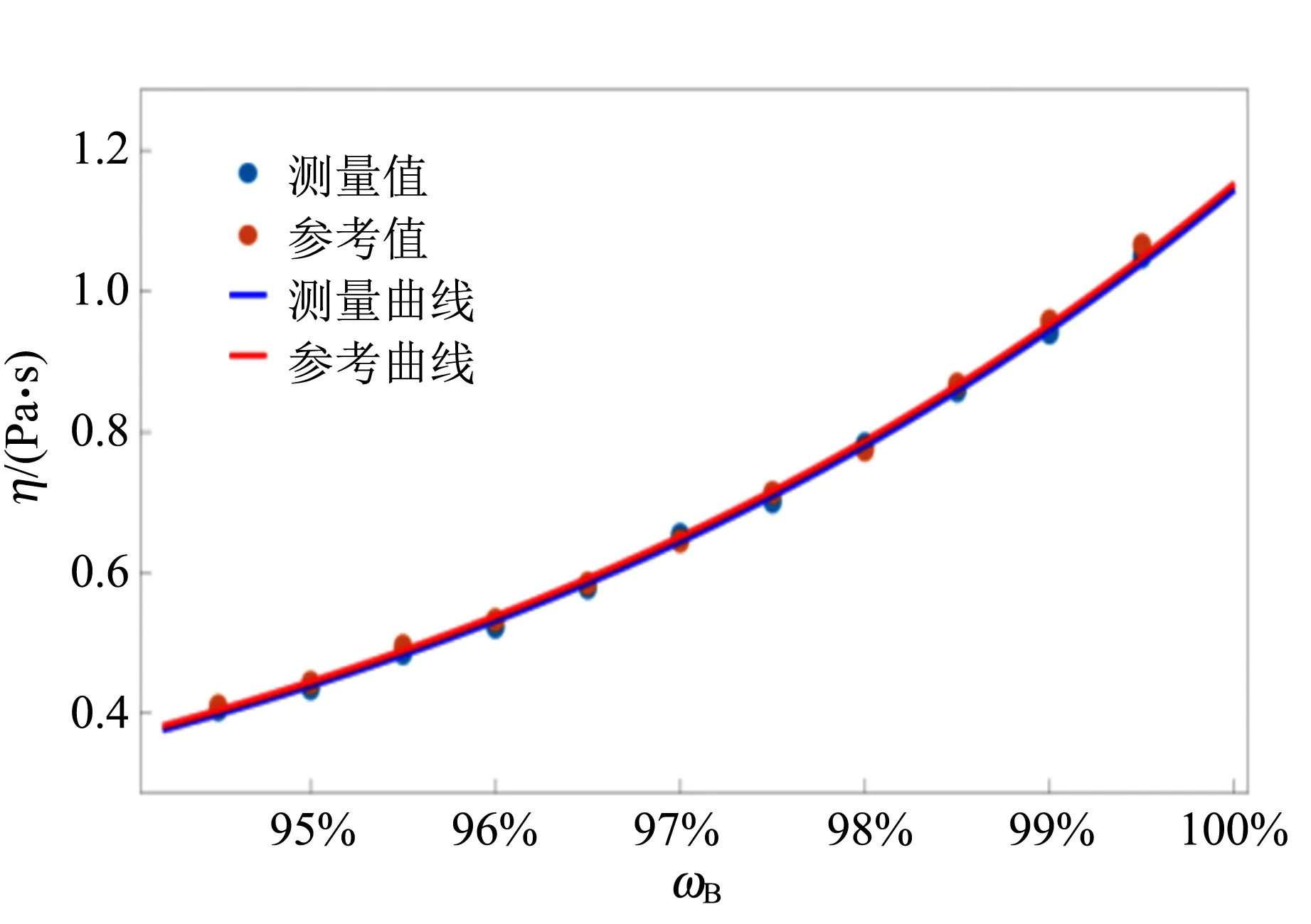
图8 甘油黏度随质量分数的变化曲线

由图8可知实验值和参考值随质量分数ωB的变化趋势基本一致.得出甘油黏度和质量分数ωB的经验公式为

η=5.31×10-9exp (19.199ωB).

由经验公式可知：甘油黏度η与质量分数ωB也满足指数变化规律.

4 结束语

本实验将磁动式扬声器作为驱动源给弹簧振子提供了稳定的周期性驱动力，并且设计了液体黏度测量装置，该装置可一键生成实验数据. 利用该装置测量的甘油黏度随温度、质量分数的变化曲线与参考值基本一致，数据相对偏差都在2.1%以内. 本文所用方法具有操作简单、高效便捷、测量结果精确等特点.