多次散射等过程对卢瑟福散射实验的影响
白 羽,车君彦,王彦博,戴玉蓉
(东南大学 a.物理学院,江苏 南京 211189;b.吴健雄学院,江苏 南京 211102)
在卢瑟福散射中,发生大角度散射的α粒子会和靶中其他原子发生多次小角度散射,导致出射α粒子角分布与卢瑟福散射微分截面所描述的角分布有所偏离. 在实验中对多次散射过程的处理会面临如下困难:a.多次散射过程中主要过程的散射角很小,而小角度散射无法完全由卢瑟福散射微分截面来描述. 一方面,当散射角趋于0时,不能仅考虑原子核与入射粒子间的库仑力,还需要考虑核外电子的屏蔽效应[1];另一方面,卢瑟福散射微分截面描述的是α粒子与单个原子核的散射,当散射角趋于0时该截面模型并不适用[2-5]. b.入射粒子的准直性、靶厚度的不均匀性以及靶、放射源和探测器的空间位置和几何尺寸[6]也会对实验结果带来影响.
实验中,小角度散射数据反映了多次散射过程的角分布,因此在处理实验数据时,可以采用小角度散射数据与卢瑟福散射模型相结合的方法来描述实验数据. 这种方法的优点是可以直接通过小角度数据来分析多次散射、入射粒子准直性等因素造成的影响,而不依赖于卢瑟福散射小角度极限下的理论模型,也不依赖于实验中难以确定的其他因素,例如入射粒子准直性、靶孔边缘散射等先验信息.
1 卢瑟福散射过程与多次散射过程
卢瑟福散射实验通过测量α粒子与重原子核(Au和Pb等)大角度散射的微分截面,揭示了原子具有核的结构,即原子的正电荷与大部分质量集中在原子尺度约万分之一的区域内. 通过对经典的静电力场散射过程的推导,可以证明散射微分截面为[7]
(1)
其中,ε0为真空介电常量,Ek为入射α粒子的动能,Z1e和Z2e分别为α粒子(Z1=2)与靶原子核(金箔Z2=79)的电荷,θ为α粒子的散射偏转角.
然而在实验测量过程中,α粒子除了发生卢瑟福模型描述的散射之外,还可能在金箔中发生多次小角度散射或与靶孔边缘发生散射. 这些过程与卢瑟福模型的散射过程先后发生,对散射微分截面测量造成影响. 多次散射的影响如图1所示. 假设α粒子与金箔中某一层的Au原子发生大角度散射,散射偏转角为ψ2. 而在这次散射发生前,这个α粒子可能已经通过多次小角度散射,与原有的飞行方向发生了一定的偏离,偏转角为ψ1;而在发生散射后,α粒子也可能因为多次小角度散射,飞行方向发生进一步偏离,偏转角为ψ3.
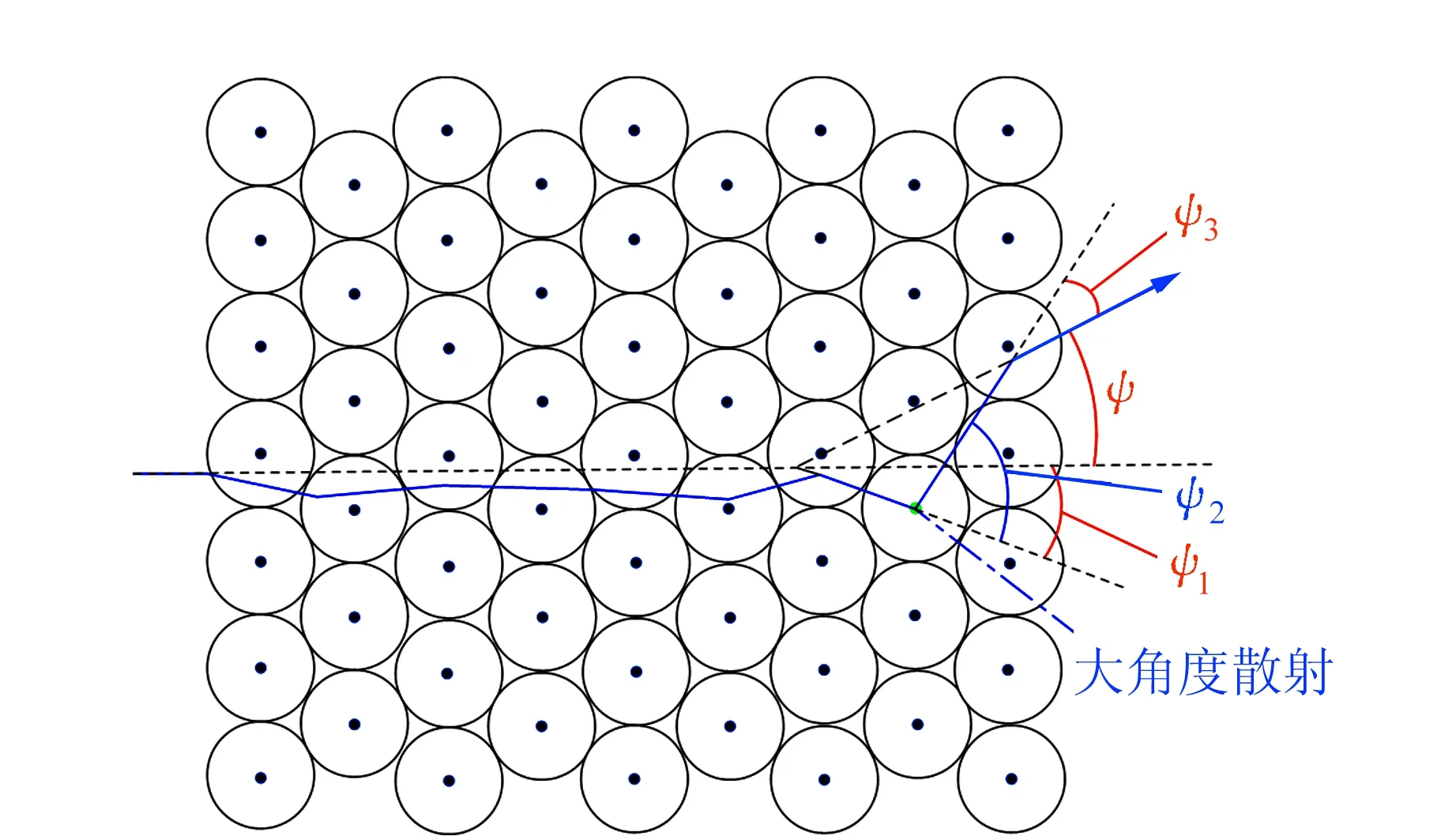
图1 α粒子穿透金箔示意图
因此,α粒子穿过金箔整个过程的效果是在发生1次大角度散射的基础上,通过多次散射过程使粒子飞行方向进一步发生偏转,从而使出射α粒子的角分布发生弥散. 在实验数据中,不能简单地用总偏转角ψ来代替大角度偏转角ψ2. 如何理解和处理小角度偏转造成的影响,是本文要讨论的主要内容.
2 实验装置与测量简介
散射与粒子探测装置被封装在圆柱形金属腔内,如图2所示.

图2 卢瑟福散射装置示意图
该装置包括圆形旋转靶台与Si-Au面垒半导体探测器. 旋转靶台可在步进电机带动下进行旋转. 靶台中间,放射源腔室和靶槽位置沿靶台直径分布. 放射源为Am-241,活度为2 mCi,衰变时发射出动能约为5.486 MeV的α粒子. 靶槽位于靶台中心位置,在实验中,α粒子与靶片(放置于靶槽位置)上的金箔发生散射,经过散射的α粒子可被Si-Au面垒型探测器(已经调节好角度)探测到. α粒子在探测器中产生的信号经过前置放大器放大和数据采集系统的数字化后,被多道读出系统记录. 靶片由2.0 cm×2.5 cm的长方形硬纸板做成,其长度与靶槽宽度一致. 靶片中间开有圆形靶孔,孔中附有厚度为1.22 μm的金箔. 在α粒子的入射面,孔的直径约为5 mm,可以起到准直的作用;在α粒子的出射面,孔的直径为8 mm,如图3所示.

图3 靶片照片
当散射角为θ的α粒子指向探测器中心时,若只考虑单次大角度散射,并忽略散射角在探测器探测单元内的变化,探测器探测到的α粒子计数率期望值为
(2)
其中,n为单位体积内的Au原子数,约为5.91×1022cm-3;d为金箔厚度;I为单位时间内入射到金箔上的α粒子数;η为探测器的探测效率;ΔΩ为探测器探测单元对靶中心的立体角(ΔΩ≪4π).将式(1)代入式(2),可得
(3)
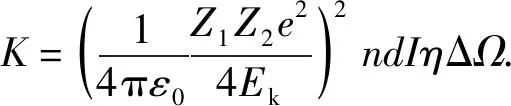
实验使用CAKE1024软件进行控制和数据采集. CAKE1024集成了前端电子学控制、多道读出系统、数据采集控制和记录、步进电机控制等功能. 实验过程基本遵从文献[8]中的步骤,但在以下2方面做了改进:
1)通过拟合小角度散射数据确定0°角的位置,而不是通过调整步进电机来寻找计数率最高处对应的角度,结果更加准确.
2)根据对空靶测量的数据,发现在θ<56°时,本底的计数率远远低于实靶实验的计数率,因此忽略θ<56°时本底计数率;而当θ>56°时,本底计数率显著升高. 补充材料对这个问题进行了介绍,并通过信号事例与本底事例能谱的显著差别对二者进行区分,补充材料二维码如图4所示.

图4 补充材料二维码
3 多次散射过程的统计性质及其影响
1940年,E. J. Willimas使用卷积研究带电粒子在物质中的多次散射过程[9]. 文献[10]对多次散射理论做了全面的综述,通过几何方法对非相干多次散射过程角分布函数进行了推导,得到多次散射的角分布函数的傅里叶变换函数为单次小角度散射角分布函数傅里叶变换函数的乘积. 而根据傅里叶变换的性质,多次散射的角分布函数就是单次散射的角分布函数的卷积. 文献[11]中提出多次散射直接以单次散射卷积为出发点. 本文以该思想为基础,描述采用卷积表示多次散射与单次散射角分布的联系.
沿z轴方向(cosθ=0,并记此方向为Ω0)飞行的准直α粒子束在穿过1层Au原子时发生的散射角分布概率密度函数为
(4)
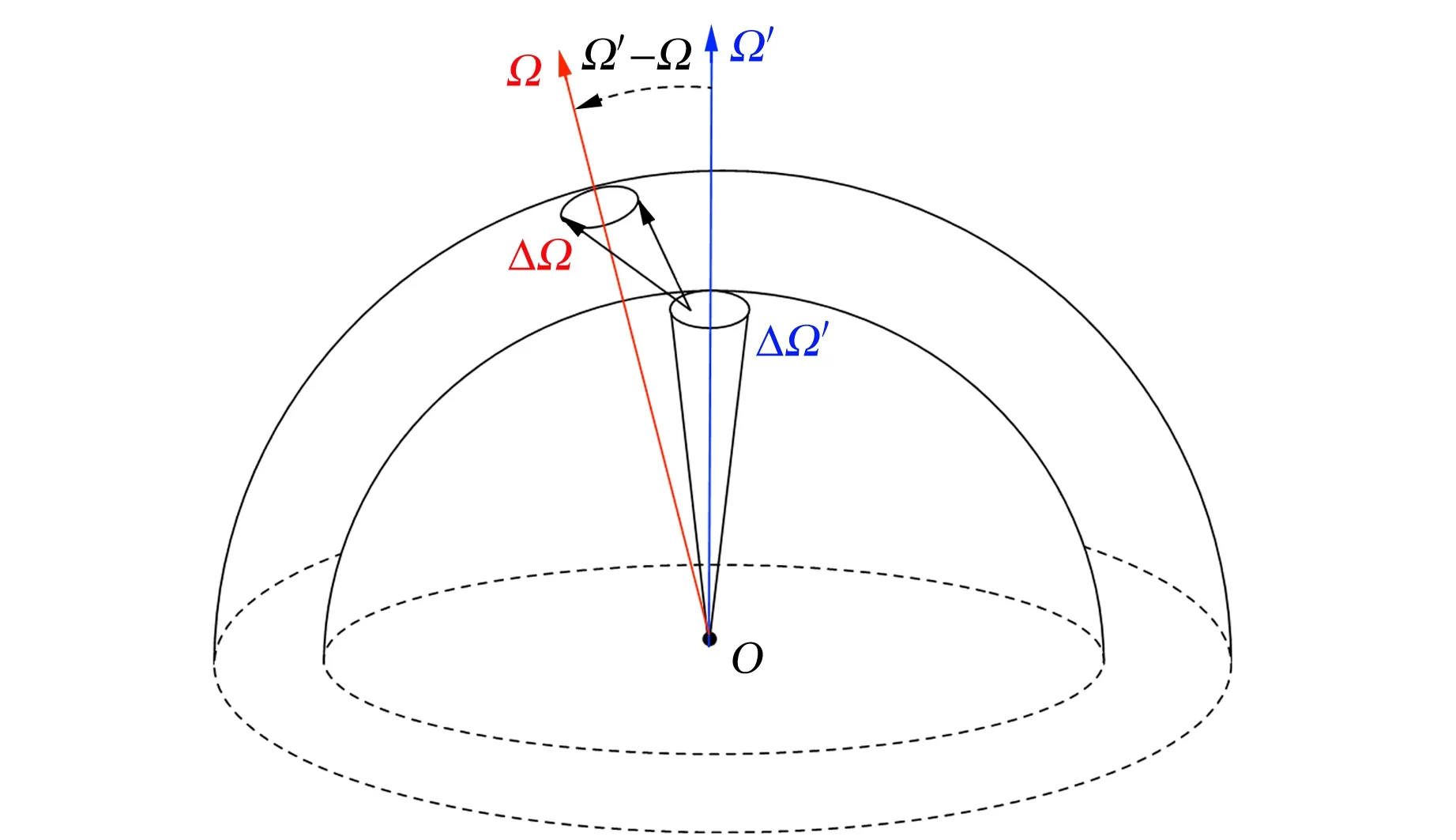
图5 连续散射过程示意图
这是球面上的卷积,可以被记为
F(2)=F(1)⊗F(1).
以此类推,如果粒子穿过N层Au原子,总散射截面可以记为N-1次单次散射微分截面的卷积
该角分布在总散射角足够小时近似服从高斯分布.在角度足够大时,可以认为α粒子至少发生了1次大角度散射,其微分截面由式(1)描述;除了大角度散射外,在穿透金箔过程中,α粒子还与N-1层Au原子发生散射.因此大角度散射微分截面近似地表示为式(1)与N-1层散射截面的卷积,即
(5)
F(N-1)(Ω)和F(N)(Ω)在小角度处非常接近.另外,可以认为只有观测点附近的立体角微元对观测结果有贡献.因此,式(5)中的F(N-1)(Ω)可以近似表示为F(N)(Ω)在小角度的分布,即
(6)
式(6)中卷积并非对全立体角进行积分,而是只限于Ω附近的立体角范围.如果考虑到入射粒子准直性、靶孔边缘的散射和金箔厚度的不均匀性等因素,式(5)中小角度的散射角分布并不能完全由高斯分布描述,但是式(6)仍然近似成立.而此时式(6)中的F(N)(Ω|θ→0)不仅包括由于多次散射造成偏转的效果,还包含了由于入射粒子准直性和靶孔边缘散射等效应造成的偏转角大小.
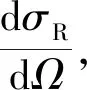
式(5)是球面上的二维卷积,可化简为一维卷积,表示为
(7)
其中,Δθ表示对观测点有贡献的范围.在实验数据处理中,还可以进一步将式(7)中的积分近似由求和代替,即
(8)
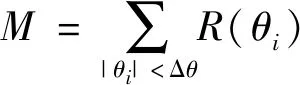
(9)
(10)
上述结论可以通过蒙特卡洛模拟测试(Toy Monte-Carlo Test)来验证. 在测试中,模拟2类物理过程:一类是单次散射过程,服从散射角分布[式(1)];另一类是多次散射过程,服从高斯分布[式(3)],该分布的σθ=5.48°. 因为式(1)有一定的适用范围,在ψ2=10°处对单次散射最小偏转角做了截断. 对大角度散射的观测中(要求偏转角不小于30°),单次散射ψ2<10°的贡献很小. 在补充材料中对模拟的细节做了更详细的说明. 对每个α粒子,如果在散射后的飞行方向在探测器的接受度内时,就记录下1个事例. 首先模拟了160亿个先后发生单次散射和多次散射的α粒子的事例,并模拟对θ=30°~70°之间的事例进行的探测;另外,还模拟了2亿个只发生小角度散射的α粒子,并模拟了对偏转角在θ=-15°~15°之间的事例进行的探测,如图6所示.
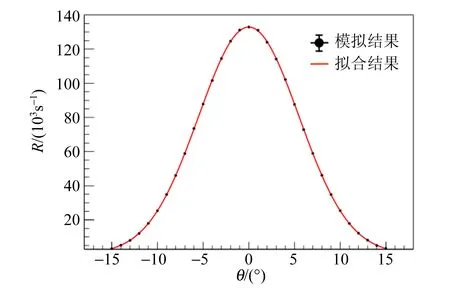
图6 模拟得到的小角度散射事例率分布
使用小角度散射模拟数据分布作为式(8)中的F(N-1)(θ-ψ2)(其中|θ-ψ2|<Δθ=15°).由此,将式(8)计算的结果和模拟结果相比较,发现二者基本一致.如图7所示,模型以及模拟结果都按照计数率最高的点(θ=30°)进行了归一化处理.结果证实了式(8)可以用来修正因为多次散射对卢瑟福散射的微分截面角分布造成的影响.
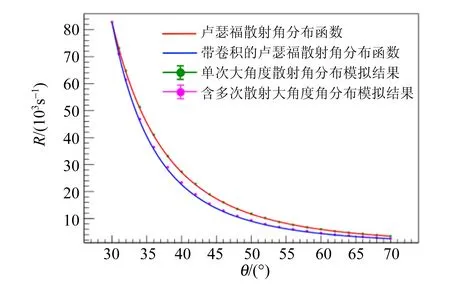
图7 模拟结果与模型的比较
4 实验结果与模型比较
将角分布[式(6)]用于实验数据处理中,从θ=-30°~70°的范围内进行取数. 其中在θ=-30°~31°的范围内,每隔1°取1个数据点;在θ=32°~70°范围内,每隔2°取1个数据点. 为了保证统计量足够多,在大角度取数时,适当延长取数时间. 因为仪器连续工作时间的限制,取数过程分5批次完成. 在每次取数开始时,会重复上一次取数结束时的角度测量. 在θ>50°时,会有从靶边缘之外直接射入探测器的本底过程. 补充材料中描述了对此类本底的扣除方法. 图8所示为测量到的计数率随角度的分布(不同颜色代表不同批次的数据),可以看出,在小散射角区域,散射截面呈现类似高斯分布的形状;而在大散射角区域,数据分布明显偏离高斯分布. 该结果与预期一致.
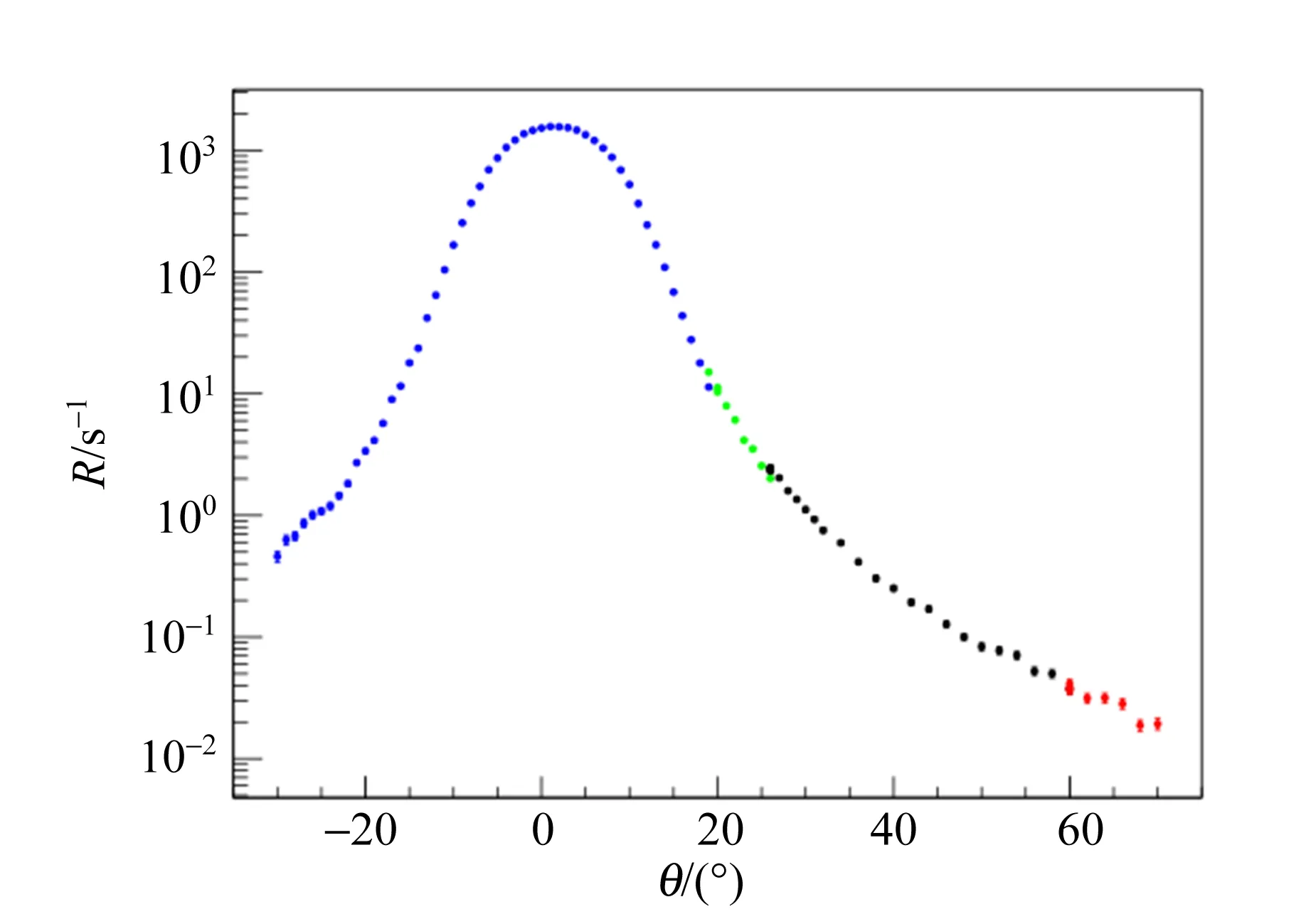
图8 实验数据
对θ=-15°~18°的区域使用高斯分布拟合,如图9所示. 在靠近0°的区域,实验数据与高斯分布有明显偏离,这是因为在这个区域角分布除了受α粒子与金箔散射的影响,还受入射α粒子方向的准直性影响.
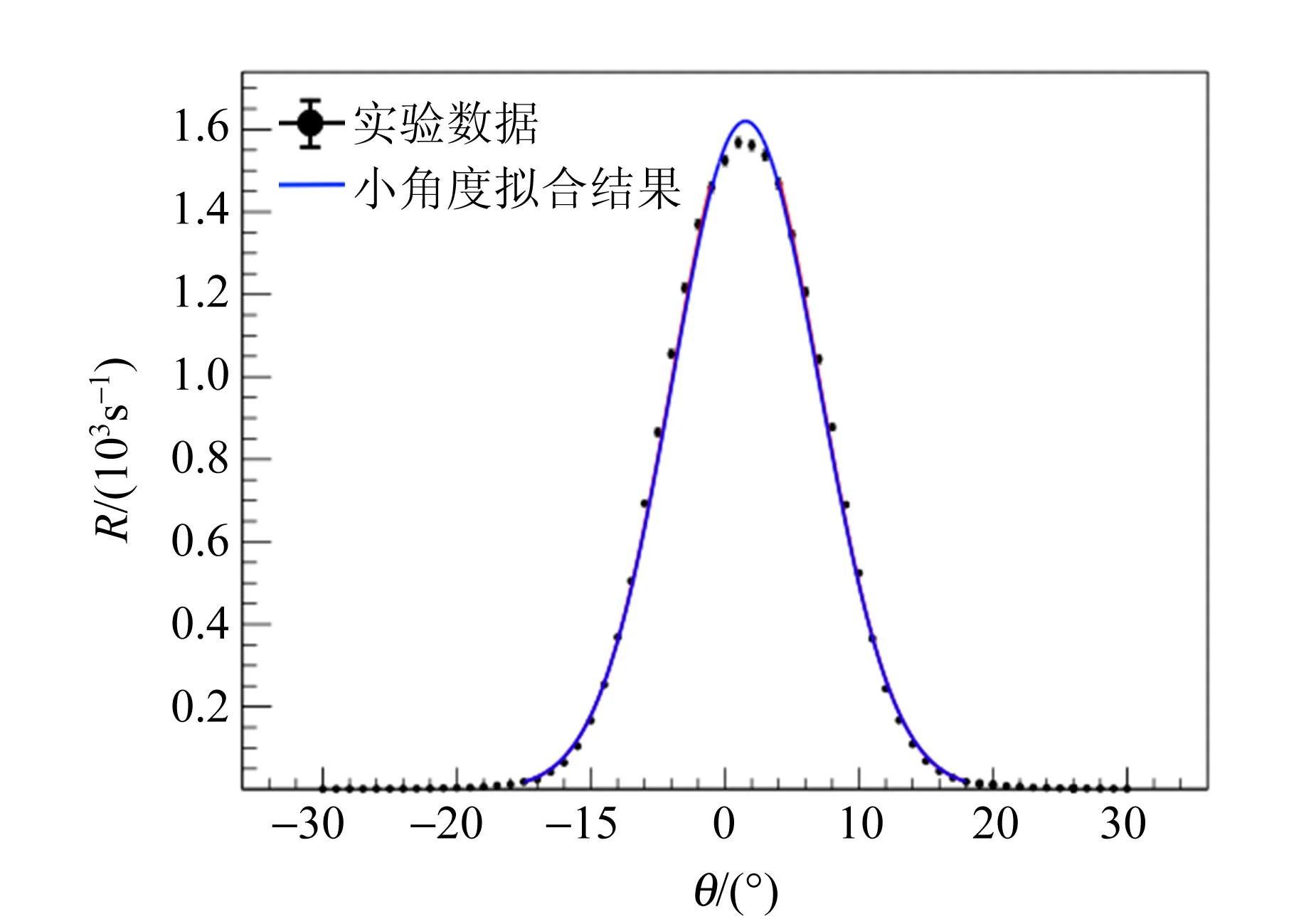
图9 使用高斯分布拟合不同角度下小角度散射数据计数率

在数据中选取偏转角为θ=30°~70°的数据进行研究,认为该范围内探测到的事例至少发生了1次大角度散射,并取式(7)中的Δθ=15°. 在图10所示的大角度散射数据中(模型按计数率最高的数据点进行了归一化),实验数据随角度的下降速度比卢瑟福散射公式预言的速度更快;而通过小角度数据与卢瑟福散射截面卷积的模型则与数据更加符合.
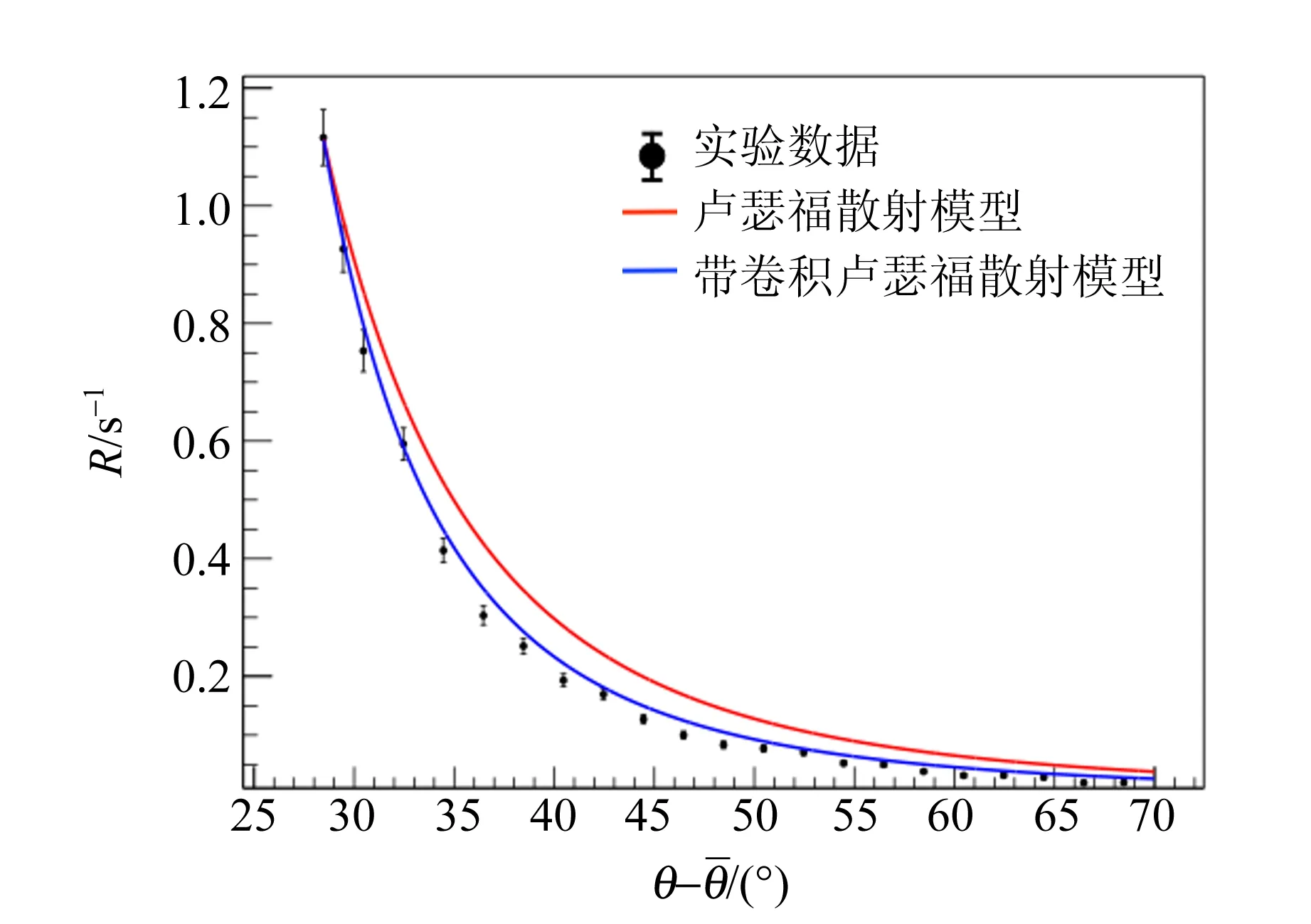
图10 不同角度的大角度散射计数率与模型比较
也可以使用不同的模型对实验数据进行拟合,拟合结果如图11所示.
5 实验结果讨论
对可能影响实验结果的因素做进一步分析和讨论.
5.1 大角度散射造成的穿透距离的变化
在前面的讨论中,假设了α粒子多次散射与大角度散射无关,该假设并不完全准确. 在实际情况中,如果粒子在穿透金箔过程中较早发生大角度散射,那么其将在金箔中飞行更远的距离,如图12所示. 飞行更远的距离意味着粒子会穿透更多层Au原子,因此大角度的多次散射效应较之小角度的情况会更加显著.
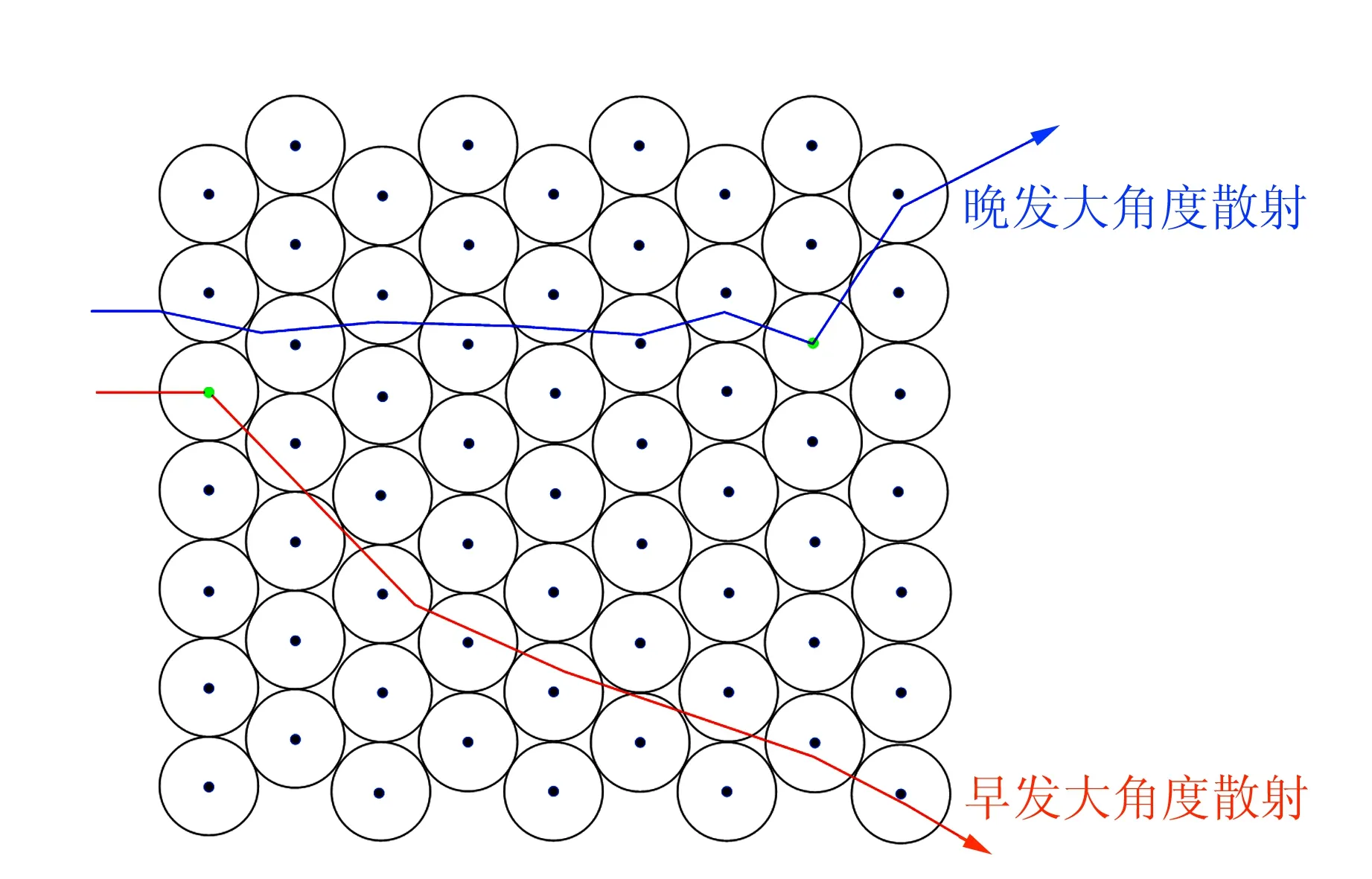
图12 不同位置发生大角度散射示意图
为了研究多次散射与大角度散射之间的相关性,在模拟的基础上,进行不同位置发生大角度散射的探究.具体步骤为:1)先随机模拟出发生大角度散射的位置;2)在大角度散射发生前,根据粒子穿透的距离模拟多次散射;3)在多次散射的基础上模拟大角度散射;4)根据粒子飞出金箔的距离模拟多次散射.
按照实验结果设置模拟参量,以便和实验结果进行直接比较,最终的模拟结果如图13所示(模型及模拟都根据计数率最高的数据点进行归一).从模拟结果可知,考虑了大角度散射穿透距离变化的模拟结果与没有考虑该因素的模拟结果的角分布十分接近.
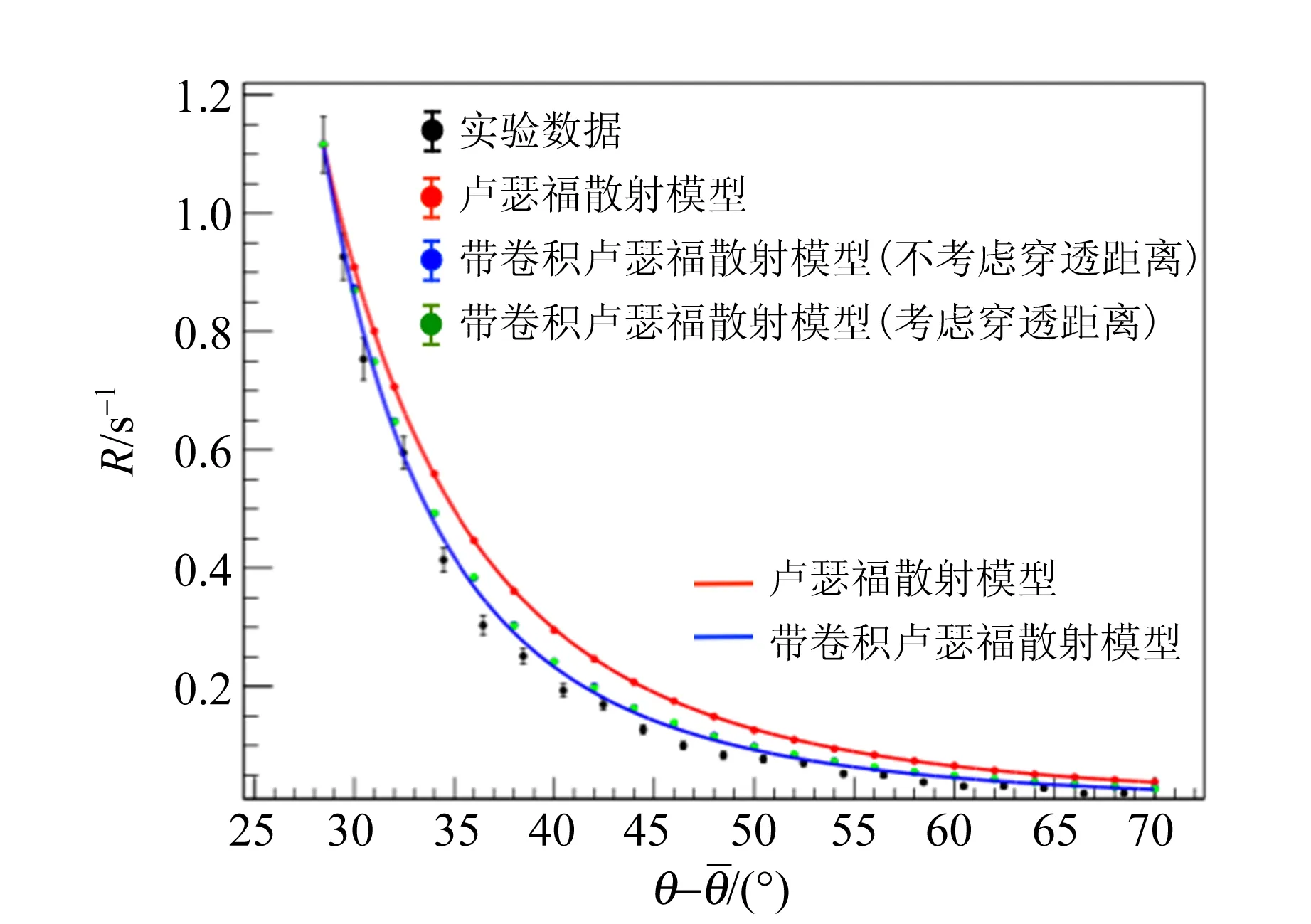
图13 不同模型的大角度散射数据计数率对比
5.2 电离能损及探测效率的影响
当α粒子通过靶时,除了与原子核发生散射,也可以与核外电子发生散射,这样的散射使α粒子动能降低. 根据卢瑟福散射微分截面公式[式(1)],动能降低会导致散射截面变大,从而使得α粒子更容易发生散射. 对大角度散射而言,根据式(1),动能的改变并不会改变散射α粒子角分布函数;而对小角度散射而言,更大的散射截面意味着式(4)中的λ更大,因此相对于无电离能损的情况,α粒子在通过相同厚度的金箔发生更多次小角度散射,这会导致更大的角分布弥散. 另外,电离能损也会导致探测器探测效率的降低. 从数据中可以看到,实验数据随角度变化的趋势仍然快于考虑多次散射效应的模型,探测效率随散射角的变化可能是影响因素之一.
5.3 散射角度的误差
在图8中,同样角度、但不同批次的数据存在显著差异,例如θ=19°时第1与第2批次数据(分别为蓝色与绿色数据点)存在差异,θ=26°时第2与第3批次数据(分别为绿线与黑色数据点)存在差异,这种差异可能来源于步进电机指向角度的误差. 从图8中可以看到,第2批次θ=19°时测得的计数率明显高于第1批次测得的计数率,这表明第2批次数据中散射角θ相较于第1批次数据中的θ偏大. 按同样的道理,在θ=26°时第3批次测到的角度也大于第2批次测到的角度. 如果确实是角度误差导致计数率发生突变,将会导致大角度测量结果中,对实际散射角估计偏大. 而小角度时计数率随角度变化更加迅速,对散射角的高估将会导致计数率随散射角变大而下降的速度更快.
6 结束语
本文研究了多次散射对卢瑟福散射实验的影响. 多次散射会改变出射α粒子的角分布,使得实验结果与理论分析出现一定的偏差. 本文采用卷积来研究多次散射,提出了使用小角度数据角分布与卢瑟福散射模型的卷积来描述大角度实验数据的方法,并通过模拟实验证实了该方法可以较好地描述多次散射的影响. 与卢瑟福散射模型相比,该卷积模型与实验数据符合得更好.

