近邻信号交叉口定向交通管制适宜间距研究*
□ 唐辰晨,盛玉刚
(南京林业大学 汽车与交通工程学院,江苏 南京 210037)
中共中央国务院印发的《关于进一步加强城市规划建设管理工作的若干意见》提到树立“窄马路、密路网”的城市布局理念,其中极为关键的就是如何开发好城市中“小尺度、功能复合”的街区制模式;同时在存量规划时代背景下,老城区通过城市更新等手段促进建成区功能提升。两者不可避免地面临城市信号交叉口因间距过小带来的交通拥堵难题,如上下游交叉口信号配时不合理,导致排队车辆在下游交叉口延伸至上游交叉口物理区,发生死锁现象;驾驶人因强制换道需求,在下游交叉口交织区频繁加减速,不仅导致交织区的交通安全风险增大,还增加了下游交叉口的交通延误。城市路网中现有的近邻交叉口大多处于老城中心,通过拓宽道路等方法进行优化可行性较低。因此,研究如何利用现有的道路资源优化城市近邻交叉口运行状况具有重大意义。
针对城市近邻信号交叉口的优化,现有的研究成果主要集中在渠化、配时、延误、通行能力等方面。从对近邻交叉口间排队车辆进行同步控制策略,提出密集信号控制方案[1];考虑红绿灯设置位置对小间距交叉口的交通影响,综合考虑车辆排放与交通运营提出以200m为间距推荐值[2];将多个信号交叉口理解为共同运动合并到道路固定位置,促使车辆在关键阶段之间循环来降低周期延误[3];提出小间距交叉口不适合采用绿波优化来降低驾驶人超速概率的观点,表明可以通过降低周期长度等方法,在不增加车辆延误的情况下降低驾驶人超速概率[4];利用混合整数线性规划技术,分别确定单点交叉口最优信号配时与信号协调相位差,达到车辆平均延误最小化[5];利用最佳速度量化交叉口容量降低的影响,证明强调模拟信号交叉口时考虑下游影响的重要性并揭示了上游拥堵的原因[6]。国内研究大多在上下游交叉口信号协调上进行优化,考虑不同车流达到随机性、配时合理性等因素建立通行能力概率模型,并进行参数敏感性分析[7];推导小间距交叉口过饱和信号的最大延误模型,并对模型进行了算例分析[8];以小间距交叉口的平均车辆延误作为优化目标,建立了交叉口的协调控制方法[9];通过编写遗传算法程序,建立以车均延误为优化目标的单点交叉口信号配时方案,防止排队车辆溢流至上游交叉口[10];基于双环相位结构,建立信号合并与信号协调对应的信号相序设置与配时方法[11];在保持原有绿波带的情况下,进一步利用模糊神经控制系统协调下游左转与上游直行的交通流[12];提出对于小间距交叉口间的相位差应该以周期为单位进行实时动态调整的观点,建立近邻交叉口相位差优化模型[13]。
以往的研究成果均能在一定程度上缓解交通压力,促进交通有序运行,但是忽略了因近邻信号交叉口所处地理位置的特殊性导致的方案优化中付出的人力、财力,及交通管控造成的不可避免的损失。更为重要的是,下游交叉口交织段因车辆频繁换道而产生的交通安全问题仍然没有得到有效解决。基于以上研究的不足,结合下游交织段拥堵现状,遵循交通负荷均分原则:微观上分离交织段车辆换道冲突,宏观上分化下游交叉口交通压力,达到交通流在空间分布上控密补稀,提出定时定向交通管制交织段的优化方法来加强高峰期下游信号交叉口通行效益,减少交织段内平均车辆延误这一解决思路。综合考虑近邻交叉口饱和流状态下换道安全和上下游交叉口功能区需求长度,建立信号交叉口间距临界值模型。将实际间距低于间距临界值模型的近邻交叉口按比例调整交织段长度进行定时定向交通管制策略仿真,将车辆平均延误作为评价指标,对不同场景下的仿真结果进行对比分析,同时兼顾下游交叉口交织段因车辆换道造成的交通冲突前后次数差异,验证定时定向交通管制策略的可行性。
1 考虑换道安全的最小间距计算模型
针对信号交叉口安全间距的研究,在《城市道路交叉口设计规程》(CJJ152-2010)中规定:各类交叉口最小间距应能满足转向车辆变换车道所需最短长度、满足红灯期车辆最大排队长度,以及满足进出口道总长度的要求,且不宜小于150m。但考虑高峰期下游交叉口交织段复杂的道路环境,该值存在一定的安全隐患。参考交通调查数据、车辆可接受间隙理论、稳定交通流特性、交叉口功能区等来确定交叉口最小间距,对于降低城市主次相交道路交通拥堵程度具有一定积极意义。本文选择从交叉口功能区及车辆安全变道两个因素出发,计算信号交叉口的最小间距临界值,如图1所示。

图1 交叉口间间距组成示意图
1.1 基于驾驶人可接受间隙理论的换道距离
交织段车辆安全行驶距离受本身交通流特性的影响,虽然饱和流和自由流车辆换道时间差别不大,但是两种交通流行驶速度、遇见可接受间隙概率均有差异,所以车辆在交织路段前行距离有所不同。
针对城市近邻交叉口交织段交通流特性,对车头时距的描述可选用连续性分布:负指数分布、移位负指数分布、爱尔朗分布、M3分布等。对于本文研究的高峰期近邻交叉口常处于饱和甚至过饱和状态,普遍采用的负指数分布、移位负指数分布模型适用于交通量小于500pcu具有很大的局限性[14],在信号交叉口下游交织段接近饱和状态时,采用二阶爱尔朗分布能较好地拟合车头时距分布[15]。但将其实际运用于车头时距分布模型中时,会出现部分不合理的较小车头时距,为修正这种情况,将曲线右移一个间隔长度,得到修正后的移位二阶爱尔朗分布曲线。
其车头时距大于等于t的概率为
P(h≥t)=[λ(t-τ)+1]e-λ(t-τ)
(1)
式中:τ为车头时距最小值,考虑高峰期交叉口交通流特性,取值为1s,λ为单位时间到达率,通过交通调查实测取值。
驾驶人在大部分情况下未遇见适宜换道间隙时,会拒绝掉i个不满足换道条件的车辆间隙,其概率为
P(i)={1-[λ(tc-τ)+1]e-λ(tc-τ)}i[λ(tc-τ)+1]e-λ(tc-τ)
(2)
式中:tc为车辆可接受换道间隙,取值为3.5s。
(3)

(4)
(5)
驾驶人在等待时间所行驶的距离为
(6)

驾驶人发现后方出现可接受间隙到换道结束可分为三个阶段:降低车速等待可接受间隙位置与车辆接近平行时间,判断符合可接受间隙位置条件后开始进行换道操作的驾驶人反应时间,换道过程中横向移动时间。国内已有研究成果表明,换道车速约为平均车速的76%。
(7)
式中:Vc为换道车速;ΔV为平均车速与换道车速的车速差;反应时间为确保换道安全取值为2s,n为跨越车道数;横移单车道时间取值为3s。
驾驶人在进行整个换道操作所行驶的长度为
(8)
1.2 上游交叉口功能区长度
驾驶人反应时间行驶的距离、车辆减速的行驶距离、停车排队长度组成上游功能区。一般情况下,驾驶人充分辨识一个动视野目标需要1.0s,感知反应的时间取2.0s。其上游功能区长度公式如式(9)。
(9)

1.3 下游功能区长度
驾驶人在即将穿越交叉口时,仍会在接近交叉口区域受到相交交通的影响,所以下游功能区选择加速车道长和停车视距作为参考指标。而本文所研究的小间距信号交叉口,直行和转向车辆完全分离,因此不考虑加速车道长度。综合考虑高峰期下游交叉口交通流特性与参考《城市道路设计规范》(CJJ37-2012)中针对信号交叉口下游功能区停车视距的要求,下游功能区长度取值为30m。
综上所述,城市道路近邻交叉口的间距临界值模型为
(10)
式中:LM为交叉口间最小间距临界值;LC为下游功能区长度。
以车辆在交织段饱和流状态下的安全换道所需长度为核心所建立的最小间距模型与国内学者以交通流理论、驾驶人生理特性[16]、车队离散理论、信号时段车流运行规律[17]等为研究基础建立的间距模型在城市道路中有较高的重合。
2 下游交叉口交织段定向交通管制适宜间距研究
定向交通管制通过禁止车辆变道来减少车辆交织,达到减少车辆间的横向干扰、提高车辆运行速度的目的,能极大地保证主要车流方向车道的通行能力。目前,国内外对于定向交通管制的应用多见于城市快速路、高架等主要连接干道,暂未有将其运用在城市中心路网的先例。为直观地研究定向交通管制对小间距信号交叉口间所适宜的间距范围,利用VISSIM仿真模拟在改变影响因素条件下控制优化效果的变化。通过SSAM对车辆轨迹进行交通冲突的分析和统计,SPSS建立适宜间距数学模型。
图2 仿真路网示意图
选取图2的近邻信号交叉口为研究对象,保持各个交叉口信号周期、车道数和流量不变,只改变交叉口间距,对同一间距交织段进行定向交通管制优化,取优化前后数据进行对比分析,将车辆平均延误作为交通效益的指标。由于该交叉口间距低于双向四车道(见式10)间距临界值要求,将100m作为间距仿真初始值,25m作为间距间隔值,利用数据检测点对路网车辆数据进行收集。分析整个交叉口间平均延误和到达车辆情况。
在交通仿真过程中,由于软件设置原因,无法直接输出车辆数据来反映交织段交通安全程度变化。因此选用交织段中的交通冲突作为间接手段,从侧面反映定向管制前后交通安全性的变化。将SSAM替代安全评价模型,对冲突参数进行设定,得出整个路网安全评价。
仿真结束后,将数据检测器收集的数据导入SPSS软件,得到表1。
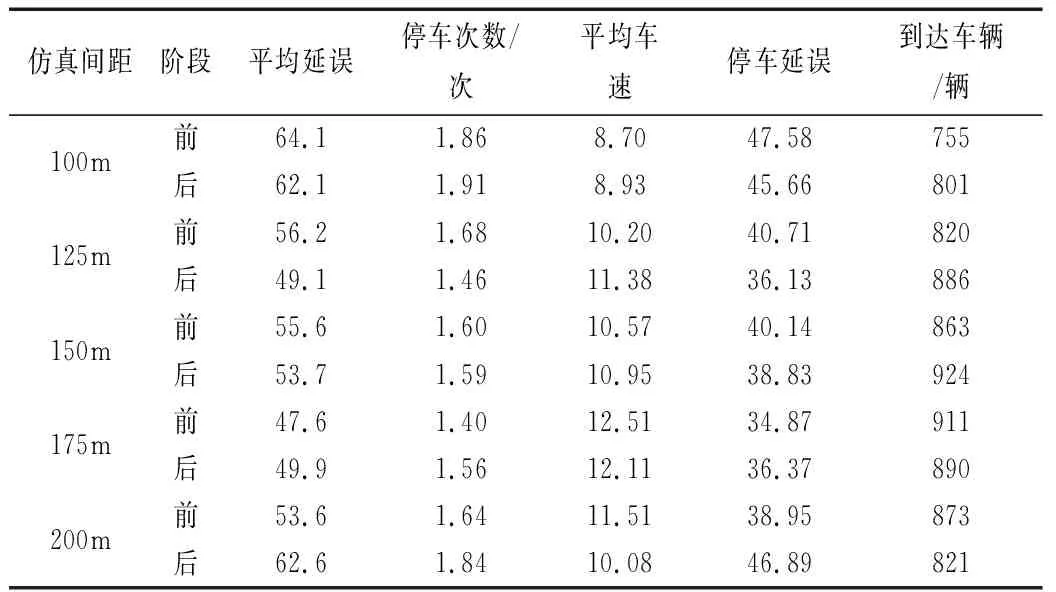
表1 不同间距施行定向交通管制前后数据表
选择平均车辆延误作为评价指标,利用SPSS软件拟合非线性回归方程,通过找到相应的数学模型,确定定向交通管制最适宜的交叉口间距。所得的拟合方程为
y=5.435×10-6x3-0.502x+108.459
(11)
式中:y为不同间距对应的车辆平均延误;x为两交叉口间距。拟合优度R=0.927,R2=0.859,拟合的效果较好。
将式11进行求导分析得出相对应的适宜间距130m的车辆平均延误数据进行前后对比,发现施行定时定向交通管制后,车均延误降低14.4%。将管制前后的车辆轨迹导入SSAM并设定判别车辆距离碰撞时间、后侵占时间等阈值。为提高结果准确性,参考以往研究[18],将距离冲突时间的阈值设置为1.6s,减少由于不合理跟驰模型和变道模型所导致的误差,可以得到优化前后交叉口间冲突次数的变化,以此次数的变化来评价安全程度的变化。冲突次数由优化前的472次减少至183次,降低了61.31%。支路车流进入次干路之后,与其他方向车流相互干扰严重,有明显的换道冲突,不同间距在采用定向交通管制后,交织段换道交通冲突明显减少,绝大部分为追尾冲突。定时定向交通管制针对高峰期近邻交叉口交织段换道冲突有明显优化作用。如图3、图4所示。
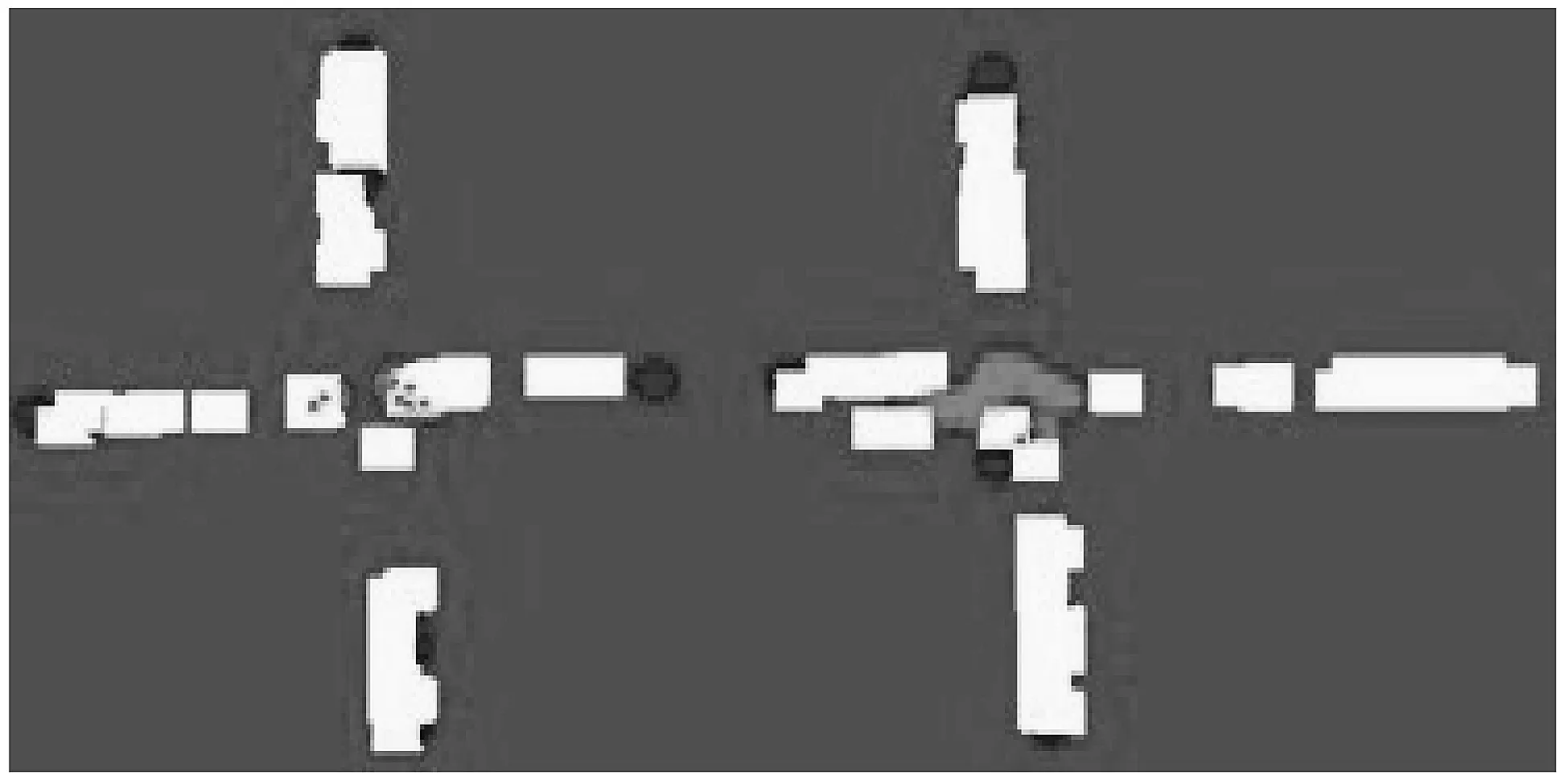
图3 定向管制前交通冲突图

图4 定向管制后交通冲突图
3 结语
针对现有研究对下游交叉口交通安全问题未能得到有效解决这一现象,以近邻信号交叉口交织段换道冲突作为研究重点,提出一种将定时定向交通管制运用到高峰期下游交叉口交织段的优化策略。建立考虑换道安全的间距临界值模型,并通过交通仿真与安全性评价,探究定时定向交通交通管制在不同条件下适宜的交叉口间距。主要结论如下:
①相比于国内外研究成果,定时定向交通管制策略对土地资源并无额外需求,释放下游交叉口通行能力的同时降低了交织区交通安全风险,使得该策略具备广泛运用的前景。
②与传统交叉口间距模型相比,考虑高峰期饱和流状态下换道安全所建立的小间距交叉口间距临界值模型在城市道路的运用更具有一般参考性。
③传统的交叉口交通安全评价大多以统计事故数量为基础,其中较为明显的不足为评价周期长、结果真实性不足。本文以交通冲突数据作为基础,建立以换道冲突为指标的安全评价方法。
④由于研究条件有限,对于定向交通管制的适用性证明只是利用仿真软件进行验证,且只针对单一的道路场景,并未进行实际的应用,实用效果还有待工程检验。

