基于同时送取货多车型二维矩形装箱问题的优化

陈其赛，倪静

基于同时送取货多车型二维矩形装箱问题的优化

陈其赛，倪静

（上海理工大学 管理学院，上海 200093）

研究同时送取货的二维矩形装箱问题，即在考虑客户的送取需求、货物的尺寸和质量，以及多车型约束下求得车辆待装空间最高平均空间利用率。提出含9种适应度值的skyline装箱方案设计改进的混合禁忌搜索–遗传优化算法来求解带同时送取货约束的二维矩形装箱问题。通过仿真检验，混合算法使车辆待装空间平均空间利用率达到88.04%，并求得了服务8位客户的同时送取货装箱方案。基于带9种适应度值skyline装载方案的混合禁忌搜索–遗传优化算法针对同时送取货模式的二维矩形装箱问题能求得较高的空间利用率，并完善了同时送取货模式在装载方面的研究。

二维装箱问题；同时送取货；多车型；skyline；禁忌搜索‒遗传算法

装箱问题是一个在物流行业中经常遇到的经典问题，这类问题需要将货物在配送中心通过合理规划装入配送车车厢中，再运输前往不同的客户点。根据货物的属性不同，在装载过程中往往受到不同的约束，以装载状态为依据可以将装箱问题划分为二维装箱和三维装箱2种类型。二维装箱约束的车辆路径问题（Two-Dimensional Loading Capacitated Vehicle Routing Problem, 2L-CVRP）是二维矩形装箱问题（Two-Dimensional Orthogonal Packing Problem, 2-DOP）和带容量约束的车辆路径问题（Capacitated Vehicle Routing Problem）的联合优化问题，而学者们的研究以VRP为主。装箱问题的优化也可以在物流作业中有效降低物流成本，其中，对于大型企业、零部件供应商等这类客户群体来说，由于标准化作业待送货物均被打包成单层或双层堆叠从高度考虑刚好放入车内的状态。此时货物的装载因素取决于货物底面是否能装入车中，而这一类问题就属于2–DOP。此外，在现代物流中，针对不同的客户群体存在不同的运输模式。对于存在多级加工工厂、供应商的企业或者超市、便利店等这类每日既要进货又有未售罄生鲜需要回收的商户来说，同时送取货这一更贴近实际客户需要的物流配送模式也正逐渐成为广大学者的研究重点，因此，文中以二维矩形装箱问题为核心，针对实际物流环境结合同时送取货配送模式展开研究。

关于装载问题，Wei等[1]针对二维装载问题，提出了改进最佳拟合启发式算法并引入适应度值去选择适合装载的货物，再使用一种时间复杂度为的简单局部随机搜索算法来改进解；同时，Wei等[2]针对长度不限的带卸载约束二维装箱问题，引入了开放空间的概念，提出了一种基于开放空间的首次拟合启发式算法来求解装箱模式，再通过无参数的局部随机搜索算法来改进解；黄子钊等[3]针对实际场景下的自动化码头集装箱堆场出口箱箱位分配问题，开发了一种基于强化学习的超启发式方法来提高堆场作业效率；张长勇等[4]针对航空货运背景下流水线上货物的装箱问题，在考虑一系列现实约束的条件下设计一种拟人启发式与遗传相结合的组合启发式算法，使得货物垛形规划更为紧凑，稳定性更高；张煜等[5]考虑堆场派送顺序，构建了混合目的港贝内排箱问题的整数线性规划模型，利用改进遗传算法求解最小化船舶贝内横倾力矩；那日萨等[6]针对7种现实约束的集装箱三维多箱异构货物装载优化问题，提出了一种基于“块”和“空间”的启发式算法，该算法在时间效率和体积利用率上均优于已有的同类研究；李孙寸等[7]利用多元优化算法实现三维装箱问题的求解说明用多元优化算法实现三维装箱问题的有效性和可行性；吕雪菊等[8]考虑货物的稳定性、定向性以及完全切割约束，通过半径多样化小生境遗传算法对模型进行求解使得车辆空间利用率最大化；Rakotonirainy等[9]研究二维条形装载问题，在给定了1组货物尺寸固定，待装空间宽度固定而高度不限的条件下提出了2种改进的启发式算法，通过4组测试问题根据特征说明算法比现有文献的算法更加优越；Araya等[10]研究单个集装箱装载问题，研究如何使装载货物的集装箱装满总体积最大化，通过提出一个新的评价函数来进行排名从而确定适合装载货物的集装箱，与其他较先进的算法对比能得到更优的结果。

关于同时送取货问题，该研究更贴近于实际，考虑车辆在实际配送任务中不同客户的需求，国内外已有不少学者研究，但对于同时送取货模式的研究更多的倾向于路径中，很少有文献研究配送初期装载阶段。徐小峰等[11]考虑了同时送取货需求带模糊容量限制的动态选址问题，通过改进五角模糊数隶属度函数来表示模糊容量约束，再通过禁忌搜索与自适应大规模领域搜索算法结合的混合算法来求得可行解；王超等[12]首次设计了回溯搜索优化算法来解决带时间窗同时送取货问题并证明有效性；Yong等[13]研究了多配送中心同时送取货的车辆路径问题并利用非支配排序遗传算法求解；周咏等[14]研究冷链物流同时送取货车辆路径优化问题；谭巍等[15]研究车辆负载量的不断变化情况下引入候选集合的策略,将启发因子设为目标函数值并利用蚁群系统与2-opt结合的启发式算法求解模型；Atefeh等[16]考虑到供应链管理中残缺产品库存的不确定性，通过适用于等式约束的鲁棒优化方法以及改进模拟退火算法、遗传算法求解模型，并分析算法性能。

关于装载路径问题，李彤等[17]考虑在不确定需求环境下，针对循环取货问题提出基于VRP与3D–KLP协同优化模型并且设计了求解该模型的多阶段算法；颜瑞等[18]研究包含时间窗、多车场因素的二维装箱车辆路径问题并提出了由量子粒子群算法和引导式局部搜索算法组成的混合算法求解该问题；尚正阳等[19]考虑LIFO装载约束设计了最少剩余开放空间的货物装载方法并开发了带有回火过程模拟退火操作的ISA–LOS算法求解问题；李珍萍等[20]考虑互斥产品的装卸顺序、运输时间等约束设计改进遗传算法求解模型；Wei等[21]针对2L–CVRP问题利用变邻域搜索算法进行求解并且对skyline启发式算法进行改进以适应检查装载约束；Wei等[22]还针对2L–CVRP问题设计了一种具有反复冷却和回火机制的模拟退火算法，采用基于开放空间的启发式算法求解装载方案；Corinna等[23]在考虑车辆装载路径问题中的轴重问题时车辆货位进行详细的二维或三维规划，采用外层为解决路径问题的自适应大邻域搜索算法内层为解决装载问题的最深–底层–左填充算法组合的混合算法求解；Côté等[24]研究二维装载路径问题，提出针对路径的多类子问题量化直接解决此类复杂问题而不是以非综合方式解决单个问题可带来的潜在效益。

综上所述，专家学者们在现有文献中，针对同时送取货模式的研究更多倾向于配送路径阶段，但是装载加路径才形成整个物流配送，而对于装载阶段的同时送取货模式研究较少。基于同时送取货的二维矩形装箱是实现同时送取货配送模式的基础，建立一个求解同时送取货配送模式的空间利用率数学模型，选择高效合适的装箱策略有助于提高车辆的空间利用率，减少车辆的使用降低成本，具有研究意义。依据实际情况，物流企业往往会准备多种车型的车辆根据货物的数量大小进行选择匹配，这是节约成本的一个直接有效的方法。文中在以上研究基础上，综合考虑客户同时送取货需求、多车型车辆以及二维装箱约束等因素，建立了基于同时送取货的多车型二维矩形装箱问题模型（Two-Dimensional Orthogonal Packing Problem with Simultaneous Delivery-Pickup，2–DOPSPD），引入带适应度值的skyline装箱策略寻找装箱方案并设计改进禁忌搜索–遗传混合算法求解该问题。首先对研究问题进行问题描述并建立其相应模型。其次提出设定适应度值的skyline方法寻找装箱方案，设计禁忌搜索–遗传混合算法并介绍相关优化策略。接着通过随机生成不同规模大小的算例与其他启发式算法进行对比仿真实验，再针对非同时送取货模式装载算例进行仿真求解验证算法的稳定性与实用性。最后证明文中所提出的模型和算法解决同时送取货问题的可行性以及对未来的展望。

1 模型建立

1.1 问题描述

文中构建了基于同时送取货的多车型二维矩形装箱模型，具体问题描述如下：存在一个容量不限的配送中心，该配送中心服务多名客户，客户既有送货需求也可能存在取货需求且需求的货物数量、重量和尺寸均已知，每位客户均只能接受一辆物流配送车的服务。配送中心存在多种尺寸不同的车型，根据服务客户的需求选择适宜的车辆进行服务，每种车型的可装载空间尺寸也均已知，可将该空间看成一个矩形。客户的所有货物均可看成长宽已知的矩形，车辆在服务过程中客户所有的货物均需能被装入车中且满足容量、重量约束，货物在装载过程中其中一边必须与车辆的边呈正交或者平行，货物之间不可重叠，在任何服务点客户待取货物也需装入车内且满足装载约束，若无可行装箱方案则需采用更大尺寸的车型。

1.2 符号与决策变量

为了更好地描述2–DOPSPD的数学模型，对文中使用的符号说明如下。

为空间利用率；为客户总数，当时表示配送中心；分别为客户的待送、待取货物总数；为车辆种类数；为客户第件待送货物的长宽；为客户第件待取货物的长宽；为第种车装载区域的长宽；为客户第件待送货物的占地面积；为客户第件待取货物的占地面积；表示第种车的最大可装载面积；表示客户第件待送货物的质量；表示客户第件待取货物的质量；表示第种车的最大载质量。为决策变量，分别表示当客户的第件待送货物、第件待取货物由第种车服务时则为1。

为了更直观的表达出货物在车中的放置情况，建立一个笛卡尔直角坐标系。坐标系的坐标轴分别对应车厢的长宽，坐标系的原点对应车厢左上角。货物的左后下角位置用坐标表示，货物的右前上角位置用坐标表示，则有。表示客户第件装入车辆的待送货物左后下角点的坐标；表示客户第件装入车辆的待取货物左后下角点的坐标。

1.3 模型

基于以上的参数定义以及之前的假设条件，本文在此建立如下数学模型：

(1)

(2)

(3)

(4)

(5)

(6)

(7)

其中，目标函数(1)表示最大空间利用率。约束(2)表示车辆上装载的货物总面积不会超出车厢最大可装载面积。约束(3)表示车辆上装载的货物总重量不会超出车辆最大载重。约束(4)表示货物不能超过车厢可装载区域边界。约束(5)表示货物两两之间不能相交。约束(6)表示货物需要和车厢平行或者正交。约束(7)定义决策变量是0—1变量。

2 算法设计

2.1 基于skyline的装箱方案设计

求解2–DOPSPD问题的关键在于如何涉及一个高效合理的装箱方案，文中的GA–TS算法根据Bottom–Left Fill(BLF)原则见图1，在skyline中选择最左下角的线段作为放置货物的候选区域。在图1a中点3所在的线段为装载区域中最低位置，从待装载的货物中选择合适的货物放入该位置，若存在多个适合放入的货物则利用适应度评价函数选择最适合的货物，放入后形成新的装载区域如图1b所示。若此时剩余待装货物中没有一个货物能放入图1b中点3所在区域，即所有待装货物的宽度均大于，则将点3所在区域视为浪费空间，将该线段提升至相邻最低线段的高度并更新skyline，如图1c所示，浪费空间将不会在后续中继续使用。

2.2 适应度取值规则

2.3 禁忌搜索–遗传混合算法构建

2–DOP是以装载率最大为目标的装载问题，显然该类问题属于经典的NP难问题，遗传算法、蚁群算法等元启发式算法已被证明能很好的解决此类问题，其中，遗传算法是一种通过模拟自然进化过程搜索最优解的方法，该算法通过数学的方式,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程，可以较快的获得较好的优化结果，但是当求解规模或复杂度增大时该算法对新空间的探索能力有限，容易早熟，结果会收敛至局部最优解。由于同时送取货约束、载重约束、装载约束以及多车辆等多重约束的制约致使2–DOPSPD问题在使用遗传算法求解过程中难以跳出局部较优解，算法性能因约束较复杂而受限。为此，文中参考了文献[9]中将禁忌搜索与自适应大规模领域搜索算法相结合的方法，将禁忌搜索算法与遗传算法结合，有助于算法在求解过程中增大对非更优解的接受能力，跳出局部寻优求得更优解。禁忌搜索算法作为一种亚启发式随机搜索算法，它从一个初始解出发，选择一系列的特定搜索方向作为试探，通过建立禁忌表选择实现让特定的目标函数值变化最多的移动。通过特赦准则建立禁忌表可以有效帮助算法跳出局部，增加全局搜索能力这恰好能解决遗传算法中容易陷入局部寻优的不足问题。综上所述，文中通过结合2种算法的优点设计该禁忌搜索–遗传算法来解决该问题，整体流程图见图3。

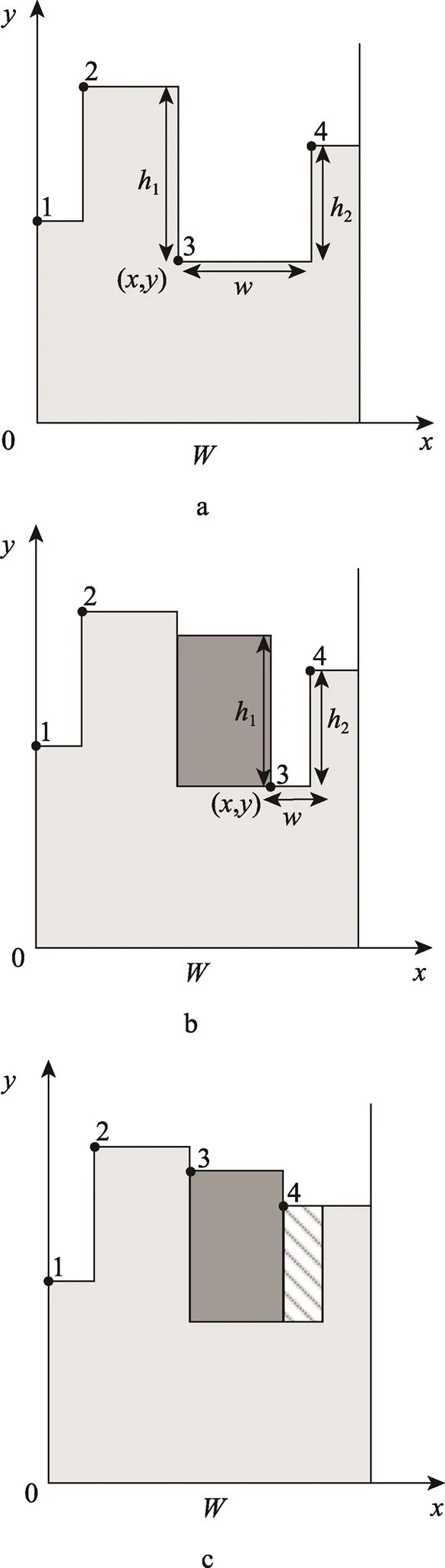
图1 skyline示例

表1 skyline评分规则

Tab.1 Scoring rule employed in skyline

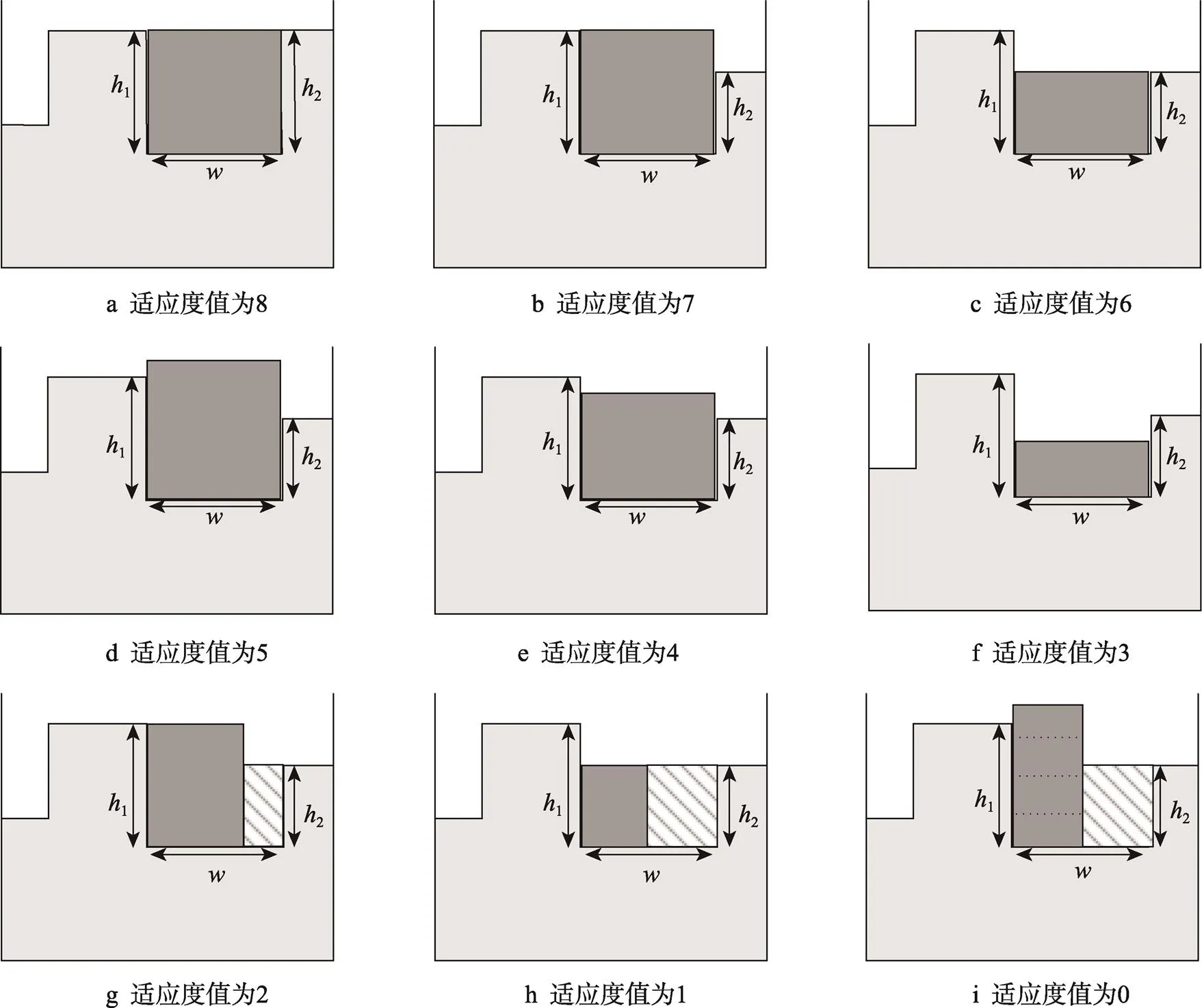
图2 skyline评分规则示例

初始解操作的首要目的是生成一个满足问题约束的解有利于后续目标优化的展开，文中采用均匀分布随机数产生特定范围内符合约束条件的初始编码。编码方式采用3层编码，第1层编码为客户的选择优先度编码，编码长度为，范围是1‒的不重复自然数；第2层为客户待装货物数量编码，编码长度为，范围是1‒的不重复自然数；第3层为装载顺序编码，编码长度为，范围是1‒的不重复自然数。如果，=[1, 3, 2, 2, 4, 3, 2, 1, 1, 3, 2, 4, 3, 1, 2]则1,3,2为第1层编码，表示客户的服务顺序为第1、第3、第2；2, 4, 3为第2层编码，表示第1、3、2个客户的待装货物分别为2、3、4个；2, 1, 1, 3, 2, 4, 3, 1, 2为第3层编码，表示第1个客户的装箱顺序为先第2再第1，第3个客户的装箱顺序为先第1再第3最后第2，第2个客户的装箱顺序为先第4其次第3再第1最后第2。

遗传算法的操作主要涉及轮盘赌选择、交叉交换、变异等，文中为进一步优化算法，主要采用了轮盘赌选择和交叉交换策略。轮盘赌选择操作是以适应度值为选择标准，文中适应度值通过skyline计算空间利用率得出，但是轮盘赌选择操作具有随机性和误差性，因此子代染色体的5%来自于精英选择策略,95%通过轮盘赌方法选择；交叉交换策略为交换客户的服务顺序以及货物的装载顺序。为防止算法过早陷入局部寻优，引入了禁忌表，将局部最优解加入至禁忌表中。设定禁忌长度以及一个常数，在次迭代过程中禁忌访问，每次迭代后。

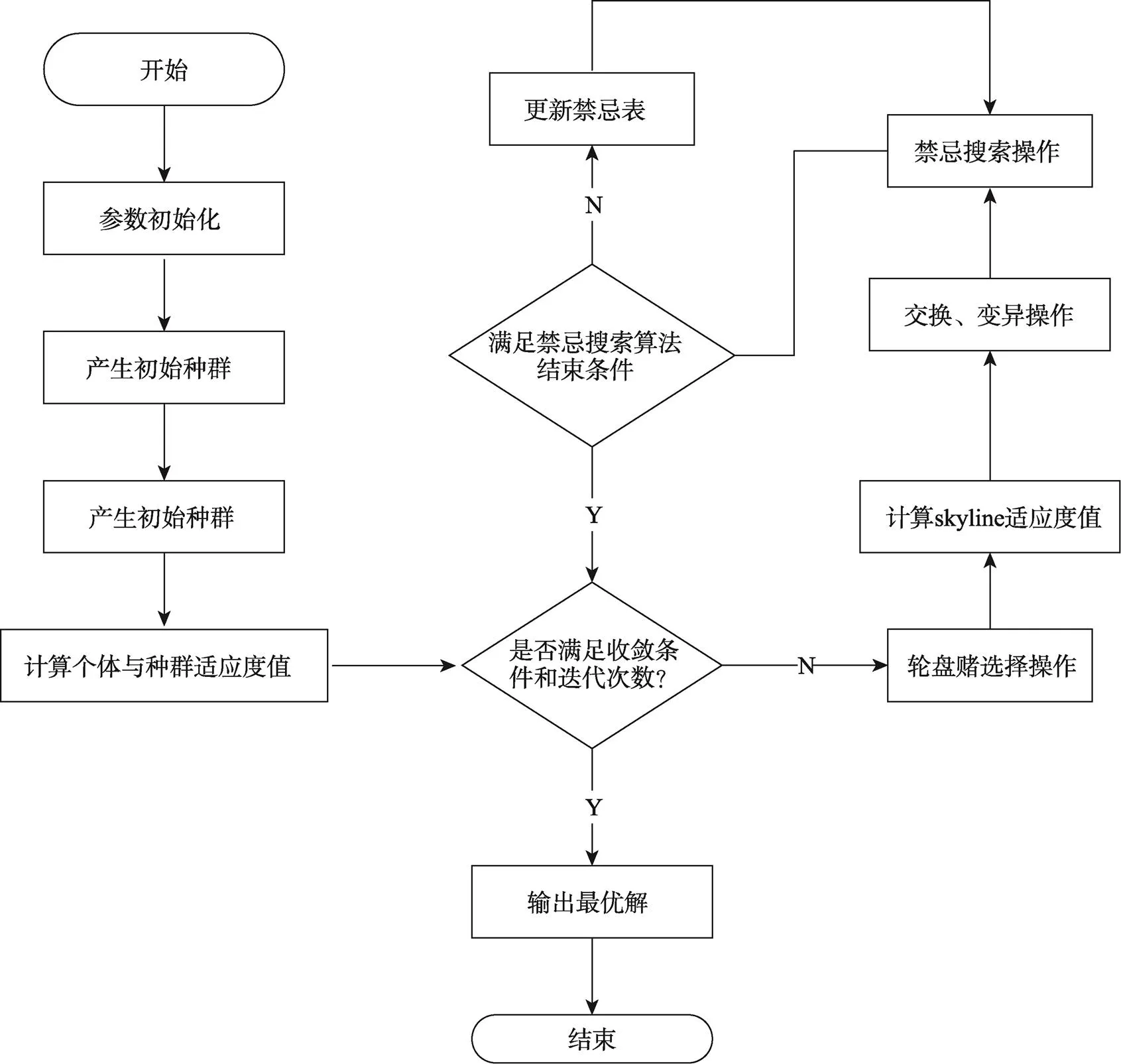
图3 算法流程

3 数值仿真算例分析

3.1 参数设置

为了证明该算法的有效性，现利用数值仿真实验对算法进行实际应用。由于目前没有与本文问题相关的标准测试算例，文中的实验算例由Matlab 9.6.0软件的函数随机生成。服务的客户数量、各个客户的待装、卸货物的数量、尺寸以及质量分别在[5，15]、[0，6]、[300，1500]、[50，500]区间随机生成，尺寸和质量的单位分别为毫米以及千克。设置车的种类为4种，宽度均为180，长度分别为420、760、960以及1 280，对应最大载重分别为2 000、5 000、10 000以及20 000。相关参数设置：初始种群为100，交换概率为0.99，迭代次数为200，禁忌长度=20，常数=50。

3.2 算法验证

算法通过Matlab 9.6.0编程实现，计算机配置为Intel Core i7–9750H、2.60GHz、32GB RAM,在Windows10操作系统下运行。文中用GA–TS算法对随机生成的8个客户算例进行求解，当完成对所有客户的服务后，车上待取货物的装载示意图见图4。

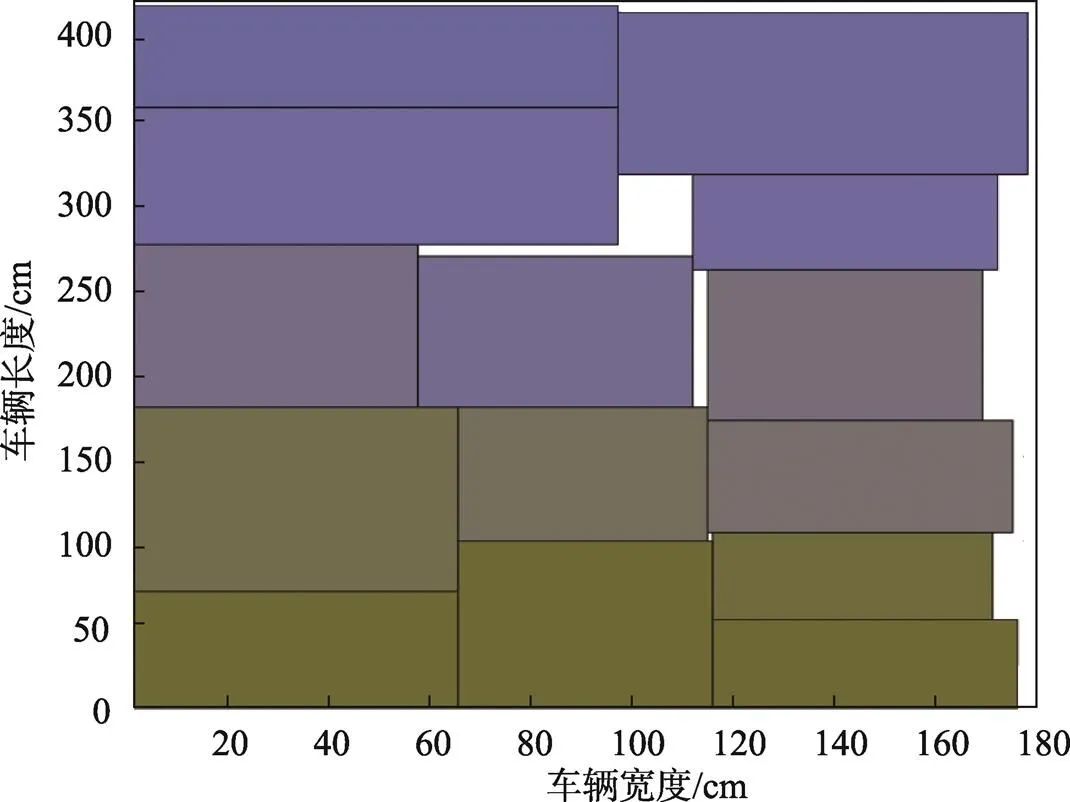
图4 GA–TS算法求解车辆装载示图

表2 8个客户求解结果

Tab.2 Solution results of 8 clients

表2为在为随机生成的8个客户服务过程中车辆处于每一个客户点时车辆的空间利用率和负载状态。由图4和表2可知，针对2–DOPSPD问题，文中提出的GA–TS算法可以较好地解决。在该算法仿真求解结果中为成功完成8个客户的装载配送任务，选取了长度为420 cm的车，平均空间利用率为88.04%，在服务客户4时的空间利用率最低，但是也有79.08%的空间利用率满足实际要求，在服务完客户8时负载达到最大值1 854.54也满足最大2 000的负载上限。

3.3 混合算法优越性分析

为了体现算法在加入了禁忌搜索算法之后，加强了全局寻优能力，文中同时设计了遗传算法作为对比算法进行仿真实验。由于文中研究问题的特殊性，总货物的数量是有限的，若货物量过少时，2种算法均能在同样尺寸的车中寻找到装箱策略，无法体现文中GA–TS算法的优势，而由3.2节随机生成的算例仿真实验中可知，用长度为420 cm的车进行装载任务时空间利用率已接近完全满载状态，因此文中认为3.1节随机生成的算例适合作为算法对比的算例，用遗传算法对该算例求解后所有待取货物的装载状态见图5。

由图5可知，遗传算法在对该算例求解过程中未能在长度为420的车上求得适合的装箱方案，因此只能选择尺寸更大的车辆，选择长度为760的车之后平均空间利用率为48.65%。由此说明，加入了禁忌搜索算法形成的GA–TS算法在解决带同时送取货约束的二维矩形装箱问题中具有优越性。

图5 GA算法求解车辆装载示图

3.4 混合算法有效性分析

为了进一步验证混合算法的有效性，再分别随机生成10、20、30、40个客户的算例，进行多种规模实验分析，考虑到贴近实际，将货物尺寸种类最多为10种，4种规模算例空间利用率比较结果和求解时间见表3。

从表3可以看出，在解决不同数量客户的装载需求时，文中提出的GA–TS算法均能较好的在合理的时间范围内得到空间率较高的装载方案，合理的利用空间，而GA算法求解性能较差，当货物数量接近车空间的临界值时很难求得装箱方案，从而需要采用空间更大的车型。在随机生成10个和30个客户的算例中，尽管与文中所提出的GA–TS算法一样采用了相同尺寸的车，但是GA算法求解所需的时间比文中所提的GA–TS更长。当客户达到40个时，由于文中设定的车辆最大尺寸为1 280，GA算法即使使用最大尺寸的车也无法在适合的时间内求得可行的装箱方案，这也反应GA算法针对复杂算例的求解效率低下，进一步说明文中提出的GA–TS算法实用性好、效率较高，能较好地求解同时送取货的多车型二维矩形装箱问题，图6为40个客户160件待送取货物算例下文中算法求解得到的最终装载示意图，其中待取货物有88件。

表3 多规模算法求解结果对比

Tab.3 Comparison of multi scale algorithm results

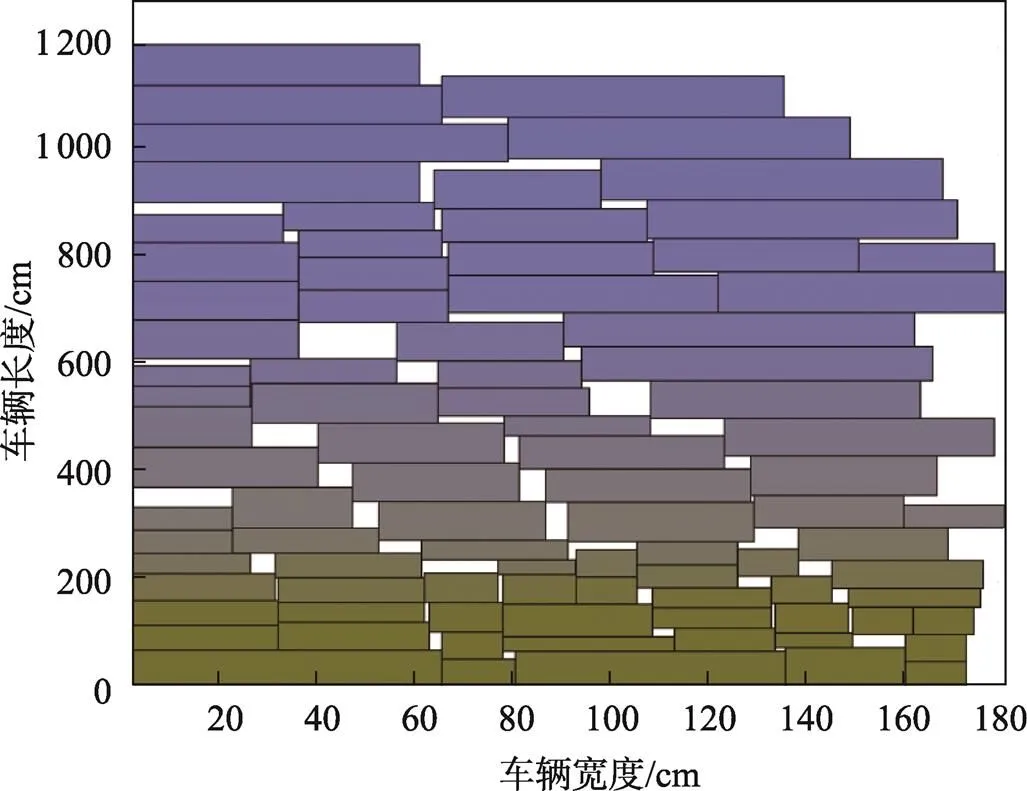
图6 40个客户求解车辆装载示图

4 结语

二维装箱问题是典型的NP难问题，文中为了更贴近实际物流的配送情景，以二维矩形装箱作为研究对象，考虑了在同时送取货约束下设置目标函数，建立货物装载优化模型。针对货物的放置方式，设计了基于skyline的装箱方案，同时根据货物放入的状态给待装货物设置了9种适应度值保证待装区域空间的最大限度利用。针对问题的性质，提出了一种混合算法，将遗传算法和禁忌搜索算法相结合。以遗传算法为基础引入禁忌表，增强算法全局搜索能力，降低陷入局部最优的可能，最终求得满意解。通过文中仿真实验表明，基于带适应度值的skyline装箱方案以及所提算法能有效利用空间，空间利用率较其他算法有明显的优势。在货物装载过程中还可以考虑基于同时送取货的三维装载问题，结合车辆路径问题等方面作进一步拓展。

[1] WEI Li-jun, HU Qian, LEUNG S C, et al. An Improved Skyline Based Heuristic for the 2D Strip Packing Problem and Its Efficient Implementation[J]. Computers and Operations Research, 2017, 80: 113-127.

[2] WEI Li-jun, WANG Yong-sheng, CHENG Hui-bing, et al. An Open Space Based Heuristic for the 2D Strip Packing Problem with Unloading Constraints[J]. Applied Mathematical Modelling, 2019, 70: 67-81.

[3] 黄子钊, 庄子龙, 滕浩, 等. 自动化码头出口箱箱位分配优化超启发式算法[J/OL]. 计算机集成制造系统, 1-26[2021-05-23]. http://kns.cnki.net/ kcms/ detail/ 11. 5946.TP. 20210105. 1515.030. html.

HUANG Zi-zhao, ZHUANG Zi-long, TENG Hao, et al. Optimization of Outbound Container Space Assignment in Automated Container Terminals Based on Hyper-heuristic [J/OL]. Computer Integrated Manufacturing Systems, 1-26 [2021-05-23]. http://kns.cnki.net/kcms/detail/11.5946. TP. 20210105. 1515.030.html.

[4] 张长勇, 翟一鸣, 张倩倩, 等. 考虑装载顺序约束的航空货物装箱问题研究[J]. 包装工程, 2021, 42(1): 150-156.

ZHANG Chang-yong, ZHAI Yi-ming, ZHANG Qian-qian, et al. Air Cargo Packing Considering Loading Order Constraints[J]. Packaging Engineering, 2021, 42(1): 150-156.

[5] 张煜, 程惠敏, 徐进, 等. 考虑堆场派送顺序的混合目的港贝内排箱及其仿真优化[J]. 系统仿真学报, 2018, 30(3): 831-839.

ZHANG Yu, CHENG Hui-min, XU Jin, et al. Simulation Optimization on Multi-Ports Slot Plan Problem Considering Dispatching Sequence of Containers in Yard[J]. Journal of System Simulation, 2018, 30(3): 831-839.

[6] 那日萨, 韩琪玮, 林正奎. 三维多箱异构货物装载优化及其可视化[J]. 运筹与管理, 2015, 24(4): 76-82.

(NA/NUO) Ri-sa, HAN Qi-wei, LIN Zheng-kui. Optimization and Visualization of Multiple 3D Container Loading Problem with Non-Identical Items[J]. Operations Research and Management Science, 2015, 24(4): 76-82.

[7] 李孙寸, 施心陵, 张松海, 等. 基于多元优化算法的三维装箱问题的研究[J]. 自动化学报, 2018, 44(1): 106-115.

LI Sun-cun, SHI Xin-ling, ZHANG Song-hai, et al. Multi-Variant Optimization Algorithm for Three Dimensional Container Loading Problem[J]. Acta Automatica Sinica, 2018, 44(1): 106-115.

[8] 吕雪菊, 倪静. 基于自适应空间划分策略的三维装箱问题[J]. 系统工程, 2020, 38(4): 95-102.

LYU Xue-ju, NI Jing. Three Dimensional Container Loading Problem Based on Adaptive Spatial Partition Strategy[J]. Systems Engineering, 2020, 38(4): 95-102.

[9] RAKOTONIRAINY R G, VAN VUUREN J H. Improved Metaheuristics for the Two-Dimensional Strip Packing Problem[J]. Applied Soft Computing Journal, 2020, 92: 106268.

[10] ARAYA I, GUERRERO K, NUÑEZ E. VCS: A New Heuristic Function for Selecting Boxes in the Single Container Loading Problem[J]. Computers and Operations Research, 2017, 82: 27-35.

[11] 徐小峰, 郑瑶, 邓忆瑞. 考虑同时取送货需求带模糊容量限制的在线设施动态选址问题[J]. 系统工程理论与实践, 2020, 40(9): 2438-2449.

XU Xiao-feng, ZHENG Yao, DENG Yi-rui. Fuzzy Capacitated Online Facility Dynamic Location Problem with Simultaneous Pickup and Delivery[J]. Systems Engineering-Theory & Practice, 2020, 40(9): 2438-2449.

[12] 王超, 高扬, 刘超, 等. 基于回溯搜索优化算法求解带时间窗和同时送取货的车辆路径问题[J]. 计算机集成制造系统, 2019, 25(9): 2237-2247.

WANG Chao, GAO Yang, LIU Chao, et al. Vehicle Routing Problem with Simultaneous Delivery and Pickup Problem Solving by Backtracking Search Optimization Algorithm[J]. Computer Integrated Manufacturing Systems, 2019, 25(9): 2237-2247.

[13] WANG Yong, ZHANG Jie, ASSOGBA K, et al. Collaboration and Transportation Resource Sharing in Multiple Centers Vehicle Routing Optimization with Delivery and Pickup[J]. Knowledge-Based Systems, 2018, 160: 296-310.

[14] 周咏, 计莹峰, 杨华龙, 等. 冷链物流同时送取货车辆路径优化[J]. 数学的实践与认识, 2016, 46(20): 18-26.

ZHOU Yong, JI Ying-feng, YANG Hua-long, et al. Optimization of Vehicle Routing Problem with Simultaneous Delivery and Pickup for Cold-Chain Logistics[J]. Mathematics in Practice and Theory, 2016, 46(20): 18-26.

[15] 谭巍, 文庆. 基于蚁群系统和2-opt方法求解同时送取货车辆路径VRPSPD问题[J]. 数学的实践与认识, 2015, 45(24): 235-242.

TAN Wei, WEN Qing. To Solve the Pickup Delivery Vehicle Routing VRPSPD Problem Based on Ant System and 2-Opt Method[J]. Mathematics in Practice and Theory, 2015, 45(24): 235-242.

[16] GOLSEFIDI A H, JOKAR M R A. A Robust Optimization Approach for the Production-Inventory-Routing Problem with Simultaneous Pickup and Delivery[J]. Computers & Industrial Engineering, 2020, 143: 106388.

[17] 李彤, 崔晶. 不确定需求环境下的路径-装载协同优化研究[J/OL]. 系统工程理论与实践, 1-29[2021-05-23]. http://kns.cnki.net/kcms/detail/ 11.2267.N. 20210203.1445. 008.html.

LI Tong, CUI Jing. Research on Route-Load Cooperative Optimization under Uncertain Demand Environment[J/OL]. Systems Engineering-Theory & Practice: 1-29[2021-05-23]. http://kns.cnki.net/ kcms/detail/ 11.2267. N. 20210203. 1445. 008.html.

[18] 颜瑞, 朱晓宁, 张群, 等. 考虑二维装箱约束的多车场带时间窗的车辆路径问题模型及算法研究[J]. 中国管理科学, 2017(7): 67-77.

YAN Rui, ZHU Xiao-ning, ZHANG Qun, et al. Research Ofthe Model and Algorithm for Two-Dimensional Multi-Depots Capacitated Vehicle Routing Problem with Time Window Constrain[J]. Chinese Journal of Management Science, 2017(7): 67-77.

[19] 尚正阳, 顾寄南, 潘家保. 考虑LIFO装载约束的2L-CVRP车辆路径优化问题[J/OL]. 计算机集成制造系统, 1-22[2021-05-23]. http://kns.cnki. net/kcms/ detail/11.5946. TP.20201202.1710.003.html.

SHANG Zheng-yang, GU Ji-nan, PAN Jia-bao. 2L-CVRP Vehicle Routing Problem with Lifo Loading Constraint[J/OL]. Computer Integrated Manufacturing Systems, 1-22[2021-05-23]. http://kns.cnki.net/kcms/ detail/11.5946.TP.20201202.1710.003.html.

[20] 李珍萍, 刘洪伟, 周文峰, 等. 带装卸顺序约束的装载配送联合优化算法研究[J]. 系统工程理论与实践, 2019, 39(12): 3097-3110.

LI Zhen-ping, LIU Hong-wei, ZHOU Wen-feng, et al. Study on Joint Optimization Algorithm for Loading and Distribution with Loading and Unloading Sequence Constraints[J]. Systems Engineering-Theory & Practice, 2019, 39(12): 3097-3110.

[21] WEI Li-jun, ZHANG Zhen-zhen, ZHANG De-fu, et al. A Variable Neighborhood Search for the Capacitated Vehicle Routing Problem with Two-Dimensional Loading Constraints[J]. European Journal of Operational Research, 2015, 243(3): 798-814.

[22] WEI Li-jun, ZHANG Zhen-zhen, ZHANG De-fu, et al. A Simulated Annealing Algorithm for the Capacitated Vehicle Routing Problem with Two-Dimensional Loading Constraints[J]. European Journal of Operational Research, 2018, 265(3): 843-859.

[23] CORINNA K, FABIAN E J. Axle Weights in Combined Vehicle Routing and Container Loading Problems[J]. EURO Journal on Transportation and Logistics, 2021, 10: 100043.

[24] CÔTÉ J, GUASTAROBA G, SPERANZA M. The Value of Integrating Loading and Routing[J]. European Journal of Operational Research, 2017, 257(1): 89-105.

Optimization of a Two-dimensional Rectangular Packing Problem Based on Simultaneous Delivery and Pickup of Multiple Vehicle Models

CHEN Qi-sai, NI Jing

(Business School, University of Shanghai for Science and Technology, Shanghai 200093, China)

The work aims to study the two-dimensional orthogonal packing problem with simultaneous delivery and pickup, to obtain the maximum average space utilization in the vehicle with consideration of the customers’ demands on the delivery and pickup, the dimension, weight of cargo and multiple vehicles. The hybrid tabu search genetic algorithm (TS-GA) for skyline packing scheme design with nine fitness values was proposed to solve the two-dimensional rectangular packing problem with simultaneous delivery and pickup. During the simulation test, mixing algorithm made the average space utilization in vehicles going to be loaded reach 88.04%, and the packing scheme for simultaneous delivery and pickup of 8 clients was acquired. Based on the hybrid tabu search genetic algorithm (TS-GA) for skyline packing scheme design with nine fitness values, a high space utilization for the two-dimensional rectangular packing problem with simultaneous delivery and pickup is acquired, and at the same time, the research on loading of simultaneous delivery and pickup is improved.

two-dimensional rectangular packing problem; simultaneous delivery and pickup; multiple vehicle models; skyline; hybrid tabu search genetic algorithm

U691+.34

A

1001-3563(2022)19-0226-09

10.19554/j.cnki.1001-3563.2022.19.026

2021–08–27

教育部人文社会科学基金项目（19YJAZH064）

陈其赛（1997—），男，硕士生，主攻智能算法、装载路径。

倪静（1972—），女，博士，副教授，主要研究方向为智能算法、在线社会网络、企业信息化。

责任编辑：曾钰婵