基于皮尔逊层次聚类的马尔可夫优化模型在降水预测中的应用

黄 鹤 高学芳

（宁夏回族自治区水文水资源监测预警中心，宁夏 银川 750001）

水是人类生活生产中必不可少的资源，降水作为主要补给，在自然界水循环过程中有十分重要的意义。但由于降水本身的复杂和多样性，并同时受到气候及人类活动的影响，因而降水系统呈现出非常复杂的特征，这就导致难以进行准确预测。近年来，马尔可夫模型在水文系统预测中取得了快速进展，李娟等应用滑动平均-马尔科夫模型对固原市隆德县进行降水预测，研究证明改进后的马尔科夫模型预测精度较高。韩合忠等利用加权马尔可夫模型对济南市2006、2007两年的降水进行预测，结果均与实际值相符。张志莉以呼伦贝尔市年降水数据为例，构建出滑动无偏残差修正的灰色-马尔可夫组合模型，结果表明，优化模型结果比较理想。

1 研究方法

1.1 马尔可夫模型原理

马尔可夫模型是基于马尔可夫链建立起来的，是一种特殊的随机过程。其数学背景如下：设有一个随机运动的系统，系统在tn+1时刻所处的概率P，只由n 时刻的数据状态决定，与tn-1时刻及之前任意时刻所处状态无关，也即此系统仅与当前状态相关联，与过去状态无关。其数学表达式为：

P（Xn+1=x ∣X0，X1，X2，…，Xn）=P（Xn+1=x ∣Xn）

式中，x 为过程中的某个状态。

1.2 Kolmogorov-Smirnov 检验

K-S 检验法是用于检测一组数据的分布与已知分布二者之间相似程度的一种检验方法，其通过显著性水平来判别二者的相似程度。其数学描述为：设累计频率曲线的理论分布形式为Fe（x），样本的累计频率F1（x）: F1（x）=k/n。式中，n 为总观测数，k 为不大于x 的次数。

给定假设检验H0:F1(x)=Fe(x)，Ha:F1(x)≠Fe(x)

1.3 层次聚类

层次聚类方法是对给定的数据集进行层次分解，当条件满足时可停止。在获得距离值之后，元素之间可进行链接。通过分离和融合构建出一个社区结构。具体过程为：①移除网络里的全部边，得到n 个孤立节点的初始状态；②计算网络里每对节点的相似度；③根据相似度从强到弱连接相应节点对，形成树状图；④根据实际需求横切树状图，获得社区结构。

2 研究区域分布检验

由原始降水数据计算可知，青铜峡水文站81年年降水的期望值为193.3mm，方差为4609.9mm，从而推出P-Ⅲ型分布函数的形状参数α=8.11，尺度参数β=0.04。

由图1得出，经验分布与P-Ⅲ型分布拟合效果最好，趋势均一致且数值较为接近。取置信度a=0.01，n=81，其K-S临界值为0.1811，当假设数据服从P-Ⅲ型分布时，最大偏差为0.1563；发现不能拒绝原假设，所以青铜峡站降水通过了置信度为0.01 时的K-S 检验，符合P-Ⅲ型分布。

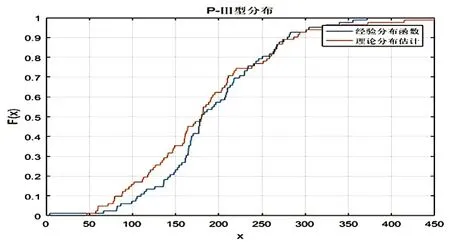
图1 P-Ⅲ型分布函数理论分布对比图

3 模型应用及检验

3.1 降水状态划分

考虑到降水数据的性质和序列数据的结构合理性，对降水数据进行3年滑动平均处理，将滑动平均后的降水时间序列分为5 类，即5 个状态区间。本文使用多种聚类方法进行对比，以选取最优聚类方法。各分级标准具体结果如表1所示。

表1 降水量分级标准 （mm）

3.2 预测结果对比

使用不同聚类方法模型预测结果如表2～表4所示。

表2 水文规范分类法模型检验表

表3 K均值分类法模型检验表

表4 皮尔逊相关系数分类法模型检验表

从以上结果可以看出，基于皮尔逊相关系数的层次聚类划分法为最优状态划分方法，均在允许误差以内，且误差最小。

3.3 未来预测数据验证

由于优化后的马尔可夫模型的预测最终还是要对降水进行长时间预测，所以要确保对未来预测的准确性，还需要进一步验证。通过对原始数据的验证，青铜峡水文站年降水数据更符合P-Ⅲ型分布。所以本文通过对2021—2025年滑动平均降水的预测，再对其结果进行K-S 检验，看其是否满足P-Ⅲ型分布。预测结果如表5所示。

表5 原始数据预测结果

取置信度a=0.01，其K-S 临界值为0.2018，假设数据服从P-Ⅲ型分布，最大偏差为0.0928。通过对比分布的最大偏差与K-S 检验临界值，发现不能拒绝原假设，而且在99%的置信区间上符合P-Ⅲ型分布。所以，对未来5年的降水预测结果是可靠的。

4 结论

（1）依据青铜峡水文站1939—2020年的年降水资料，运用K-S 检验，得出青铜峡地区降水符合P-Ⅲ型分布。

（2）通过对降水数据进行3年滑动平均，采用基于皮尔逊层次聚类法进行状态划分，建立了基于皮尔逊层次聚类的滑动平均-加权马尔可夫链预测模型。

（3）通过对2017年、2018年、2019年、2020年滑动平均降水量的预测及模型验证，得出优化后的马尔可夫降水预测模型可以应用于青铜峡地区降水预测。

（4）对未来5年降水进行预测，预测值分别为199.6mm、200.0mm，184.3mm、208.1mm、193.4mm，通过K-S 检验进行验证，证明了预测的准确性。