考虑库存电池的光储换电站优化充电策略

王子奇，侯思祖，郭 威

（华北电力大学 电气与电子工程学院，河北 保定 071003）

0 引言

电动汽车EV（Electric Vehicle）在新能源消纳、节能减排等方面具有重要的作用，越来越受到学术界的重视和市场的青睐［1］。大容量动力电池产生的充电需求已成为电网的重要负荷之一［2-3］，预计至2030 年电池总容量将达到5.7×109kW·h［4］。EV 补充电能的模式包括充电、换电2种［5］。相较于充电模式，换电模式具有服务耗时短、充电策略灵活的特点［6-7］。可再生能源发电和EV 充电具有良好的契合性［8-9］，有助于提高电网的运行稳定性及降低运行成本［10］。因此，整合分布式光伏PV（PhotoVoltaic）发电和蓄电池储能系统BESS（Battery Energy Storage System）的光储换电站具有广阔的发展前景。

目前，关于换电模式下耗尽电池DB（Depleted Battery）充电的研究主要集中在充电站自身的优化调度［11-12］和对电网的支撑［13-14］方面。然而，大多研究基本上假设换电系统内的电池总数量为定值，未考虑到库存电池数量对优化效果产生的显著影响。库存DB数量的增长可以提高充电策略的灵活性，库存满容量电池FB（Fully-charged Battery）数量的增长有助于保证满足换电的实时需求，但是DB数量的增长和FB 数量的增长均会导致购置成本增大。从换电站运营商角度而言，需要对库存电池数量进行规划。文献［15］指出了一个调度周期（通常为1 d）起始时刻的初始库存电池数量对换电系统运行的重要性，但是其侧重点是优化初始FB总数量以满足换电需求。对于换电站内DB的充电策略而言，在笼统地得到库存电池总数量的基础上，更需要明确初始库存DB 和FB 的最优数量关系，从而为换电站的实际运行提供参考。因此，寻求最优的库存电池配置具有重要的意义。需要说明的是，本文中的库存DB和FB 是指按调度周期起始时刻状态划分的初始库存DB 和FB。此外，换电模式下虽然可以自由安排DB的充电计划，但库存电池与充电、换电行为之间具有内在的时间耦合性，目前鲜有相关研究。为此，本文一方面对库存电池数量进行规划，另一方面对基于库存电池的光储换电站调度运行进行优化，以分析初始库存电池对充电策略和成本的影响。

综上所述，本文重点研究库存电池对光储换电站内电池充电的影响，并将库存电池与换电行为之间的时间耦合性纳入分析范围。首先，建立光储换电站的数学模型；然后，将库存电池按调度周期起始时刻状态细分为DB 和FB 这2 类，分析其时间耦合性的内在机理，提出基于库存电池的充换电约束；最后，在目标函数中计入充电成本和库存电池购置成本，建立光储换电站的充电策略模型，旨在为换电站的优化运行提供理论支持。

1 光储换电站模型

光储换电站的结构示意图如图1 所示。EV 在换电单元产生的DB 被交付至充电单元进行统一充电管理。PV 使得光储换电站的功率来源并不唯一。由于配电网执行峰谷电价，BESS 有助于缓解光储换电站在电价高峰时段面临的充电压力。因此，光储换电站需要综合多方面的信息进行决策，制定充电时间和充电电池数量的调度计划。

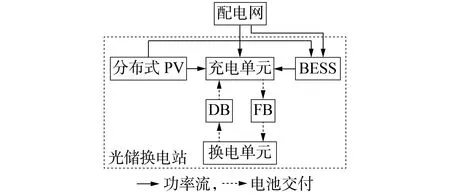
图1 光储换电站的结构示意图Fig.1 Structural schematic diagram of PV-BESS-based battery swapping station

1.1 EV换电模型

本文采用文献［16］中的方法得到1 d 内换电需求均值的时间分布。考虑换电需求的随机波动服从泊松分布［17］，使用蒙特卡罗模拟（MCS）生成各时段的换电需求数量。泊松分布的表达式为：

采用上述方法可生成全天换电需求产生DB 的交付场景。本文生成的交付场景见附录A 图A1。可以看出，1 d内有11:00—14:00和17:00—19:00这2个换电需求高峰时段。

1.2 PV和BESS模型

分布式可再生能源具有出力间歇性特点，已有较多关于PV出力的建模研究，且并非本文的研究重点，因此采用确定性的PV 出力曲线。使用的PV 功率预测值来自Elia Group的公开数据［19］。

BESS的数学模型如下：

2 基于库存电池的充换电约束

2.1 基于库存电池的时间耦合性

换电行为是进行一对一的电池互换，包括库存电池在内的换电站电池总数量是保持不变的。库存电池和换电站的充电、换电行为具有很强的时间耦合性，具体可以概括为以下4个方面：

1）EV 携带的DB 在换电时间之前不能充电，其充电行为必须发生在换电时间之后，但不一定发生在该调度周期（本文取为1 d）内；

2）在一个调度周期的起始时刻，上一周期未充电的DB 转变为该周期的库存DB，可以在周期内的任意时间充电；

3）充电完成之后FB 方可参与换电，且在满足换电需求的前提下，剩余FB 成为下一周期的库存FB，可在周期内的任意时间参与换电；

4）虽然DB的充电时间可以后延，但是由于充电单元的充电能力是有限的（受制于充电机数量、变压器容量等因素），充电时间后延会增加该调度周期无法完成充电任务的风险。

基于上述分析，考虑库存电池时间耦合性的电池数量关系如图2所示。图中，∑tNSWt为单个调度周期内的累计换电EV数量，即累计交付的DB数量，其中部分DB 在该调度周期内完成充电。对于第m个调度周期而言，在第m-1 个调度周期未进行充电的NDB块DB 成为其库存DB，第m-1 个调度周期内的

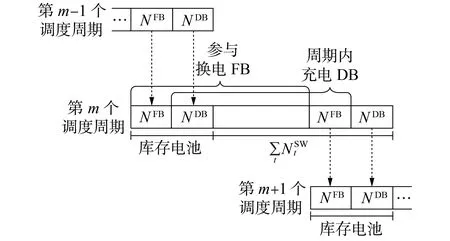
图2 考虑库存电池时间耦合性的电池数量关系Fig.2 Battery quantity relationship considering time coupling of inventory batteries

在一个调度周期内，充电策略必须满足一定的约束条件。本文将库存电池纳入研究范围，充电策略的可行域如图3 所示。令调度周期的总时段数为T，采用累计数量曲线表示各时段的累计充电或换电电池数量，即曲线的一阶差分值为各时段的充电或换电电池数量。

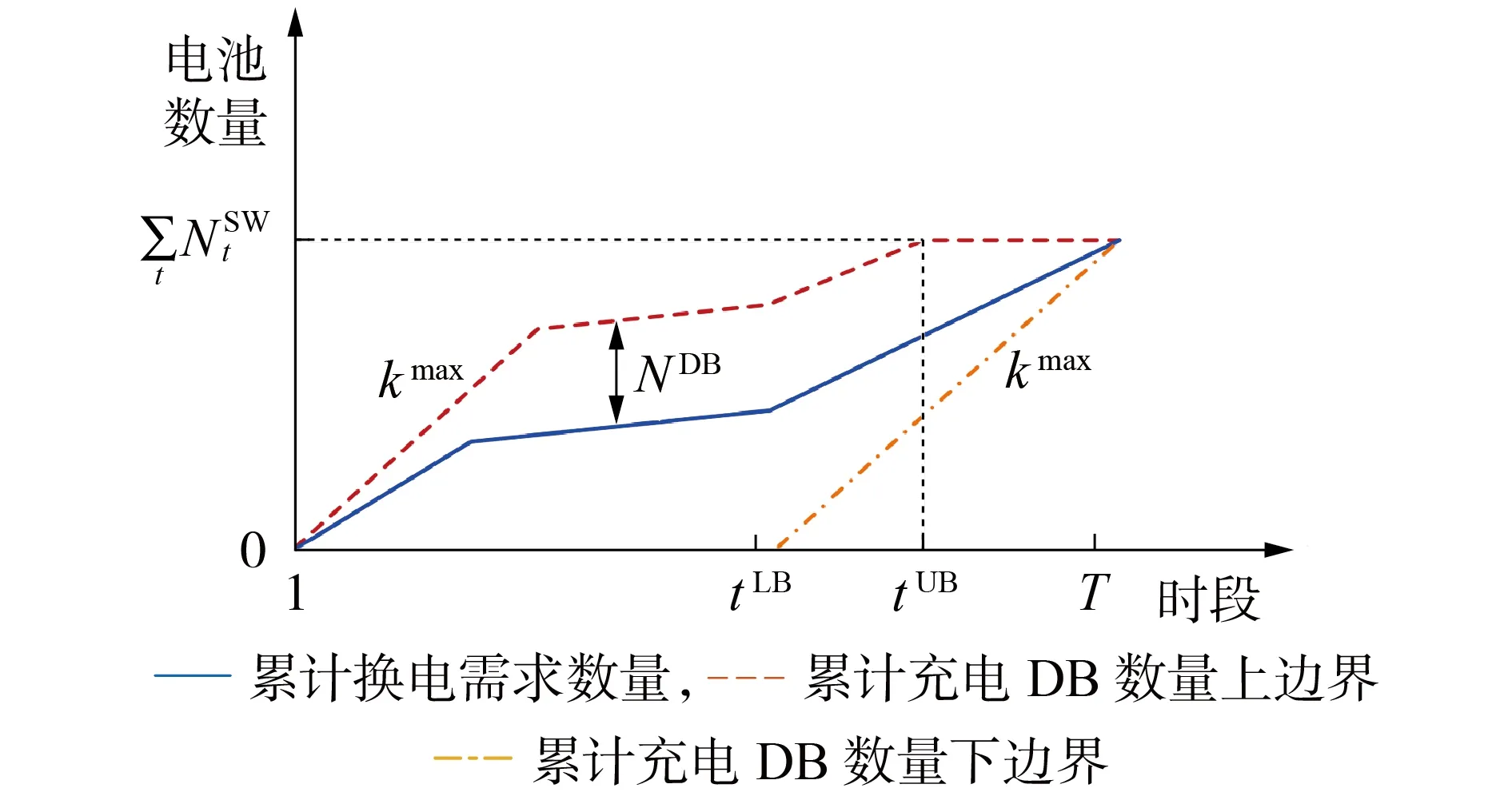
图3 考虑库存电池的充电策略可行域Fig.3 Feasible region of charging strategy considering inventory batteries

由时间耦合性分析可知，任意时段t可以充电的DB 不仅包括库存DB，还包括时段1—t换电交付的DB，所以可充电DB 的数量范围会随着时间的推迟动态扩大。如果在任意时段对所有可充电的DB 立即进行充电，则累计充电DB 数量曲线为NDB与累计换电需求数量曲线的叠加，在时段tUB可完成调度周期内的充电任务，如图3 中的上边界所示。如果所有DB延迟充电，则最迟不能超过时段tLB。考虑到充电能力受充电机数量、变压器容量等制约，继续延迟充电时间会导致周期内的充电任务无法完成。因此，累计充电DB 数量曲线下边界的斜率kmax表征了最大充电能力。上、下边界之间的范围构成了充电策略的可行域，且累计充电DB 数量曲线的斜率k∈[0，kmax]。

2.2 基于库存DB的充电约束

在EV 电池容量EBAT一定的情况下，EVi的DB 充满电所需的充电时长与其SOCSEVi成反比。基于式（2）给出的SOC 概率分布，对充电时长进行离散化，得到：

为了建立基于库存DB 的充电约束，本文引入xi，t、yi、zj，t这3个布尔变量来实现DB充电时间的自由选择，具体含义为：对于调度周期内EVi换电需求产生的DB，如果其在时段t内充电则xi，t=1，如果其未在时段t内充电则xi，t=0；对于调度周期内EVi换电需求产生的DB，如果其在该调度周期内充电则yi=1，如果其未在该调度周期内充电则yi=0；对于库存DBj，如果其在时段t内充电则zj，t=1，如果其未在时段t内充电则zj，t=0。

EV 换电需求产生的DB 的充电时间可以顺延至下一个调度周期，本文采用大M 法建立xi，t与yi之间的关系，如式（5）所示。

式中：t′为考察时段；Ωinv、Ωt分别为库存DB集合、t时段EV 换电需求产生的DB 集合；Nmax，CH为充电机数量。式（7）不等号的左边表示时段1—t′范围内的DB 实际充电时段总数，右边表示时段1—t′范围内所有可充电DB 充满电所需的时段总数；式（8）表示累计充电DB数量下边界的最大斜率约束，不等号左边表示任意时段充电的DB总数量。

库存DB需在调度周期内完成充电，且调度周期始、末的DB数量应保持一致，即需满足：

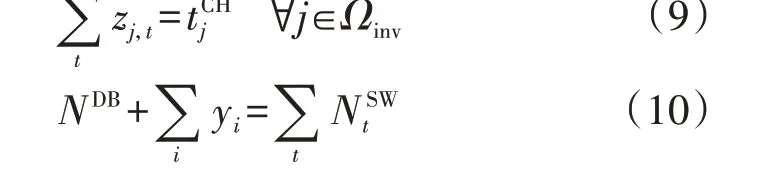
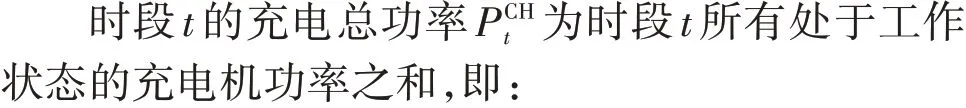
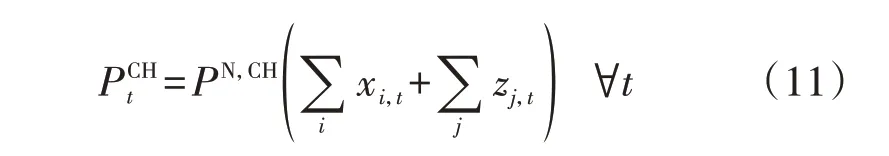
2.3 基于库存FB的换电约束

为了保证光储换电站的稳定运行，充电中心在各时段必须提供足够数量的FB。库存FB 储备可以根据充电策略分配至任意时段使用，但在本调度周期内充电产生的FB 却与换电时间及充电时间相耦合。一方面，对于库存DBj（j∈Ωinv）而言，只要其进行tCHj时长的充电后，就可以作为FB 参与换电；另一方面，对于调度周期内换电需求产生的DBi（i∈Ωt）而言，其只有在换电时间之后进行tCHi时长的充电，才能作为FB参与换电。

故引入ui，t、vj，t这2个布尔变量，分别表示调度周期内换电需求产生的DB 以及库存DB 的充电状态，若充满电则取值为1，否则取值为0，即：

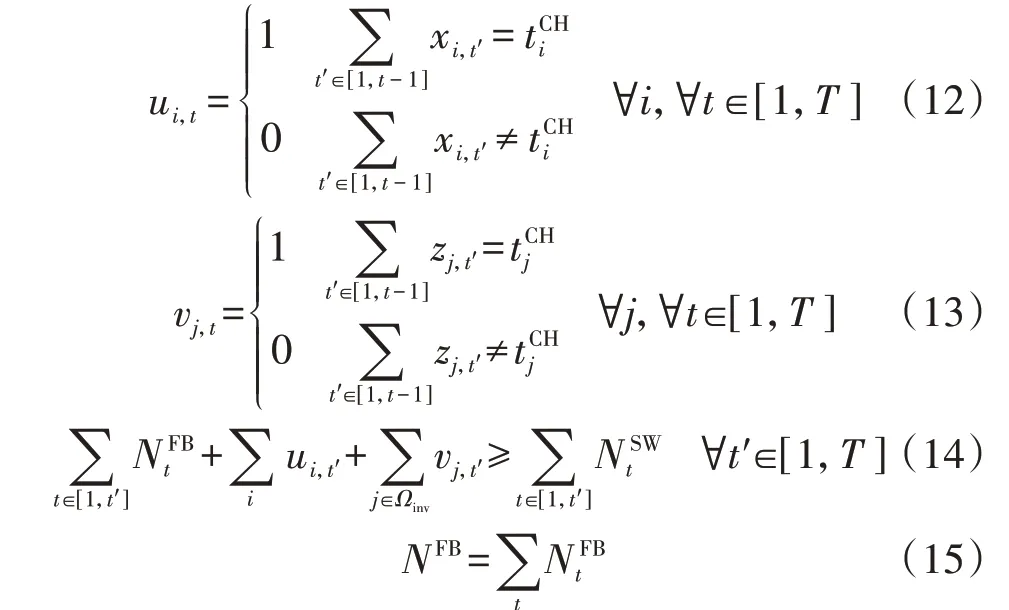
式中：NFBt为时段t用于换电的库存FB数量。式（12）和式（13）表示只有DB 在时段t-1 完成充电，才能在时段t作为FB 参与换电；式（14）不等号的左边第1项表示时段1—t′内用于换电的库存FB总数量，第2项表示时段1—t′内EV 换电需求产生的DB 中完成充电的DB 数量，第3 项表示时段1—t′内充电完成的库存DB 数量，不等号的右边表示时段1—t′内FB总需求数量，则式（14）表示任意时段及其之前时段内的可用FB 总数量必须满足该时段范围内的换电总需求；式（15）表示库存FB总数量为各时段分散使用的库存FB数量之和。

3 光储换电站的优化充电策略

在基于库存电池的充电、换电约束的基础上，建立光储换电站的优化充电策略，从而对库存电池数量进行规划，并优化系统运行调度。由于动力电池的成本是整车成本中占比最大的部分，大规模的库存电池储备虽然可以提高充电灵活性，但会产生高昂的购置成本。因此，需要在库存电池数量和充电成本之间寻求最优的充电策略。

将光储换电站的总成本分为充电成本Cgrid和库存电池购置成本Cpur两部分，优化充电策略的目标函数为最小化总成本，如式（16）所示。

我国相关部门对EV 动力电池的质保期限进行了政策规定［20］，则换电站为EV 装配的动力电池必然是质保期内的合格产品。库存电池即使被闲置，若达到其质保期，则之后将无法用于EV 换电，这会产生巨大的投资成本和社会资源浪费。目前流行的退役动力电池处置办法是将其作为BESS 进行梯级利用。单个调度周期内库存电池购置成本的计算式为：

4 算例分析

本文以1 d为一个调度周期，以30 min为单位时段时长，将单个周期分为48 个时段。根据1.1 节生成EV 换电需求如附录A 图A1 所示，调度周期内共有171 辆EV 参与换电，且EV 均配备62 kW·h 的锂离子电池（数据来源于2021 款Nissan Leaf）。光储换电站安装了容量为400 kW 的PV 以及额定容量为1 500 kW·h 的BESS，配置了25 台充电机，单机充电功率为25 kW。采用北京市10 kV 电压等级的一般工商业电价。PV 功率和分时电价见附录A 图A2。其他仿真参数见附录A表A1。

4.1 库存DB优化结果分析

4.1.1 灵敏度分析结果

对不同NDB下的总成本进行灵敏度分析，结果如图4所示。由图可知：当NDB＜40块时，随着NDB增大，充电成本快速减小，所以总成本单调递减；当NDB增大至40～70 块范围内时，充电成本的减小空间越来越小，而库存DB数量过多会导致电池购置成本在总成本中占据较大的比例，使得充电成本和库存电池购置成本均会对最优充电策略产生较大的影响；当NDB＞70块时，充电成本达到下限而库存电池购置成本仍增大，所以总成本快速增大；当NDB=48块时，光储换电站的总成本达到最小值（即库存DB最优数量NDB*=48块）。

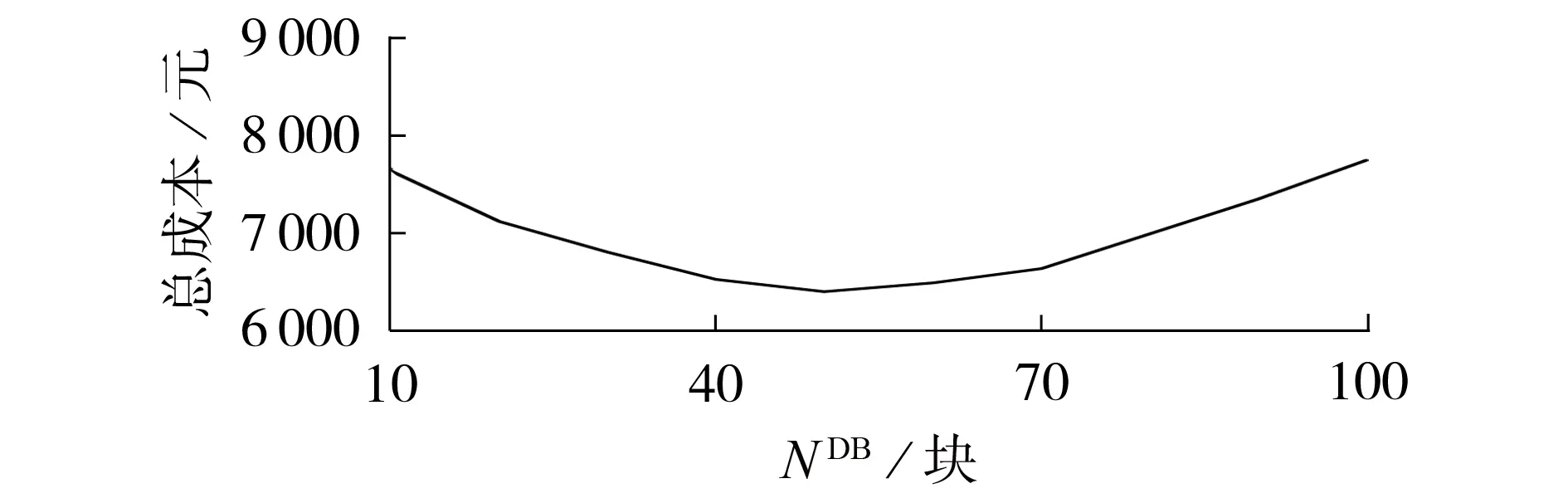
图4 总成本的灵敏度分析Fig.4 Sensitivity analysis of total cost

通过仿真发现，当NDB≤7块时，不存在可行的充电策略。这是因为NDB过小会导致充电策略过度依赖于DB的交付时间，在换电需求高峰时段之后会产生过多的待充电DB，但受限于可行域的下边界，调度周期内的充电任务将无法完成。

充电成本和库存电池购置成本的灵敏度分析结果见图5。由图可知：当NDB介于10～60 块之间时，峰时段负荷转移至谷、平时段，充电成本整体呈下降趋势；当NDB≥70 块时，在累计充电DB 数量上、下边界范围内的充电潜力已经被最大化利用，继续增大NDB数值并不会改变充电策略，充电成本收敛于3 751.72 元；库存电池购置成本与NDB基本保持正相关，但是当NDB≤40 块时，库存电池购置成本的上升速率明显低于充电成本的下降速率，造成总成本减小。

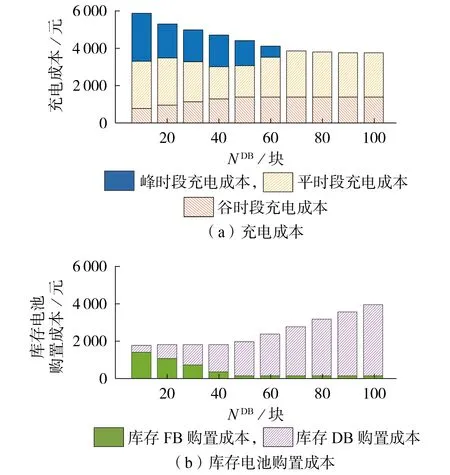
图5 充电成本和库存电池购置成本的灵敏度分析Fig.5 Sensitivity analysis of charging cost and inventory battery purchase cost

4.1.2 充电策略对比分析

为了分析库存电池数量对总成本的影响原因并验证本文所提优化策略的有效性，在仿真中根据NDB取值设置以下3 种场景进行对比分析：①场景1，初始库存DB 数量为灵敏度分析结果所得的最优数量NDB*；②场景2，换电站内只具备较少的初始库存DB，设定NDB=NDB*-30；③场景3，换电站内具备大量的初始库存DB，设定NDB=NDB*+30。上述3 种场景的优化充电策略见附录A图A3，充电成本见表1。

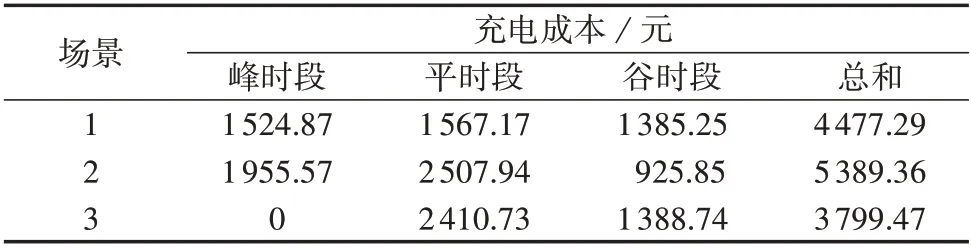
表1 3种场景的充电成本Table 1 Charging cost of three scenarios

由图A3可以看出，3种场景都实现了PV发电功率的最大化利用。由表1 可以看出，相较于场景2，场景1、3 的充电成本分别下降了16.92%、29.5%，表明NDB和充电成本成反比，主要原因有如下两方面。一方面，比较附录A 图A1 和图A2 可知，换电需求和电价波动在总体趋势上基本保持一致。时段1—14为电价谷时段，而该时段内的换电需求较少，导致调度周期内由换电交付的DB 产生的充电功率很小。场景2 的库存DB 较少，所以谷时段的充电能力利用率很小。随着库存DB数量的增大，谷时段的充电潜力逐渐被释放。另一方面，由于累计充电DB数量下边界的限制，当库存DB 较少时，在调度周期的后期将面临巨大的充电负担。场景2 因前期在谷时段的充电能力利用率较小，为了完成调度周期的充电任务，在中后期基本保持满负荷充电，在时段23 之后，即使PV出力较低，也不得不从配电网高价购入大量电能。整体充电时间分布的后移导致充电成本大幅上升，且加剧了电网负荷峰谷差。相较而言，场景1、3 因在前期完成了更多的充电任务，在峰、平时段的充电策略更加灵活。相比场景2，场景1、3分别有13.75%、17.15%的充电负荷从峰时段和平时段转移至谷时段。

随着NDB增大，充电策略逐渐与EV 换电交付DB 的时间解耦，对分时电价的利用能力增强。充电时间分布随NDB的增大而整体前移，减轻了电网负荷高峰时段的充电压力。这对于提高新能源的消纳比例和电网削峰填谷具有积极的作用。但是通过对比发现，虽然场景1 的总成本最小，但其充电成本相比场景3 仍有下降空间。这表明在考虑库存DB 数量时，充电策略并非是完全利用分时电价机制的。单纯追求充电成本最小化会导致库存电池购置成本增大，从而使总成本偏离最优值。上述结果验证了本文所提优化充电策略得到的最优库存DB 数量的有效性。

4.2 DB、FB的相关性分析

根据充电模型，DB与FB之间存在关联。3种场景下各时段的库存FB 需求数量如附录A 图A4 所示。由图可以看出，3 种场景下主要是换电高峰时段的库存FB 需求数量有所差别。当NDB较小时，2个换电高峰时段需要大量的库存FB 来填补充电产生FB 的不足；当NDB较大时，通过谷时段充电在初期积累了更多的FB，在换电高峰时段所需的FB 更大程度上来自于调度周期内充电产生的FB，多余的库存FB只会造成库存电池购置成本增大。

图5 所示灵敏度分析结果验证了库存DB 和FB在数量上存在负相关关系。值得注意的是，库存FB购置成本最终并未收敛至0，这是因为在调度周期开始阶段所有DB均未充电完成，必须通过一定数量的库存DB来满足换电需求。

4.3 库存DB对BESS运行的影响分析

不同NDB下的最优充电策略不同，因此光储换电站内的BESS在各时段的充放电策略也有所区别。本文从SOC 变化和循环次数两方面分析BESS 的运行状况。定义调度周期内BESS 的循环次数fBESS的计算式为：

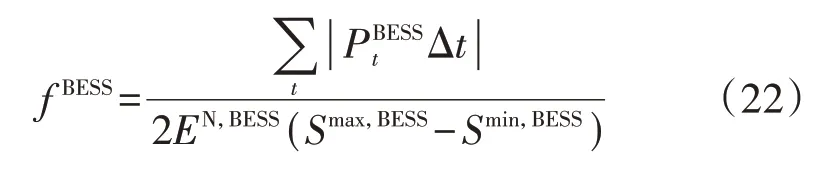
3 种场景下调度周期内BESS 的SOC 变化曲线及其循环次数的灵敏度分析结果分别见附录A 图A5 和图A6。由图A5 可以看出，库存DB 数量越大，BESS 的利用率越低。3 种场景下BESS 在时段32 之前的运行策略基本相同，之后开始出现差别。由图A6 可以看出，随着库存DB 数量增大，fBESS呈现先升后降的趋势。BESS 首先利用夜间的谷时段电价将SOC 提升至上限，其能量在第1 个电价峰时段被大量消耗。由于调度周期始、末的SOC保持平衡，如果在第2 个电价高峰时段继续保持长时间高功率放电，则必须要在调度周期末的平时段和谷时段进行充电。当NDB较小时，调度周期末面临着巨大的DB充电压力。此时PCHt=Pmax，GRID，BESS 无法从配电网获得充电功率，导致第2 个电价高峰时段的放电能力受到制约，fBESS较小。随着NDB增大，调度周期末的DB 充电压力得到缓解，BESS 在第2 个电价高峰时段的放电深度更大，fBESS逐渐增大并稳定在1.6。但当NDB较大时，有更多的DB在时段14之前的谷时段完成充电，在高峰时段DB 的充电压力很小，导致DB 充电策略与电价的耦合性更强。由附录A 图A3（c）可以看出，2 个电价高峰时段的功率需求大幅降低，BESS 的削峰填谷作用被弱化，因此fBESS逐渐减小。

当NDB=48 块时，总成本最小，此时fBESS处于上限，表明BESS对降低总成本及削峰填谷具有重要的作用。

5 结论

本文研究了换电站内电池充电过程中的库存电池数量问题，重点考虑了库存电池与换电行为之间的时间耦合性，所得主要结论如下：

1）库存电池数量会对换电站的运行产生重要的影响，所提基于库存电池的充电、换电约束能正确反映光储换电站的运行特性；

2）所提优化充电策略综合考虑了电网充电成本和库存电池购置成本，有助于电网的削峰填谷和降低换电站的运行成本；

3）随着库存DB数量增大，充电成本和最低库存FB 数量减少，电池购置成本和BESS 循环次数增大，换电站在运营过程中执行最优的库存电池配置方案能保证调度措施的有效性。

附录见本刊网络版（http：//www.epae.cn）。