放慢探究脚步,经历抽象过程
——“有余数的除法”一课教学实录与评析
●赵绪昌,熊荣华
2022年4月19日,四川省达州市通川区第七小学校举办的“促进理解与迁移”青年教师数学教学展示活动,其中“有余数的除法”一课,教学效果好。现将本节课的主要教学实录陈述如下。
一、创设情境激兴趣
师: 孩子们, 告诉你们一个秘密——我有超能力。(学生疑惑)不信?看,屏幕上这么多的珠子,你随便说一个数,我不看屏幕,就知道这个数对应的珠子是什么颜色。 (如图1 请学生说数,老师猜颜色)
生1:26。
师:红色。
生2:15。
师:紫色。
……
师:想不想拥有这样的超能力?认真学习这节课,你们也会变得这么厉害。
二、分类游戏埋伏笔
师:老师今天还给大家带来了这4 类游戏(如图2),它们分别是:

图2
师:瞧,有10 个小朋友来打乒乓球,每2 人一组,可以将他们分成几组? (如图3)

图3
生:可以分成5 组。
师:刚好分完,没有剩余。 他们还想玩剩下的这三种游戏, 你能帮他们分分组吗? 请拿出学习单一(如图4),动手圈一圈。

图4
(学生完成学习单一,教师巡视,拿一张学习单,投影展示)
师:这是生1 的分组情况(如图5),你们赞成吗?

图5
生:赞成。
师:根据这样的分组情况,你能将这些游戏分分类吗?
生1:刚好分完的分为一类,还有剩余的分为一类。
生2:第1 种和第4 种刚好分完,第2 种和第3种还有剩余(如图6)。

图6
师:用数学的眼光仔细观察,不管是正好分完,还是有剩余, 分得的每份都同样多, 每份分得同样多,这种分法在数学上叫——(课件展示,如图7)

图7
生:平均分。
三、整除除法垫基础
师:10 个小朋友, 每2 人一组, 平均分成了几组? 用算式怎么表示?
生:10÷2=5(组)。
师:这个算式表示什么意思?
生:10 个小朋友,每2 人一组,可以分成5 组。
师:那每5 人一组,又平均分成了几组?
生:10÷5=2(组)。
师:这个算式又表示什么意思?
生:10 个小朋友,每5 人一组,可以分成2 组。
四、有余除法拔新高
师:平均分,正好分完,我们可以用除法算式来表示。 那像这种平均分后,还有剩余,用算式怎么表示呢?
(黑板张贴:10 个小朋友,每3 人一组,可以分成3 组,还剩1 人)
师:你能用一道算式表示出题目的意思吗?请拿出学习单二看到第一题(如图8),试着写一写。
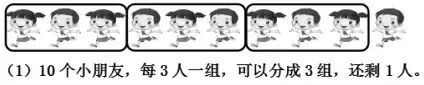
图8
(学生试写,教师巡视,收集题单,请学生上台,投影展示)
师:老师收集了这几种不同的算式,我们一起来听听他们的想法。
生1:我列的算式是:3×3+1=10(个),每3 人分一组,分成了3 组,加上剩余的1 人,一共有10 人。
生2:我列的算式是:10-3-3-3=1(人),10 个小朋友,减去3 个3 人,还剩余1 人。
生3:我列的算式是:10÷3=3(组)剩1(人),10个小朋友,每3 人一组,可以分3 组,还剩1 人。
生4:我列的算式是:10÷3=3(组)……1(人),10个小朋友,每3 人一组,可以分3 组,还剩1 人。剩余的1 人用省略号更简洁。
师:(请生下台,并板书)10÷3=3(组)……1(人)
师:看到这个全新的算式,你们有什么想要了解的?
生1:这个算式表示什么意思?
生2:10 个小朋友,每3 人一组,可以分成3 组,还剩1 人。
生3:这个算式怎么读呢?
生4:10 除以3 等于3 余1。
生5:我觉得加上单位更好,10 除以3 等于3 组余1 人。
生6:在除法算式中,余下的这个数叫什么呢?
生7:余数。
师:好的,咱们就叫它余数。
10÷3=3(组)……1(人)
(板书:被除数 除数 商 余数)
师:这道除法算式与以前学的有什么不同?
生:以前学习的除法算式没有余数,今天学习的除法算式有余数。
师:今天我们就一起来学习有余数的除法。
(板书:有余数的除法)
师:10 个小朋友,每4 人一组呢? 用算式怎么表示? 看到学习单二第2 题(如图9),动手写一写。

图9
生:10÷4=2(组)……2(人)
师:这个算式表示什么意思?
生:10 个小朋友,每4 人分一组,分成2 组,还剩2 人。
五、余数除数比大小
师:这2 个小朋友被余下,成了这道除法算式中的余数。 要是来更多的小朋友,每4 人一组,余数还可能是几呢? 老师为你们准备了人数不一样的学习单三(如图10),同桌两人合作,先圈一圈,再列算式。

图10
师:你们找到的余数分别为几呢?
生1:总人数分别为9,10,11,12 时,我们找到的余数为1,2,3。
生2:当总人数为13,14,15,16 时,我们找到的余数有1,2,3。
生3:当总人数为17,18,19,20 时,我们找到的余数为1,2,3。
生4:当总人数为21,22,23,24 时,我们找到的余数有1,2,3。
师:人数不一样,每4 人一组,余数始终为1,2,3,这里面藏着什么数学奥秘呢?我们一起来探个究竟。 (课件逐一展示,如图11)

图11
师:每4 人一组,余数可能为——
生:1,2,3,4。
师:余数为4,你们刚才怎么就没有找到呢?
生1:余下的4 人又可以分成1 组啦!
生2:就算来再多的小朋友,每4 人一组,余数只可能为1,2,3。
师:如果每5 人1 组呢? 余数可能为——(课件展示,如图12)

图12
生:1,2,3,4,不余5。
师:为什么不余5?
生1:余下的5 人又可以分成1 组。
生2:就算来再多的小朋友,每5 人一组,余数只可能为1,2,3,4。
师:每10 人1 组呢? 余数可能为——
生:每10 人1 组,余数可能为1 到9。
师:每100 人一组呢? 余数可能是——
生:每100 人1 组,余数可能为1 到99。
师:请用一句话概括余数和除数的大小关系。
生1:除数比余数大。
生2:余数不能等于除数。
生3:余数比除数小。 (板书,如图13)

图13
六、闯关练习固新知
师:你是否已具备拥有超能力的资格,你还得成功通过下面这三关。
第一关:
(1)11÷2=4……3。 ( )
生:错。
师:3 比4 小呀,哪儿错了呢?
生:余数要比除数小,不是比商小。
(2)在有余数的除法中,只要余数不大于除数就行。 ( )
生:错,余数不仅不能大于除数,还不能等于除数。
(3)有算式☆÷6=○……△中,△最大为6。( )
生:错。 因为余数比除数小,这里的余数和除数相等了,所以是错的。
第二关:
师:这只青蛙遮住的余数,最大是几?

图14
生:余数最大是5。 因为除数是6,余数比除数小,余数最大就是5。
师:分析得真到位。瞧,真是5。那这只青蛙遮住的除数最小是几呢?
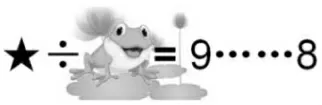
图15
生:这里的除数最小是9。因为余数是8,余数比除数小,那除数最小就是9 啰!
师:你的思路真清晰。 看,果真是9。
第三关:

图16
师:孩子们,仔细观察这些珠子的颜色,你有什么发现?
生1:它们是按红橙黄绿紫为一组,不断地重复出现的。
生2:余1 是红色,余2 是橙色,余3 是蓝色,余4 是绿色。
师:请问第15 颗珠子是什么颜色?
生:紫色。
师:第26 颗珠子呢?
生:红色。
师:第18 颗珠子呢?
生:蓝色。
师:呀! 你们也拥有超能力啦。 原来解锁超能力的钥匙,就是这节课学习的有余数的除法。在我们的生活中,像这种平均分后有剩余的情况还有很多,你能举一个用有余数的除法来解决的数学问题吗? 同桌两人合作,试着说一说。
(学生合作完成)
二年级学生第一次学习“有余数的除法”,而有余数的除法涉及的数量关系相对复杂。 本节课通过让学生经历分东西的活动,先形成有“余数”的表象,在此基础上逐步建立“余数”“有余数除法”的概念及“余数比除数小”的结论,为下一步学习有余数除法试商打下良好的基础。概念本质上是一种分类行为,分类的过程就是事物抽象的过程。 为了让学生深刻把握概念的本质,教师在教学时尽量不直接告知,而是引领学生经历操作、观察、分类、抽象、概括的过程,从而形成概念。 老师的教学设计,主要帮助学生建立余数的概念,初步理解有余数除法的意义和知道余数必须比除数小。无论是新课教学,还是课堂练习,授课老师都紧紧抓住余数的意义和余数要比除数小的重点和难点展开。教学中,老师加强了直观教学,充分利用学习单,让学生在图上圈一圈,让学生在操作过程中确实感觉到平均分物体时,余数存在的客观性和产生过程。如此教学,“算理”与“算法”同时进行,比翼齐飞,学生的运算能力和抽象能力等在问题情境中得到形成与发展。

