闸坝下游局部冲刷计算方法的对比分析

高 翔

(徽县水务局，甘肃 陇南 742300)

对于山区河流来说,由于中低水头闸坝工程的修建,抬高了上游水位,与下游水位形成了一定的水位差,过闸水流经泄水建筑物后把势能转换成巨大的动能[1]。中低水头闸坝工程的消能措施一般为底流消能,虽然有护坦、海漫等消能措施,但水流的流速仍然很大,达到泥沙的起动流速从而将下游泥沙冲向河道下游,形成了闸坝下游的冲刷坑[2]。

为了确保闸坝式水电站的安全运行,避免危及工程安全的情况发生,准确预测闸坝下游的冲刷深度对工程安全运行具有极其重要的意义[3]。目前针对闸坝工程下游的局部冲刷问题已有很多研究成果,但各家公式之间的计算结果相差较大,主要是由于所依据的分析理论、研究方法、实测资料来源不同等因素造成的[4]。本文在对比分析前人研究的基础上,以毛昶熙的剪切应力推导公式为依据,推导出了一种计算闸坝下游局部冲刷深度的计算公式,并选取其他水电站下游冲刷坑实测资料进行了验证。

1 闸坝下游局部冲刷不同计算方法的归纳

根据现有公式的分析理论、研究方法、资料来源的不同,本文选用较有代表性的7类冲刷公式进行对比分析。

1.1 引用普遍冲刷公式

我国学者王艺雄调查研究了淮河上的水闸冲刷观测资料,得到的冲刷坑深度计算公式为[1]

式中:q为闸下游主流宽度上的单宽流量,m2/s;K为经验系数,与河床土质和水流的挟沙情况有关。

1.2 引用不冲流速公式

《水闸设计规范》(SL 265—2001)中引用的水流出海漫末端冲刷坑深度公式为

式中:T为海漫末端最大冲刷坑上水深,m;qm为海漫末端单宽流量,m2/s;v0为河床允许不冲流速,m/s。

1.3 借助急流扩散理论的局部冲刷公式

国外学者维兹果从急流扩散理论出发,引入了发生水跃的共轭水深计算公式,通过多组模型试验数据,得到了冲刷坑上水深公式[1]:

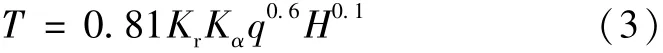
式中:T为冲刷坑上水深,m;H为上下游水位差,m;Kr为土质情况;Kα为出流的倾角;q为下泄单宽流量,m2/s。

1.4 指数形式的试验公式

我国学者施振兴推导出了适用于消能戽下游河床冲刷坑计算的公式[1]:

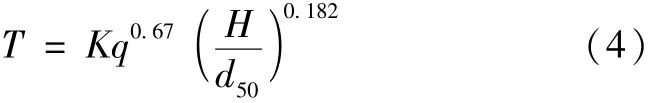
式中:q为下泄单宽流量,m2/s;K为经验系数,与淹没度、戽长比、戽末端挑角等有关;H为上下游水位差,m;d50为下游河床泥沙中值粒径,m。

1.5 从输沙率推导的冲刷公式

从水流输沙率出发可以推导出随时间变化的下游局部冲刷深度计算公式[5]:

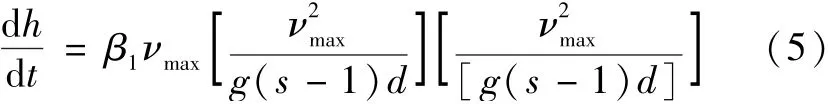
式中:β1为无尺度的系数。

1.6 考虑河床粗化的冲刷公式

尹学良、万兆惠等依据非均匀沙河床粗化的原理,对永定河官厅水库下游形成的典型粗化层特性的认识,通过研究抗冲粗化层所需要的厚度、形成的粗化层泥沙颗粒所占百分数等因素,建立了基于粗化理论的河床冲刷的极限深度计算公式[5]:

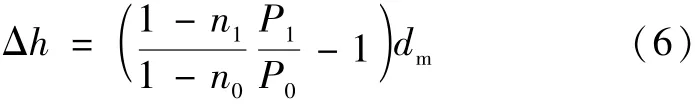
式中:P0为粗化层颗粒的重量占原始河床组成总重量的百分数;P1为粗化颗粒的重量占粗化层总重量的百分数;n0、n1分别为原始河床组成和粗化层的孔隙率;Δh为冲刷深度,m;dm为粗化层厚度,m。

Research on indoor floor characteristics and suitable restoration technology of Qingtao German-style historic buildings

1.7 从剪切应力推导的冲刷公式

毛昶熙从水流对河底的剪切应力出发推导出下游局部冲刷深度计算公式,然后考虑了水流流态和相对水深这些因素对公式进行修正[6]:

式中:ψ为冲刷经验系数,闸坝下游一般取0.66;α为流速分布不均匀动量修正系数,一般取1～1.5;y为护坦末端垂直流速的最大值距地面的高度,m。

2 各冲刷公式对比与分析

2.1 各家公式量纲和谐分析及适用情况分析

本文所列的七大类公式,各自依据的理论不同,推导方法不同,各系数都是按照各自所参考的河流及模型试验所得,适用条件不同,每种公式计算所得的差距较大[7]。

式(1)中的系数都根据特定河流水流条件进行确定,虽然公式左右量纲不和谐,但是计算简单。该公式只适用于河道普遍冲刷情况,一般不具有局部冲刷的普遍适用性。

式(2)左右量纲和谐,若有可靠的不冲流速数据,则计算较为简单。该公式只考虑了河床的土质和河流下泄单宽流量,并且由于对枢纽消能设施、闸门开启方式、高速水流流出消力池时的流态等因素没有考虑,计算出的冲刷坑深度误差较大。

式(3)和式(4)考虑了单宽流量、上下游水位差等影响因素,施振兴公式还引入了泥沙颗粒粒径的因素等,虽然左右量纲不和谐,但计算不复杂。因为只考虑了影响冲刷最主要的因素,计算结果与实测数据有一定偏差。

式(5)从输沙率出发推导出的冲刷深度计算公式,根据模型试验资料来确定系数。经计算与实测资料比较,吻合情况较好。但是该公式计算较为复杂。

式(7)毛昶熙从剪切应力推导出的冲刷关系式所考虑的因素,既包括河床的单宽流量、河床质的密度等因素,又包含了水流流态和相对水深这些修正因素,具有较为广泛的代表性,适用性较好,且量纲和谐。

2.2 基于剪切应力下一种新的闸坝下游局部冲刷公式推求

经以上分析研究,选取适用性较好,具有广泛代表性的毛昶熙公式,以二元水流为基础进行推导,考虑水流内部为静水压力分布时,沿水平方向的水流动量方程式为[1]

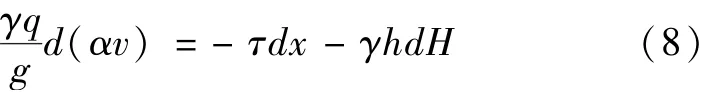
式中:q为单宽流量,m2/s;v为断面平均流速,m/s;τ为主流与漩涡分界面上的剪切应力,N/m2;h为漩涡分界面以上的水流深度,m;H为水面高度,m;α为流速分布不均匀性的动量修正系数;γ为水的重度,N/m3。

根据毛昶熙的计算推导,引入泥沙开始被冲动时的平均流速或起动流速vc,推导出的冲刷坑上水深计算公式为

关于泥沙起动流速的计算公式,目前的研究还是以经验公式或者半经验半理论为主,采用沙莫夫公式来计算起动流速[1]:

一般计算的泥沙为天然无黏性泥沙,因此沙莫夫公式可简化为

将式(11)代入式(9)计算得冲刷坑上水深T为

为了确定系数ψ,参考已有的水工模型试验冲刷试验数据,选用偏桥水电站、麒麟寺水电站的资料进行计算[5],计算结果见表1。

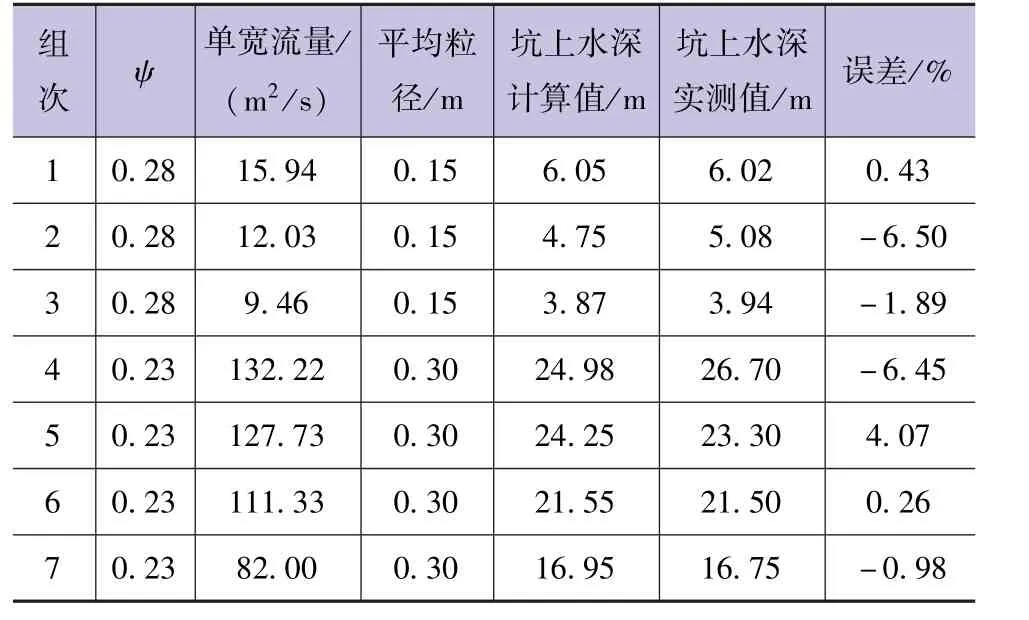
表1 计算中流态参数的取值

计算结果表明,系数ψ取值分别为0.23、0.28时,计算结果与实测冲刷坑上水深误差均在7%以内,误差的平均值为2.94%,在理想的范围内。

因此,式(12)系数ψ初步取值为0.23～0.28。

2.3 本文公式验证

为了验证本文所推导公式的适用性,参考已有工程数据资料,选取横丹水电站[8]、黄丰水电站[9]、锁儿头水电站[10]、巨亭水电站[4]、潼南航电枢纽工程[5]、利泽航运枢纽工程[5]、当卡水电站[11]7个工程的43组冲刷资料进行验证,结果见表2,将计算值和实测值结果点绘于图中,见图1。

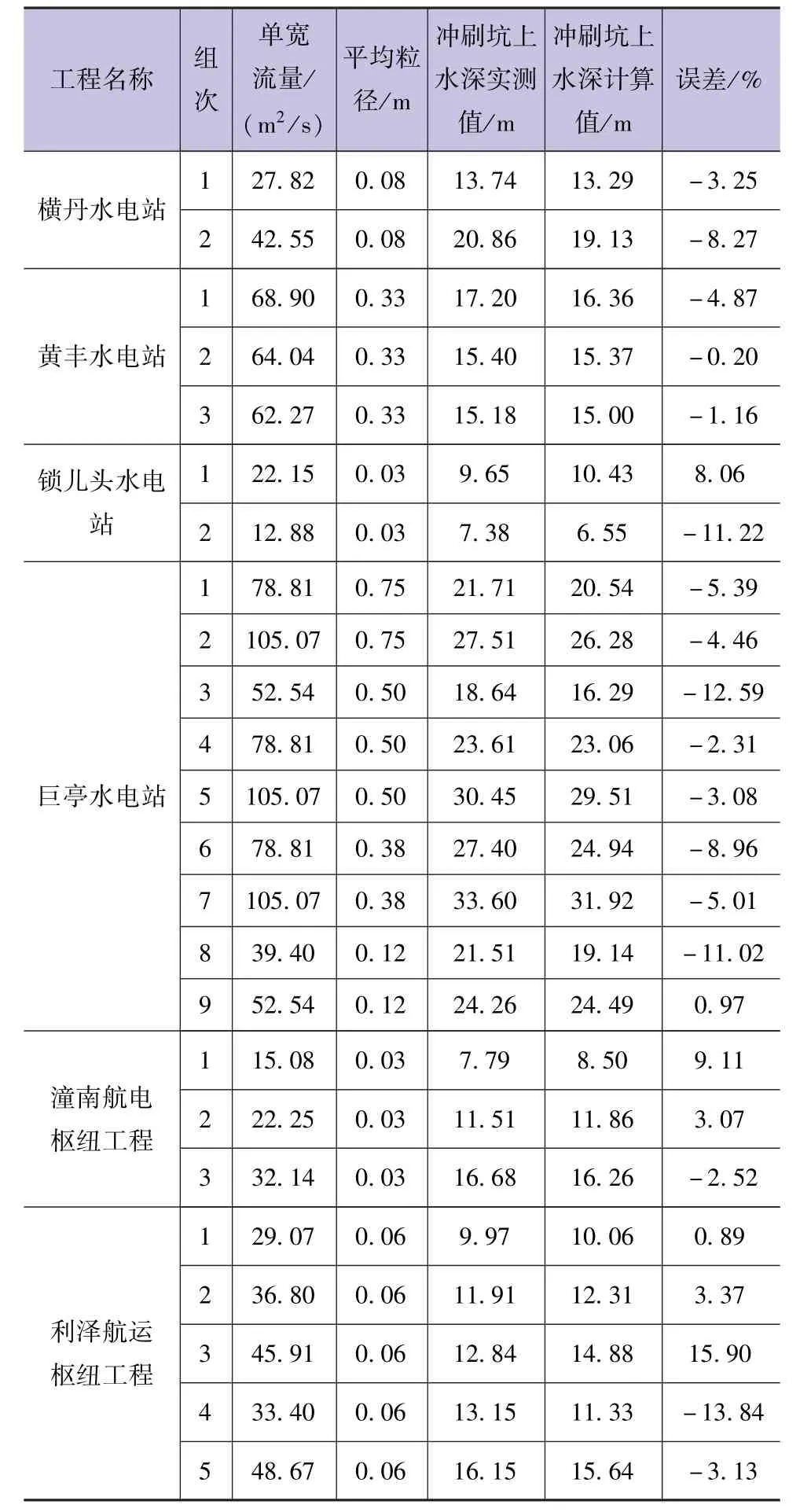
表2 各工程冲刷坑上水深验证结果

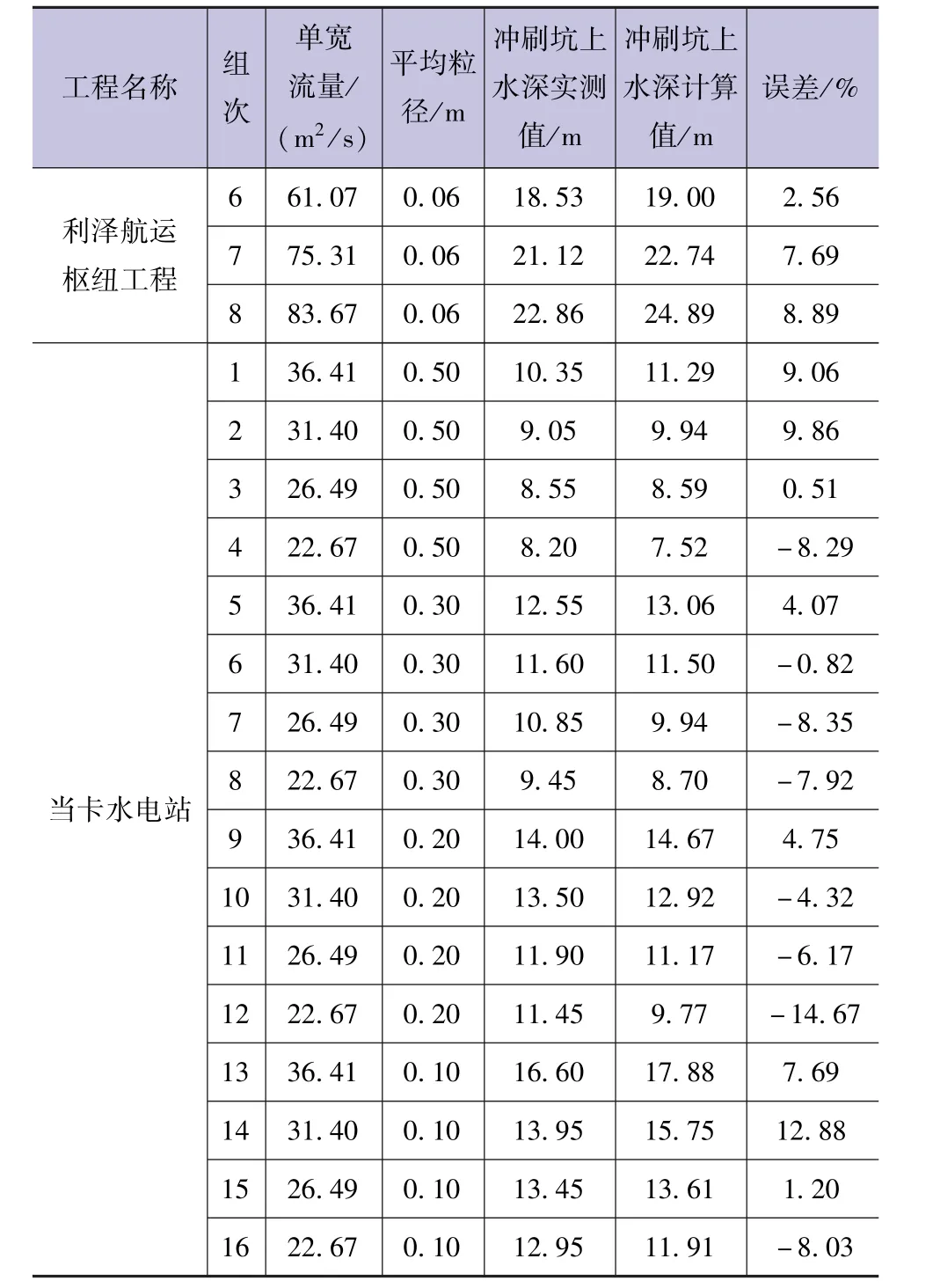
续表

图1 闸坝下游局部冲刷资料验证结果

由图表可见,本文所推导的基于剪切应力下一种新的闸坝下游局部冲刷公式,用多个工程的冲刷资料验证表明,该公式计算冲刷坑上水深值与实测水深值吻合良好,两者平均相对误差在5%以内,表明该公式可以用来预测闸坝下游的局部冲刷深度。

3 结 语

准确预测闸坝式水电站下游局部冲刷坑的深度和形态,可以预判实际工程在运行过程中可能会出现的冲刷问题,提前通过模型试验、数值模拟等手段优化建筑物体型、改变运行工况,有效防止实际工程中因过闸水流的冲刷而形成冲刷坑,有效避免工程因冲刷而造成破坏,从而保证电站和建筑物的安全。本文对目前7类冲刷公式进行了对比研究,分析了各类公式推导所依据的理论、适用条件以及各家公式的优缺点,并在前人研究的基础上推导出了一种闸坝下游局部冲刷的计算公式,该公式表明,闸坝下游局部冲刷深度的主要影响因素为水流的单宽流量和泥沙平均粒径,冲刷深度与单宽流量成正比,与泥沙平均粒径成反比,且单宽流量的影响要大于平均粒径的影响。并选取了其他7个工程的43组冲刷资料进行验证,结果吻合良好。因此,该公式可以用来很好地预测闸坝式工程下游的局部冲刷问题,有效避免因冲刷对电站造成破坏。