几何约束下噪声一致性的图像拼接篡改检测

路东生，张玉金，朱 海，姜月武

(上海工程技术大学 电子电气工程学院，上海 201620)

数字图像是信息交流的重要媒介之一，新闻刊物上的图片、公共场所的监控记录、政治领域的外交影像等均发挥着重要的作用。随着数字图像编辑软件日趋智能化，即便是普通用户也能轻松地对数字图像进行篡改而不留下明显的可视痕迹。复制-粘贴[1-4]和拼接[5-8]是图像篡改中的普遍手段，图片复制-粘贴是在同一张图片中进行的操作，即复制图片中的局部区域并粘贴在同一图片的另一个区域，从而形成伪造图片。此类篡改手段多用于隐藏物体或增加物体数量等。拼接篡改是把来自两张或多张图片中不同的局部区域进行拼接以形成伪造图片。本文主要针对图片拼接篡改检测进行研究。

如前所述，拼接图像由不同的源图像构成。在对图片进行拼接时，通常会引入源图像的一些固有特征[9-11]，例如光电响应[12-13]、噪声特性和光照等。文献[14]计算每个局部图像块的二阶和四阶矩来估计噪声方差，以噪声的一致性作为定位篡改区域的依据。该方法中，将获取的原始信号和噪声峰度值作为噪声估计的基础。但是在实际应用中，噪声峰度值的获取较为困难。文献[15]所提方法的重点则是建立连通区域内自然图像峰度信息和噪声特征之间的关系。此方法同样需要获取原始信号峰度。文献[16]利用小波变换估计图像块的噪声水平，通过设定阈值不断融合领域图像块，最终实现对篡改区域的定位。文献[17]利用带通滤波器下的峰值浓度与噪声水平的关系来判断伪造图像。该方法首先估计每个局部窗口的噪声值，并对其进行K-means聚类，最终确定拼接区域。但是当拼接区域和原始图像噪声差异较小时，该方法的检测结果并不理想。文献[18]利用主成分分析(Principal Component Analysis，PCA)估算每个图像块协方差矩阵的最小特征值，并将其作为图像块的噪声水平，提高了判断准确率。文献[19]在文献[18]的基础上对较大图像块的噪声水平进行估计，从而检测可疑图像块。该研究将较大的图像块继续分割为较小的图形块，并再次进行噪声水平估计，有效地定位了拼接区域。文献[20]使用基于统计的噪声估计方法来计算每个图像块的噪声值并进行聚类。该研究使用由粗到细的策略进行篡改区域定位，当背景区域与拼接区域噪声值差异较小时，篡改区域定位精度仍可保持较高的水平。文献[21]探索了噪声水平函数(Noise Level Function，NLF)与相机响应函数(Camera Response Function，CRF)之间的关系，并拟合了CRF约束下的NLF曲线。该研究通过建立贝叶斯最大后验概率框架对NLF估计性能进行了优化，并利用显著性来区分图片区域。当区域的标准差大于所设置的阈值时，该区域将被认为是拼接区域。

综上所述，基于图像块噪声水平估计的图像篡改检测算法需要对图像块的尺寸进行权衡[19]，较大的图像块可以获得更好的噪声水平估计性能，而较小的图像块则有利于改善定位精度。因此，合适尺寸的图像块是对噪声估计精度与篡改定位精度进行平衡的重要因素。另一方面，当图像块尺寸确定时，准确地定位篡改区域(尤其是篡改区域的边缘)对基于图像块噪声水平估计的图像篡改检测算法也是至关重要的。本文基于早期研究基础，结合拼接图像的纹理信息，提出几何约束下噪声一致性的图像拼接篡改检测方法。该方法不仅能够有效地定位篡改区域及其边缘，还对常规图像的后处理操作具有较好的鲁棒性。

1 图像篡改定位方法

1.1 算法框架

对于待检测图片，首先将其进行分块(分块区域彼此互不重叠)，并评估每个局部图像块的噪声水平。然后，使用K-means算法将图像块聚类为篡改块与非篡改块，形成初步的检测结果并提取其边缘(本文称为篡改块边缘图)。组成篡改块边缘图边缘的点被称为点集合A，以点集合A中非边界点为中心，设置边长为R/2的方形区域，并在边缘图上搜索确定拼接区域的边缘痕迹以组成点集合B。由于点集合B含有大量异常点，故需使用几何约束筛选算法选择正确的点集合并进行连接。最终，确定篡改区域。本文算法的框架图如图1所示。

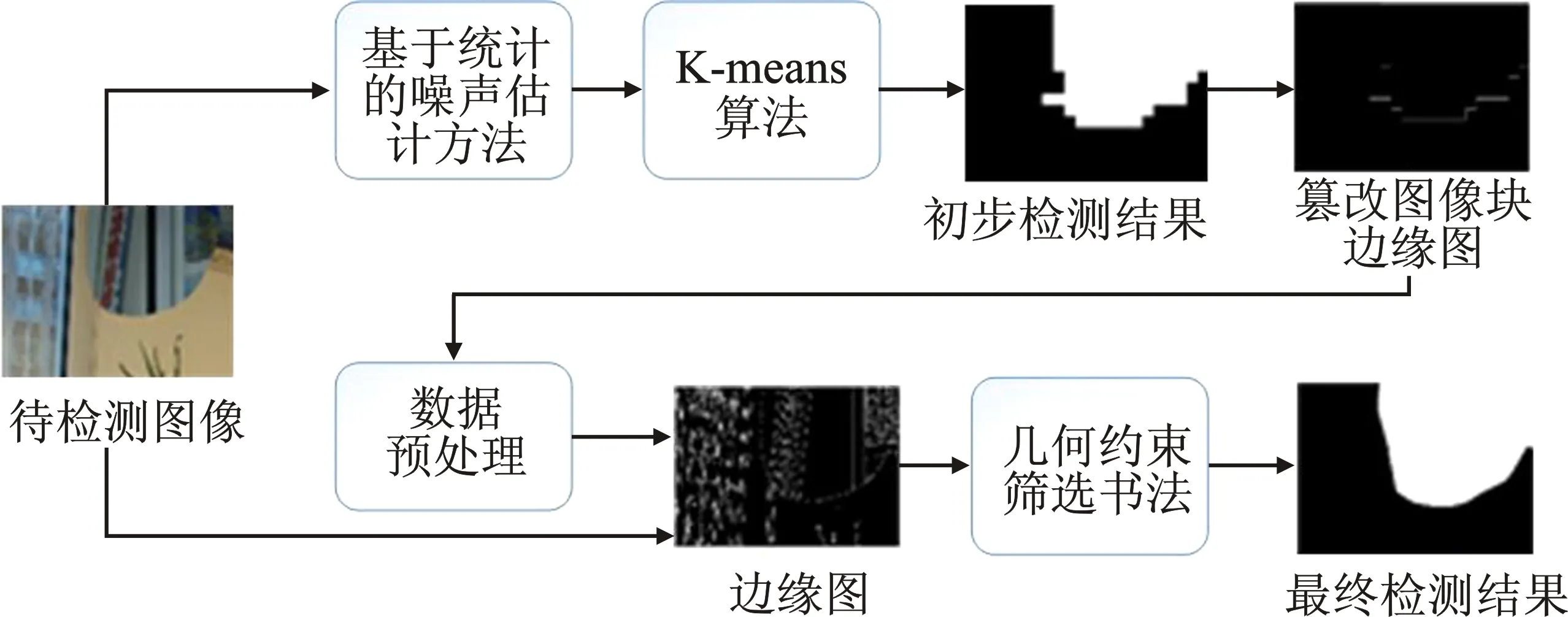
图1 算法框架图

1.2 基于统计的噪声水平估计算法

若将具有不同噪声水平的两张图像拼接为一幅图像，则拼接区域和背景区域将具有不同噪声水平。在数字图像产生的过程中，相机传感器和后处理操作均会引入固有的噪声信息。依据统计特性将噪声分为周期噪声和随机噪声，前者一般来源于图像采集系统中电气和电机引起的干扰，在空间域和频域呈现周期性特点。对周期噪声参数，可采用傅里叶谱进行估计，即当仅有通过传感器的图像可用时，利用恒定灰度值的部分估计概率分布函数的参数。然而在图像拼接过程中，一方面篡改区域会出现“平坦”的区域；另一方面，几何变换、模糊和JPEG压缩等操作均会破坏周期噪声的分布特性，因此本文主要考虑将随机噪声的不一致性作为拼接的线索，随机噪声可以通过对图像加性或乘性操作进行模拟。

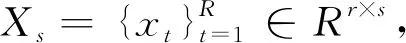
xt=Ayt+et

(1)

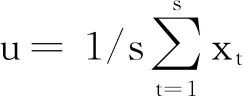
为了精确地定位拼接区域，本文采用由粗到细的两阶段策略[20]。首先将待检测图像分为固定大小的图像块，其维度为2R×2R×3，利用算法1估计图像块噪声水平，并使用K-means算法对图像块噪声水平值进行聚类，将待检测图像分为可疑图像块和非可疑图像块。其中，K-means算法的初值设置如下：首先基于两分类将K设置为2，将估计后的噪声值序列按照从小到大排序。为了在提升聚类效率的同时避免异常点的干扰，将初始值的设置规则设定为：取序列的前1/4长度的数值并取均值作为其中初始值，另外一个初始值被设置为序列后1/4长度的数值的均值；其次将图像块分割为维度为R×R×3的较小的图像块，采用算法1的噪声估计方法来估计每个图像块的噪声水平；最后，向非边缘图像块和边缘图像块赋予不同比例的两阶段噪声估计值，并确定图像块噪声水平值。

算法1 图像噪声水平估计输入: Observed Image I∈RM×N×c,Patch Size d。1. Generating dataset Xs={xt}Rt=1,which contains s=(M-d+1)(N-d+1)patches with size r=cd2 from the image I。2. u=1/s∑st=1 xt and ∑x=1/s(xt-u)(xt-u)T3. Calculating the eigenvalues {λi}ri=1of the covariance matrix ∑x and order λ1≥λ2≥…λr.4. for i=1∶r do5. г=1/(r-i+1)∑vj=iλj6. if τ is the median of set {λj}rj=1 then7. σ=√τ and break8. end if 9. end for 10. 输出: noise level estimation σ。

基于统计的噪声水平估计方法是目前比较出色的算法之一，它对图像纹理的敏感度低，在速度与精度方面具有良好的性能表现，故本文以此作为图像特征提取方法。

1.3 几何约束筛选算法

1.3.1 数据预处理

在待检测图像上使用基于统计的噪声估计和K-means聚类算法，形成初步的篡改检测结果。由于上述噪声水平估计算法以块为单位，故其定位出的篡改区域会形成锯齿状边缘，如图2(c)和图2(g)所示，拼接区域的边缘无法被精准定位。本文对初步结果图进行形态学操作，得到篡改块边缘图，如图2(d)和图2(h)第4列所示。在组成篡改块边缘图中的点为集合A，将点集合A中位于图像边界的点归为点集合A1，其余点归为点集合A2。

图2 初步检测效果图

1.3.2 异常点筛选算法

若待检测图像的尺寸为L×w，初步检测结果图中的方形局部图像块的边长为R。从图3中可以看出，虽然初步检测结果图形成的边缘能够对真实拼接区域边缘进行刻画，但其与真实的拼接区域边缘仍然存在一定的差距。针对该问题，本文给出了一种有效的拼接区域边缘搜索算法：(1)利用Canny算法获取待检测图像的边缘，边缘图能够精确地刻画纹理边缘(包含拼接区域边缘)；(2)以点集合A2中每个点为中心，依次在边缘图上搜索边长为R/2的方形区域中欧式距离最近的非零点，并对该点进行标记，形成点集合B，其能准确地定位拼接区域边缘。图3为边缘图与搜索示意图。

图3 边缘图与搜索示意图

由于拼接区域内部与背景区域的纹理都会在边缘图凸显，是主要的异常点来源之一，基于图像块的噪声估计算法难以区分同时包含拼接区域和背景区域的局部块，造成局部块的漏检与错检，也会导致点集合B存在大量异常点，因此需对点集合B进行筛选，筛选算法如下：

(1)对点集合B进行逆时针排序，利用B集合中每个点与其中心点的反正切值，将散乱无序的点集合B排序，研究其局部特征与整体特征；

(2)基于篡改区域的不规则性与边缘的连续性，依次选取局部连续的5个点的绝对距离与相对距离的离散性作为约束条件

(2)

式中，{LBi|，i=1，…}为点集合B到点cen(点集合B的中心点)的欧式距离

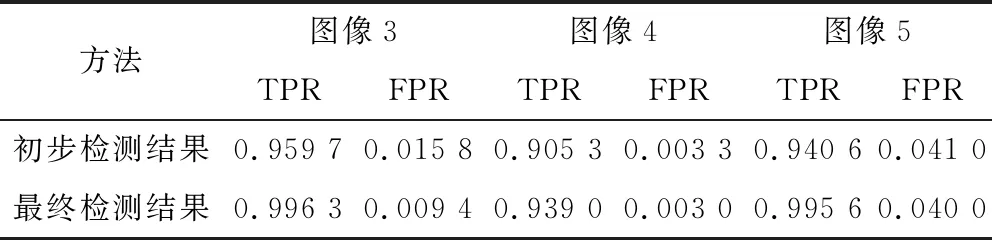
var5(i)

(3)

式中，var5(i)是LBi中连续5个点的方差；mean_var是整体LBi的方差，q为常数

|mean5(j)-uplen|

(4)

式中，q1为常数；uplen是上一个符合式(2)～式(4)的点距cen的距离；mean5(j)为连续5个点距cen的平均距离；

(3)将边界点集合A1与上述条件筛选后的点集合{BBk|k=1，…}合并，结合Alpha-Shape[23]算法将点集合整理为点集合{Cs|s=1，…}并连接形成最终的拼接区域。

算法2 点集合筛选算法输入: Points Set{BBk|k=1,…} Patch Size R, Constant q1,q。1. Calculating the center of {Bi|i=1,…} is cen=mean{Bi}2. angle=artan(dy/dx), dx,dy are difference between ordinate and abscissa of points Bi and cen, order B1≥B2≥…3. LBi =|cen-Bi|2, meanvar=var(LBi), i=1,… mean5(j)=mean(sum(LBi,LBi+1, LBi+2 ,LBi+3 ,LBi+4))4. var5(i)=var(LBi,LBi+1, LBi+2 ,LBi+3 ,LBi+4)5. for p=1:length(Bi)-46. if |LBp-LBp+1|>R/2 || var5(q)>q×mean_var7. continue8. end if 9. if |mean5(p)-uplen|

2 结果与分析

2.1 实验设置

本文的实验环境为装有Windows10系统的台式电脑和MATLAB 2018仿真软件。本文使用哥伦比亚大学未压缩彩色图像库DVMM[24]进行测试实验，所使用的数据集中含有拼接图像和真实图像共363幅，其中183幅是来自不同数码相机拍摄的真实图像，另外180幅为拼接而成的图像，图像格式均为TIFF格式，尺寸大小范围757～568像素至1152～768像素，这些图像主要在室内拍摄而成，场景包含走廊、办公桌、人物、盆栽植物等。

为评估本文方法的有效性，使用正确检测率(True Positive Rate，TPR)和错误检测率(False Positive Rate，FPR)进行评估，计算式为

(5)

(6)

式中，FN表示篡改像素点被误检测为真实像素点的数量；FP表示真实像素点被误检测为篡改像素点的数量；TN表示真实像素点被正确检测出的数量；TP表示篡改像素点被正确检测出的数量。

2.2 实验结果

2.2.1 几何约束筛选算法定位效果

为了验证几何约束筛选算法的有效性，本文随机从哥伦比亚大学未压缩彩色图像库DVMM中抽取3幅拼接图像，将其编号为图像3、图像4和图像5，用于对比几何约束筛选算法的效果。图4所示的是应用几何筛选算法前后的对比图，实验所用图像来自于哥伦比亚大学未压缩彩色图像库DVM或使用Photoshop在flickr.com网站上拼接获得。

由图4可知，图4的第3行为初步检测mask图。初步检测图存在锯齿状分割结果，其与真实拼接区域边缘存在一定差距，拼接区域边缘信息保留较少。经过搜索拼接痕迹可以找到拼接区域的大致边缘点集合A2，如图4第4行亮白色标记点所示。此外，A2中包含不属于拼接区域边缘的点集合，这些来源于拼接区域内部或者背景区域的点被称为异常点。

由于拼接区域具有不规则的特点，因此去除异常点需要考虑拼接边缘的局部性与整体性。几何约束筛选算法利用相对距离的整体离散性与局部连续点筛选异常点。图4的第4行、第5行分别是未处理和应用几何约束筛选算法后的结果，由图可知，采用几何约束筛选算法能够有效筛选点集合。本文以5个连续点来考虑局部性，利用式(2)能够有效限制点位置的剧烈突变，而采用式(3)则可将局部点的离散程度与整体离散进行关联，从而判断局部点相对整体点集合的合理性。式(4)用于进一步判断点的规范性。最后，采用Alpha-Shape算法对点集合取得最小多边形边界来定位拼接区域，如图4中第6行最终检测结果所示。

图4 应用几何筛选算法前后对比图

对图像3～图像5应用几何约束筛选算法前后的正确检测率与错误检测率结果如表1所示。由表1可知应用几何约束算法可增加正确检测率，降低错误检测率。对应于图4第6行，几何约束筛选算法可有效去除初步检测结果图中被误检测的背景区域，增加漏检的篡改区域，消除图像块形成的锯齿状，实现更精确的拼接区域定位。

表1 应用几何约束筛选算法性能指标对比

2.2.2 移植几何约束筛选算法性能比较

由于几何约束筛选算法具有较好的可移植性，为了验证对基于图像块噪声水平估计算法性能改善的有效性，本文随机选取3张哥伦比亚大学未压缩彩色图像库DVM中的拼接图像(将其编号为图像6、图像7、图像8)，分别在文献[16]、文献[19]和前期方法[20]的检测结果图上增加几何约束筛选算法处理操作。本文中，将进一步的检测结果记作[16]-GCF、[19]-GCF以及本文的方法结果，如图5所示。

图5第1行分别是拼接图像6～图像8。图5的第3行和第5行分别是文献[16]与文献[19]中算法篡改区域的定位结果。由于背景和拼接区域内部纹理影响以及噪声差异较小，因此采用文献[16]、文献[19]中的方法所获得的定位效果较差，这两种算法无法完整定位篡改区域，导致出现拼接区域内部以及边缘部分漏检和背景区域误检的情况，定位边缘不连续，凹凸也不一致。图5第4行和第6行分别是在文献[16]和文献[19]方法基础上应用几何约束筛选算法的实验结果。由图可知，在应用几何约束筛选算法后，拼接图片的篡改区域的定位更加准确，保留了更多的边缘信息。由图5第7行可以看出，本文方法相较于文献[16]和文献[19]方法具有较强的噪声提取能力，可对拼接区域边缘进行更加细致的区分。

表2是对图5结果的定量分析。文献[16]和文献[19]中的方法分别对应图5中第3行与第5行检测结果的定位分析。[16]-GCF、[19]-GCF对应图5的第4行与第6行，分别代表在文献[16]、文献[19]方法上结合应用几何约束筛选算法后的检测结果。文献[16]中的方法通过结合几何约束筛选算法后，图像6～图像8的平均正确检测率提高了约15.9%，错误检测率降低约2.9%。文献[19]中的方法结合几何约束筛选算法后，图像6、图像7和图像8的平均正确检测率提高约18.8%，错误检测率减少约2.6%。综上所述，将原有方法结合几何约束筛选算法后，能够提高以块为单位的噪声水平估计算法的准确率，保留更多拼接区域的边缘信息。上述结果也表明几何约束筛选算法具有良好的移植性。

图5 移植几何约束筛选算法效果图

表2 移植几何约束筛选算法性能指标对比

2.2 算法鲁棒性分析

JPEG图像压缩、几何变换和拼接边缘模糊为常见的拼接图像后处理操作。为了进一步评估本文提出方法的鲁棒性，从哥伦比亚大学未压缩彩色图像库DVMM中随机选取一张原始拼接图片，使其分别经过压缩因子QF=95的JPEG压缩及下采样20%操作。后处理操作中，图像拼接部分所加噪声标准差为5。图6为不同后处理图像的定位结果。

从图6篡改区域定位结果可知，原始图像经过JPEG压缩后，会出现部分区域漏检，原因是噪声估计算法性能一定程度上受到JPEG块效应的影响。原始图像经过下采样后，采用本文方法可有效地定位出篡改区域，保留更多的边缘信息，避免出现误检区域。

图6 常见后处理操作结果比较

表3为哥伦比亚大学未压缩彩色图像库DVMM经过后处理操作前后的算法性能对比结果，其中TPR和FPR分别表示180幅拼接图像的平均正确检测率和错误检测率。对比现有文献算法，以文献[16]和文献[19]中的算法为例，两种算法结合几何筛选算法后被记为[16]-GCF、[19]-GCF。从表3中可知，当噪声水平差异较小时，基于噪声水平估计的拼接检测定位方法无法取得理想篡改检测效果。

如表3所示，针对未经过后处理操作的伪造图像，本文所提方法的正确检测率高于采用文献[16～17]及文献[19～20]中的方法，与文献[21]所提方法接近，但文献[21]中方法的错误检测率高于本文约12.7%；在文献[16]和文献[19]方法的基础上应用几何约束筛选算法处理后，正确检测率提高了2%～7%，错误检测率降低1%～2%，其中[19]-GCF相对于文献[16]所提方法的正确检测率提高了约7.8%，而[16]-GCF正确检测率则比文献[16]中的方法提高了约1.6%。其原因在于文献[16]方法的检测结果多数偏离真实拼接区域的边缘。在文献[19]基础上，采用改进的[19]-GCF方法可取得较高的性能提升，表明本文方法在一定程度上能够有效地定位篡改区域，结合几何约束筛选算法后的综合性能也优于现有方法。

通过表3可知，本文方法在检测JPEG压缩方面表现较差，结合几何约束筛选算法后性能略有下降，方法[19]-GCF的正确检测率和错误检测率均低于文献[19]中的方法。但本文方法对于后处理下采样20%表现较好，其正确检测率均高于文献[16～17]、文献[19～21]中的方法。本文方法的正确检测率高于文献[21]中方法约13.5%，错误检测率减少约11.5%，保持较低水平。[16]-GCF与[19]-GCF的正确检测率平均提高了约4%，错误检测率并未明显增加。由此可知，本文所提出的拼接检测方法对常见后处理操作具有鲁棒性。

2.3 时间复杂度

为了评估本文方法的时间复杂度，表4给出了同一环境下不同算法的检测时间。这些被比较的算法包括本文所提的方法、文献[16]所提方法、[16]-GCF、文献[17]所提方法、文献[19] 所提方法、[19]-GCF、文献[20] 所提方法和文献[21]的方法。每幅图的平均时间包括读取图像、噪声估计和拼接区域定位的时间。

表4 图像拼接定位方法运行时间比较

由表可知，文献[16]和文献[20]所提算法的复杂度较低，所用时间最短。本文方法增加了纹理信息处理阶段，并增加了时间复杂度以获得较高的拼接图片定位精度。

3 结束语

本文提出了一种几何约束下噪声一致性的图像拼接篡改检测方法。该方法在对拼接图像分块的基础上使用基于统计噪声估计算法对噪声水平进行估计，将噪声值聚类定位初步篡改区域，根据噪声值定位初步篡改区域并提取篡改区域的边缘点集合。在拼接图像的边缘图像上以点集合为中心，在方形区域内搜索拼接区域边缘点。对于图像中拼接区域和背景区域中纹理产生的异常数据，采用几何约束筛选算法筛选正确的拼接区域边缘点集合，消除了锯齿状边缘对篡改区域的影响，并且几何约束筛选算法可被成功地应用在其它基于块的噪声水平评估方法中。在实验中，本文提出方法的性能优于现有方法，原因是本文所提出方法在利用噪声一致性的同时结合了拼接区域边缘，对拼接区域与背景区域进行了区分，因此对常见的图像处理具有一定的鲁棒性。本文方法为图像篡改被动取证的精准定位提供了一种新思路，今后的工作将继续加强算法的鲁棒性，以便应对更复杂的图像篡改情况。