基于深度学习的量子信号大气衰减系数预测

李天秀,石磊,王俊辉,李佳豪

(空军工程大学信息与导航学院,陕西 西安 710077)

0 引言

基于量子力学基本原理的量子通信技术以其理论上的无条件安全性[1,2]成为保密通信领域的热点之一。目前,量子通信技术已进入实用化乃至全球网络化建设的进程,在远距离量子通信过程中,自由空间量子通信系统具有损耗小、灵活性强、传输距离远等优点,是全球化组网的重要方式[3-5]。在自由空间量子通信过程中,量子信号会受到复杂大气环境的影响,从而不可避免地出现量子信号的衰减,对量子信号大气衰减情况的分析研究是提高自由空间量子通信性能的重要理论基础之一。

在理论模型研究方面,Nie等多个团队[6-8]研究了包括雾霾、雷暴云在内的多种大气环境对量子信号在空间中远距离传输的性能的影响。Vasylyev等[9]针对雨、雾天气下量子光信号经过大气湍流后的性能变化建立了近似椭圆光束的量子光模型。上述研究在对量子信号空间信道特性建模分析的基础上提出了相应的补偿方案以应对大气环境影响,而补偿方案的实现和优化是进一步研究的重点。

2019年,南京邮电大学王琴团队提出了一种使用深度学习方法进行主动预测和反馈控制的相位漂移解决方法[10]。该方案利用长短时记忆网络结合实时获取的温度、湿度、光强等数据对相电压进行预测,并根据预测结果进行参数预调整,有效提高了系统传输效率,并降低了系统误码率。该方法的核心思想是利用深度学习方法,在可实时获取的参数基础上对关键参数进行预测,并根据预测结果预先使用相应的补偿方案,最终实现系统参数的动态调整和性能的实时提升,在空间量子通信系统中同样也可以应用这一思路。

在空间量子通信系统中,大气条件的改变会影响最终密钥率的生成。针对不同大气信道条件,对包括信号光强度在内的各种系统参数进行有效调整和选择,可以优化系统最终的密钥生成。大气信道参数是其他参数调整的基础,对大气信道条件的预测为预先的参数调整提供了依据,使得光源等系统参数的调整可以有针对性地预先进行,以获得实时优化效果。

本文基于上述研究思路,采用深度学习方式,利用可获取的气象数据提出了量子大气衰减系数的预测方案。分别利用误差反向传播神经网络(BPNN)、长短期记忆网络(LSTM)、门限循环单元(GRU)三种神经网络模型,并根据测试情况对网络性能进行了分析比较。这一方案能够为针对时变大气信道的补偿方法提供数据基础,同时可以根据不同系统的实测数据进行更深入的探索和拓展。

1 方法与数据

1.1 实验流程

本量子信号大气衰减系数预测实验的具体流程如图1所示,包括数据预处理、模型构建与训练数据预测与分析。各步骤具体内容如下:

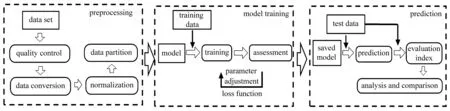
图1 实验流程图Fig.1 Flow chart of the experiment

1)数据采集与预处理。数据的预处理主要包括数据质量的控制、数据转化、归一化处理、数据集的划分。数据质量的控制包括去除坏点和数据补缺;数据转化、归一化处理及数据集的划分将在后文进行详细说明。

2)模型构建与训练。分别使用BPNN、LSTM、GRU三种深度学习算法进行模型构建,以及算法初始参数设置,并根据训练情况进行参数调节。

3)数据预测与分析。将测试集数据输入不同网络模型中,输出预测结果。对预测结果和实测值进行数学分析和比较。

1.2 量子信号大气衰减系数与大气能见度

量子光信号在大气信道内传输的过程中会受到包括大气分子吸收、悬浮微粒吸收、瑞利散射、米氏散射在内的多种因素影响[11],导致光信号强度的衰减。定义光信号经过大气信道前后的强度比值为大气信道传输效率ηatm,其与大气环境和传输距离的关系可以表示为[12]

式中:α为大气信道衰减系数,用于表征大气环境对量子信号衰减的强弱;L表示传输距离。α在实际条件下可以通过实验数据获得,为了便于估测,文献[13]根据实验结果进行拟合,给出了大气信道衰减系数与能见度之间的经验公式

式中:γ表示通信过程使用的信号光波长,Vν为能见度,参数q的取值与能见度的关系为

本研究利用(2)、(3)式对能见度数据进行转化,从而获得大气信道衰减系数的原始数据,作为输入向量的重要参数之一。

1.3 数据预处理

本实验所使用的数据集为西安地区气象数据,气象站区站编号57036,位置为北纬108.93°,东经34.3°,数据集记录了2018年6月至2020年6月的气象数据,包含气压、温度、相对湿度、风速、能见度数据,数据采样间隔为3 h,数据样例如表1所示,衰减系数由能见度通过(2)、(3)式转化得到,其中通信波长取值为850 nm,气温、气压、湿度、风速数据均为平均值。

表1 数据样例Table 1 Samples of raw data

由于不同变量采用不同单位,为了便于不同输入变量的复合计算及模型训练,需对输入数据进行归一化处理,即

从而使其映射在[0,1]范围内,其中x*表示归一化后的数据,x为原始数据,xmin和xmax分别表示相应数据集合内的最小值和最大值。

经预处理和整理后得到的数据集共6000条,将其划分为30个数据集合,每个数据集包含200条数据。数据集按9:1的比例划分训练集和测试集,即27个数据集共5400条数据用于模型训练,三个数据集共600条数据用于模型测试。在不同网络结构中使用的数据集及划分方法相同。

2 网络模型与构建

2.1 反向误差传播神经网络（BPNN）

1986年,Rumelhart等[14]提出反向误差传播(BP)学习算法。该算法利用输出后的误差来估计输出层的直接前导层误差,再以此估计更前一层的误差,如此反复可获得各层的误差估计。采用BP学习算法的前馈型神经网络即BP神经网络(BPNN),其基本结构如图2所示。BPNN是具有很强非线性映射能力的柔性网络结构,网络中包含输入层、隐藏层、输出层,中间层数和各层的神经元个数可根据模型的需要和网络训练情况进行调整。BP神经网络的训练过程包含工作信号正向传播运算和误差信号通过传播反馈调节网络两个部分,这两个过程交替迭代进行以完成网络功能。

图2 BPNN结构图Fig.2 Structure of BPNN

BPNN典型网络结构如图2所示。正向传播时,样本数据由输入层传入,经隐藏层逐层处理后流向输出层。在输出层判断实际输出与期望输出的关系,若取值不符,则进入误差的反向传播环节。反向传播时,将输出通过隐藏层向输入层逐层反向传输,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,依据误差信号对权值进行修正。网络权值修正的过程可使最终的实际输出值向期望值无限接近,直至满足预定精度。

本研究使用的BPNN网络采用经典三层网络结构。输入层的输入向量包含四个气象数据值及大气信道衰减系数值;隐藏层采用单层结构,层内含有30个神经元;输出层为单一输出,学习率参数设置为adaptive模式。

2.2 长短时记忆网络(LSTM)

1997年Hochreiter和Schmidhuber[15]提出的长短时记忆网络(LSTM)是循环神经网络(RNN)的一种改进类型,适用于时序数据的分类、处理、预测。LSTM网络的外部结构与传统RNN结构相同,但其隐藏层的改变可以有效解决RNN网络训练时可能会出现的梯度消失、梯度爆炸等问题,LSTM结构如图3所示。

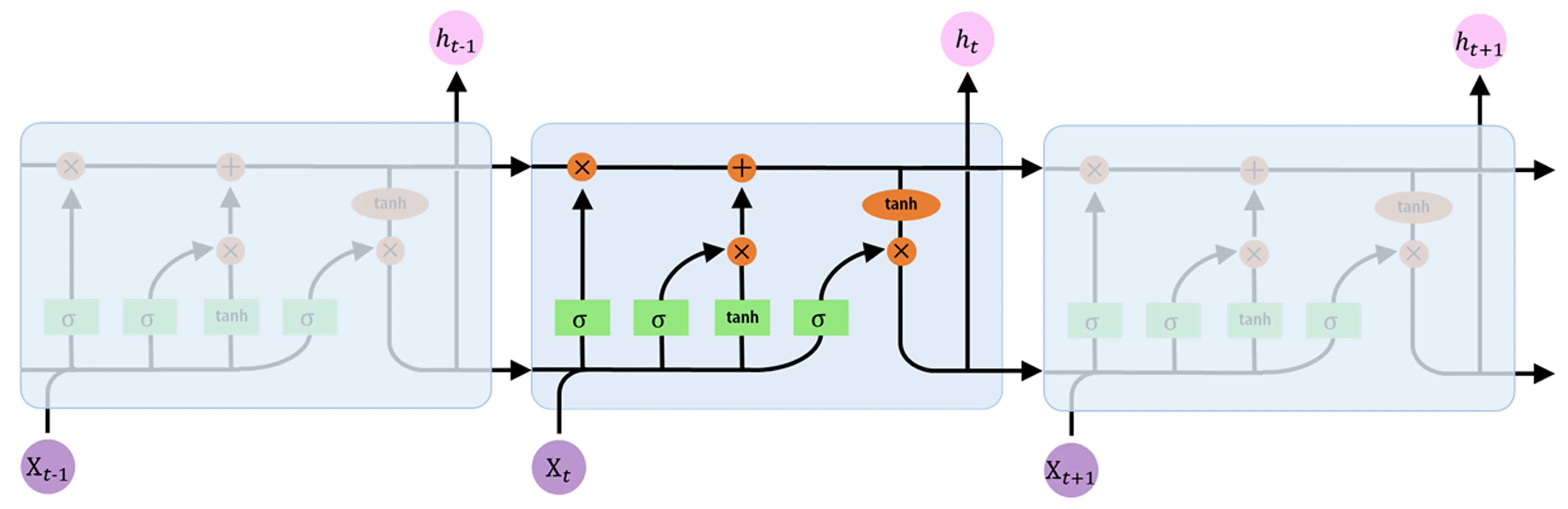
图3 LSTM结构图Fig.3 Structure of LSTM

典型的LSTM网络单元包含输入门、输出门、遗忘门。其中遗忘门会根据当前时刻输入和上一时刻输出决定记忆数据中的哪一部分需要被丢弃,这一环节是LSTM与传统RNN网络的重要区别;输入门根据当前时刻输入和上一时刻输出对上一时刻单元状态进行数据更新,形成新的单元状态;输出门则根据最新单元状态、上一时刻输出和当前时刻输入决定该时刻输出值。具体公式推导过程参见文献[16]。

本文选择的LSTM网络模型包含双层LSTM网络,每层含有100个神经元,采用均方误差作为损失函数、tanh函数为激活函数并在每层后加入Dropout层,从而防止数据过拟合。

2.3 门限循环单元(GRU)

作为LSTM最为成功的变体之一,GRU网络是在LSTM基础上进行简化得到的,其保留了与LSTM相近的效果,GRU基本网络结构如图4所示[17]。GRU网络单元将LSTM网络单元的三个门整合为两个门,使用重置门控制前序隐藏状态的保留,实现了LSTM中遗忘门和输入门的信息控制。

图4 GRU结构图Fig.4 Structure of GRU

本实验中GRU网络使用Keras框架下RNN模块中的GRU类,初始化定义隐藏层数为256,使用adam优化器,并同样添加Dropout层以防止数据过拟合,数据输入输出格式与BPNN网络相同。

3 评估与讨论

3.1 评价指标

为了有效衡量模型的预测性能,本研究采用拟合度(R2)、均方根误差(ERMS)、平均绝对误差(EMA)三个指标作为性能评价指标。各评价指标的具体定义为

式中:yi为实际数据值,为数据集实际数据平均值,为预测数据值。

上述指标中R2表征自变量与因变量之间的整体拟合度,数值越接近1,说明预测值与实际值拟合程度越高,模型性能越好。ERMS能够反映测量的精密度,EMA表征数据的离散程度,上述两个指标数值越小,则模型的整体性能越好。

3.2 结果分析

利用前文预处理后的数据和网络模型分别进行训练可以得到最终预测网络,采用单步预测方法并利用测试集数据进行预测,分别计算三种预测网络的评价指标,用以比较分析。

图5所示为三种预测网络预测结果与测试集实际数据分布的散点密度图,图中数据为归一化后的数据,预测数据未进行数据还原。需要说明的是真实的原始数据存在如图6所示的峰值,且峰值处数据变化显著,即此时大气条件显著恶化,通信性能严重衰减。为了保证实验数据的真实性和实验结果对现实情况的有效表征,未对这部分数据进行剔除,导致大部分数据处于相对低位,这也是图5中散点主要集中于低位的原因。从散点图分布及密度来看,BPNN网络在数据处于相对平稳的低取值时预测性能良好,但部分数据存在明显偏离。LSTM和GRU网络预测结果整体分布较好。LSTM网络在个别尖峰数据点时存在较大误差,GRU网络出现了个别极大偏差数据,该数据点将会对性能指标的评价产生较大影响。

图5 预测值与真实值的散点密度。(a)BPNN;(b)LSTM;(c)GURFig.5 Scatter diagram of predictive and actual values.(a)BPNN;(b)LSTM;(c)GUR

根据图6中对单组数据的预测数据和实际数据折线图的比对可以发现,三种网络预测结果的趋势与实际数据趋势基本相似,BPNN网络在低取值部分的数据拟合程度较好,但在峰值处存在明显误差;LSTM网络在低取值部分数据相对误差较大,但由于数据值本身较小,因此绝对误差较小,整体拟合度较高;GUR网络对于峰值处数据的预测能力明显较好,使得整体网络性能表现更佳。

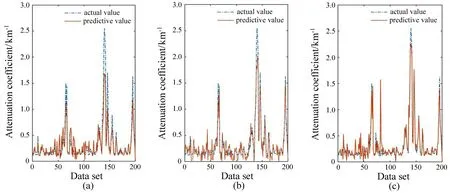
图6 预测值与真实值曲线拟合。(a)BPNN;(b)LSTM;(c)GURFig.6 Fitting of predictive and actual values.(a)BPNN;(b)LSTM;(c)GUR

表2中给出了三种网络模型评价指标的计算结果,其中R2与散点图中数据密度及数据分布结果一致,BPNN网络的预测性能与LSTM和GRU网络相比相对较差,但是仍然能够实现80%以上的数据拟合度。就ERMS和EMA两个指标来看,BPNN网络的整体性能也相对较差,LSTM和GRU网络性能基本相同,其中GRU网络的ERMS较大,很大程度上受到了个别离散数据点的影响,若对存在极大偏离的数据点进行修正,则GRU网络的整体性能都将稍优于LSTM网络。

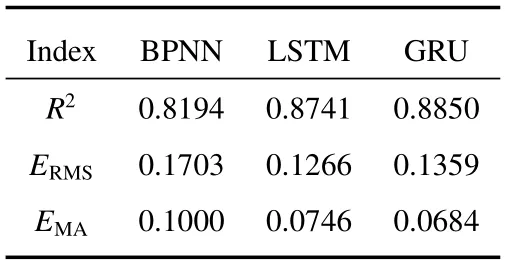
表2 预测网络性能指标Table 2 Evaluation results of prediction network

综合数据分布和评价指标可知,三种网络结构均能实现量子信号大气衰减系数的有效预测,且均能够获得80%以上的数据拟合,LSTM及GRU网络具有整体更为良好的性能。在大气条件相对稳定的情况下,即数值处于相对平稳的低位时可使用BPNN网络作为预测手段。对于急剧变化的数据点,BPNN预测误差虽然较大,但是仍能对突变情况起到预警作用。当大气条件处在波动相对较大的情况下时,应考虑使用GUR网络,同时需要通过进一步的训练避免个别极大偏差数据的出现,以获得更好性能。

三种网络模型的预测能力均需要进一步优化,特别是对部分偏离数据和尖峰值的预测能力需要明显改善,从而获得更佳的预测结果。同时可以在优化数据集、提高时间密度的基础上采用多步预测方法,从而更好地表征信道变化过程的时间连续性。

所提出方案可以为通信系统优化提供数据支持,这里以诱骗态MDI-QKD量子通信系统光源优化为例进行简介。根据仿真分析及相关实验,信号态、诱骗态光强的设置对诱骗态MDI-QKD系统的密钥生成有一定影响,在一定条件下存在最优化的光源选择方案[18,19]。在光纤信道中,一般认为影响光源强度选择的重要因素是信道长度,其本质上影响的是通信链路的衰减,因此在空间通信系统中对大气信道衰减系数进行预测,结合空间信道长度可以有效预估空间信道衰减,并有针对性地对信号态、诱骗态光强进行调整,从而实现系统的实时优化。

4 结论

在大气信道条件实时变化的背景下,针对量子信号大气衰减系数实时变化情况提出了基于深度学习的预测方式,分别使用BPNN、LSTM、GRU三种深度学习算法进行了实验验证。对三种深度学习网络的训练和测试证明了利用深度学习方法预测量子信号大气衰减系数方案的可行性和有效性,同时通过对比可以发现:BPNN网络性能相对较差,LSTM和GRU具有更好表现,拟合度可以达87%以上。依据实验结果,在后续实践应用中可以选择LSTM或GRU网络进行数据预测,并进行进一步的数据集和网络优化。本研究所提出的预测方法和实验结果为包括光源参数等系统参数的预先优化调整提供了数据支持,将针对给定信道条件的优化方案有效拓展为实时、动态的优化方案,为后续工程化应用打下了基础。