一种风力发电系统输出功率波动抑制策略研究
徐茂栋,许媛媛,朱少欣,贾宪章
广东海洋大学,广东湛江,524000
0 引言
随着传统能源的日益枯竭和由此带来的环境问题,环保、清洁的可再生能源成为世界各国研发的热点,作为清洁可再生能源之一的风能得到了快速发展,风力发电已成为电力系统的重要组成部分[1]。但风场的不确定性和间歇性会引起发电机输出功率的波动,引起电网的冲击,降低电网电能质量,增加发电系统并网技术的难度。基于储能装置可以实现风电系统固有波动的抑制,使风电这种间歇性、波动性很强的可再生能源变得“可控、可调”,使电网对这种最接近规模化发展的能源调度变为可能。因此,本文提出一种基于一阶低通滤波器的储能系统优化控制策略,该控制策略可实现风电机组功率波动的平滑控制,优化配置储能系统容量,并通过建模仿真验证该控制策略对风电系统能有效抑制输出有功功率的波动[2]。
1 风电能源管理系统拓扑结构
风场的高随机性导致风电间歇式电源输出功率的高波动性。储能系统是实现微电网协调优化运行、减少弃风现象及提高能源利用率的一个重要环节。因此,需要提出一种合理的储能系统控制策略,来平抑可再生能源的功率波动[3],提高系统的可靠性和效率,以维持微电网的稳定性和经济性。目前比较常见的几种储能系统包括:储能系统并联于直流侧拓扑结构、超级电容单独在直流侧并联拓扑结构、蓄电池单独在直流侧并联拓扑结构等。在此基础上,本课题提出了一种改进后的储能系统拓扑结构,如图1所示。

图1 储能系统拓扑结构
图1中的风能发电通过风能带动风力机的叶轮旋转,将风能转换为机械能,再通过齿轮箱将叶轮较低的转速转换为发电机较高的转速,最后由发电机将动能转换为电能并通过AC/DC变换器与直流母线相连[4]。蓄电池由 DC/DC2 变换器与超级电容连接,构成混合储能单元,再通过DC/DC1变换器与直流母线连接,鉴于超级电容的高功率密度,可以快速地发出较多的能量。在本文研究的结构中,超级电容器通过DC/DC1变换器连接于直流母线,由超级电容吸收和释放能量对母线功率不稳定的高频分量进行抑制。采用相应的控制策略能较好地控制蓄电池和超级电容的出力,蓄电池作为能量型储能元件主要承担微网中波动功率的低频部分。本文所研究的结构中的两个变换器可以分别运行,互不干扰,提高了充放电的效率,可快速稳定波动,并能减少蓄电池的循环次数,延长蓄电池的生命周期。
2 风电系统输出功率波动的抑制策略
风场的随机性和间歇性引起风电系统输出功率的高波动性,不仅增加了电网的冲击,还会降低电能质量,导致微电网的稳定控制变得困难。为了减小风电场输出功率的波动,提出一种基于混合储能系统的一阶滤波算法功率分配策略,对风电场输出功率波动进行平抑控制[5]。通常并网功率参考值由风电机组发出的有功功率经一阶低通滤波器得到,即:

式中,Pw是风电场的输出,Pb是平滑后的总输出,Ts是时间常数。
图2是一种定常数低通滤波拓扑结构,通过一阶定常数低通滤波器对风电机组输出功率的波动进行平抑[6],储能系统对部分控制系统的输出功率进行平抑,维持电网稳定。储能系统包括储能单元和功率变换单元两部分,其通过功率变换单元向交流母线注入或抽取能量来平抑风电场输出功率Pb,改善风电并网情况。

图2 定常数低通滤波拓扑结构图
图3是一种定常数低通滤波的算法流程图。首先,输入风电功率Pw,通过选取不同时间常数T的一阶低通滤波器进行平滑控制后得到风电功率Pb。其次,计算不同时间常数T控制下的风电输出功率的波动率,并对波动率小于2%的风电功率进行统计。最后,对不同的统计图进行比较分析,选取最优时间常数T,进而确定储存容量和最大风电功率。
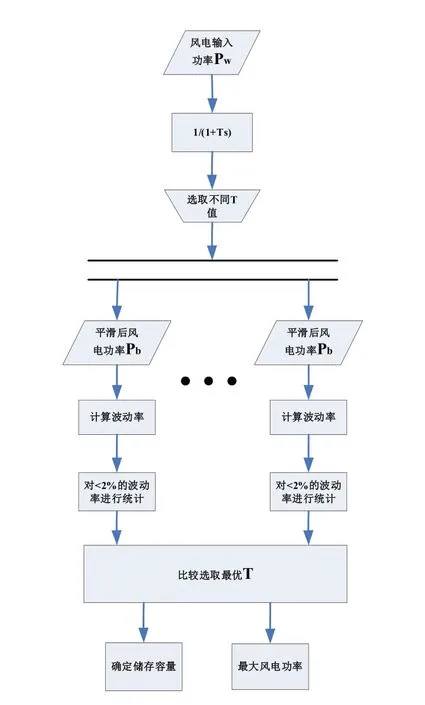
图3 定常数低通滤波的算法流程图
3 建模仿真
基于有限元分析软件搭建风力发电系统计算模型,对风电系统输出功率进行仿真分析。仿真结果如图4所示,波动率超过2%的占到一半以上,从目前现有研究参考,本文设定波动率2%为设定参考值。在80分钟时所采集的数据中可以得出,超过2%的波动率占到了一半以上,故需要加入滤波器进行功率平滑。
(1)未加入滤波器时的输出功率波动率情况。未加入滤波器时的输出功率波动率情况如图4所示。

图4 原始数据风电机组每分钟波动情况
(2)加入滤波器时的输出功率波动率情况。为抑制风电场输出功率的波动,在上述建模的基础上增加了一阶滤波器环节,计算分析了不同时间常数对功率波动率的影响,并由此选出对输出功率波动的抑制最佳的时间常数T。
由图5和图6可知滤波器时间常数为T=400s时波动率限制在2%以内的比例已经占到了80%以上;时间常数为T=800s时波动率低于1%的波动率已经占到了80%,低于2%的波动率占到了95%左右,平滑作用较明显。时间常数为T=1000s时满足了波动率在低于2%范围之内的要求,平滑效果明显。时间常数为T=1200s时波动率小于2%的概率已经接近于99%,平滑效果比T=1000时效果要好。

图5 各时间参数下风电功率平滑效果

图6 各时间参数下风电机组每分钟波动情况
T越大,实现滤波器的成本越高,详见表1。T=1000s时的最大波动率为1.99%,T=1200s时的最大波动率为1.74%。综合考虑现有研究成果得出,T=1000s既满足了平滑性的需要,又降低了成本。当T=1200s时波动率小于2%的概率已经接近于99%,平滑效果比T=1000s时效果要好。同时,表1中不同时间常数的平滑效果对比也说明了随着T的增加,最大储能容量和最大储能功率也在增加。

表1 不同时间常数的平滑效果对比
时间常数与系统的储能容量和储能功率都有着密切的关系,通过在不同时间常数分别对储能容量和储能功率的影响作对比,可以说明时间常数T对储能功率和储能容量的作用,图7和图8比较直观地说明了T越大,储能功率和储能容量也会随之加大。
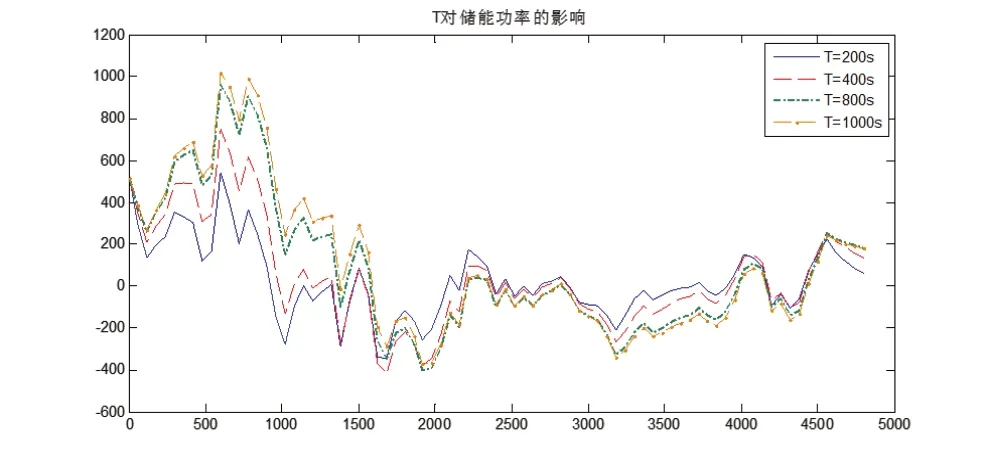
图7 时间常数T对储能容量的影响

图8 时间常数T对储能功率的影响
微电网对风电功率有不同的要求时,所需要的储能容量配置也不一样。由表2中不同波动率所需参数对比得出,在不同的最大波动率限幅下,所需要的储能系统配置要求差别也比较大。

表2 不同波动率所需参数对比
通过仿真结果可知,采用一阶低通滤波器对风电输出功率的波动具有很好的平抑作用。通过调整时间参数,利用统计学原理,综合得出滤波效果的性能指标,使波动率满足低于2%的目标。
4 结论
针对风力发电系统输出功率波动的问题,本文提出了一种定常数低通滤波拓扑结构,在此基础上,基于一阶滤波算法提出一种可抑制有功功率波动的能量分配策略,并对该分配策略在不同的时间常数下对功率波动的抑制效果进行了仿真验证。仿真结果表明:
①当T=400s时,最大滤波率为3.46%,大于规定值2%;②当T=1000s时,最大滤波率为1.9%,即满足小于2%的要求;③随着T增大最大滤波率减小,但是其成本随之提高,即T无穷大时,无研究意义,综合考虑T=1000s,既能满足要求,又能降低成本。
本研究对我国发电场的发展具有一定的指导意义,在未来的研究中可以进一步考虑通过多源协调风电有功波动抑制方法,改善电网质量,充分利用可再生能源为未来电网调度提供理论基础和实验依据。

