直流偏磁下开磁路电压互感器传变特性仿真研究

王 健， 刘 浩， 刘 俭， 汪根荣， 杜百稳

(中国电力科学研究院有限公司，湖北 武汉 430074)

0 引 言

电力互感器是电力计量、电力系统保护的关键设备，在发电、输电、变电、配电、用电等关键环节，使用大量的电力互感器进行高压大电流的测量和安全保护[1]。随着以高比例清洁能源、高比例电力电子装置为特征的“双高”新一代电力系统快速发展，加上特高压直流输电建设，目前电网中的直流分量影响日益凸显[2]。直流偏磁条件下，电力互感器的暂态特性与稳态传变特性都将发生突变，探究其作用机理，提出进一步的预防措施和治理方案，对确保现代电力系统的安全稳定运行与电能贸易计量的公平公正，具有重要的借鉴意义[3]。

目前，直流偏磁对电力互感器传变特性影响主要聚焦在电流互感器。文献[4]建立了直流偏磁条件下保护用、计量用电流互感器的模型，仿真分析了电流互感器在直流偏磁下的传变特性。文献[5]通过Preisach仿真分析，阐述了直流偏磁对电流互感器的作用机理，揭示了电流互感器在现有偏磁水平下的误差变化规律。文献[6]通过电磁理论分析和试验验证，分析了直流偏磁对电流互感器的误差影响规律，误差曲线向负方向移动。文献[7]基于开气隙双铁心研制了抗直流电流互感器，在直流分量低于10%的条件下，交流误差小于0.2%。文献[8]则采用超微晶和硅钢片两种铁磁材料设计了双铁心结构，研制的微型互感器误差优于0.5%。

直流偏磁对电流互感器影响研究已逐步趋于成熟，目前已有抗直流电流互感器成熟产品，正在推广应用，而对电压互感器在直流偏磁下的传变特性研究较少。电压互感器的工作磁密较高，如果出现直流分量，很容易造成电压互感器磁饱和。同时电压互感器的一次侧绕组线径较小，如果直流偏磁含量过大，会造成互感器烧毁，在电气化铁路中较为常见[9]。

本文将分析电流偏磁对电压互感器计量误差的影响，基于开磁路新型电压互感器原理提升抗直流性能；建立25 kV开磁路电压互感器仿真模型，对计量误差和抗直流性能开展仿真分析；设计误差补偿电路，以提升电压互感器的计量准确度。

1 直流偏磁对电压互感器计量误差影响

电压互感器等效电路如图1所示。其中T为1∶1理想变压器，Z1为互感器一次绕组的直流电阻和漏抗，Z2为二次绕组等效到一次的直流电阻和漏抗，Zm为互感器的励磁阻抗，I0是流经励磁阻抗的励磁电流，Zb为等效到互感器一次的负荷阻抗。

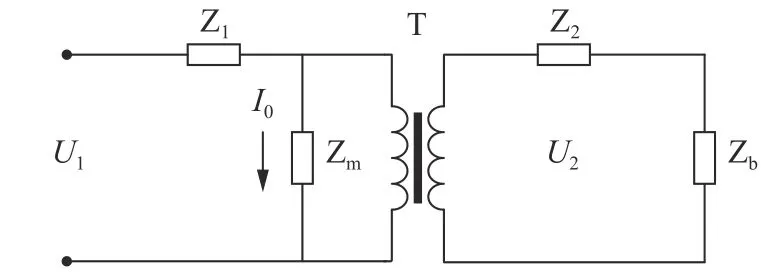
图1 电压互感器等效电路

根据电压互感器误差定义，误差由励磁误差和负载误差组成，可以表示为：

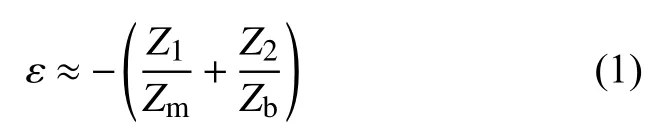
电压互感器一般用于计量，对准确度要求较高，重点考察其传变特性，在不同工况下的励磁曲线如图2所示。

图2 电压互感器在不同情况下的励磁曲线

在直流偏磁作用下，直流电流流入到电压互感器一次侧绕组，在电压互感器铁心中产生了直流磁通Φ0，在Φ0的作用下，磁通Φ的曲线将发生偏移，从而使电压互感器的工作点从线性区进入到了饱和区，励磁电流I0增大，而且发生了畸变。由此看出，有直流分量时励磁电流I0的畸变是由电压互感器Φ-I0曲线端部的非线性引起的，此时互感器处于饱和状态，因此，励磁电流特性除了与电压互感器的设计参数相关外，还与直流电压的幅频特性密切相关。

2 开磁路电压互感器电磁理论分析

为了限制直流偏磁对电压互感器计量准确度的影响，设计了“T字型”铁心的开磁路电压互感器，结构如图3所示。铁心由圆柱体和长方体两部分组成，圆柱体底面位于长方体顶面正中心，且圆形底面的直径与长方体宽度相同，一次和二次绕组呈上下排列，依次绕制在圆柱形铁心上。

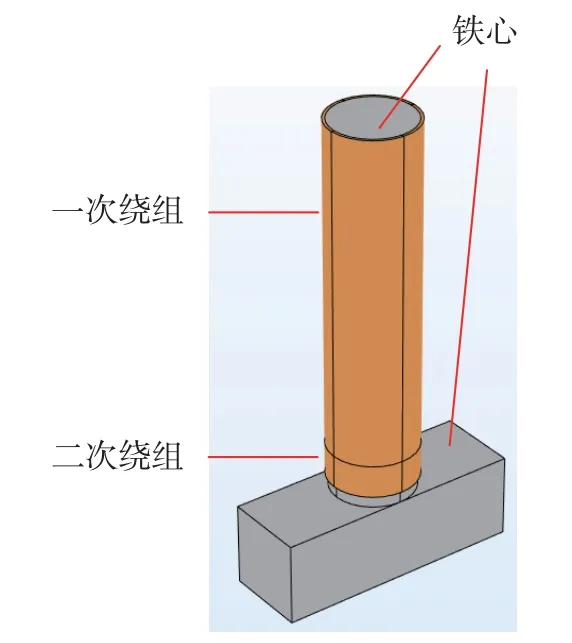
图3 开磁路电压互感器结构图

电压互感器的功能是将一次电压按照匝数比变换为二次电压，而电压变换的精确程度则主要取决于铁心的材质和结构特性。对于开磁路电压互感器，基于其对称结构，取一半进行分析，如图4所示，由于空气磁导率远小于铁心材料，空气中磁力线分散性极大，不存在类似于铁心中较为明显和集中的磁路。为定性分析开磁路结构对电压互感器工作特性的影响，将空气域中磁场分布等效为一条集中磁路，等效长度设为；忽略铁心的漏磁，且不考虑铁心与空气交界面的边缘效应，则可设铁心中磁路等效长度为，则对于铁心和空气磁路，磁感应强度相同，有如下公式：

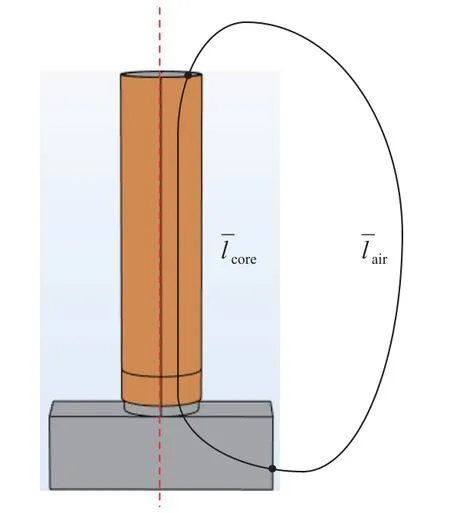
图4 开磁路电压互感器理想磁路示意图

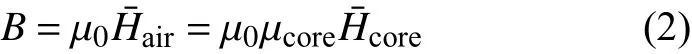
式中：B——磁感应强度；

μ0——真空磁导率；

μcore——铁心相对磁导率。

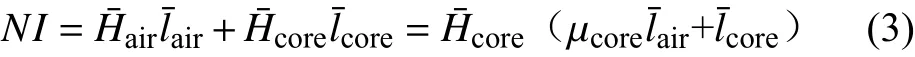
因此，在材料参数相同情况下，“T字型”铁心的开磁路电压互感器，其一次电流相对于闭合磁路电压互感器增大为(1+αμcore)倍，由于μcore＞＞1，则空气磁路可以明显提升抗直流偏磁能力。但是在增强抗直流偏磁能力同时，磁回路的等效磁导率下降，影响互感器的测量精度。

以上针对开磁路电压互感器进行的电磁分析，前提条件是假设空气中磁场沿确定长度磁路集中分布，且不考虑铁心漏磁。由于开磁路电压互感器的结构和材料特性，简化前提条件实际无法满足，导致开磁结构对电压互感器工作特性影响无法通过式(4)定量计算，因此拟采用数值计算方法针对开磁路电压互感器的传变特性开展分析。

3 25 kV开磁路电压互感器磁场仿真分析

本文以电气铁路用25 kV互感器为例，基于有限元方法对开磁路电压互感器的磁场分布和误差特性进行计算分析。

3.1 25 kV开磁路电压互感器参数设计

首先针对25 kV开磁路电压互感器进行参数设计，主要有额定电压、额定负荷、准确度等级、匝电势选取、额定工作磁密。其中，匝电势对互感器成本、误差都有直接影响，考虑到开磁路电压互感器励磁电流较大，因此本设计中的匝电势较常规互感器需更低，选定的参数如表1所示[10]。

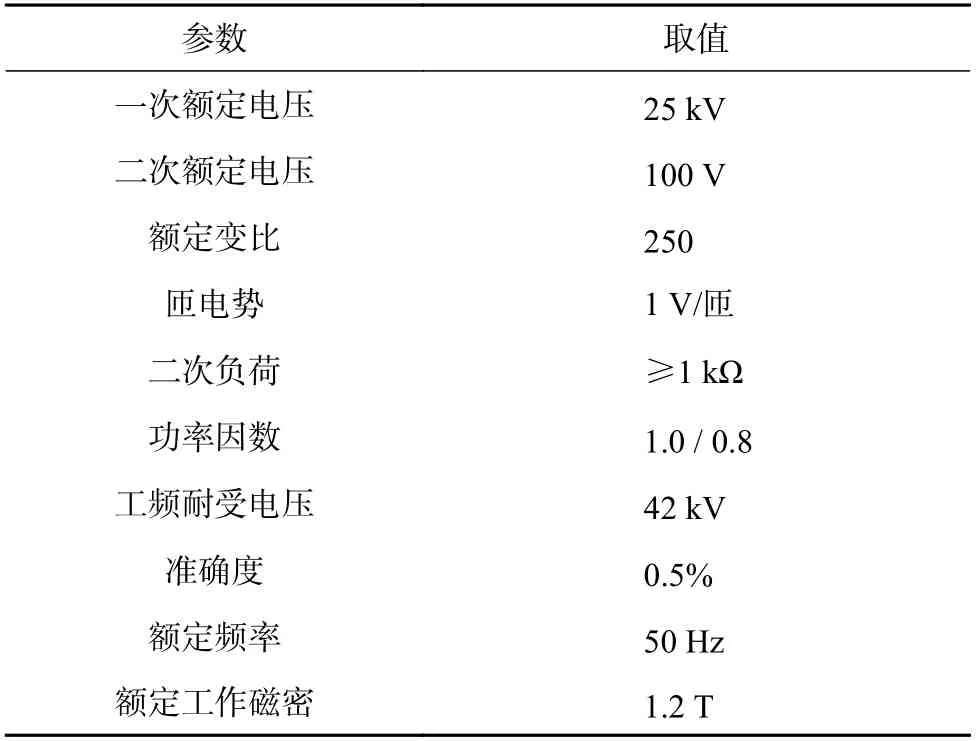
表1 25 kV开磁路电压互感器参数

3.2 25 kV开磁路电压互感器计算模型

由于互感器铁心为软磁材料，具有非线性磁化特性，因此基于瞬态场方程，针对工频电压和直流偏磁电压叠加激励下的互感器磁场开展计算，认为导磁介质各向同性，同时忽略磁滞效应，控制方程如下：

由于内层变化较慢，教师信念建构是一种长期的意识变化[4]，教师职业发展必然体现出长期逐渐进步的过程[5-6]。不从历时角度进行过程研究很难揭示教师职业发展的规律，而当前相关研究缺少历时研究[7]，因此，开展历时研究，探讨外语教师信念建构过程及其对外语教师职业发展的影响非常必要。

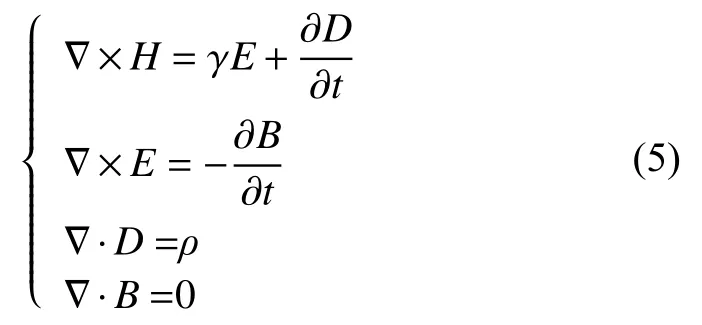
引入矢量磁位A和标量电位φ，其中，E=

开磁路电压互感器有限元模型包括1个铁心以及2个绕组，由于一次绕组和二次绕组的匝数分别为25 000匝与100匝，不能对每一匝线圈都进行建模，因此将整个线圈的外缘作为整体，采用“线圈”接口定义绕组参数，将一次和二次绕组设置为均匀多匝线圈，导线直径0.5 mm。

建模忽略了开磁路电压互感器内部的一些次要结构，在互感器四周构建一个球体用于表示空气域，球体半径为互感器铁心高度的5倍，由于互感器和空气域都具有对称结构，为了减小计算量，基于竖直方向对称轴，取完整研究对象的1/4作为计算域，最终得到开磁路抗直流偏磁电压互感器有限元计算模型如图5所示。

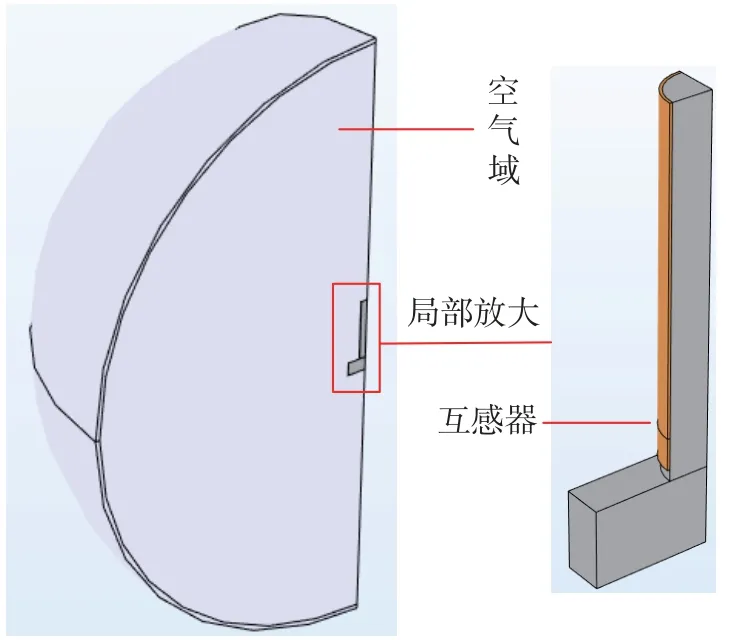
图5 开磁路电压互感器有限元模型

3.3 有限元计算前处理设置

1)材料属性

对开磁路电压互感器，铁心添加硅钢材料，两个绕组设置为铜，其余部分添加空气材料。硅钢为软磁材料，具有非线性磁化特性，其B-H曲线如图6所示。“T字型”铁心与常规互感器叠片铁心不同，在制作时由完整的长方体坯料通过车铣工艺制成，因此电导率很大，各计算域对应材料计算参数如表2所示[11]。

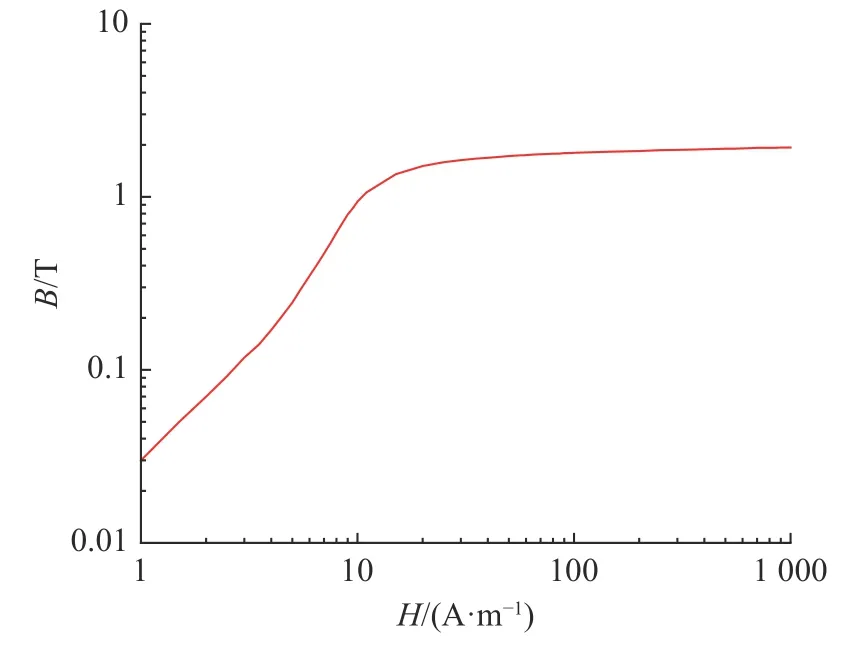
图6 B30P105硅钢B－H曲线

表2 材料参数

2)物理场和边界条件

选择“磁场”物理接口对开磁路电压互感器磁场进行仿真分析。空气与绕组中的磁场本构关系选择磁导率，铁心中的磁场本构关系选择B-H曲线。

对于完整的球型计算域，其外部边界全部设置为磁绝缘，在进行1/4分割后，在新产生的外部边界面上，磁力线与边界平行，因此在这些边界上同样设置为磁绝缘。在实际运行过程中，铁心接地，因此铁心设置为地电位。由于自变量是矢量磁势A，为了保证计算解的唯一性，对计算域添加库伦规范，其实质是对矢量磁势A添加以下限制条件：

3)剖分设置

由于绕组尺寸较小，因此设置其最大单元网格大小为1 mm。铁心顶部以及长方体铁心两侧面处磁导率变化较为剧烈，导致磁通密度梯度较大，因此在附近进行网格加密，以提高计算准确度。网格剖分结果如图7所示。

图7 网格剖分结果

4)激励和负载条件

本文需要研究开磁路电压互感器的抗直流性能，因此对一次绕组的激励为工频正弦电压和直流偏磁电压的叠加量，激励电压Uin取值为：

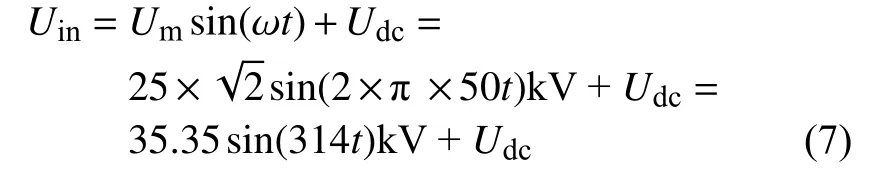
式中：Um——开磁路电压互感器的额定正弦工频电压峰值；

Udc——开磁路互感器的直流偏磁分量，取值在下文进行说明。

互感器负载取5 VA，功率因数cosφ=1，通过“电路”接口在二次侧连接一个2 kΩ电阻。

3.4 磁场分布特性

由于要求25 kV电压互感器抗直流水平达到2.5 kV[9]，因此Udc取值区间设置为0～4 kV，间隔1 kV。

完成开磁路电压互感器电磁场有限元计算后，得到磁通密度分布情况，如图8所示，Udc=1 kV，磁通密度最大时刻，空气域以及铁心中磁密的分布情况。

由图8可以看到，绕组中的磁通密度铁心中的磁通密度；将“T字型”铁心大致划分为圆柱体和长方体上下两部分，铁心磁通密度较大值主要位于圆柱形铁心中间部分，且圆柱形铁心顶部磁通密度小于中间部位，长方体铁心大部分区域磁通密度较小，但与圆柱形铁心连接部位也有一部分磁通密度较大；铁心上磁通密度最大值为圆柱形铁心与长方体铁心交界面的外部边线，出现这种情况的原因是铁心加工过程造成的交界部位呈90°夹角，磁力线在此处集聚，由圆柱形铁心进入空气和长方体铁心，最终出现磁通密度最大的现象。

图8 开磁路电压互感器磁通密度分布

为了进一步说明开磁路电压互感器磁场分布特性，绘制6.5 ms时刻磁力线分布如图9所示，其他时刻类似。磁力线在通过圆柱形铁心后主要有两个分支，第一个分支在圆柱形铁心下端部侧面离开铁心，沿着靠近圆柱形铁心外壁的空气域进入铁心顶部，第二个分支进入长方形铁心，在长方形铁心侧表面离开铁心，沿着稍远离圆柱形铁心外壁的空气域进入铁心顶部，表明开磁路电压互感器的漏磁较为严重。

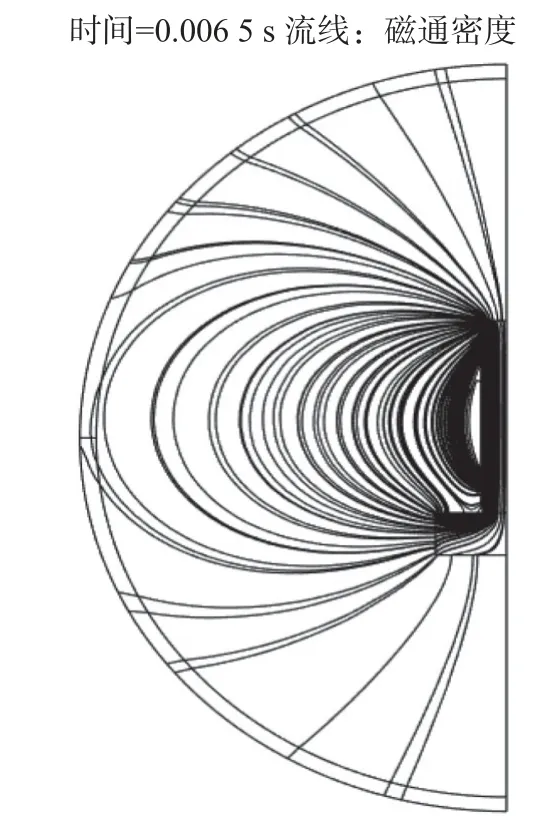
图9t=6.5 ms时磁力线分布

4 误差计算与补偿设计

4.1 开磁路电压互感器误差特性

在前述模型的基础上，分别计算不同直流偏磁电压下开磁路电压互感器的一、二次电压波形，如图10所示。

图10 不同直流偏磁电压下互感器电压波形

由图可知，直流分量为0时，由于铁心励磁支路的非线性造成的二次波形畸变并不明显，随直流分量增大，二次电压大小增大、波形畸变严重，从而造成铁心的传变特性变差，致使电能计量与测量出现偏差，给电力公司带来巨大的损失。

为了分析直流偏磁对互感器比差和角差的影响，对仿真得到的一次电压和二次电压(折算到一次侧)的波形运用三参数正弦曲线拟合算法，可得到系数A1(余弦函数幅值)、B1(正弦函数幅值)及A2、B2，最终可计算得到互感器在不同直流偏磁电压下的误差，如表3所示[12-13]。

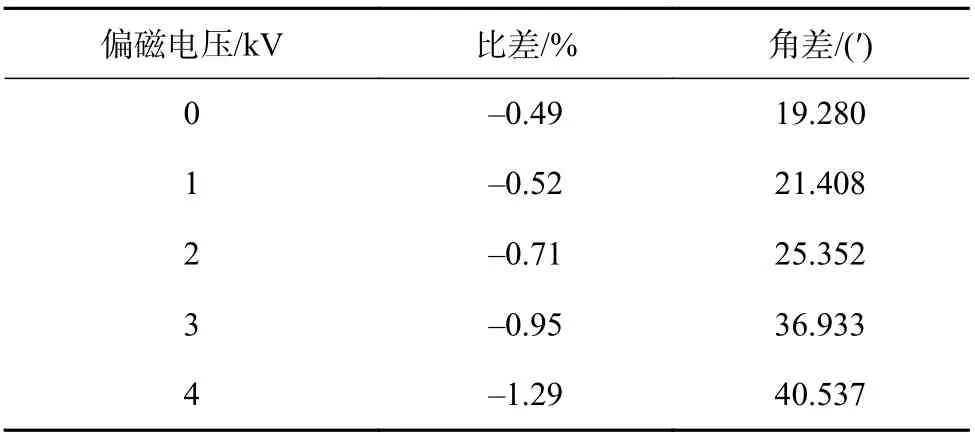
表3 不同直流偏磁电压下互感器误差

4.2 误差补偿设计

作为计量用电压互感器，对精度要求较高，一般需要达到0.5级，表4给出了0.5级电压互感器的误差限值。

表4 0.5级电压互感器误差限值表

由前文仿真结果可知，开磁路电压互感器虽然具备抗直流性能，但其计量误差已超出0.5级误差限值，需要对其进行误差补偿。设计一种误差补偿方法，原理线路图如图11所示[14-15]。

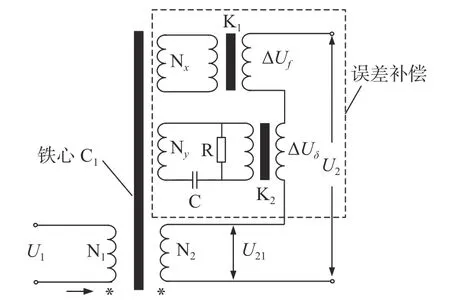
图11 开磁路电压互感器误差补偿原理

在铁心C1上取Nx和Ny两处匝电势，Nx用于比值误差补偿，Ny用于相位误差补偿。

1)比值误差补偿

Nx为二次侧低电压，一般为几伏，后端接入一个小型互感器K1(其电压变比为K1)，小型互感器K1的二次侧输出ΔUf用于比值误差补偿。需要说明的是：ΔUf的幅值和相位均可根据需要补偿的目标值进行调整，通过调节小型互感器K2的匝数来调节互感器变比K2，实现比值误差补偿量的灵活可调；另外改变小型互感器K2的一次、二次极性，改变K2的输出相位（翻转180°），实现相位误差补偿的正负改变。

2)相位误差补偿

相位误差补偿原理类似，不同的是在Ny的后端增加R-C串联移相电路，然后经过小型互感器K1(变比为K1)，小型互感器的二次侧输出ΔUδ用于相位误差补偿。同比值误差补偿一样，ΔUδ的幅值和相位可以根据补偿目标值进行可调。通过调节K2的匝数调整ΔUδ的幅值，改变同名端来调节补偿量的相位。此外，也可调制电阻R的阻值和电容C的容值大小来调节的补偿量ΔUδ的幅值和相位。

基于上述分析，该补偿电路可在开磁路电压互感器的二次侧进行误差补偿，该补偿原理的矢量图如图12所示。

图12 误差补偿矢量图

图中，U21为二次比例绕组N2的输出电压，以此作为参考方向并假定其幅值为单位1，ΔUf为比值误差的补偿量，ΔUδ为相位误差的补偿量，三者矢量合成后的U2为最终输出电压，即需要达到0.2级的最终二次侧电压输出，α为移相电路的移相角度，β为最终的相位误差补偿量。根据相位图关系，可得：

由矢量图可以看出，ΔUδ在进行正交分量补偿的同时，会引入同相分量的误差补偿。因此比值误差补偿量实际上由两部分组成：比值误差补偿本身和相位误差补偿时产生的同相分量。

最终比值误差补偿量Δεf：

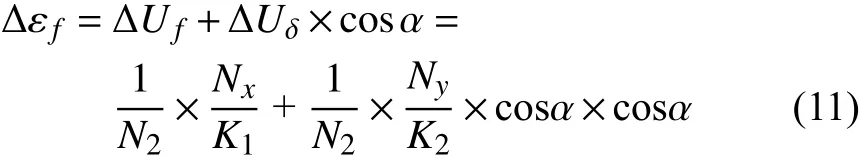
最终相位误差补偿量Δεδ：

根据4.1节所示误差理论计算结果，可得到需要误差补偿的量值，需要对比值误差补偿0.89%和相位误差补偿–29.91′。首先取Nx=9，Ny=2，R=100 Ω，C=30 μF，通过式(8)可得α=π/4。代入式(11)和(12)可得K1=5，K2=1，最终得到开磁路电压互感器误差如表5所示，满足0.5级互感器的误差限值要求。

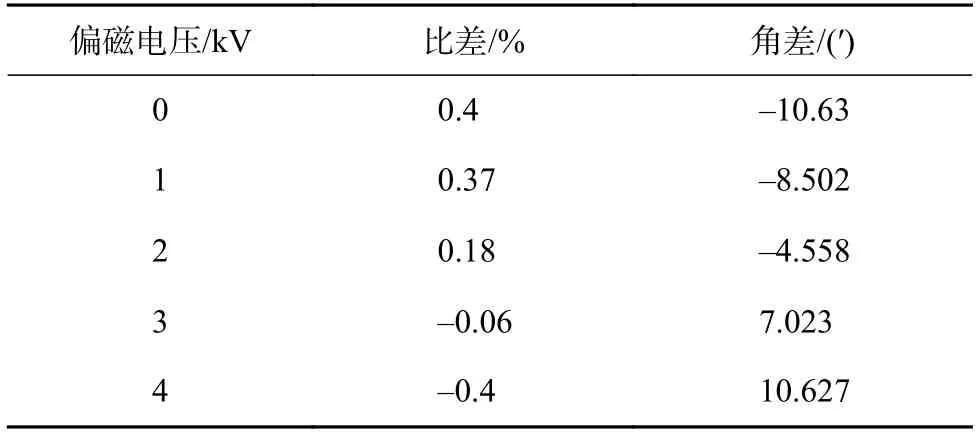
表5 补偿后电压互感器误差

5 结束语

针对传统电压互感器抗直流偏磁能力不足的问题，本文设计了一种开磁路的“T字型”铁心抗直流偏磁电压互感器，定性分析了其抗直流偏磁原理，以电气铁路用25 kV互感器为例，采用有限元方法对比计算不同直流偏磁电压下的互感器磁场分布和误差特性，并设计了同时针对比值误差和相位误差的补偿方法，通过选取合适的补偿电路参数，使开磁路电压互感器误差满足0.5级要求。