基于改进BP算法的用水量预测模型研究
袁玉英 罗永刚 孙立云
(1.山东理工大学计算机科学与技术学院,山东 淄博 255000;2.山东理工大学电气与电子工程学院,山东 淄博 255000)
随着社会的发展,城市居民用水量在快速增加,水资源短缺问题日益严重。因此,对水资源利用进行合理规划、对供水系统进行优化调度十分必要,作为供水管理前提和基础的用水量预测也变得越来越重要[1]。
水量预测工作是水资源管理中关乎未来发展趋势的关键。通过建立用水量预测模型,对城镇规划期限内的用水量进行合理预测,提前掌握城市用水量情况,做好水资源规划,对城市的建设和发展具有极其重要的意义。通过预测未来某个时段的用水量,可以预见城市用水是否有缺口,并着手寻找解决方案,以减少经济损失,因此,根据城市居民用水量的历史数据预测未来某个时段的用水量,在经济效益和宏观调控方面都具有重要意义[2]。本文采用BP神经网络建立用水量预测模型,收集某个时期城市居民用水量的历史数据,利用改进的BP算法对城市居民未来3天的日用水量进行预测,并和实际城市居民日用水量数据进行对比分析,证明了该模型的有效性。该模型自适应调整学习率,结合LM算法,引入动量因子,采用自主设计的训练函数对设计好的网络进行训练,提高了用水量预测的准确率,对本地城市居民用水量预测具有一定的参考价值。
1 模型构建
1.1 BP神经网络原理
BP算法是第一个适合多层网络的学习算法,由P.Werbos于1974年提出,1986年美国加利福尼的PDP小组在神经网络的研究中应用了该算法,使得该算法逐步被研究学者接纳并重视,如果神经网络在训练样本时采用的是BP算法,则称该网络为BP神经网络[3]。
BP神经网络由多层神经元组成。图1是由输入层、隐层和输出层组成的典型BP神经网络模型。网络中数据传输的流向为输入层到隐层再到输出层,因此属于前馈型网络[4]。

图1 典型BP神经网络模型
BP网络有多种传递函数,一般隐层神经元采用非线性传递函数,单极性S(Sigmoid)型函数和双极性S型函数是最常用的非线性传递函数;输出层可以是非线性传递函数,有时也可采用线性传递函数,根据网络输出的取值范围确定[5]。
确定BP神经网络结构后,利用训练样本训练网络,目的是通过学习实现网络权值的修正,从而在输入任意值时得到的输出值最接近期望结果。
BP神经网络的学习过程分为两个阶段:第一个阶段为信号前向计算,在此阶段,输入训练样本,由输入层到隐层再到输出层得到各神经元的输出;第二阶段为误差反向传播,在此阶段,神经元的期望输出和实际输出产生的误差由后至前通过改变权值逐层修正,即误差反传过程[6]。
“信号前向计算”与“误差反向传播”过程反复交替,以实现网络记忆训练,直到全局误差趋于极小值,即达到收敛为止。BP算法也由此而来(误差反向传播,Back Propagation),该算法同样可以在有多个中间层的网络中应用[7]。标准BP算法的学习规则为误差梯度下降算法,即按误差函数梯度下降的方向修正权值。
目前,BP神经网络的应用越来越广泛,但BP算法在应用中也暴露出一定的缺陷,如训练次数多,学习效率低,收敛速度慢;易形成局部极小的情况;预测值与实际值误差较大等。
针对上述缺陷,本文采用如下方法进行改进:
a.改进学习率参数的调整方法。当网络误差E(k)逐渐减小时,尤其减小趋势明显时,则按增量因子kinc增大学习率,以使网络更好地修正权值;当E(k)增加并超过预定值时,按减量因子kdec减小学习率,并在E(k)增加的前一步修正放弃[8],学习率调整公式为
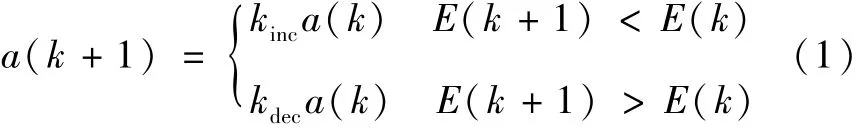
式中:a为学习率。
b.结合LM算法提高收敛速度,减小均方误差,提高精度。LM算法提出的目的是在二阶近似速率下进行修正但避免Hessian矩阵的计算。当采用平方和误差作为误差性能函数时,Hessian矩阵的近似表示式为

计算梯度的表达式为

式中:J为雅克比矩阵,其计算比Hessian矩阵更简单[9];e为网络的误差向量。
LM算法的修正采用上述近似Hessian矩阵,修正公式为
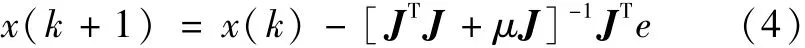
变量μ确定学习是根据牛顿法或梯度法来完成的。当μ=0时,上式即为牛顿法;当μ的值很大时,上式变为步长较小的梯度法。
c.引入动量因子η(0<η<1),在保证算法稳定的同时,收敛速度更快,学习时间更短,满足:

式中:k为迭代次数;x(k)为第k次迭代各层之间的连接权向量或阈值向量;α为学习速率。
由式(5)可知,当前一次修正超过预定值时,∂E(k)/∂x(k)的符号与∂E(k-1)/∂x(k-1)的符号相反,可减小本次修正量,以减小振荡;反之,两者符号相同,可增大本次修正量。因此,本次修正量的大小会受到前一次修正结果的影响。
1.2 用水量预测模型结构的建立
在本设计中建立用水量预测模型时,采用三层BP神经网络:第一层为输入层,第二层为隐层,第三层为输出层。本设计选用北方城市某小区2020年6月1—30日的用水量数据作为历史数据,训练样本集的数据为6月1—20日的数据资料,测试样本集的数据为6月21—27日的数据资料,将每天划分为12个时段,每2h为一个时段,每个输入分量对应一个时段,因此输入层需要12个神经元。对于隐层,采用试凑法确定隐层节点数,先设置较少的隐节点训练网络,然后逐渐增加隐节点数,用同一样本集进行训练,确定网络误差最小时对应的隐节点数即为隐层节点数。在确定试凑法初始值时,采用m=log2n(式中:m为隐层节点数;n为输入层节点数)经验公式设置初始值。表1为隐节点数目变化时平均百分比误差变化的情况。实验发现,在隐节点数目较少时,网络性能不稳定,有时会出现平均百分比误差较大的情况,同时平均百分比误差总体偏大。综合考虑网络的误差、训练时间、网络稳定性及结构等因素后,最终确定隐层节点数为8。对于输出层,根据过去一段时间的历史数据,确定为未来3天的用水量,因此,输出层需要3个神经元。

表1 隐节点数目变化时平均百分比误差变化的情况
隐层神经元的传递函数采用单极性S(Sigmoid)型函数:

输出层神经元的传递函数采用pureline函数。
2 模型训练与测试
2.1 模型训练
将北方城市某小区2020年6月1—20日共(20×12)个时段的用水量数据作为训练数据,6月21—27日(7×12)个时段的用水量数据作为测试数据。该小区为大型综合小区,其用水特点和一般的纯居住类小区不同。以上数据来源于该小区水表总表抄表数据。图2为该小区2020年6月的分时段用水量曲线。

图2 某小区2020年6月分时段用水量曲线
由于隐层选取的传递函数为S型函数,其输出范围为(0,1.0),输出值为0.5时,导数可达最大,且给定权值的变化与导数相关,所以为避免隐层输出集中在饱和区域从而使收敛减慢,将训练数据进行归一化处理,归一化公式为

式中:x为待训练的实际用水量数据,m3;xmax、xmin分别为其最大值和最小值,m3;ymax、ymin分别为期望的最大值和最小值,m3。当x取xmax或xmin时,上式中的ymax取值0.6,ymin取值0.4;对于其他输入数据,ymax取值1.0,ymin取值0。
图3为预处理后的待训练用水量数据。从图3中可以看出,预处理后的结果在0~1之间变化,但避免为0或1。在利用训练数据对神经网络进行训练时,设置相关训练参数如下:初始学习速率为0.01,学习率增量因子为0.70,学习率减量因子为1.05,动量因子参数为0.9,μ的初始值为0.001,μ的增量因子为10.0,μ的减量因子为0.1,μ的最大值为1010。对权值和阈值初始值赋随机数。在设置好相关训练参数后,采用自主设计的训练函数trainlmgd对设计好的网络进行训练。
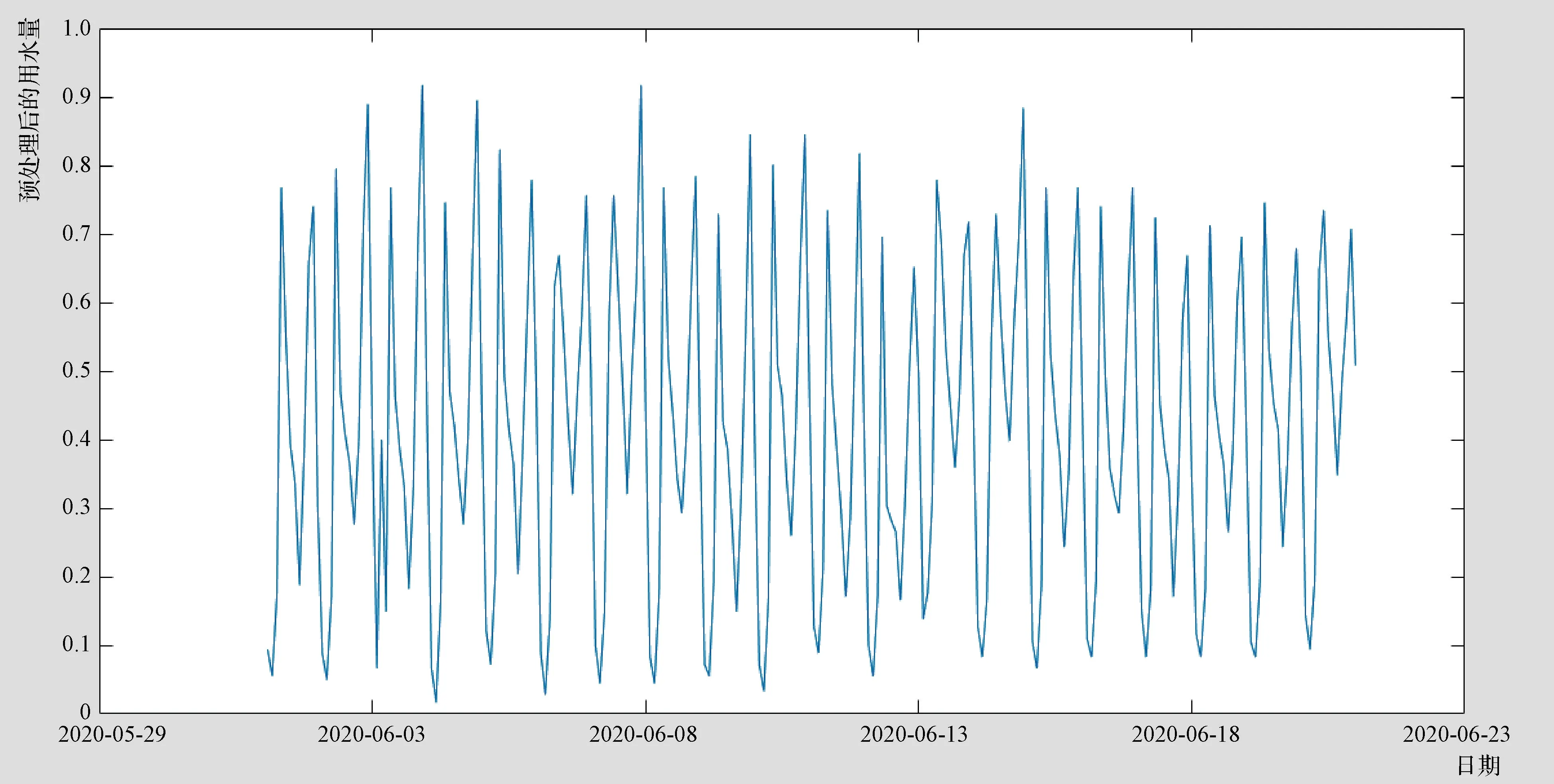
图3 预处理后的待训练用水量数据
2.2 模型测试
利用6月21—27日(7×12)个时段的用水量数据作为测试数据。经该网络测试后反归一化,与6月22—30日的实际日用水量总和进行对比,以平均百分比误差MAPE作为模型评价指标。平均百分比误差计算公式为
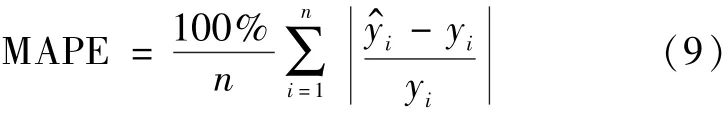
表2为总平均百分比误差为0.0657时,6月21—27日预测的未来3天的日用水量数据与真实数据的对比情况。
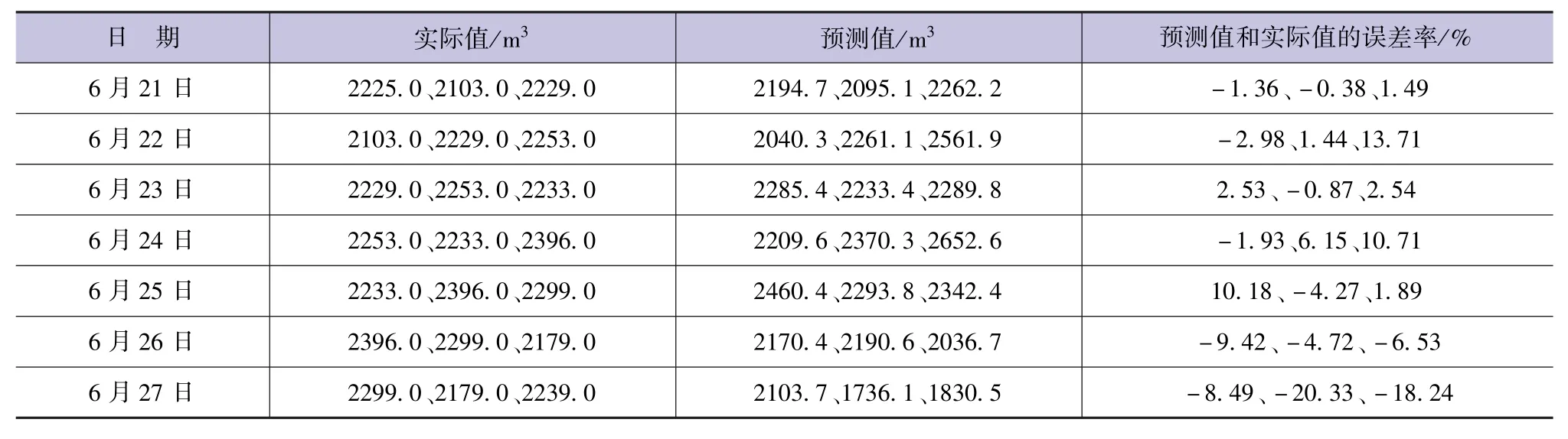
表2 未来3天日用水量预测值与实际值比较
从表2可以看出,除个别数据外,利用建立的用水量预测模型可以较好地预测未来3天的日用水量数据,预测结果满足精度要求,模型精度较高。
另外,通过实验发现,采用传统的BP算法和学习率可变的动量BP算法建立的用水量预测模型在进行预测时,每次轮训都是在达到最大训练次数10000次时结束,很显然达不到预测效果。而采用本设计中改进的BP算法与LM算法时,在训练次数为100次附近时,就可达到1×10-12的性能指标。
图4为采用本设计中改进的BP算法与LM算法建立用水量预测模型时所得结果的对比情况。
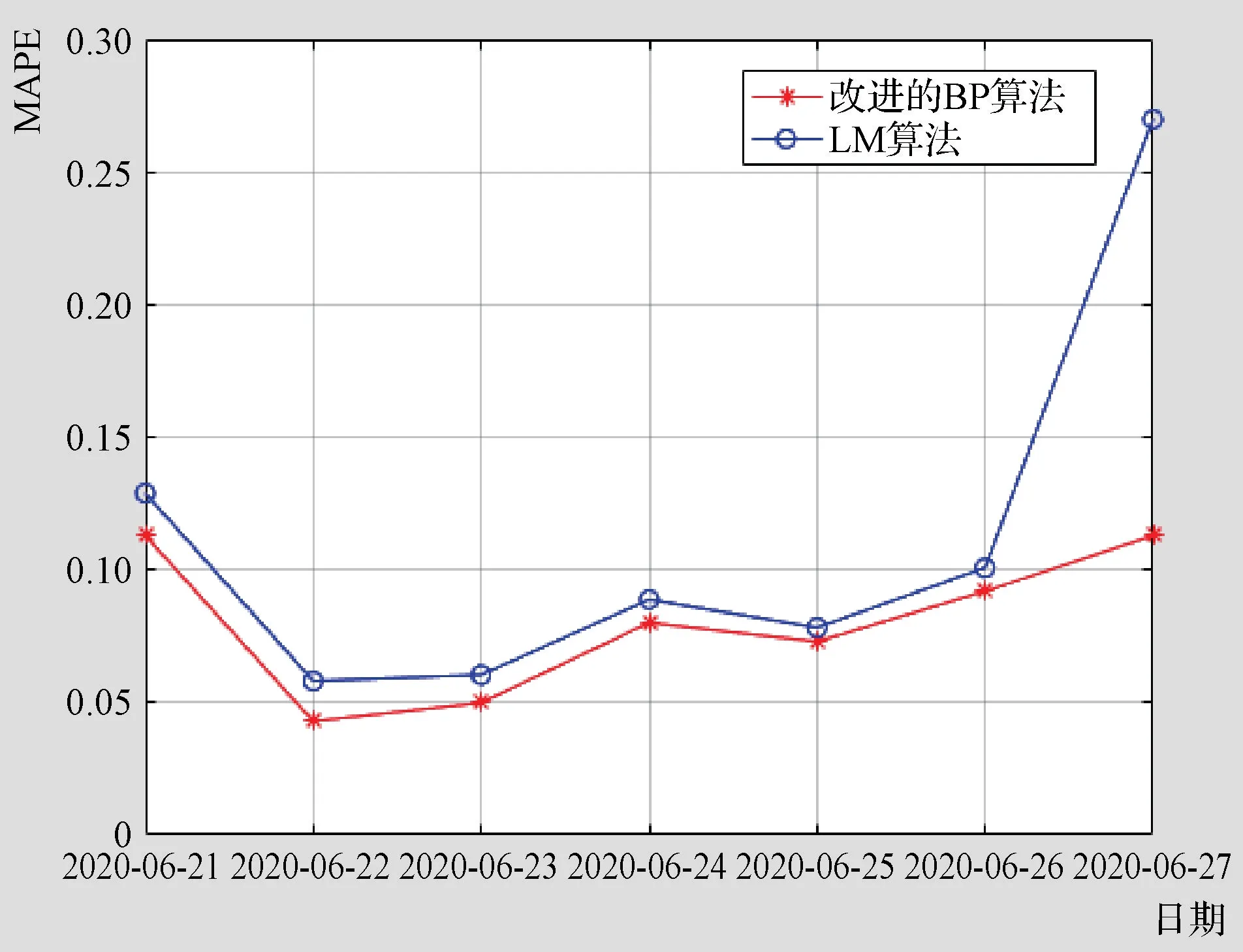
图4 改进的BP算法与LM算法预测结果的对比情况
另外,输入层神经元数目对预测结果也有很大影响。如果输入层神经元取24个,即每1h为一个时段,这时隐层神经元数再取8,将使预测平均百分比误差较大,因此仍采用试凑法确定隐层神经元数为14。图5为输入层神经元数分别为24个和12个时的10次轮训所得平均百分比误差。由图5可知,前者误差明显小于后者,这说明对某一段时间内的数据划分越细,预测结果越准确。
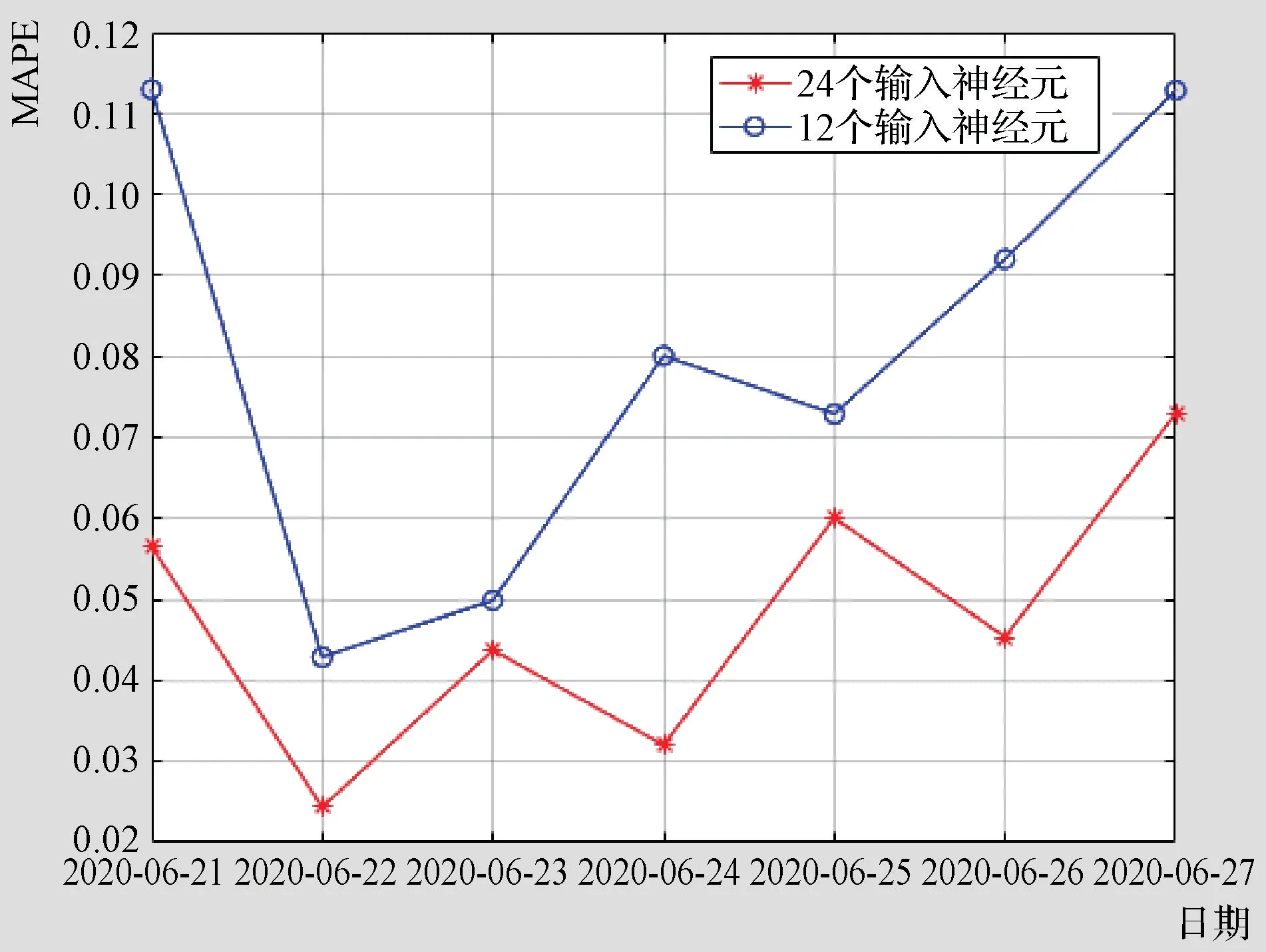
图5 输入层神经元数变化时预测误差的比较
3 结 语
建立三层BP神经网络,通过实验对比,确定每层神经元数分别为12、8、3,有效简化了部分网络结构。基于改进的BP算法建立用水量预测模型,自适应调整学习率,结合LM算法提高收敛速度,同时引入动量因子,自主设计训练函数对设计好的网络进行训练。采用北方城市某小区的样本数据进行训练,测试后预测精度达到要求。实验表明,该用水量预测模型与采用标准BP算法的模型相比,训练次数少,训练误差小,训练精度高,收敛速度快,网络稳定。鉴于样本数量的限制,如果增大样本数量,预测精度将会更高。■

