参数不确定性下高效的可靠性灵敏度分析方法

陈志远,李璐祎

西北工业大学 航空学院,西安 710072

灵敏度分析是研究和分析系统或模型的状态或输出响应对输入参数和周围条件的敏感性,它包括局部灵敏度分析和全局灵敏度分析。局部灵敏度分析通过保持参数在名义点处的值,每次改变一个输入参数来检查输出的局部响应,因此它不能考虑输入变量与其他输入参数的交互影响对输出响应的影响。全局灵敏度分析可以综合考虑基本变量在其不确定性范围内单独变化以及与其他变量交互作用对输出响应的平均影响,因此在工程设计和概率安全评估中取得了广泛的运用。全局灵敏度分析起源于Cukier等于1973年提出的几种不确定灵敏度指标,随后得到了迅速发展,如Helton提出了非参数技术,但该方法缺少模型的独立性；为了度量输入变量的不确定性对模型输出方差的影响,Sobol、Saltelli等提出了基于方差的全局灵敏度指标,之后出现了各种各样方差灵敏度简明高效的计算方法,例如：高维模型替代法(RS-HDMR)、状态相关参数法(SDP)、随机平衡设计过程(RBD)、基于蒙特卡洛的数值模拟法(MCS)等。为了分析基本变量对输出整体分布的影响,Borgonovo等提出了基于概率密度函数的全局灵敏度指标。Li等之后将灵敏度指标引入到可靠性分析领域,提出了全局可靠性灵敏度指标。接着Wei等在Li等的基础上进一步对可靠性灵敏度的定义进行了标准化,定义各输入变量的主灵敏度和总灵敏度指标。Yun等将分数矩约束下的最大熵理论与Nataf转换相结合提出了一种估计全局可靠性灵敏度指标的方法；蒋献等通过Edgeworth级数展开将失效概率矩独立全局灵敏度指标的求解转化为输出无条件及条件前四阶整数矩的求解；Shi等提出了一种将稀疏网格技术与四矩法结合来估计全局可靠性灵敏度的方法。

上述方法都是在假设输入变量的分布参数是已知的情况下进行的,即只考虑了输入变量的不确定性。然而在工程实际中,正如Xu等所分析的,由于数据缺乏或条件限制,导致输入变量分布参数不能准确确定,即分布参数也具有不确定性。分布参数不确定性被Ditlevsen、Haldar和Hajagos等称为统计不确定性和二阶不确定性。根据掌握的信息量多少,分布参数的不确定性通常可以采用区间、模糊隶属函数、主观概率密度函数等进行描述。确定性分布参数下模型输出统计特征是确定的,如均值和方差；而分布参数不确定性会导致输出统计特征也具有不确定性,因而输入对输出的影响也是不确定的,并由输入变量的不确定性和分布参数的不确定性同时控制。因此,在灵敏度分析过程中,为了准确识别对输出影响较大的输入变量,就必须同时考虑输入变量的分布参数在整个不确定范围内对模型的影响。

目前,关于分布参数不确定性情况下基于方差的灵敏度分析已有一些研究。实现分布参数不确定性下的灵敏度分析的一个基本方法是三层嵌套Monte Carlo(MC)抽样方法。该方法将分布参数在外层进行采样,随后在内层进行双层循环抽样以计算随机输入变量的灵敏度指标。但是这种方法计算成本过于高,不能直接用于实际工程问题。随后,Saltelli等通过引入单层循环MC抽样将三层嵌套MC抽样简化为双层嵌套抽样,在一定程度上减少了计算量,但是对于实际工程问题来说计算量还是过于庞大。Li等通过将代理抽样密度函数与单层MC相结合,进一步将三层嵌套循环简化为单层抽样,能用较少的抽样点得到精确的灵敏度估计结果。

以上都是参数不确定性下基于方差的全局灵敏度分析,这种灵敏度分析方法隐含地假设方差这一单一矩足以体现输出的不确定性变化。但是,当分布被描述为某个具体的数值时,必然会造成信息的缺失。另外,在可靠性分析领域,工程实际更关心失效概率。大多数小失效概率与输出的尾部分布有关,基本变量对输出方差的影响并不等同于对失效概率的影响。Tang等利用失效概率(PFD)的互补累积分布函数定义PFD超过给定值的概率,分析了安全仪表系统(SIS)中具有截断分布的认知不确定输入参数对超出概率的影响。Chabridon等将参数不确定性下失效概率分布的平均估计(PFP)作为一种新的安全度量进行灵敏度分析,并提出了一种与自适应重要抽样相结合的PFP估计策略；但该方法对于多失效域与高维问题所需的计算量非常庞大,计算效率较低。因此,为了准确评估参数不确定性下输入变量对结构失效概率的影响,就需要发展新的基于可靠性的灵敏度指标及其求解高效的算法。

不同于基于方差的灵敏度分析,参数不确定性情况下基于可靠性的灵敏度分析一般需要在每个参数取值处重复进行可靠性分析,计算量难以为工程实际所接受。尤其是对于小失效概率结构系统,提高可靠性灵敏度分析效率一直是一大难点。因此,本文主要研究参数不确定性下输入变量高效的可靠性灵敏度分析方法。所提方法首先将基于可靠性的全局灵敏度指标扩展到输入变量及其分布参数同时具有不确定性的情况,定义了参数不确定性情况下输入变量的主灵敏度指标以及总灵敏度指标。然后借鉴文献[40]中的基于方差的灵敏度指标求解的单层抽样方法,将参数不确定性情况下基于可靠性的灵敏度指标求解过程中的三层嵌套可靠性分析简化为单层抽样分析,极大地减少参数不确定性下可靠性灵敏度分析的计算量,并针对小失效概率问题,进一步将单层可靠性灵敏度分析与可靠性分析高效的重要抽样(IS)以及截断重要抽样(TIS)结合起来。

本文所提方法的创新点分列如下：

1) 将基于方差的灵敏度分析的单层抽样方法进一步扩展到可靠性分析领域。

2) 通过构造合适的重要代理抽样概率密度函数(Surrogate Sampling Probability Density Function,SS-PDF),将单层可靠性灵敏度分析与高效的IS和TIS方法结合起来,解决参数不确定性情况下小失效概率结构系统基于可靠性的灵敏度分析计算代价大的问题。

1 参数不确定性下基于可靠性的全局灵敏度指标

1.1 基于可靠性的全局灵敏度指标

={:()≤}

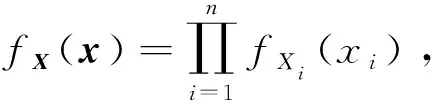
(1)

相应的失效域指示函数定义为()：

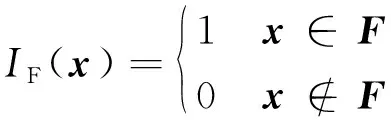
(2)

结构系统的失效概率可表示为

(3)

式中:表示输入变量的维空间。基于可靠性的全局灵敏度指标定义为

f|)()d

(4)

式中:f|=(|)为消除不确定性下的条件失效概率;代表一个随机基本变量或者一组随机基本变量(,…,), 1≤≤…≤≤。

文献[22]进一步证明了：

(|)]}=[(|)]

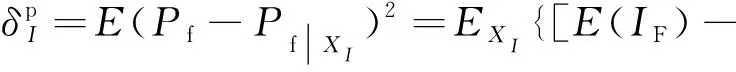
(5)

式(5)表明：当将看作是模型输出时,输入变量基于可靠性的全局灵敏度指标就等同于失效域指示函数基于方差的全局灵敏度指标；因此,文献[25]中定义了正则化的可靠性灵敏度指标：

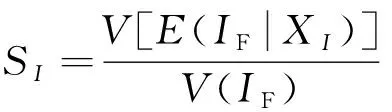
(6)

其中单个输入变量的主灵敏度指标为

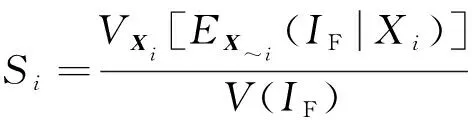
(7)

总灵敏度指标为

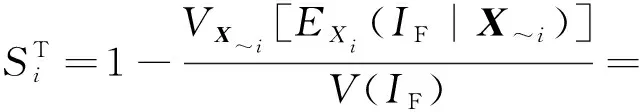
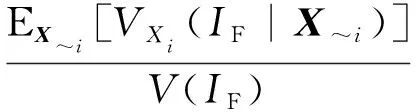
(8)

式中:～为包含除了外的所有输入变量。

1.2 参数不确定下全局灵敏度指标定义

当输入变量=[,,…,]的分布参数受认知不确定性影响,计算模型将会同时包括分布参数的认知不确定性以及输入变量的随机不确定性。设=[,,…,]是输入变量的维分布参数,其中是输入变量相应的维分布参数,且++…+=。分布参数的认知不确定性可以有很多种表示形式,类似于文献[30],本文采用概率密度函数()来描述输入参数的认知不确定性。对于一个由()产生的认知参数,随机输入变量是通过条件概率密度函数(|)产生的。

当输入变量的分布参数具有不确定性时,式(6)～式(8)中输入变量对结构失效影响的可靠性灵敏度指标也不再是一个确定的值,而是一个随着的分布参数的变化而变化的变量。为了准确衡量参数不确定性下输入变量对失效概率的影响,就需要全面考虑输入变量在整个参数空间内对失效概率的平均影响。因此,分布参数不确定性下输入变量基于可靠性的主灵敏度和总灵敏度指标表示为

(9)

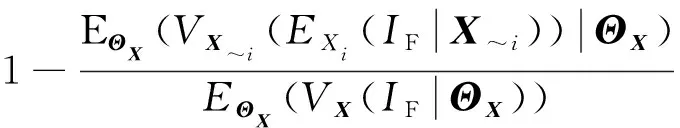
(10)

式中:((|))=()是无条件方差。

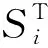
2 参数不确定性下基于可靠性的灵敏度指标的高效算法

式(9)、式(10)表明,参数不确定性下基于可靠性的灵敏度指标的直接求解需要三层循环嵌套的可靠性分析。即使对于分母中的无条件方差(),也需要双层嵌套的可靠性分析过程,即在外层通过认知参数的边缘密度函数对输入变量的分布参数进行抽样,内层在每一个参数的取值处进行可靠性分析得到条件方差(|)。这种嵌套的可靠性分析由于计算量很大并不适用于工程实际问题中。本节提出了参数不确定性下基于可靠性的灵敏度指标求解的3种高效算法。

2.1 代理抽样蒙特卡洛法(S-MCS)

2.1.1 无条件方差的计算

其中无条件方差()可以转化为

()=((|))=

(11)

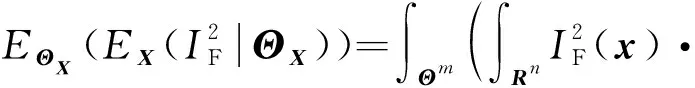
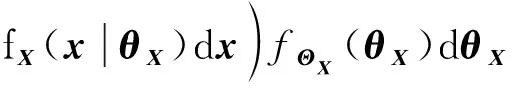
(12)

式中:表示参数的维空间。

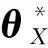
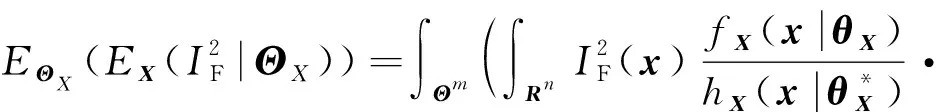
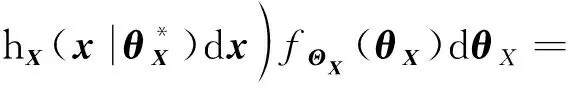
(13)

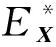
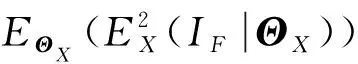
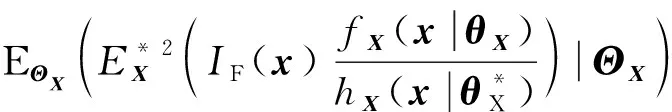
(14)

2.1.2 主灵敏度指标和总灵敏度指标的计算

将式(11)中的总方差公式应用于(～(|))后可以得到：

((～(|))|)=

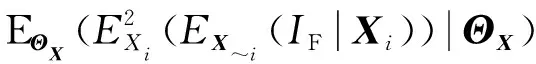
(15)

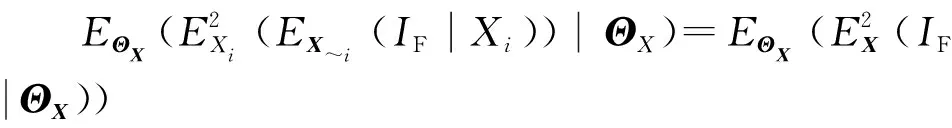
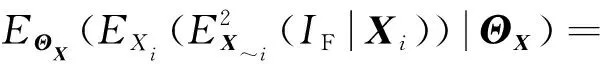
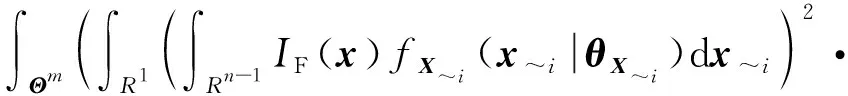
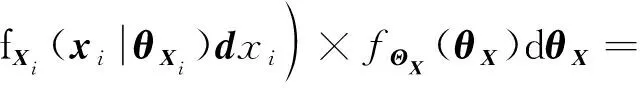
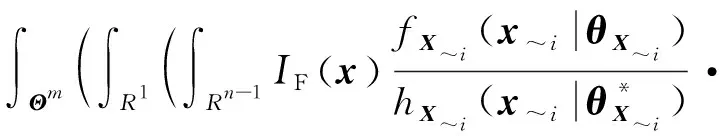
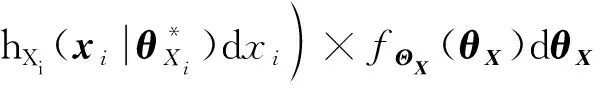
(16)

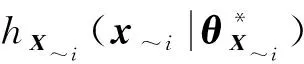
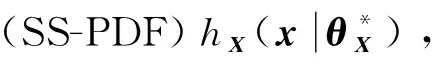
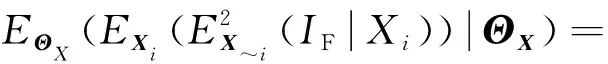
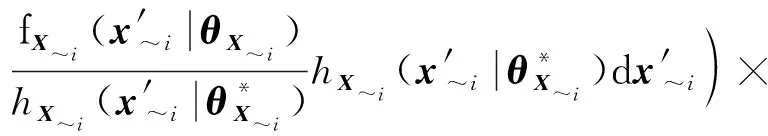
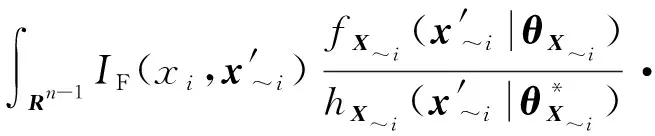
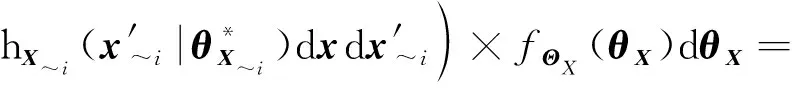
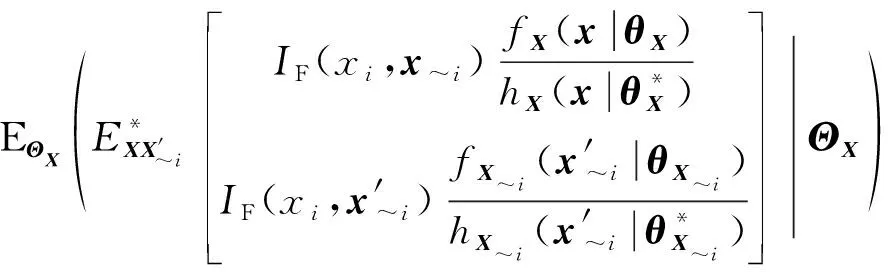
(17)

(～((|～))|)=

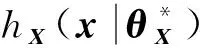
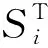
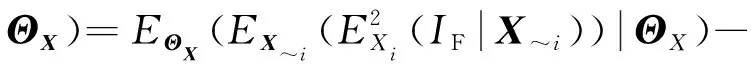
(18)

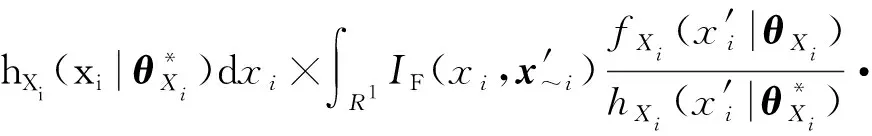
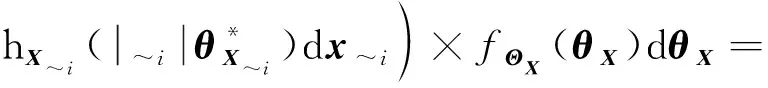
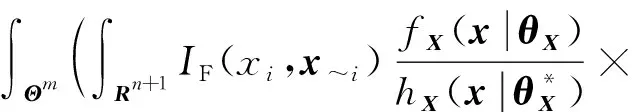
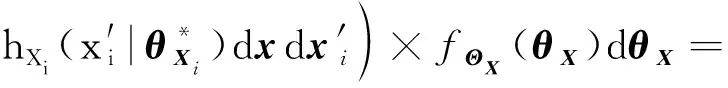
(19)

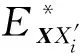
2.1.3 代理抽样密度函数(SS-PDF)的选取

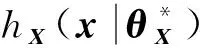
(20)

2.1.4 S-MCS抽样步骤

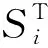
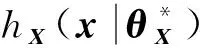
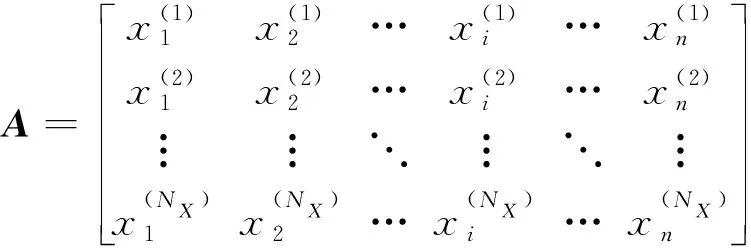
(21)

(22)

2) 产生另一个×维样本矩阵(),()中除第外的其他所有列是来自矩阵,第列中的元素是来自于矩阵:

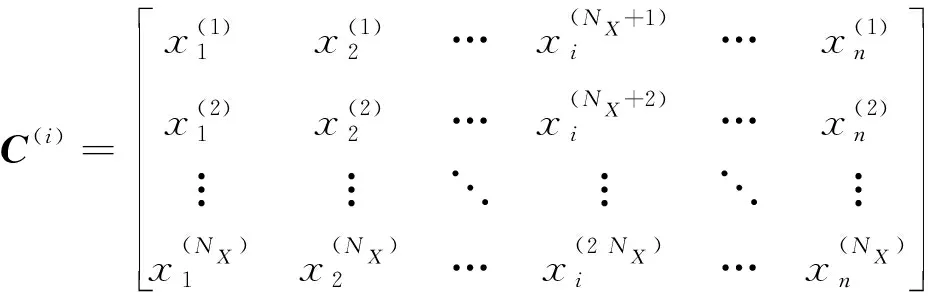
(23)

3) 将矩阵、、()中的样本代入输出模型=()中,获得相应的输出值：

=(),=(),()=(())

(24)

再判断输出值是否落在失效域={:()≤}内,求出相应的指示函数：

F=(),F=(),F()=(())

(25)

4) 通过联合概率密度函数()抽取的分布参数的个样本：

(26)

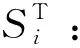
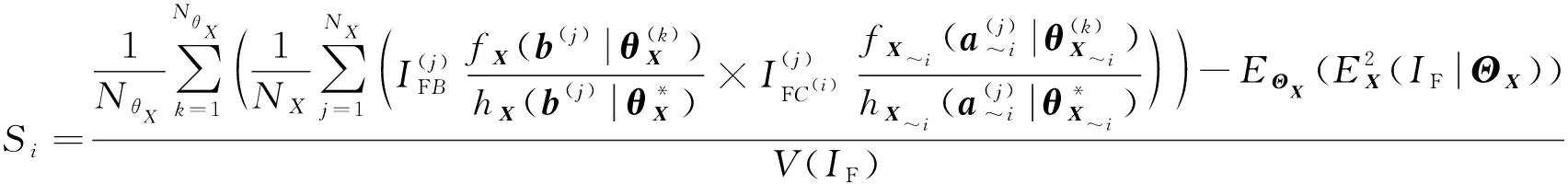
(27)

(28)

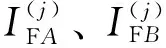
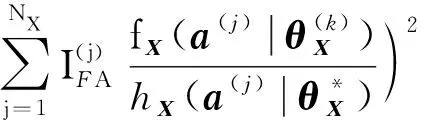
(29)

则

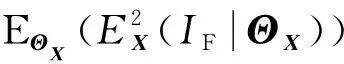
(30)

可以看到尽管式(30)的求解是一个双层嵌套抽样形式,但是就功能函数的使用上而言,只是单层循环计算,总的计算量是(2+)。这和原始的三层循环嵌套抽样的计算量(+)相比要小了很多。

2.2 代理重要抽样法(S-IS)

2.2.1 代理重要抽样密度函数

重要抽样是通过重要抽样概率密度函数()抽取样本的,它的基本思想是：设计点是失效域中对失效概率贡献最大的点,因此选择密度中心在设计点的密度函数作为重要抽样密度函数,可以使得抽取的样本点有较大的概率落在对失效概率贡献较大的区域,从而使得失效概率的估计值较快地收敛于真值。独立标准正态空间中原概率密度函数()与重要抽样密度函数()的等密度线的对比如图1所示。

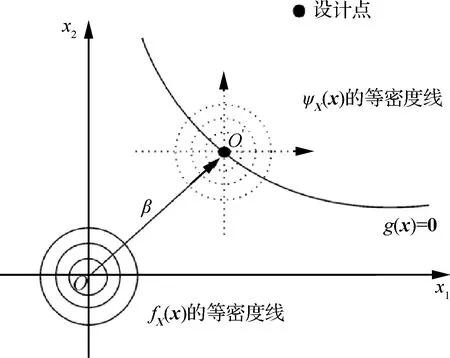
图1 fX(x)与ψX(x)的等密度线对比图[43]Fig.1 Isodensity line comparison diagram of fX(x) and ψX(x)[43]

由一次二阶矩方法或者其他方法得到设计点。

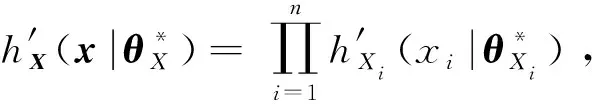
2.2.2 代理重要抽样法

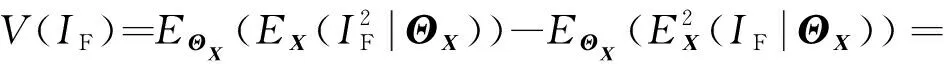
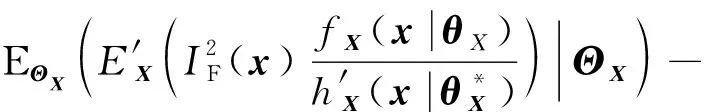
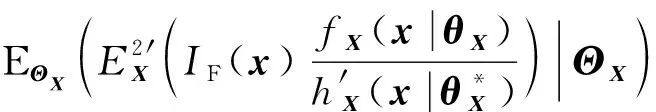
(31)

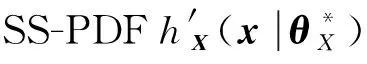
同样,可以得到：

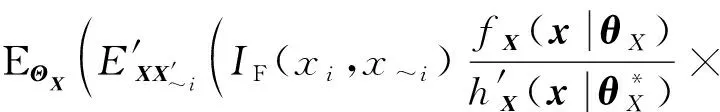
(32)

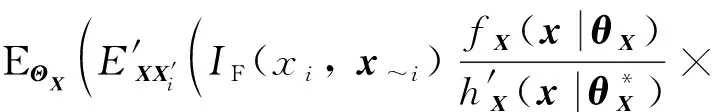
(33)

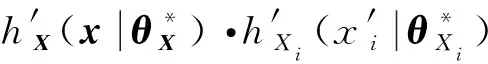
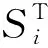
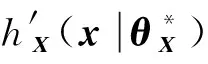
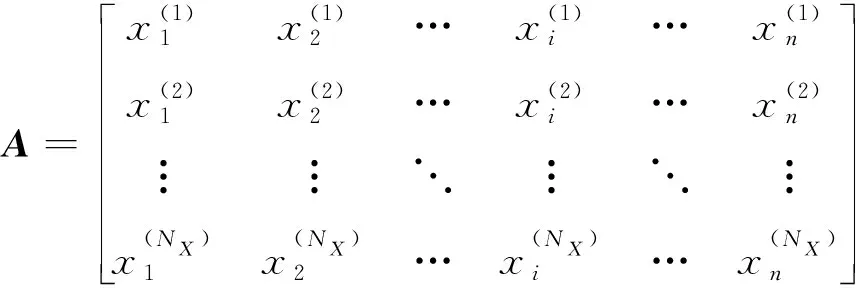
(34)

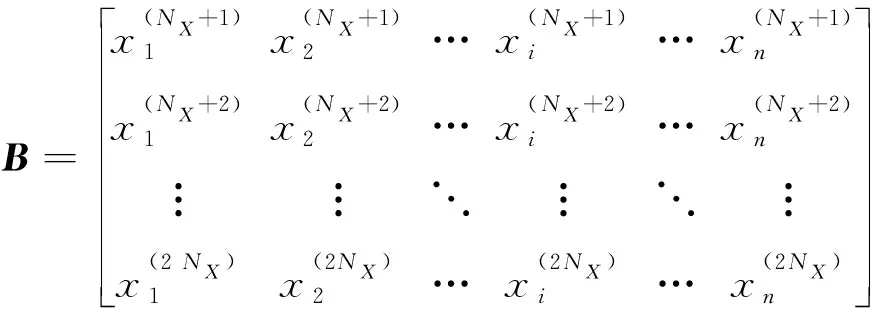
(35)

产生另一个×维样本矩阵(),()中除第外的其他所有列是来自矩阵,第列中的元素是来自于矩阵:

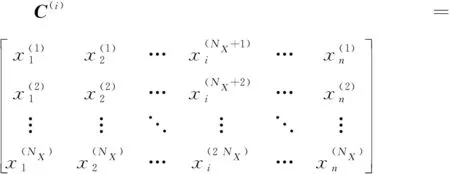
(36)

将矩阵、、()中的样本代入输出模型=()中,获得相应的输出值：

=(),=(),()=(())

(37)

再判断输出值是否落在失效域={:()≤}内,求出相应的指示函数：

F=(),F=(),F()=(())

(38)

通过联合概率密度函数()抽取的分布参数的个样本：

(39)

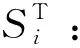
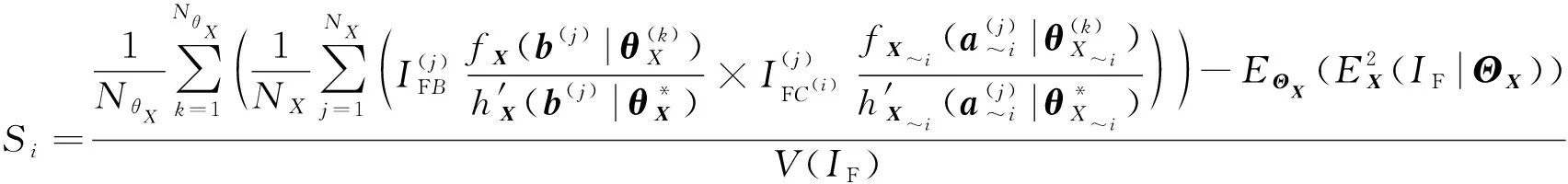
(40)

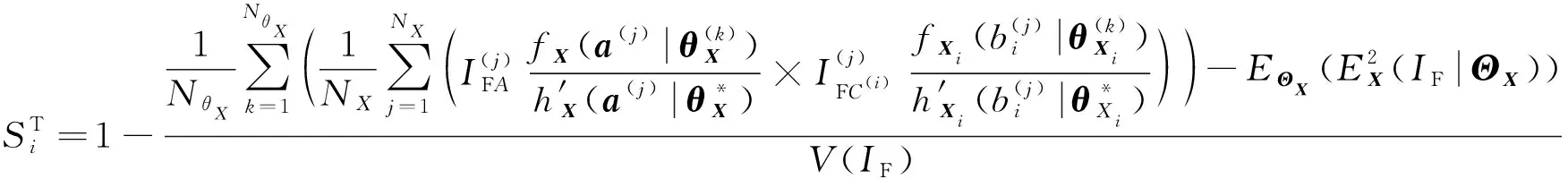
(41)

()通过如式(42)计算：

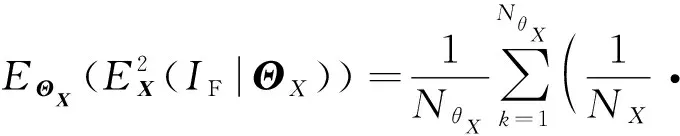
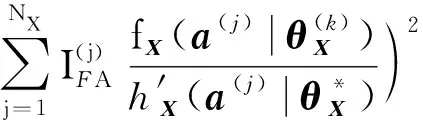
(42)

则

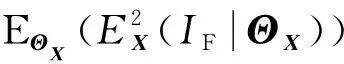
(43)

与代理蒙特卡洛抽样(S-MCS)方法相比,代理重要抽样(S-IS)方法通过将代理抽样密度函数的抽样中心移动到设计点,可以保证产生的大量样本落入失效域内,因此更适合于解决参数不确定性下小失效概率结构系统的可靠性灵敏度分析问题。

2.3 代理截断重要抽样法(S-TIS)

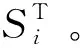
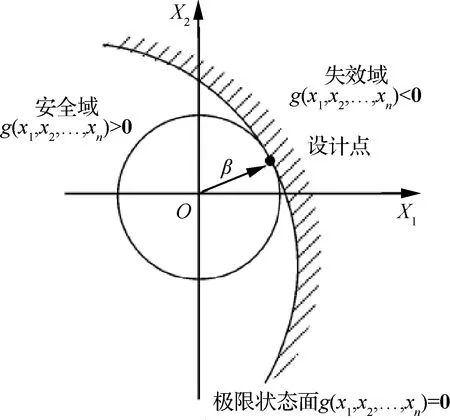
图2 二维情况下β球示意图[43]Fig.2 Schematic diagram of β-sphere in two-dimensional cases[43]

超球内安全样本点功能函数的计算,从而达到在保证计算精度的同时提高可靠性分析效率的目的。

定义超球外区域内的指示函数()为

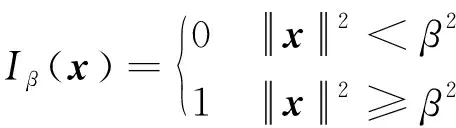
(44)

则式(31)中的无条件方差()转化为

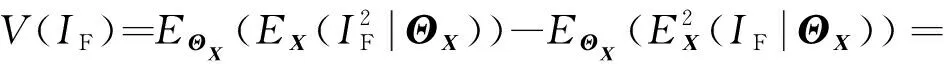
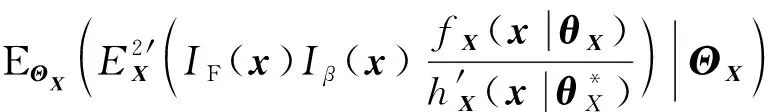
(45)

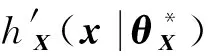
与式(17)推导过程相同,可以得到：

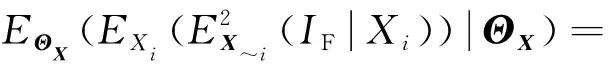
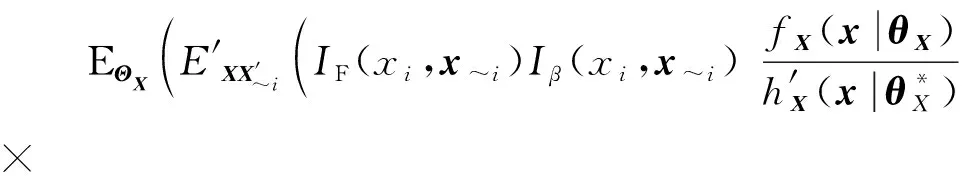
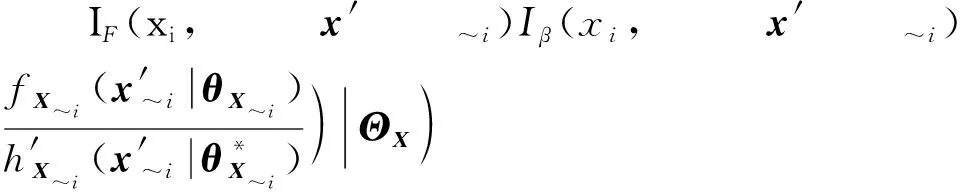
(46)

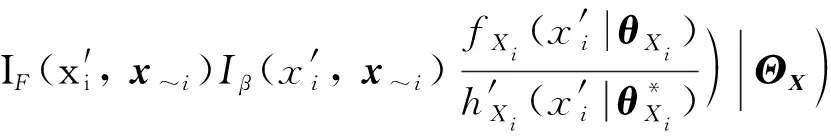
(47)

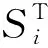
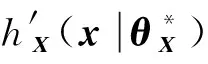
(48)

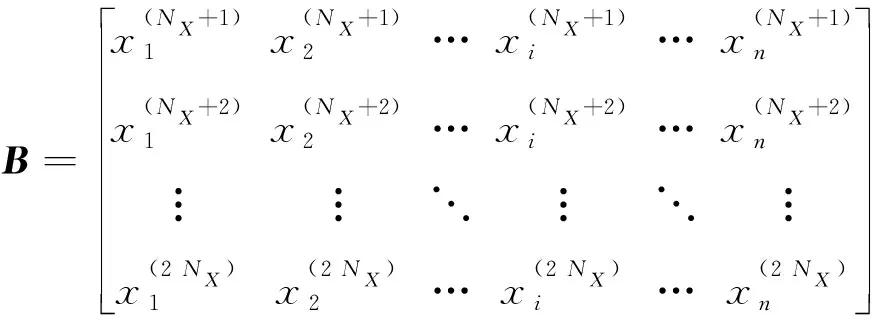
(49)

产生另一个×维样本矩阵(),()中除第外的其他所有列是来自矩阵,第列中的元素是来自于矩阵：

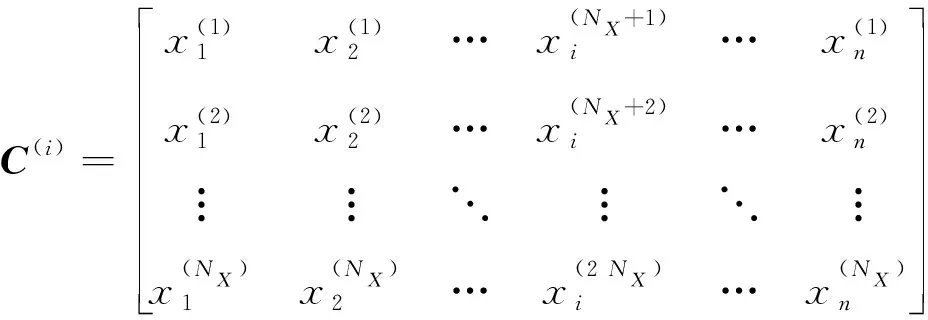
(50)

由式(44)判断、、()中的样本点是否落在球外,求出相应的指示函数：

(51)

将矩阵、、()中筛选出的不为0的样本分别记为′、′、′(),并代入输出模型=()中,获得相应的输出值：

(52)

判断输出值′、′和′()是否落在失效域={:()≤}内,求出相应的指示函数：

(53)

对于矩阵、、()中为0的样本无需代入模型中,直接在失效域指示函数,和中相应行插入0,由此得到完整的失效域指示函数矩阵F、F和F。

通过联合概率密度函数()抽取的分布参数的个样本：

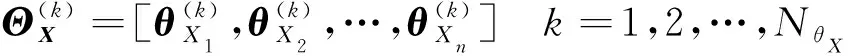
(54)

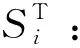
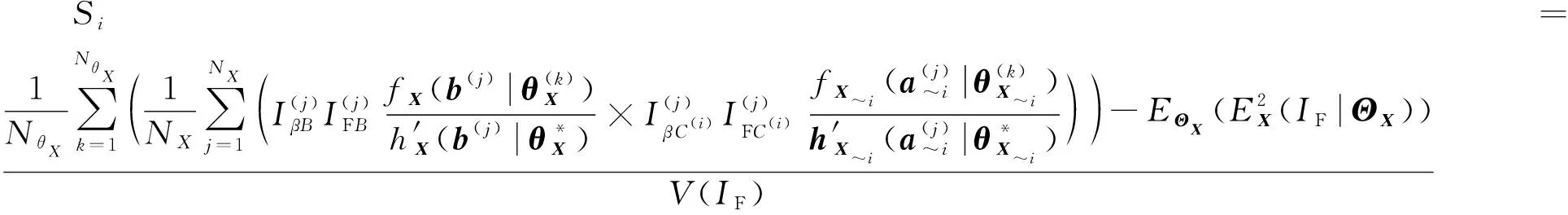
(55)

(56)

()通过式(57)计算：

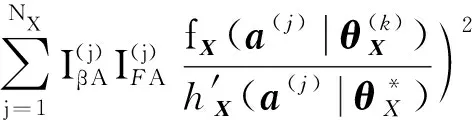
(57)

则

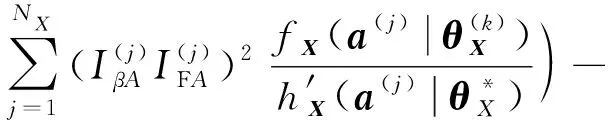
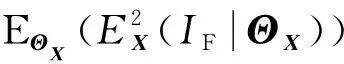
(58)

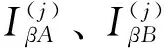
在上述步骤中,不需要计算那些落在球内的样本点的函数值,因此S-TIS方法能在不损失精度的情况下进一步提高S-IS方法参数不确定性下全局可靠性灵敏度分析的效率。

3 算例分析

3.1 数值算例

考虑极限状态函数：

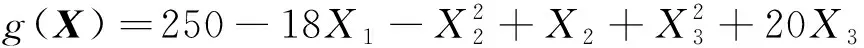
由于算例1中的都服从于正态分布,所以选取的SS-PDF也服从于正态分布。根据SS-PDF的选取原则,算例1中所采用的SS-PDF服从的分布为～(4,45),(=1,2,3)。由AFOSM求解得到的设计点为(912,860,-108),因此S-IS和S-TIS方法采用的SS-PDF为～(912,45),～(860,45),～(-108,45)。

表1给出了用MCS、S-MCS、S-IS、S-TIS这4种方法计算的可靠性灵敏度指标,其中MCS方法为三层嵌套Monte Carlo抽样法,其结果可以作为检验其他方法的参考解。为了方便对比,失效概率同样也列入表中。为各个方法计算和所有变量可靠性灵敏度指标时所需的样本量(确保和的变异系数cov都小于0.1),最后一项模型调用次数是计算过程中调用功能函数计算的总次数。表中估计值后面括号里的数字为其相应的变异系数cov,是通过对可靠性灵敏度指标和失效概率循环计算50次求出的结果。对于三层循环嵌套蒙特卡洛法,给定输入变量数=3,分布参数的样本量=1 000,输入变量的样本量,则模型调用次数为(+)；对于S-MCS方法,模型总的调用次数为(2+)；而对于S-IS,S-TIS方法,设计点迭代优化的次数=28,模型总的调用次数为(2+)+。

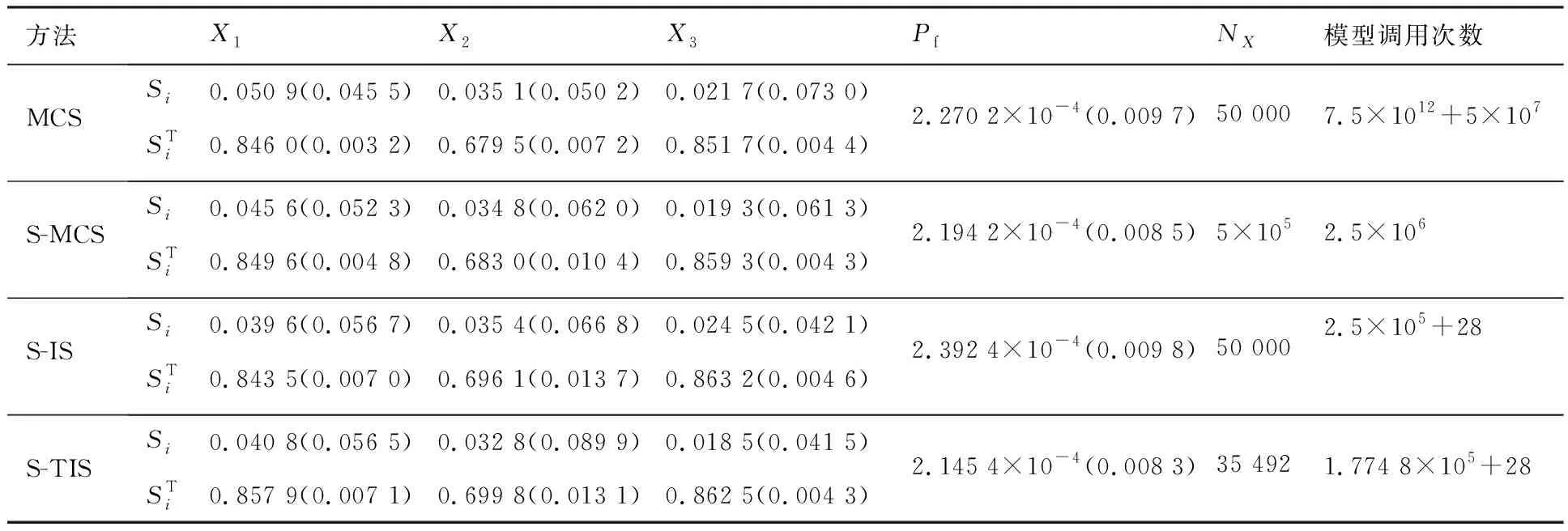
表1 4种方法的可靠性及可靠性灵敏度分析结果

从表1中可以看出,在失效概率比较小的情况下三层嵌套蒙特卡洛法(MCS)所调用的模型次数非常多,耗时很长；而代理抽样蒙特卡洛法(S-MCS)通过把三层抽样转化为单层抽样,大幅度减少了模型调用次数。代理重要抽样法(S-IS)和代理截断重要抽样法(S-TIS)可以进一步以更加少的样本量提供准确的可靠性灵敏度指标。

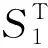
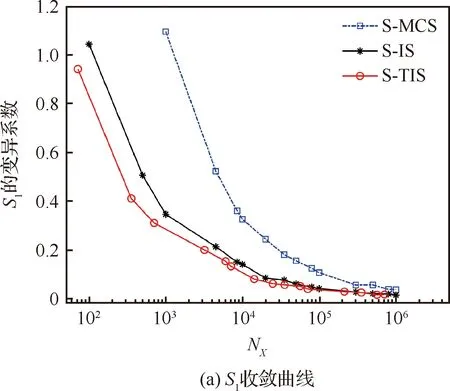
图3 3种方法求解的S1和收敛曲线Fig.3 Convergence curves of S1 and for three methods

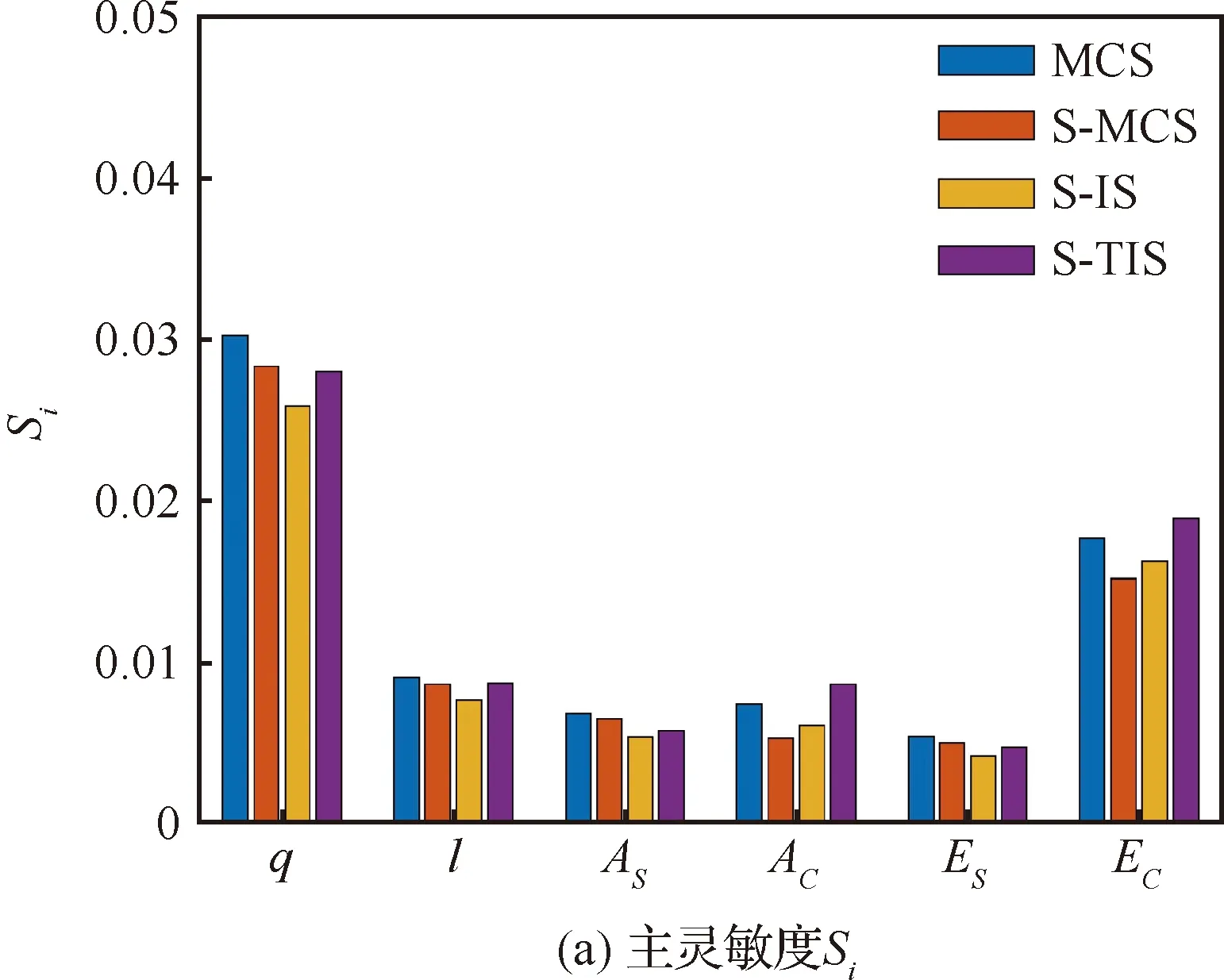
图4 4种方法计算可靠性灵敏度指标对比图(算例1)Fig.4 Comparison diagrams of reliability sensitivity indices for four methods (Case 1)

3.2 工程算例

在航空工程中,钣金零件被广泛使用,最常见的组装方式是铆接。铆接过程中存在着许多影响铆接质量的因素,其中挤压应力是最主要的因素。挤压应力过高可能导致铆接失效。因此,控制铆接过程中的挤压应力对航空部件的安全具有重要意义。

真正的铆接过程非常复杂,本文以无头铆钉为例,将铆接过程简化为图5中的两个阶段。

在阶段Ι,铆钉从状态A(铆接前初始状态,无变形)到状态B(中间状态,铆钉和孔之间无间隙)。在阶段Π,铆钉由状态B到状态C(铆接的最终状态,铆钉头部变形)。整个铆接过程中假设铆钉体积不变。

为了建立挤压应力和铆钉尺寸间的关系,可以假设几个理想条件：

1) 铆接过程中铆钉孔不扩大。

2) 铆钉体积的变化可以忽略。

3) 铆接结束后,铆钉头部为圆柱状。

4) 材料为各项同性。

铆接前,铆钉的初始体积可以表示为

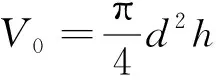
(59)

式中:和为状态A时铆钉的直径和高度。

经过阶段Ι,在状态B时的铆钉体积可以表示为

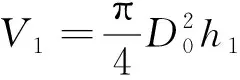
(60)

式中:和为状态B时铆钉的直径和高度。

经过阶段Π,假设铆钉在状态C的上、下部分尺寸相同,则铆钉在状态C的体积可表示为

(61)

式中:为薄壁件的整体厚度;和分别为状态C时铆钉头的直径和高度。

根据硬化强度理论,方向的最大挤压应力可以表示为

=()

(62)

式中:为强度因子;为铆钉材料的硬化因子;为铆钉头在铆接过程中的真实应变。由两部分组成：钉杆的镦粗阶段(阶段Ι)的应变和镦头成形阶段(阶段Π)的应变,所以真实应变可以表示为

=+

(63)

假设铆接过程中铆钉的体积不变,整理式(63) 可得到铆钉的最大挤压应力为

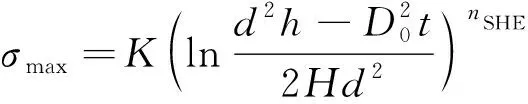
(64)

文中选取铆钉材料为2017—T4,其硬化指数=0.15,镦头高度=2.2 mm。根据材料手册,铆钉的挤压强度为=580 MPa,如果最大挤压应力大于挤压强度,铆钉就会出现失效,因此建立功能函数如下：

=-

(65)

图5 简化的铆接过程Fig.5 Simplified riveting process

在整个铆接过程中,铆钉的尺寸和材料的特性可以认为是正态随机变量,分布参数如表2所示。假设各输入变量的均值也是正态变量,参数如表3所示。

表2 无头铆钉输入变量的分布参数

表3 输入变量均值的分布参数

为了使代理抽样概率密度函数(SS-PDF)覆盖整个输入变量区间,在S-MCS中选定如下SS-PDF：～(5,06),～(20,08),～(51,05),～(5,07)。采用AFOSM求解得到的设计点为,因此S-IS和S-TIS方法中

采用的SS-PDF为～(446,07),～(55046,25)。

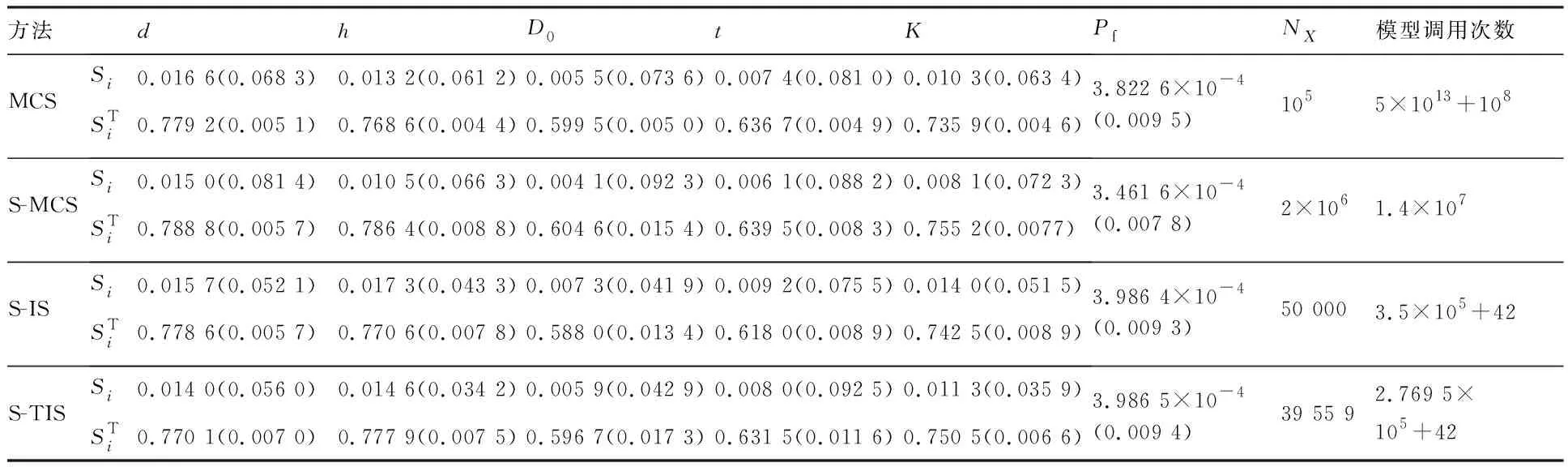
表4 4种方法的可靠性及可靠性灵敏度分析结果(算例2)

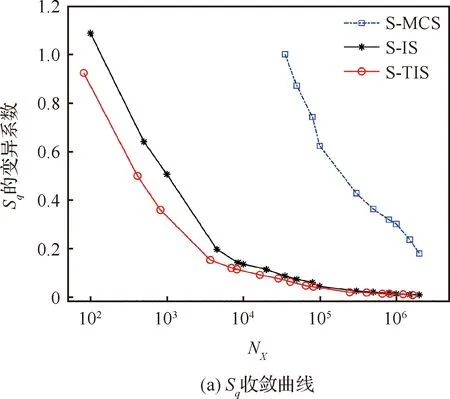
图6 3种方法求解的Sd和的收敛曲线Fig.6 Convergence curves of Sd and for three methods

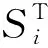
图7 4种方法计算可靠性灵敏度指标对比图(算例2)Fig.7 Comparison diagrams of reliability sensitivity indices for four methods (Case 2)

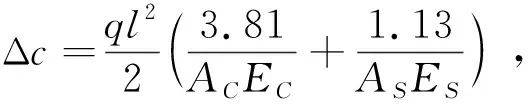
图8 屋架结构示意图Fig.8 A roof truss

表5 屋架结构输入变量的分布参数

表6 输入变量均值的分布参数

为了使代理抽样概率密度函数覆盖整个输入变量区间,选定如下SS-PDF：～(20 000,1 100),～(12,032),～(982×10,(70×10)),～(004,0006),～(12×10,(462×10)),～(3×10, (3.52×10))。用AFOSM求解得到设计点

为(213 49,124,888×10,0032 4,1169×10,268×10),因此S-IS和S-TIS方法中采用的SS-PDF为～(21 349,1 100), ～(124,032),～(888×10,(70×10)),～(0032 4,0006)～(1169×10,(462×10))～(268×10,(352×10))。

表7 4种方法的可靠性及可靠性灵敏度分析结果(算例3)Table 7 Reliability and reliability sensitivity analysis results of four methods (Case 3)

4 结 论

1) 本文主要研究了参数不确定性下高效的可靠性灵敏度的分析方法。首先定义了参数不确定性下输入变量基于可靠性的主灵敏度指标以及总灵敏度指标,以衡量输入变量的不确定性在整个参数空间中对失效概率的平均影响。然后,借鉴已有单层抽样的思想,通过引入代理抽样概率密度函数将参数不确定性下可靠性灵敏度指标直接求解中的三层抽样转化为单层抽样,大大减少了参数不确定情况下可靠性灵敏度指标分析的计算量。并针对小失效概率可靠性问题,进一步优化代理抽样密度函数,并结合IS以及TIS思想,提出了更加高效的S-IS以及S-TIS方法。

2) 本文算例结果表明,和标准的三层循环嵌套抽样蒙特卡洛法相比,S-MCS方法能不依赖于输入变量及其参数的分布,以较少的计算量提供准确的可靠性灵敏度指标,S-IS以及S-TIS方法通过将代理抽样密度函数的抽样中心移动到设计点,保证产生的大量样本落入失效域内,减少计算灵敏度指标所需抽取的样本量,S-TIS方法更是通过去掉超球内的样本点进一步减少了计算量。另外,各算例的结果表明,变量单独作用对失效概率产生的影响可以忽略不计,这可能因为对于小失效概率结构系统,落入失效域内的样本点较少,导致变量对失效概率的单独作用影响也十分的小。

3) 在本文的S-IS以及S-TIS方法中,设计点是通过AFOSM数值计算得到的,对于高维问题来说其计算结果可能并不准确,这会在一定程度上影响方法的效率和精度。为了解决这一问题,可以采用模拟退火、马尔科夫链、遗传算法等方法进行设计点的优化选取,使得可靠性灵敏度的计算更加可靠。