基于无偏灰色-马尔科夫链模型的北京市水资源需求预测研究

蔡剑英，王 烜*，蔡宴朋

（1.北京师范大学 环境学院 水环境模拟国家重点实验室，北京 100875；2.北京师范大学 环境学院 水沙科学教育部重点实验室，北京 100875；3.广东工业大学 环境生态工程研究院/广东省流域水环境治理与水生态修复重点实验室，广州 510006）

水资源是人类生存和发展不可或缺的物质基础，也是社会经济可持续发展的重要资源[1]。伴随着经济社会发展和人口快速增长，人类对水资源的需求量日益增多，水资源供需矛盾日趋尖锐[2]。在许多城市，缺水问题已经成为制约区域经济发展和生活水平提高的重要因素[3]。需水预测作为水资源规划管理工作的前提，对水资源的合理调配具有指导作用。因此，围绕变化环境下的区域需水量开展预测研究是促进社会经济可持续发展和水资源高效利用的必然要求[4]。

目前，需水量预测的研究方法主要包括时间序列法、结构分析法和系统分析法等[5-6]。时间序列法是依据区域水资源的历史统计数据，找到其随时间变化的规律，建立对应的时序模型，进而推测需水量的未来数值，大致可分为滑动平均法、趋势外推法、季节变动法、马尔科夫法等。苏思沁[7]结合小波分析与时间序列方法，预测了西安市的短期城市需水量，并提出了水资源可持续利用的合理建议。该方法虽然应用方便，但是需要建立在大量长时间数据样本的基础上，存在预测周期短的缺点，不适合中长期预测[8]。结构分析法以影响事物本身及发展的因素及相关关系为出发点，构建水资源与影响因素之间相互关系的预测模型，通过分析影响因素的变化规律间接反映水资源的变化规律，主要有回归分析法、用水弹性系数法与定额法等。李艳萍[9]运用逐步回归和通径分析方法，分析玉溪市用水量及其影响因素，构建了用水量预测模型，结果表明该模型能较好拟合玉溪市的用水量变化。该方法的主要缺点是选取影响因素时存在较多人为的不确定性因素，会对预测结果造成偏差。系统分析法采用系统科学的观点，基于对需水系统结构的研究，构建对应的水资源需求系统模型，实现对未来需水量的预测研究，主要包括灰色方法、无偏灰色方法、人工神经网络法和系统动力学模型等。Li等[10]采用系统动力学模型模拟了2015—2030年深圳市的水资源供需状况，结果表明所构建模型在预测方面表现出良好的性能。

虽然上述研究方法能较为简便地计算出未来规划年的区域需水量预测结果，但最终得到的是确定的预测数值，属于点预测结果，会导致不同程度的误差存在，影响水资源的科学配置[11]。此外，由于水资源需求受到气候变化、经济社会与管理政策等多方面的影响（如人口数量、经济规模、降雨过程的随机分布等不确定性因素），使其呈现出随机性、波动性较大的特点，对预测结果产生不确定性影响，给水资源的调度决策工作带来一定程度的风险[12]。因此，亟须采用不确定性分析方法来处理和表征一定时期内水资源需求量随机波动的影响程度。

在众多的预测方法中，无偏灰色模型算法操作简单，预测精度高，当时间序列波动较大时，其拟合精度会大大降低。而马尔科夫链模型能根据相关状态间的转移概率来反映多个随机因素的影响程度，其研究对象通常具有随机变化的特点，对波动性数据具有较高的相容性，很好地克服了无偏灰色模型的缺点，实现了对预测数据的误差修正[13]。最终得到的需水量预测结果将以区间值进行表述，包含下限值和上限值，将不确定性界定在一个区间范围内，有效表征需水量随机波动的不确定性信息，解决了水资源系统中的不确定性问题[14]。因此，本研究以北京市为例，耦合无偏灰色与马尔科夫链模型，预测未来规划年的需水量区间范围，量化水资源系统的不确定性信息，提高需水量预测结果的准确性，对制定科学的水资源管理决策，实现水资源的科学配置具有重要的指导意义。

1 研究区概况

北京是我国的首都，也是全国的政治、文化、科技创新和国际交往中心。它位于东经115.70°～117.40°，北纬39.40°～41.60°，总面积达16 410.54 km2，下辖海淀、朝阳和西城等16个行政区（图1）。北京市属于暖温带半湿润半干旱季风气候，夏季高温多雨，冬季寒冷干燥，降水季节分配不均匀。

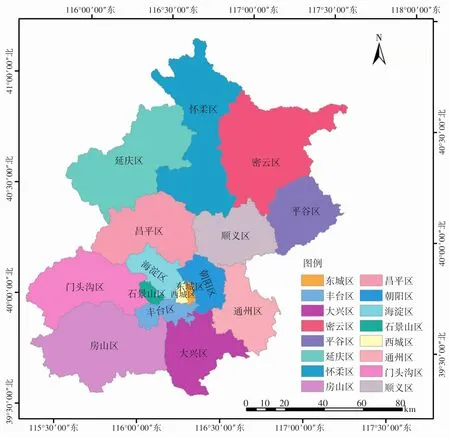
图1 北京市行政区示意图Fig.1 The district map of Beijing City

北京市属于资源型严重缺水地区，人均水资源量远低于国际公认严重缺水标准[15]。北京市的多年平均水资源量为2.48×109m3，但用水总量高达 3.54×109m3，缺口达 1.06×109m3，主要依靠地下水超采和从周边省份调水来弥补。近年来，南水北调来水正逐渐成为北京市的重要供水水源。2018年，南水北调中线工程向北京市供应9.30×108m3水量，占总供水量的24%。北京市的用水包括农业、工业、生活和生态用水。2018年，北京市生活用水1.84×109m3，占总用水量的47%；生态用水1.34×109m3，占比34%；农业部门用水0.42×109m3，占比11%；工业部门的用水比重最少，仅为8%。水资源的优化配置是缓解区域水资源短缺的重要手段，而区域需水量预测是水资源调度决策和可持续管理的重要依据[16]，因此，提高需水量预测结果的准确性对于水资源的合理配置和高效利用具有重要意义。

2 数据来源与研究方法

2.1 数据来源

本研究以北京市的行政区域边界为系统空间研究边界，模型的时间边界为2001—2030年，其中2001—2014年为历史统计数据年，2015—2020年为模型验证年，2021—2030年为模型预测年，时间间隔为1年。2001—2020年的北京市农业、工业、生活和生态需水量等基础数据主要来源于《北京统计年鉴》和《北京市水资源公报》（2001—2020）等。

本研究首先利用2001—2014年的需水量数据进行无偏灰色模型的参数率定，采用2015—2020年北京市的水资源需求数据进行验证，分析无偏灰色模型的精度；接着采用马尔科夫链模型对需水量模拟值进行修正，并比较经马尔科夫链模型修正前后的需水量模拟结果，评价其改进精度；最后利用无偏灰色-马尔科夫链模型对需水量进行模拟预测，得到北京市2021—2030年的需水量区间预测结果，为北京市水资源的优化配置和高效利用提供支持。

2.2 研究方法

2.2.1 无偏灰色模型

灰色预测模型由邓聚龙教授[17]于1982年提出，其基本原理：当预测数据列是一个变量时，一阶微分方程GM（1，1）模型将原始数据列按照时间累计相加后得到新的时间序列数据，通过求解一阶线性微分方程可以无限逼近该新时间序列数据。该方法的优点是所需信息量较少，计算方便快捷，精确度较高[18]。然而，灰色GM（1，1）模型基于指数型曲线，不满足协调条件，累加建模过程中舍弃原始序列的第一点，预测结果与实际值存在一定的偏差，因此，许多专家学者对灰色理论进行不断探索与改进[19-20]。其中，穆勇[21]提出的无偏灰色模型是在保留灰色预测的核心理论前提下，通过优化灰导数白化值，建立具有白指数律重合性的模型，简化了建模步骤，提高了模型精度，也扩大了灰色模型的适用范围，在水资源需求预测领域得到了广泛应用。

无偏灰色模型首先对原始时间序列数据做一次累加，得到一组新的时间数列，进而建立一阶线性微分方程模型，利用线性微分方程求得拟合曲线，从而对水资源需求进行预测。具体过程[22]如下：

设水资源需求量的时间序列数据：

式中：x（0）为原始时间数据序列；n为样本的长度。

对x（0）做一次累加生成序列：

对x（1）建立一阶灰色微分及白化方程可以表示为：

式中：a、b为基于最小二乘法得到的方程系数：z(1)k为灰导数背景值，通常由1/2[x(1)(k)+x(1)(k-1)]等式得到。最小二乘估计系数a与b的计算公式如下：

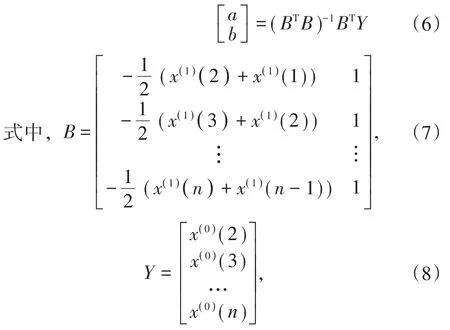
得到无偏灰色模型的相关系数可表示为：

因此，处于k时期的序列值可通过以下公式求得：

无偏灰色模型的有效性检验一般采用相对误差e（k）及平均绝对百分误差值（MAPE），判断预测结果的准确性。e（k）和MAPE的计算公式为：

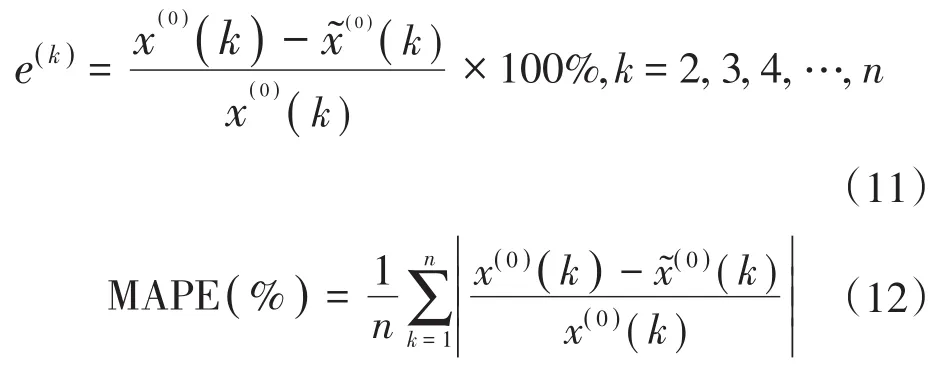
通常来说，若对所有的i有MAPE＜10%，则认为模型达到较高要求。若对所有的i有MAPE＜20%，则认为模型达到一般要求[23]。

2.2.2 马尔科夫链模型

马尔科夫的概念由安德雷·马尔科夫在19世纪末期提出[24]。马尔科夫链模型的基本原理是基于马尔科夫链和事件的现状，预测将来各时期的变化情况。在随机过程中，有一类具有“无后效性”的性质，即随机过程在t（t＞t0）时刻所处的状态仅与t0时刻相关，而与t0时刻前的状态无关，该特性称为“马尔科夫性或无后效性”，具有此性质的过程称为马尔科夫过程。时间和状态都离散的马尔科夫过程，称为马尔科夫链，其被广泛应用于随机模型的构建以预测未来时间的发生及其可能性[25]。马尔科夫链与无偏灰色模型的耦合和建模步骤[4，26]如下：

1）划分状态。将无偏灰色模型中预测数据相对于原始数据的相对误差定义为状态H，并划分成n个状态，则任一个状态区间Hi=[Hi1，Hi2]，i=1,2，…，n。其中Hi1和Hi2分别为区间的下限和上限。

3）确定状态转移的概率准则。设系统初始时刻处于状态Hi，初始状态向量β(0)=[β1(0)，β2(0)，…，βn(0)]，经一步从初始状态Hi转移到下一状态Hj的概率为，而βj=max[β1(1),β2(1)，…,βn(1)]，当系统经k步从初始状态Hi转移到状态Hs，，而βs(k)=max[β(0)Pk]=max[β1(k)，β2(k)，…，βn(k)]。

3 结果分析

3.1 基于无偏灰色模型的北京市需水量预测

分别以北京市2001—2014年的农业、工业、生活和生态需水量数据和2004—2014年的生态需水量为原始数据，进行无偏灰色模型的参数率定，得到北京市2001—2014年农业、工业、生活和生态需水量的模拟结果（表1）。结果表明，北京市的农业、工业、生活和生态需水量实际值与无偏灰色预测值的MAPE值分别为3.81%，6.33%，2.04%和8.29%，均低于10%，表明无偏灰色模型达到较高要求，模拟精度良好，能较好地模拟北京市的农业、工业、生活和生态需水量。

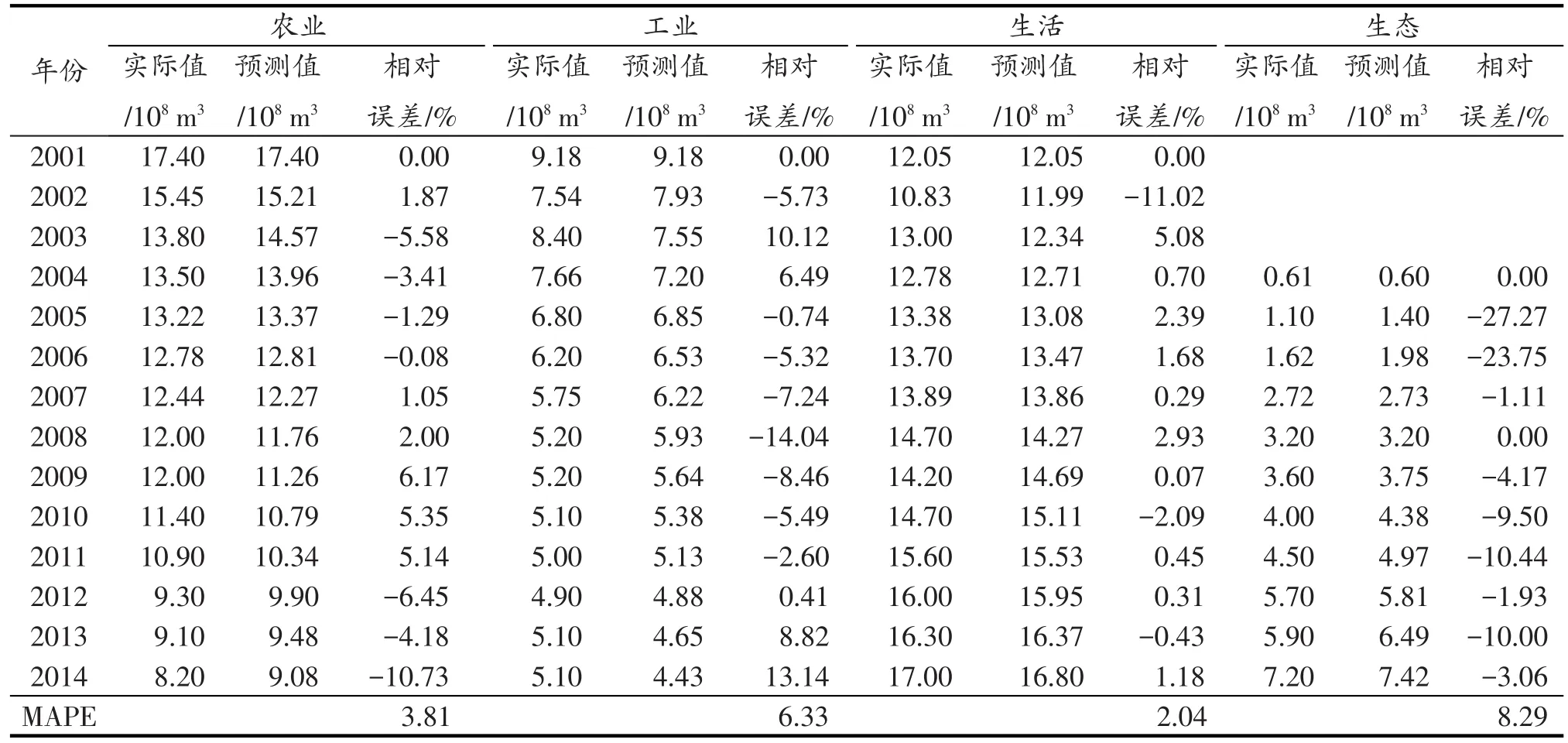
表1 北京市2001—2014年的需水量实际值与无偏灰色预测值比较Table 1 Comparison of actual water demands and predicted water demands using unbiased grey in Beijing City from 2001 to 2014

参数率定后，再采用无偏灰色模型模拟北京市2015—2020年的农业、工业、生活和生态需水量，将预测结果与实际值进行比较，验证无偏灰色模型的精度，结果见表2。可以发现，北京市2015—2020年的农业、工业、生活和生态需水量预测值与实际的MAPE值分别为8.25%，5.82%，3.59%和6.61%，表明无偏灰色模型达到较高要求，再次验证了无偏灰色模型良好的模拟精度，并最终得到基于无偏灰色模型的北京市2021—2030年的需水量预测结果（表3）。根据本文的预测结果，北京市2020年和2030年的总需水量分别为4.30×109m3和5.023×109m3。秦欢欢[27]利用系统动力学模型，依据北京市当前的发展模式，预测北京市2020和2030年的水资源需求量分别为4.59×109m3和4.91×109m3，与本研究的预测结果基本接近，进一步验证了本研究结果的可靠性。

表2 北京市2015—2020年需水量实际值与无偏灰色预测值比较Table 2 Comparison of actual water demands and predicted water demansd using unbiased grey model in Beijing City from 2015to2020

表3 基于无偏灰色模型的北京市2021—2030年需水量预测结果Table 3 Prediction results of water demands in Beijing City from 2021 to 2030 based on unbiased grey model（单位：108m3）

3.2 基于无偏灰色-马尔科夫链模型的北京市需水量预测

根据2001—2014年基于无偏灰色模型的北京市需水量预测结果的相对误差，将农业、工业、生活和生态需水量的相对误差值划分为4个状态区间，其中：农业需水量的状态区间分别为：[-11%，-5%]，（-5%，0%]，（0%，5%]和 （5%，10%]；工业需水量的状态区间分别为：[-15%,-7%]，（-7%，0%]，（0%，7%]和（7%，15%]；生活需水量的状态区间分别为：[-12%，-6%]，（-6%，0%]，（0%，5%]和（5%，10%]；生态需水量的状态区间分别为：[-30%，-22.5%]，（-22.5%，-15%]，（-15%，-7.5%]和（-7.5%，0%]。结合相对误差的转移状态，确定农业、工业、生活和生态需水量的一步概率转移矩阵[23，28-29]：

根据一步状态转移概率矩阵，基于无偏灰色预测值，利用马尔科夫链模型，最终得到修正后的北京市2021—2030年的农业、工业、生活和生态需水量预测值，结果见表4。可以看出，修正后的北京市需水量预测结果以区间值进行表述，将需水量随机波动的不确定性信息界定在一个区间范围内，有效量化了需水预测系统的不确定性信息。

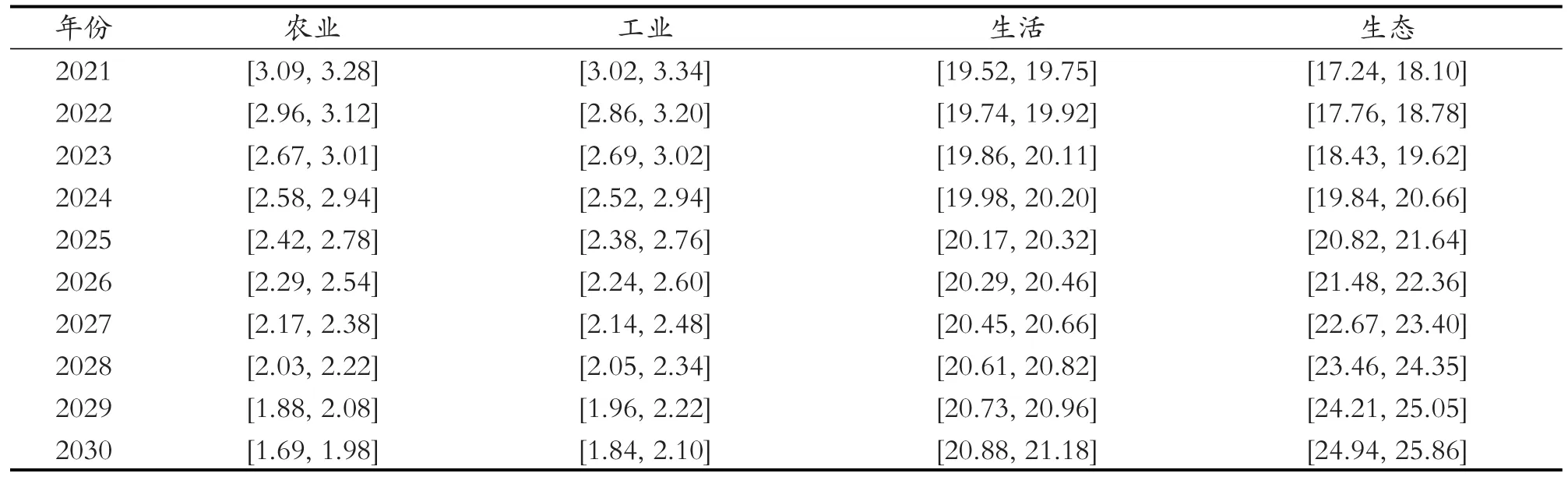
表4 基于无偏灰色-马尔科夫链模型的北京市2021—2030年需水量预测结果Table 4 Interval prediction results of water demands in Beijing City from 2021 to 2030 based on unbiased grey Markov chain model（单位：108m3）

4 讨论

4.1 马尔科夫链模型的改进精度评价

本文采用区间预测结果的中间值进行分析[22，23，28，30]，对比北京市需水量实际值与无偏灰色-马尔科夫链预测值之间的相对误差。以北京市农业需水量模拟结果为例（表5），可以发现：北京市农业需水量实际值与马尔科夫链模型修正后预测值的MAPE值为1.68%，表明模拟精度很高。同时，对比无偏灰色预测值与无偏灰色-马尔科夫链预测值之间的相对误差，可知：经过马尔科夫链模型修正后的农业需水量MAPE值显著降低，从3.81%降到1.68%。类似地，通过计算得到北京市工业、生活和生态需水量实际值与马尔科夫链模型修正后预测结果的MAPE值分别为3.65%、1.77%和3.07%，均达到高精度。相比于无偏灰色模型，修正后的工业、生活和生态需水量MAPE值也显著降低，模型精度得到提高。这是由于马尔科夫链模型适合处理波动性较大的随机性数据，具有较强的抗干扰性，能有效量化水资源需求系统的不确定性因素，因此，修正后的需水量预测精度明显提高，这与李义华等[28]和龚明等[29]对马尔科夫链模型的改进精度结论基本吻合。

表5 北京市农业需水量实际值与无偏灰色、无偏灰色-马尔科夫链预测值的比较结果Table 5 Comparison of actual agricultural water demand and predicted agricaltural water demands using unbiased grey,unbiased grey-Markov chain prediction results in Beijing City

绘制北京市农业、工业、生活和生态需水量的实际值与无偏灰色、无偏灰色-马尔科夫链预测值的比较结果（图2）。可以看出，经过马尔科夫链模型修正后的需水量预测值与实际值更贴合，进一步验证了马尔科夫链模型的有效性和改进精度。

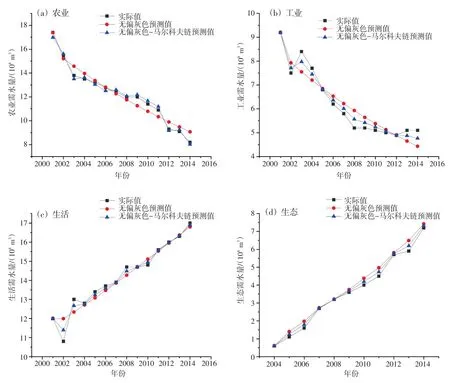
图2 北京市需水量实际值、无偏灰色与无偏灰色-马尔科夫链预测值的比较结果Fig.2 Comparison of actual water demands and predicted water demands using unbiased grey,unbiased grey-Markov chain in Beijing City

4.2 区间预测结果在水资源优化配置中的应用

通过无偏灰色-马尔科夫链模型，本文得到北京市需水量区间预测结果，表现为包含下限和上限值的区间范围。通过将需水量随机波动的影响程度界定在一个包含精确结果的区间范围内，区间分析方法有效量化了需水系统受人口、经济和政策规划等不确定性因素的影响，考虑了更多的计算误差，与点预测结果相比，更具有实际意义[31]。

区间预测结果更有利于水资源的优化配置和可持续利用。基于区间的区域需水量预测结果，能为决策者的水资源规划管理提供操作余地和空间，帮助决策者结合区域实际情况，更科学地对水资源进行调度决策，实现社会、经济和生态环境效益的最大化。从水资源供需平衡理念出发，当水资源供给量受到限制，如枯水年时，决策者可根据区间预测结果的下限值，在保障农业、工业、生活和生态的最低需水量前提下，注重节水优先，不断提升管水方式和用水效能；当水资源供给量较为充足，如丰水年或平水年时，决策者可结合区间预测结果的下限和上限值，一方面保障区域的最低需水量，另一方面不断提高公民的节水意识，确保用水量不超过最高需水量。

根据《北京市“十三五”时期水务发展规划》，2020年全市年用水总量计划增加至4.30×109m3，而北京市2020年实际用水量为4.06×109m3，体现了北京市在节水型社会的构建方面已经卓有成效。南水北调中线通水后，虽然有效缓解了北京市地下水超采趋势和水资源紧张状况，但人均水资源量仍远低于国际公认的极度缺水标准，水资源“紧平衡”状态仍未得到根本改变。按照《北京城市总体规划（2016—2035年）》，北京要建设水城共融的生态城市，到2035年人均水资源量提高到220 m3，全面建设节水型社会。因此，北京市应该坚持“开源”和“节流”齐头并进，在保障城市最低需水量的前提下，不断完善外调水、本地地表水、地下水、再生水和雨洪水五水共济的水源保障和供水体系，同时要坚持节水优先，严格控制用水总量，调整用水结构，确保不超过最大需水量，保障首都水资源的高效利用，提高水安全保障能力，促进水与城市协调发展。

4.3 无偏灰色-马尔科夫链模型的改进空间

本文结果表明，无偏灰色-马尔科夫链模型在需水预测研究方面具有优势，王冰[4]、熊祖强等[22]和张茜等[25]的研究结果同样也验证了该模型在需求预测方面的模拟精度。但是无偏灰色-马尔科夫链模型仍存在一些缺陷，主要包括：

（1）当需求量的历史数据波动性较大时，模型预测精度会降低。针对这一不足，可尝试通过扩大样本容量，或者对历史数据进行筛选和处理，一定程度上能提高预测结果的精度。

（2）无偏灰色-马尔科夫链模型虽然实现了对需求量数据的修正，预测结果以区间范围进行表述，有效处理了需水系统中的不确定性问题。但是无偏灰色-马尔科夫链模型修正的是一个经过气候变化、人为活动和社会经济等外界因素综合作用的确定数值，无法通过改变模型参数，制订不同的情景方案，进而模拟区域需水量的动态变化。针对这一问题，可通过组合不同的预测方法，如神经网络和系统动力学[32]等方法，不断提高模拟结果与实际情况的拟合度。如景亚平等[33]耦合了灰色、BP神经网络和马尔科夫链模型，模拟预测榆林市的用水量，结果表明，组合后的需水量预测模型的精度显著提高。

5 结论

区域需水量预测研究是城市水资源规划管理和优化调配的重要基础。本文通过构建无偏灰色-马尔科夫链模型，基于北京市2001—2020年的需水量数据进行参数率定和验证，得到2021—2030年的水资源需求量预测结果。结果表明：（1）无偏灰色-马尔科夫链模型模拟精度良好，能较好地模拟北京市的农业、工业、生活和生态需水量；（2）马尔科夫链模型具有较好的抗干扰性，适合处理波动性较大的随机性数据，修正后的需水量预测精度显著提高；（3）需水量预测结果以区间值表述，将不确定性界定在一个区间范围内，有效表征了需水预测系统的不确定性信息；（4）为了保障生态系统的稳定和社会经济的可持续发展，北京市不仅要注重水资源的优化配置和统筹兼顾，更要注重节水优先，严格控制用水总量，推进节水型社会的建设。上述研究结果可为区域水资源的综合规划与管理提供参考和技术支持。